文章目录
- [一 古典密码体制](#一 古典密码体制)
-
- [1.1 置换加密体制](#1.1 置换加密体制)
- [1.2 代换加密体系](#1.2 代换加密体系)
- [1.3 单表代换密码](#1.3 单表代换密码)
- [1.4 多表代换密码](#1.4 多表代换密码)
- [1.5 典型的多表代换密码算法](#1.5 典型的多表代换密码算法)
- [1.6 多表代换密码的统计分析](#1.6 多表代换密码的统计分析)
- [二 现代密码学的三条原则](#二 现代密码学的三条原则)
一 古典密码体制
- 古典密码体制(传统密码体制或经典密码体制)主要通过字符间的置换和代换来实现。
- 古典加密方案主要有两种主要方法------置换密码和代换密码。代换密码,包括单表加密和多表加密。
- 唯密文攻击,如单表代换的统计(频率)分析攻击方法和多表代换加密的统计分析攻击方法。
1.1 置换加密体制
-
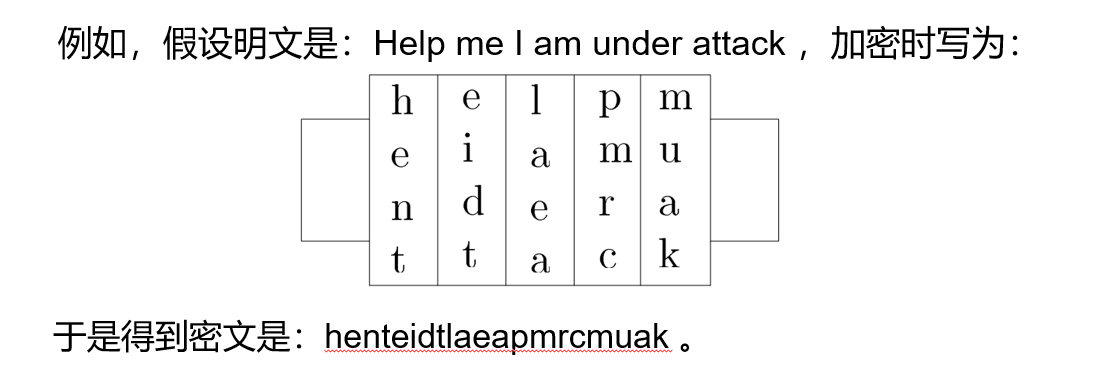
置换密码(Permutation Cipher)/换位密码(Transposition Cipher)指根据一定的规则重新排列明文。密文空间和明文空间相同,故密文只是打乱了明文字符的位置和次序 。如Scytale密码:
-
定义:设 S 是一个有限集合, φ φ φ 是从 S S S 到 S S S 的一个映射,如果对任意 u , v ∈ S u, v ∈ S u,v∈S,当 u ≠ v u ≠ v u=v 时, φ ( u ) ≠ φ ( v ) φ(u) ≠ φ(v) φ(u)=φ(v),则称 φ φ φ为 S S S上的一个置换(Permutation)。
-
设 n n n 为一固定整数, P 、 C P、C P、C 和 K K K 分别为明文空间、密文空间和密钥空间。明/密文是长度为 n n n 的字符序列,分别记为
X = < x 1 , x 2 , ... , x n > ∈ P X = <x_1, x_2, \ldots, x_n> \in P X=<x1,x2,...,xn>∈P, Y = < y 1 , y 2 , ... , y n > ∈ C Y = <y_1, y_2, \ldots, y_n> \in C Y=<y1,y2,...,yn>∈C, K K K 是定义在 { 1 , 2 , ... , n } \{1, 2, \ldots, n\} {1,2,...,n} 的所有置换的集合。对任何一个密钥 σ ∈ K \sigma \in K σ∈K(即一个置换),定义置换加密如下:
e σ ( x 1 , x 2 , ... , x n ) = ( x σ ( 1 ) , x σ ( 2 ) , ... , x σ ( n ) ) e_\sigma(x_1, x_2, \ldots, x_n) = (x_{\sigma(1)}, x_{\sigma(2)}, \ldots, x_{\sigma(n)}) eσ(x1,x2,...,xn)=(xσ(1),xσ(2),...,xσ(n))
d σ − 1 ( y 1 , y 2 , ... , y n ) = ( y σ − 1 ( 1 ) , y σ − 1 ( 2 ) , ... , y σ − 1 ( n ) ) d_{\sigma^{-1}}(y_1, y_2, \ldots, y_n) = (y_{\sigma^{-1}(1)}, y_{\sigma^{-1}(2)}, \ldots, y_{\sigma^{-1}(n)}) dσ−1(y1,y2,...,yn)=(yσ−1(1),yσ−1(2),...,yσ−1(n))这里 σ − 1 \sigma^{-1} σ−1 是 σ \sigma σ 的逆置换,密钥空间 K K K 的大小为 n ! n! n!。
-
设有限集 X = { 1 , 2 , 3 , 4 , 5 , 6 , 7 } X = \{1, 2, 3, 4, 5, 6, 7\} X={1,2,3,4,5,6,7}, σ \sigma σ 为 X X X 上的置换,有 σ ( 1 ) = 3 \sigma(1) = 3 σ(1)=3, σ ( 2 ) = 1 \sigma(2) = 1 σ(2)=1, σ ( 3 ) = 5 \sigma(3) = 5 σ(3)=5, σ ( 4 ) = 2 \sigma(4) = 2 σ(4)=2, σ ( 5 ) = 4 \sigma(5) = 4 σ(5)=4, σ ( 6 ) = 7 \sigma(6) = 7 σ(6)=7, σ ( 7 ) = 6 \sigma(7) = 6 σ(7)=6。可直观表示为:
σ = [ 1 2 3 4 5 6 7 3 1 5 2 4 7 6 ] \sigma = \begin{bmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 3 & 1 & 5 & 2 & 4 & 7 & 6 \end{bmatrix} σ=[13213542546776]
σ − 1 = [ 1 2 3 4 5 6 7 2 4 1 5 3 7 6 ] \sigma^{-1} = \begin{bmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 2 & 4 & 1 & 5 & 3 & 7 & 6 \end{bmatrix} σ−1=[12243145536776]
- 置换解密即使多次置换操作,仍不能加强保密性 。简单分析:因为多次置换操作的效果可以被一次等效的置换操作所取代。从攻击者角度看,他只需破解这最终的、唯一的置换,其面对的密钥空间并未增大。此外,置换只改变字符位置,不改变字符本身,因此无法抵御频率分析等统计攻击。这与替代加密的非线性特性有本质区别,多次替代能指数级增强保密性。
1.2 代换加密体系
-
代换密码(Substitution Cipher)是将明文中的字符替换成其他字符的密码体制。
-
基本方法:建立一个代换表,加密时将待加密的明文字符通过查表代换为对应的密文字符,代换表就是密钥。
-
定义 设 P P P、 C C C 和 K K K 分别为明文空间、密文空间和密钥空间。其中 P P P 和 C C C 是 26 个英文字母的集合, K K K 是由 26 个数字 0 , 1 , ... , 25 0,1,\ldots,25 0,1,...,25 的所有代换组成,对任何一个密钥 π ∈ K \pi \in K π∈K(即代换表),定义代换加密如下:
e π ( x ) = π ( x ) d π ( y ) = π − 1 ( y ) e_{\pi}(x) = \pi(x) \\ d_{\pi}(y) = \pi^{-1}(y) eπ(x)=π(x)dπ(y)=π−1(y)
π − 1 \pi^{-1} π−1 表示密钥 π \pi π 的逆代换, x x x 表示一个明文字符, y y y 表示一个密文字符。 -
按照一个明文字符是否总是被一个固定的字母代换,可将代换密码划分为两类:单表代换密码(Monoalphabetic Substitution Cipher)和多表代换密码(Polyalphabetic Substitution Cipher)。
1.3 单表代换密码
- 单表代换密码指明文中相同的字母,在加密时都使用同一个字母来代换。
- 移位密码:将 26 个英文字符从 a~z 依次分别与 0~25 的整数建立一一对应关系。令 P = C = K = Z 26 P = C = K = \mathbb{Z}_{26} P=C=K=Z26, x ∈ P , y ∈ C , k ∈ K x \in P, y \in C, k \in K x∈P,y∈C,k∈K,定义:
e k ( x ) = x + k m o d 26 d k ( y ) = y − k m o d 26 e_k(x) = x + k \mod 26 \\ d_k(y) = y - k \mod 26 ek(x)=x+kmod26dk(y)=y−kmod26 - 仿射密码:由于移位密码的密钥量太小,且代换表中字母先后次序没有改变,仿射密码可以改进这些弱点。
令 P = C = Z 26 P = C = \mathbb{Z}{26} P=C=Z26, K = { ( a , b ) ∈ Z 26 × Z 26 : gcd ( a , 26 ) = 1 } K = \{(a,b) \in \mathbb{Z}{26} \times \mathbb{Z}_{26} : \gcd(a,26) = 1\} K={(a,b)∈Z26×Z26:gcd(a,26)=1}, x ∈ P , y ∈ C , k = ( a , b ) ∈ K x \in P, y \in C, k = (a,b) \in K x∈P,y∈C,k=(a,b)∈K,定义:
e k ( x ) = a x + b m o d 26 d k ( y ) = a − 1 ( y − b ) m o d 26 e_k(x) = ax + b \mod 26 \\ d_k(y) = a^{-1}(y - b) \mod 26 ek(x)=ax+bmod26dk(y)=a−1(y−b)mod26要求 gcd ( a , 26 ) = 1 \gcd(a,26) = 1 gcd(a,26)=1,否则,加密函数就不是一个单射函数。例如当 k = ( 6 , 1 ) k = (6,1) k=(6,1) 时, gcd ( a , 26 ) = gcd ( 6 , 26 ) = 2 \gcd(a,26) = \gcd(6,26) = 2 gcd(a,26)=gcd(6,26)=2,对 x ∈ Z 26 x \in \mathbb{Z}_{26} x∈Z26,有 6 ( x + 13 ) + 1 = 6 x + 1 m o d 26 6(x + 13) + 1 = 6x + 1 \mod 26 6(x+13)+1=6x+1mod26,于是 x , x + 13 x, x + 13 x,x+13 都是 6 x + 1 6x + 1 6x+1 的明文。
-
gcd(α,26)=1时,仿射密码的解唯一。
-
当α=1时,仿射密码就退化为移位密码。
-
单表代换存在一个问题就是密文和明文间有着固定的代换关系。明文字符出现的频率没有掩盖,即明文中常出现的字符在密文中也常出现,于是被密码分析者所利用,从而达到破解的目的。在单表代换下,字母的频率、重复字母的模式和字母组合方式等统计特性(除了字母名称改变以外)均未改变。
-
密文分析时,可先统计密文中各个字母出现的频率,然后猜测出现次数最多的字母为e的密文,次多的字母为t,或者a,或者o。然后用这两个字母来替换密文,根据搭配关系、词首尾关系继续分析、猜测剩余的密文,最终得到全部的明文。
1.4 多表代换密码
- 多表代换密码是多个代换表依次对明文消息的字母进行代换的加密方法。
- 不妨设明文序列为 m = m 1 m 2 ... m = m_1 m_2 \ldots m=m1m2...,代换表序列为 π = π 1 , π 2 , ... , π d , π 1 , π 2 , ... , π d , ... \pi = \pi_1, \pi_2, \ldots, \pi_d, \pi_1, \pi_2, \ldots, \pi_d, \ldots π=π1,π2,...,πd,π1,π2,...,πd,...,于是,得到的密文序列为:
c = π ( m ) = π 1 ( m 1 ) , π 2 ( m 2 ) , ... , π d ( m d ) , π 1 ( m d + 1 ) , π 2 ( m d + 2 ) , ... , π d ( m 2 d ) , ... c = \pi(m) = \pi_1(m_1), \pi_2(m_2), \ldots, \pi_d(m_d), \pi_1(m_{d+1}), \pi_2(m_{d+2}), \ldots, \pi_d(m_{2d}), \ldots c=π(m)=π1(m1),π2(m2),...,πd(md),π1(md+1),π2(md+2),...,πd(m2d),...
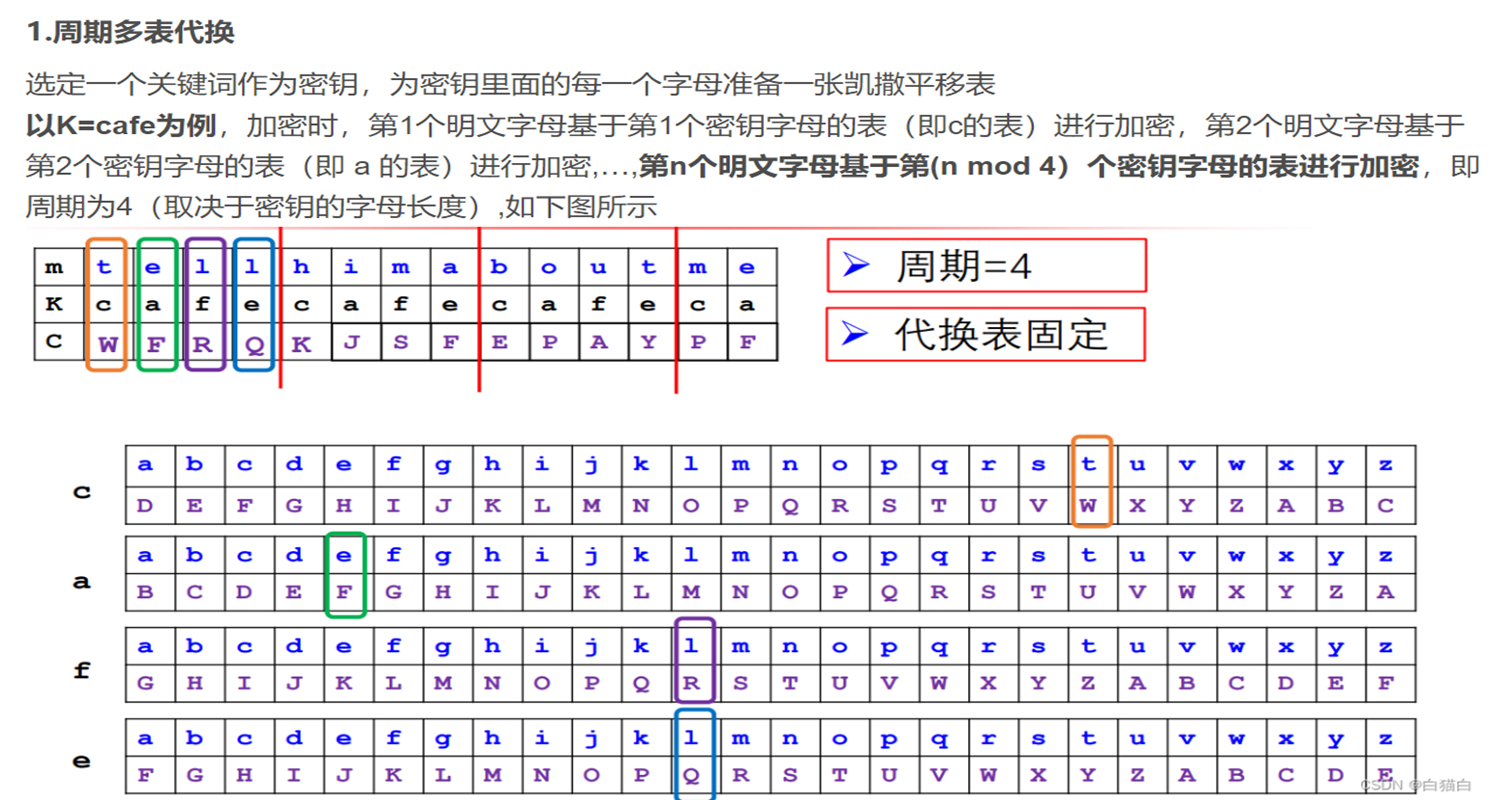
通俗地说,就是代换表的个数为 d d d,用不同的代换表来轮流代换明文消息中的字母。严格来说,这里 d d d 表示代换序列的周期。
-
用d代表代换表的数量,如果d=1,多表代换密码退化为单表代换密码,即只有一个代换表。
-
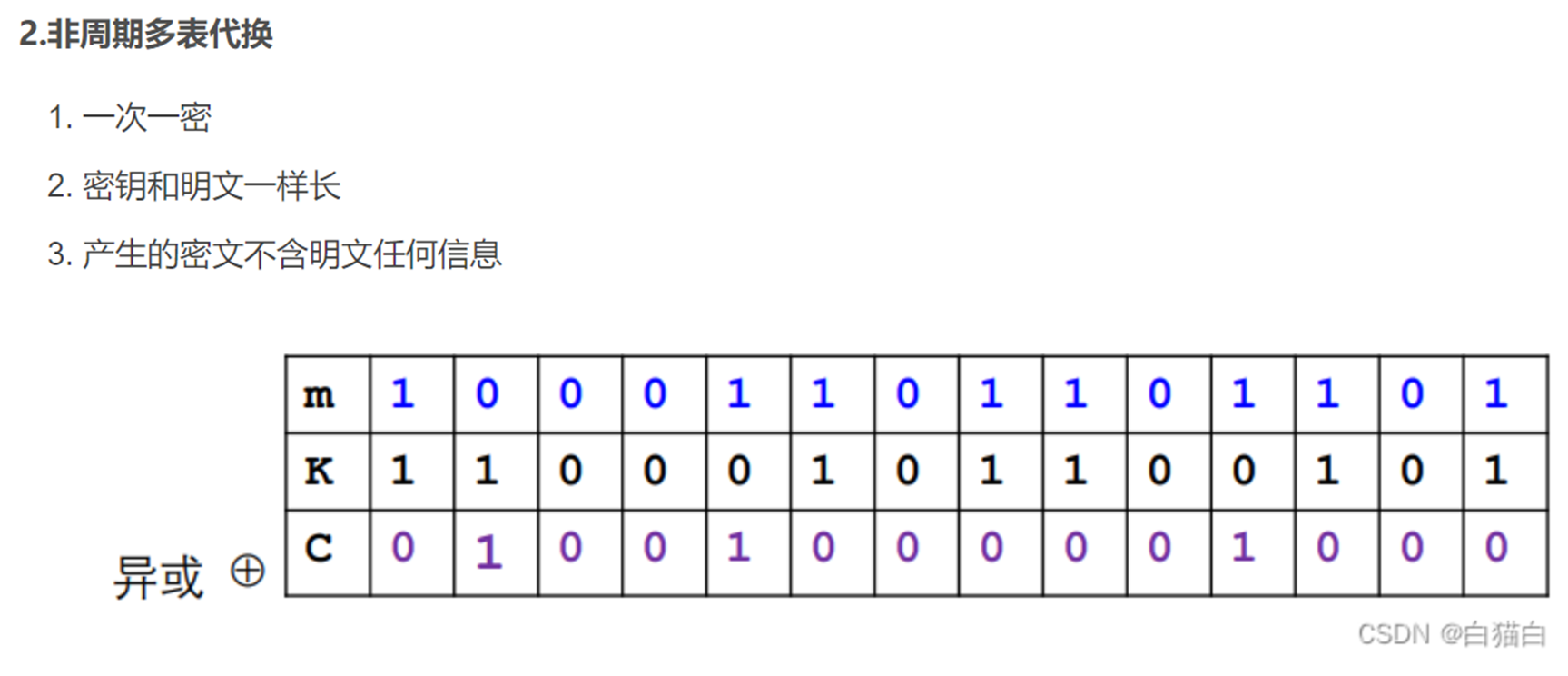
如果 d = ∞ d=\infty d=∞,则代换序列是非周期无限序列,每个明文都采用不同的代换表进行加密,这其实就是"一次一密"。通常实际应用中采用周期代换密码,也就是使用有限个代换表。
-
多表代换密码利用从明文字母到密文字母的多个映射,隐藏单字母的统计特征(如频率特征)。它将明文字母划分为长度相同的明文分组,然后对明文分组进行代换。这样,同一个字母只要在不同明文分组中的不同位置就会映射到不同的密文字母,从而更好地抵抗密码分析。
1.5 典型的多表代换密码算法
- 典型的多表代换密码算法有4种:Playfair密码、Vigenere密码、Vernam密码和Hill密码。
1.5.1 Playfair密码
- Playfair密码将明文按2个字母分成一组,每组根据代换表代换成其他两个字母。这里的代换表是一个 5 × 5 5 \times 5 5×5字母矩阵(I和J等价,于是共26个字母),该矩阵根据密钥构造,这里的密钥通常是一个关键词,假设如hello。构造矩阵的方法是:从左到右,从上到下依次填入关键词的字母,关键词中的重复字母第二次出现时略过,然后剩余字母按顺序填入矩阵。约定表中第一列视为第五列的右边一列,第一行视为第五行的下一行。每一对明文字母 p 1 , p 2 p_1, p_2 p1,p2分别替代成 c 1 , c 2 c_1, c_2 c1,c2的方法如下:
①如果 p 1 , p 2 p_1, p_2 p1,p2同行,则 c 1 , c 2 c_1, c_2 c1,c2为紧靠 p 1 , p 2 p_1, p_2 p1,p2右端的字母。
②如果 p 1 , p 2 p_1, p_2 p1,p2同列,则 c 1 , c 2 c_1, c_2 c1,c2为紧靠 p 1 , p 2 p_1, p_2 p1,p2下端的字母。
③如果 p 1 , p 2 p_1, p_2 p1,p2在不同行不同列,则确定了两个角,于是剩下的两个角为 c 1 , c 2 c_1, c_2 c1,c2,按照同行的原则对应; - 如果密钥为"hello",如何用Playfair密码加密"university"。先构造字母矩阵如下:
h e l o a b c d f g i / j k m n p q r s t u v w x y z \] \\begin{bmatrix} h \& e \& l \& o \& a \\\\ b \& c \& d \& f \& g \\\\ i/j \& k \& m \& n \& p \\\\ q \& r \& s \& t \& u \\\\ v \& w \& x \& y \& z \\end{bmatrix} hbi/jqveckrwldmsxofntyagpuz
1.5.2 Vigenere密码
-
定义 设 m m m为某个固定的正整数, P , C , K P, C, K P,C,K分别为明文空间、密文空间、密钥空间,且 P = C = K = ( Z 26 ) m P = C = K = (Z_{26})^m P=C=K=(Z26)m,对一个密钥 k = ( k 1 , k 2 , . . . , k m ) k = (k_1, k_2, ..., k_m) k=(k1,k2,...,km),定义:
e k ( x 1 , x 2 , . . . , x m ) = ( x 1 + k 1 , x 2 + k 2 , . . . , x m + k m ) e_k(x_1, x_2, ..., x_m) = (x_1 + k_1, x_2 + k_2, ..., x_m + k_m) ek(x1,x2,...,xm)=(x1+k1,x2+k2,...,xm+km)
d k ( y 1 , y 2 , . . . , y m ) = ( y 1 − k 1 , y 2 − k 2 , . . . , y m − k m ) d_k(y_1, y_2, ..., y_m) = (y_1 - k_1, y_2 - k_2, ..., y_m - k_m) dk(y1,y2,...,ym)=(y1−k1,y2−k2,...,ym−km)这里 ( x 1 , x 2 , . . . , x m ) (x_1, x_2, ..., x_m) (x1,x2,...,xm)为一个明文分组中的 m m m个字母。所有运算在 Z 26 Z_{26} Z26中进行。密钥长度为 m m m,故密钥空间为 2 6 m 26^m 26m。明文是按照长度为 m m m的分组进行加密的。
-
Vigenere密码是典型的多表代换,加密中一个字母可被映射到 m m m个可能的字母之一(假定密钥包括m个不同的字母),所以分析起来比单表代换更困难。
-
设m=5,密钥字为"hello",如何加密"university"。
-
明文分组为:unive,rsity,明文转化为 Z 26 Z_{26} Z26为:20,13,8,21,4和17,18,8,19,24.密钥字实际为k =(7,4,11,11,14),Z26表示的密文为:1,17,19,6,18和24,22,19,4,12。对应的密文字母为"brxgs, ywtem'。
使用Vigenere密码加密 "university" 的过程,其中密钥为 "hello" (m=5)。整个过程可以分为三个主要步骤:
- 准备阶段:将明文和密钥转换为数字。
- 加密计算:逐个分组进行模加法运算。
- 结果转换:将计算出的数字结果转换回字母。
第一步:准备阶段
- 字母到数字的映射表。在密码学中,通常使用
A=0, B=1, ..., Z=25的标准。
| 字母 | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 数字 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
1.1 分组明文
明文 "university" 的长度为10。密钥长度 m=5,所以我们将明文分成两组,每组5个字母:
- 第一组 :
unive - 第二组 :
rsity
1.2 转换明文
根据上面的映射表,将两组明文字母转换为数字:
- 第一组
unive:- u -> 20
- n -> 13
- i -> 8
- v -> 21
- e -> 4
- 所以,第一组明文数字为: (20, 13, 8, 21, 4)
- 第二组
rsity:- r -> 17
- s -> 18
- i -> 8
- t -> 19
- y -> 24
- 所以,第二组明文数字为: (17, 18, 8, 19, 24)
1.3 转换密钥
密钥为 "hello",同样转换为数字:
- h -> 7
- e -> 4
- l -> 11
- l -> 11
- o -> 14
- 所以,密钥数字为: k = (7, 4, 11, 11, 14)
第二步:加密计算
- Vigenere密码的加密公式为
密文 = (明文 + 密钥) mod 26。我们将用这个公式对每个分组进行计算。
2.1 加密第一组 unive (20, 13, 8, 21, 4)
- 第1个字母 :
20 + 7 = 2727 mod 26 = 1
- 第2个字母 :
13 + 4 = 1717 mod 26 = 17
- 第3个字母 :
8 + 11 = 1919 mod 26 = 19
- 第4个字母 :
21 + 11 = 3232 mod 26 = 6
- 第5个字母 :
4 + 14 = 1818 mod 26 = 18
所以,第一组加密后的数字为: (1, 17, 19, 6, 18)
2.2 加密第二组 rsity (17, 18, 8, 19, 24)
- 第1个字母 :
17 + 7 = 2424 mod 26 = 24
- 第2个字母 :
18 + 4 = 2222 mod 26 = 22
- 第3个字母 :
8 + 11 = 1919 mod 26 = 19
- 第4个字母 :
19 + 11 = 3030 mod 26 = 4
- 第5个字母 :
24 + 14 = 3838 mod 26 = 12
所以,第二组加密后的数字为: (24, 22, 19, 4, 12)
第三步:结果转换
- 将计算出的两组密文数字转换回字母。
3.1 转换第一组密文 (1, 17, 19, 6, 18)
- 1 -> B
- 17 -> R
- 19 -> T
- 6 -> G
- 18 -> S
- 第一组密文为: "brtgs" (注:您提供的示例中为"brxgs",其中第三个字母的计算可能有误,应为19->T)
3.2 转换第二组密文 (24, 22, 19, 4, 12)
- 24 -> Y
- 22 -> W
- 19 -> T
- 4 -> E
- 12 -> M
- 第二组密文为: "ywtem"
将两组密文拼接起来,得到最终的密文。
| 分组 | 明文 | 明文数字 | 密钥 | 密钥数字 | 计算过程 (P+K) mod 26 | 密文数字 | 密文 |
|---|---|---|---|---|---|---|---|
| 1 | unive |
(20, 13, 8, 21, 4) | hello |
(7, 4, 11, 11, 14) | (1, 17, 19, 6, 18) | (1, 17, 19, 6, 18) | brtgs |
| 2 | rsity |
(17, 18, 8, 19, 24) | hello |
(7, 4, 11, 11, 14) | (24, 22, 19, 4, 12) | (24, 22, 19, 4, 12) | ywtem |
因此,使用密钥 "hello" 对明文 "university" 进行Vigenere加密,得到的最终密文是 brtgsywtem。
1.5.3 Vernam密码
定义 2.6 设加密的明文为 p = p 1 p 2 ⋯ p i ⋯ p = p_1p_2 \cdots p_i \cdots p=p1p2⋯pi⋯,密钥为 k = k 1 k 2 ⋯ k i ⋯ k = k_1k_2 \cdots k_i \cdots k=k1k2⋯ki⋯,其中 p i , k i ∈ G F ( 2 ) , i ≥ 1 p_i, k_i \in GF(2), i \geq 1 pi,ki∈GF(2),i≥1,则密文 c = c 1 c 2 ⋯ c i ⋯ c = c_1c_2 \cdots c_i \cdots c=c1c2⋯ci⋯有
c i = m i ⊕ k i , i ≥ 1 c_i = m_i \oplus k_i, i \geq 1 ci=mi⊕ki,i≥1
这里 ⊕ \oplus ⊕为模2加法。
- Vermam 无法经受已知明文攻击,这是因为k=m Ci, ≥ 1,只要知道了某些明文密文对,便可以迅速确定相应的密钥。如果同一个密钥被重复使用,密码分析者可以立即解密密文得到明文。
- 为了避免密钥本身的重复,一种极端情况是:①密钥是真正的随机序列;②密钥至少和明文一样长;③一个密钥只使用一次。如果这样,密码就是不可破译的,这便是著名的"一次一密"(one time pad)。然而"一次一密"在实际上是行不通的,需要经常产生、存储、安全传递大量的很长的密钥,这在实际中是及其困难的。
15.4 Hill密码
-
希尔密码(Hill Cipher)基本思想是把m个连续的明文字母代换成 m m m个连续的密文字母,这个代换由密钥决定,这个密钥是一个变换矩阵,解密时只需要对密文做一次逆变换即可。
-
定义2.7 设 m m m是某个固定的正整数, P , C , K P, C, K P,C,K分别为明文空间、密文空间、密钥空间,且 P = C = ( Z 26 ) m P = C = (Z_{26})^m P=C=(Z26)m,设 K = ( k i j ) m × m \mathbf{K} = (k_{ij})_{m \times m} K=(kij)m×m是一个 m × m m \times m m×m可逆矩阵,(即行列式 d e t ( K ) ≠ 0 det(\mathbf{K}) \neq 0 det(K)=0,且 g c d ( 26 , d e t ( K ) = 1 ) gcd(26, det(\mathbf{K}) = 1) gcd(26,det(K)=1))。对任意密钥 k ∈ K k \in K k∈K,定义:
e k ( x ) = x K e_k(x) = x\mathbf{K} ek(x)=xK
d k ( y ) = y K − 1 d_k(y) = y\mathbf{K}^{-1} dk(y)=yK−1所有运算均在 Z 26 Z_{26} Z26中进行。
-
设 m = 2 m = 2 m=2,密钥 K = [ 11 8 3 7 ] \mathbf{K} = \begin{bmatrix} 11 & 8 \\ 3 & 7 \end{bmatrix} K=[11387],容易计算 K − 1 = [ 7 18 23 11 ] \mathbf{K}^{-1} = \begin{bmatrix} 7 & 18 \\ 23 & 11 \end{bmatrix} K−1=[7231811],设明文为hill,相应的明文向量为 [ 7 , 8 ] [7, 8] [7,8]和 [ 11 , 11 ] [11, 11] [11,11],于是,相应的密文向量分别为
7 , 8 \] \[ 11 8 3 7 \] = \[ 77 + 24 , 56 + 56 \] = \[ 23 , 8 \] , \[7, 8\] \\begin{bmatrix} 11 \& 8 \\\\ 3 \& 7 \\end{bmatrix} = \[77 + 24, 56 + 56\] = \[23, 8\], \[7,8\]\[11387\]=\[77+24,56+56\]=\[23,8\], \[ 11 , 11 \] \[ 11 8 3 7 \] = \[ 121 + 33 , 88 + 77 \] = \[ 24 , 9 \] , \[11, 11\] \\begin{bmatrix} 11 \& 8 \\\\ 3 \& 7 \\end{bmatrix} = \[121 + 33, 88 + 77\] = \[24, 9\], \[11,11\]\[11387\]=\[121+33,88+77\]=\[24,9\], 故密文为xiyj。
1.6 多表代换密码的统计分析
- 与单表代换密码相比,多表代换密码虽然能抵御简单的统计分析,但是,如果密码分析者能够确定密钥的长度,则多表代换密码的分析就可转变成为单表代换密码的分析。
- 观察密文中重复出现的密文字母片段来估计密钥的长度,即找出相同密文片段的间隔数,然后求最大公因子,可能是密钥的长度。
- 古典密码体制一般只能承受唯密文攻击,不能承受已知明文攻击。
二 现代密码学的三条原则
- 安全和威胁模型的严格定义的形式化。
- 当一个加密方案的安全依赖于无法证明的假设时,这个假设必须被精确地描述并且尽可能地小。
- 加密方案应该带有一个基于以上定义和假设对安全性的严格证明。