了解了神经网络的结构之后,这里我们来进行手写数字图像的分类。神经网络的"推理处理"。这个推理处理也称为神经网络的前向 传播(forward propagation)。
使用神经网络解决问题时,需要首先使用训练数据(学习数据)进行权重参数的学习;
进行推理时,使用刚才学习到的参数,对输入数据进行分类。

本文章知识来源于《深度学习入门》 (鱼书),特此声明。可以当做读数笔记来进行阅读。
1.MNIST数据集
这里使用的数据集是MNIST手写数字图像集。MNIST是机器学习领域最有名的数据集之一,被应用于从简单的实验到发表的论文研究等各种场合。 实际上,在阅读图像识别或机器学习的论文时,MNIST数据集经常作为实验用的数据出现。
1.2 下载
官方已经无法下载,这里可以 clone github仓库
shell
git clone https://github.com/knamdar/data.git
| 文件名称 | 内容 |
|---|---|
| train-images-idx3-ubyte.gz | 55000张训练集,5000张验证集 |
| train-labels-idx1-ubyte.gz | 训练集图片对应的标签 |
| t10k-images-idx3-ubyte.gz | 10000张测试集 |
| t10k-labels-idx1-ubyte.gz | 测试集图片对应的标签 |
在上述文件中,训练集train一共包含了 60000 张图像和标签,而测试集一共包含了 10000 张图像和标签。
idx3表示3维,ubyte表示是以字节的形式进行存储的,t10k表示10000张测试图片(test10000)。
每张图片是一个28*28 像素点的0 ~ 9 的灰质手写数字图片,黑底白字,图像像素值为0 ~ 255,越大该点越白。
1.3 加载数据集文件
python
import os
import struct
import numpy as np
import matplotlib.pyplot as plt
def load_mnist(path, kind='train'):
"""Load MNIST data from `path`"""
labels_path = os.path.join(path,
'%s-labels-idx1-ubyte'
% kind)
images_path = os.path.join(path,
'%s-images-idx3-ubyte'
% kind)
with open(labels_path, 'rb') as lbpath:
# 前4个字节是magic number
# 接下来4 个字节是有多少个图片,比如 60000
# 所以先读取了 8个字节,前四个字节存入了 magic中, 后四个字节存入了 n中
# ">II" 解读: ">" 表示按大端读取,
# "I" 这是指一个无符号整数
magic, n = struct.unpack('>II',
lbpath.read(8))
# 每个图片的标签
labels = np.fromfile(lbpath,
dtype=np.uint8)
with open(images_path, 'rb') as imgpath:
# 4个 4字节,分别表示 magic, num,rows,cols
magic, num, rows, cols = struct.unpack('>IIII',
imgpath.read(16))
# 每一行是一个图片,有 784列,因为每个图片是 28 x 28 = 784
images = np.fromfile(imgpath,
dtype=np.uint8).reshape(len(labels), 784)
return images, labels1.4 可视化显示图片
将训练集前10张图片显示出来。
python
if __name__ == '__main__':
# train_images n x m 的 NumPy array
# n 是样本数(行数) ,m是特征数(列数)
# 数据集中的每张图片由 28 x 28 个像素点构成, 每个像素点用一个灰度值表示. 在这里, 我们将 28 x 28 的像素展开为一个一维的行向量, 这些行向量就是图片数组里的行(每行 784 个值, 或者说每行就是代表了一张图片)
# train_labels 包含了相应的目标变量, 也就是手写数字的类标签(整数 0-9).
(train_images ,train_labels )=load_mnist('./data/MNIST/raw')
print(f'训练集:{train_images.shape}, {train_labels.shape[0]}张图片')
fig, ax = plt.subplots(
nrows=2,
ncols=5,
sharex=True,
sharey=True, )
ax = ax.flatten()
for i in range(10):
img = train_images[i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[i].title.set_text(train_labels[i])
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()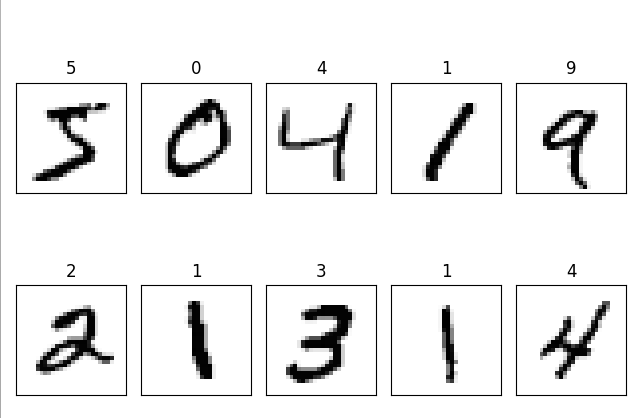
1.5 归一化处理(Normalization)
通过一些转换函数 将特征数据转换成更加适合算法模型的特征数据过程.
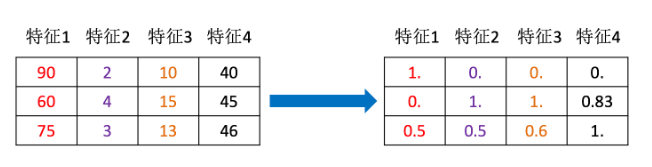
为什么我们要进行归一化/标准化?
特征的单位或者大小相差较大,或者某特征的方差相比其他的特征要大出几个数量级 ,容易影响(支配)目标结果,使得一些算法无法学习到其它的特征
上面加载数据集数据的时候,每个图片有 **28*28**个像素,其值为 0-255 (含0和 255),我们可以采用每个像素除以255的办法对其进行归一化,使得数据被缩放到 [0,1] 的范围
python
def load_mnist(path, kind='train', normalize=True):
"""Load MNIST data from `path`"""
labels_path = os.path.join(path,
'%s-labels-idx1-ubyte'
% kind)
images_path = os.path.join(path,
'%s-images-idx3-ubyte'
% kind)
with open(labels_path, 'rb') as lbpath:
# 前4个字节是magic number
# 接下来4 个字节是有多少个图片,比如 60000
# 所以先读取了 8个字节,前四个字节存入了 magic中, 后四个字节存入了 n中
# ">II" 解读: ">" 表示按大端读取,
# "I" 这是指一个无符号整数
magic, n = struct.unpack('>II',
lbpath.read(8))
# 每个图片的标签
labels = np.fromfile(lbpath,
dtype=np.uint8)
with open(images_path, 'rb') as imgpath:
# 4个 4字节,分别表示 magic, num,rows,cols
magic, num, rows, cols = struct.unpack('>IIII',
imgpath.read(16))
# 每一行是一个图片,有 784列,因为每个图片是 28 x 28 = 784
images = np.fromfile(imgpath,
dtype=np.uint8).reshape(len(labels), 784)
# 归一化处理
if normalize:
images = images.astype(np.float32) / 255.0
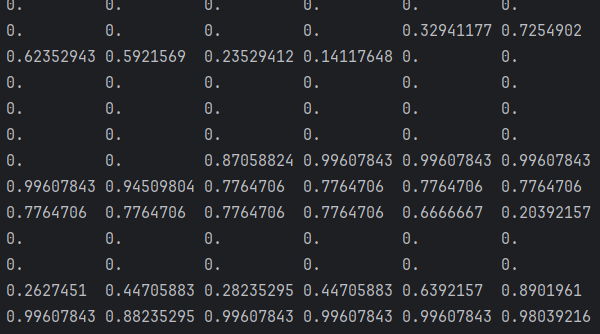
return images, labels没有做归一化,取出测试数据集中的第1条记录,打印内容,会发现其值的返回都是 0-255

做归一化后,再打印,会发现其范围已经是 [0,1] 的数据了:
2.搭建网络推理
我们的任务,就是要搭建一个神经网络,实现它的前向传播;也就是要根据输入的数据 (28X28=784数据点表示的图像),推断出它到底是哪个数字,这个过程也被称为"推理"。
- 输入层: 784个神经元
- 中间设置2个隐藏层: 第一个隐藏层 50个神经元,第二个隐藏层 100个神经元。
- 输出层有 10个身影元(表示0-9的分类结果 )
权重参数是需要经过
学习得到的,这里假设已经学习完毕, 权重参数在data/MNIST/sample_weight.pkl文件中,我们只需要加载权重文件即可获取权重参数数据。
sample_weight.pkl 这个文件我是到 https://github.com/oreilly-japan/deep-learning-from-scratch/tree/master/ch03 中下载的。
2.1 加载测试集数据
上面介绍了 MNIST数据集,其中包含了 训练集和测试集,这里是要进行预测,所以我们只需要加载测试集即可。
neuralnet_mnist.py文件:
python
import os
import struct
import numpy as np
import matplotlib.pyplot as plt
# 训练集传 train, 测试集传 t10k (有 10K 即 10000个图片的测试数据集)
def load_mnist(path, kind='train'):
"""Load MNIST data from `path`"""
labels_path = os.path.join(path,
'%s-labels-idx1-ubyte'
% kind)
images_path = os.path.join(path,
'%s-images-idx3-ubyte'
% kind)
with open(labels_path, 'rb') as lbpath:
# 前4个字节是magic number
# 接下来4 个字节是有多少个图片,比如 60000
# 所以先读取了 8个字节,前四个字节存入了 magic中, 后四个字节存入了 n中
# ">II" 解读: ">" 表示按大端读取,
# "I" 这是指一个无符号整数
magic, n = struct.unpack('>II',
lbpath.read(8))
# 每个图片的标签
labels = np.fromfile(lbpath,
dtype=np.uint8)
with open(images_path, 'rb') as imgpath:
# 4个 4字节,分别表示 magic, num,rows,cols
magic, num, rows, cols = struct.unpack('>IIII',
imgpath.read(16))
# 每一行是一个图片,有 784列,因为每个图片是 28 x 28 = 784
images = np.fromfile(imgpath,
dtype=np.uint8).reshape(len(labels), 784)
return images, labels
if __name__ == '__main__':
x_test,y_test=load_mnist('./data/MNIST/raw','t10k')
# x_test.shape:(10000, 784) y_test.shape:(10000,)
# x_test.shape 10000张图片,每个图片 28 x 28 =784 个像素
# y_test.shape 10000张图片的标签
print(f'x_test.shape:{x_test.shape} y_test.shape:{y_test.shape}')2.2 初始化神经网络
主要是加载权重文件
python
def init_neural_network():
'''
初始化神经网络
:return:
'''
model=joblib.load('./data/MNIST/sample_weight.pkl')
print(f'{model.keys()}') # dict_keys(['b2', 'W1', 'b1', 'W2', 'W3', 'b3'])
print(f'W1:{model["W1"].shape} b1:{model["b1"].shape} , '
f' W2:{model["W2"].shape} b2:{model["b2"].shape},'
f' W3:{model["W3"].shape} b3:{model["b3"].shape}')
return model
if __name__ == '__main__':
neural_network=init_neural_network()
print(type(neural_network)) # <class 'dict'>
# neural_network 中所有的key执行后输出:
latex
dict_keys(['b2', 'W1', 'b1', 'W2', 'W3', 'b3'])
W1:(784, 50) b1:(50,) , W2:(50, 100) b2:(100,), W3:(100, 10) b3:(10,)这说明: sample_weight.pkl中包含了3个权重参数:W1,W2,W3,三个偏置参数b1,b2,b3 即:
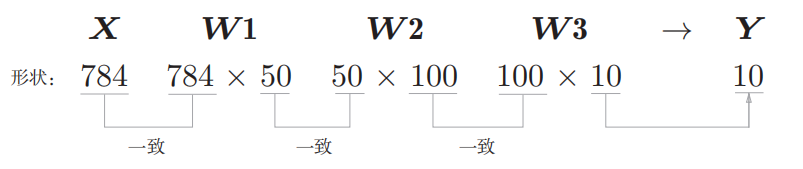
2.3 推理函数
推理的过程中,需要用到 激活函数,这里创建一个 common包,在这个包中定义激活函数
common/functions.py
python
import numpy as np
def sigmoid_function(x):
"""
Sigmoid 激活函数
:param x:
:return:
"""
return 1 / (1 + np.exp(-x))
def softmax(a):
'''
假设 a =np.array([0.3,2.9,4.0])
:param a:
:return:
'''
# 分子:输入信号ak的指数函数
exp_a=np.exp(a) # [ 1.34985881 18.17414537 54.59815003]
# 分母: 输入信号指数函数的和
sum_exp_a=np.sum(exp_a) # 74.1221542102
y=exp_a/sum_exp_a # [ 0.01821127 0.24519181 0.73659691]
return y推理函数:
python
def predict(neural_network,x):
W1,W2,W3=neural_network['W1'],neural_network['W2'],neural_network['W3']
b1,b2,b3=neural_network['b1'],neural_network['b2'],neural_network['b3']
A1=np.dot(x,W1)+b1
Z1=common.sigmoid_function(A1)
A2=np.dot(Z1,W2)+b2
Z2=common.sigmoid_function(A2)
A3=np.dot(Z2,W3)+b3
return common.softmax(A3)2.4 执行推理
- 加载测试数据集
- 初始化网络,从权重文件中加载权重参数
- 预测/推理
- 输出预测结果
python
if __name__ == '__main__':
# 1. 加载测试集数据
x_test,y_test=load_mnist('./data/MNIST/raw','t10k')
# 2. 初始化网络,从权重文件中加载权重参数
neural_network=init_neural_network()
# 3. 预测
# 从测试数据集中取出10个样本进行预测
x_test_sample=x_test[:10]
y_test_sample=y_test[:10]
accuracy_cnt = 0 # 用于统计预测正确的数量
for i in range(len(x_test_sample)):
print(f'第{i}个样本的标签为:{y_test_sample[i]}')
result=predict(neural_network,x_test_sample[i])
# 获取概率最高的元素的索引
argmax_index=np.argmax(result)
print(f'第{i}个样本的预测结果为:{result}, 概率最高的元素的索引:{argmax_index}')
if y_test_sample[i] == argmax_index:
accuracy_cnt += 1
print("="*50)
print("Accuracy:" + str(float(accuracy_cnt) / len(x_test_sample)))
python
第0个样本的标签为:7
第0个样本的预测结果为:[4.2878996e-06 4.5729305e-07 1.8486274e-04 8.3604988e-05 1.5084682e-07
6.3182210e-07 4.5782003e-10 9.9919480e-01 3.8066918e-07 5.3083024e-04], 概率最高的元素的索引:7
==================================================
第1个样本的标签为:2
第1个样本的预测结果为:[3.6033167e-04 1.1461668e-03 9.8586732e-01 6.4584352e-03 9.2993112e-08
7.3918235e-04 5.1419172e-03 2.6647359e-07 2.8627011e-04 4.1333013e-09], 概率最高的元素的索引:2
==================================================
...
第9个样本的标签为:9
第9个样本的预测结果为:[2.0611069e-05 3.3467338e-06 8.6421822e-04 6.6968198e-05 3.1582799e-02
6.2435276e-05 7.6674960e-06 2.4675315e-02 2.3410693e-02 9.1930592e-01], 概率最高的元素的索引:9
==================================================
Accuracy:0.9可以看到最后输出的准确率为 : 90% ,这只是取了测试集中前 10 个测试数据进行测试。你可以调整测试样本数量。
2.5 批量处理
上面推理的时候,图片只能一张一张的推理,每次推理的形状是这样的:
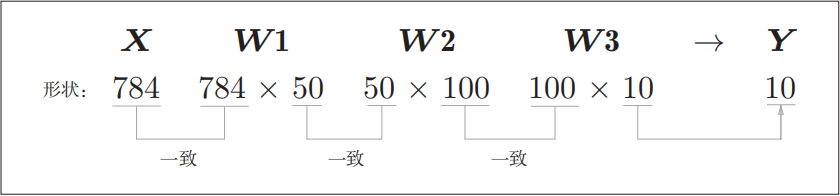
从整体的处理流程来看,输入一个由784个元素(原本是一 个28 _× _28的二维数组)构成的一维数组后,输出一个有10个元素的一维数组。 这是只输入一张图像数据时的处理流程。
现在我们来考虑打包输入多张图像的情形。比如,我们想用predict() 函数一次性打包处理100张图像。为此,可以把_x_的形状改为100 _× _784,将 100张图像打包作为输入数据。用图表示的话:
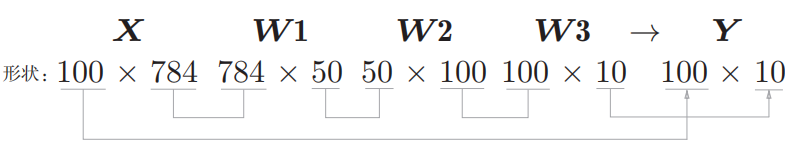
输入数据的形状为 100 _× _784,输出数据的形状为 100 _× _10。这表示输入的100张图像的结果被一次性输出了。
这种打包式的输入数据称为批(batch)。批有"捆"的意思,图像就如同纸币一样扎成一捆。批处理对计算机的运算大有利处,可以大幅缩短每张图像的处理时间。那么为什么批处理可以缩短处理时间呢?这是因为大多数处理数值计算的库都进行了能够高效处理大型数组运算的最优化。
在动手修改代码之前,先理解一下 python的 rage函数:
python
# range()函数若指定为range(start, end),则会生成一个由start到end-1之间的整数构成的列表。
>>> list(range(0, 10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> list(range(0, 10,3))
[0, 3, 6, 9]在range()函数生成的列表的基础上,通过x[i:i+batch_size]从输入数 据中抽出批数据。x[i:i+batch_n]会取出从第i个到第i+batch_n个之间的数据。 本例中是像x[0:100]、x[100:200]......这样,从头开始以100为单位将数据提取为批数据。
再看看argmax(x, axis)函数:
python
>>> import numpy as np
>>> x = np.array([[0.1, 0.8, 0.1],
[0.3, 0.1, 0.6],
[0.2, 0.5, 0.3],
[0.8, 0.1, 0.1]])
>>> y=np.argmax(x,axis=1)
>>> print(y)
[1 2 1 0]指定了 axis=1 表示在一维维度上进行计算(0 维度是行,1维度是列),可以这样理解: 0维度:
1 维度,就是列: 将每一列上的数据"串"起来后为轴。即以行为轴
比如上面:
第一行所有列"串起来",作为轴,有三个数: [0.1,0.8,0.1] 最大值是 0.8, 所在的索引就是 1
第二行所有列"串起来",作为轴,有三个数: [0.3,0.1,0.6] 最大值是 0.6, 所在的索引就是 2
第三行所有列"串起来",作为轴,有三个数: [0.2,0.5,0.3] 最大值是 0.5, 所在的索引就是 1
第四行所有列"串起来",作为轴,有三个数: [0.8,0.1,0.1] 最大值是 0.8, 所在的索引就是 0
所以最终结果就是 : [1 2 1 0]
按照这个思路,可以推导出来 y=np.argmax(x,axis=0)的结果是 [3,0,1]
latex
# 原始形状 (m, n)
# axis=0 结果形状: (n,) # 行维度消失
# axis=1 结果形状: (m,) # 列维度消失
# 记住:指定哪个 axis,结果中那个维度就会消失NumPy 数组之间的比较:
对应索引位置上的数据进行比较,比较后的结果维度不会发生变化
python
>>> y=np.array([1,2,1,0])
>>> t=np.array([1,2,0,0])
>>> print(y==t)
[ True True False True]完整代码:
python
if __name__ == '__main__':
# 1. 加载测试集数据
x_test,y_test=load_mnist('./data/MNIST/raw','t10k',True)
# print(x_test[0])
# 2. 初始化网络,从权重文件中加载权重参数
neural_network=init_neural_network()
# 3. 预测
# 从测试数据集中取出前200个样本进行预测,刚好构成 2个批次
x_test_sample=x_test[:200]
y_test_sample=y_test[:200]
batch_size=100 # 每批预测 100个样本
accuracy_cnt = 0 # 用于统计预测正确的数量
# [0,100,200,300...]
for i in range(0,len(x_test_sample),batch_size):
# 取出一批样本,即100 个样本
x_batch=x_test_sample[i:i+batch_size]
label_batch=y_test_sample[i:i+batch_size]
print(f'{i}:{i+batch_size} 批样本的标签为:{label_batch}')
result=predict(neural_network,x_batch)
# 获取概率最高的元素的索引
argmax_index=np.argmax(result,axis=1)
print(f'{i}:{i+batch_size} 概率最高的元素的索引:{argmax_index}')
accuracy_cnt += np.sum(argmax_index==label_batch)
print("="*50)
print("Accuracy:" + str(float(accuracy_cnt) / len(x_test_sample)))输出:
latex
0:100 批样本的标签为:[7 2 1 0 4 1 4 9 5 9 0 6 9 0 1 5 9 7 3 4 9 6 6 5 4 0 7 4 0 1 3 1 3 4 7 2 7
1 2 1 1 7 4 2 3 5 1 2 4 4 6 3 5 5 6 0 4 1 9 5 7 8 9 3 7 4 6 4 3 0 7 0 2 9
1 7 3 2 9 7 7 6 2 7 8 4 7 3 6 1 3 6 9 3 1 4 1 7 6 9]
0:100 概率最高的元素的索引:[7 2 1 0 4 1 4 9 6 9 0 6 9 0 1 5 9 7 3 4 9 6 6 5 4 0 7 4 0 1 3 1 3 6 7 2 7
1 2 1 1 7 4 2 3 5 1 2 4 4 6 3 5 5 6 0 4 1 9 5 7 8 9 3 7 4 2 4 3 0 7 0 2 9
1 7 3 2 9 7 7 6 2 7 8 4 7 3 6 1 3 6 4 3 1 4 1 7 6 9]
==================================================
100:200 批样本的标签为:[6 0 5 4 9 9 2 1 9 4 8 7 3 9 7 4 4 4 9 2 5 4 7 6 7 9 0 5 8 5 6 6 5 7 8 1 0
1 6 4 6 7 3 1 7 1 8 2 0 2 9 9 5 5 1 5 6 0 3 4 4 6 5 4 6 5 4 5 1 4 4 7 2 3
2 7 1 8 1 8 1 8 5 0 8 9 2 5 0 1 1 1 0 9 0 3 1 6 4 2]
100:200 概率最高的元素的索引:[6 0 5 4 9 9 2 1 9 4 8 7 3 9 7 4 4 4 9 2 5 4 7 6 4 9 0 5 8 5 6 6 5 7 8 1 0
1 6 4 6 7 3 1 7 1 8 2 0 9 9 9 5 5 1 5 6 0 3 4 4 6 5 4 6 5 4 5 1 4 4 7 2 3
2 7 1 8 1 8 1 8 5 0 8 9 2 5 0 1 1 1 0 9 0 3 1 6 4 2]
==================================================
Accuracy:0.97