【强化学习】第三章 马尔可夫决策过程

马尔可夫决策过程

• 马尔可夫过程
• • 随机过程
  • 马尔可夫性质
  • 马尔可夫过程
• 马尔可夫奖励过程
• • 回报
  • 价值函数
• 马尔可夫决策过程
• • 策略
  • 状态价值函数
  • 动作价值函数
  • 贝尔曼期望方程
• 蒙特卡洛方法
• 占有度量
• 最优策略
• 贝尔曼最优方程
• • 状态价值的贝尔曼最优方程公式
  • 动作价值的贝尔曼最优方程公式

来一个马尔可夫链，以前学过，再来温习。马尔可夫决策包含信息以及状态之间的转移机制，要用强化学习解决一个实际问题，首先要做的就是把实际问题抽象为一个马尔可夫决策过程，明确马尔可夫决策过程的各个组成要素。

马尔可夫过程

随机过程

随机过程研究对象是随着时间演变的随机现象

• S t S_t St：表示 t 时刻的随机变量（状态）
• S S S：表示所有可能的状态组成的状态集合
• P ( S t + 1 ∣ S 1 , . . . , S t ) P (S_{t+1}|S_1,...,S_t) P(St+1∣S1,...,St)：已知历史信息 ( S 1 , . . . , S t ) (S_1,...,S_t) (S1,...,St) 时下一个时刻状态为 S t + 1 S_{t+1} St+1 的概率。

马尔可夫性质

当且仅当某时刻的状态只取决于上一时刻的状态时，一个随机过程被称为具有马尔可夫性质 （Markov property），用公式表示为 P ( S t + 1 ∣ S t ) = P ( S t + 1 ∣ S 1 , . . . , S t ) P (S_{t+1}|S_t)=P (S_{t+1}|S_1,...,S_t) P(St+1∣St)=P(St+1∣S1,...,St)。

马尔可夫过程

马尔可夫过程 指马尔可夫性质的随机过程，也叫马尔可夫链 。元组 < S , P > <S,P> <S,P>描述一个马尔可夫过程，其中S是有限数量的状态集合，P是状态转移矩阵 （state transition matrix）。转移矩阵如下：
P = P ( s 1 ∣ s 1 ) . . . P ( s n ∣ s 1 ) . . . . . . . . . P ( s 1 ∣ s n ) . . . P ( s n ∣ s n ) P=\begin{bmatrix} P(s_1|s_1) & ... & P(s_n|s_1)\\ ...& ... &... \\ P(s_1|s_n)&... & P(s_n|s_n) \end{bmatrix} P= P(s1∣s1)...P(s1∣sn).........P(sn∣s1)...P(sn∣sn)

矩阵 P P P中第 i i i行第 j j j列元素 P ( s j ∣ s i ) = P ( S t + 1 = s j ∣ S t = s i ) P(s_j|s_i)=P(S_{t+1}=s_j|S_t=s_i) P(sj∣si)=P(St+1=sj∣St=si)表示从状态 s i s_i si转移到状态 s j s_j sj的概率，我们称 P ( s ′ ∣ s ) P(s'|s) P(s′∣s)为状态转移函数，每一行的和为1。

一个简单例子， S 6 S_6 S6通常为终止状态 。

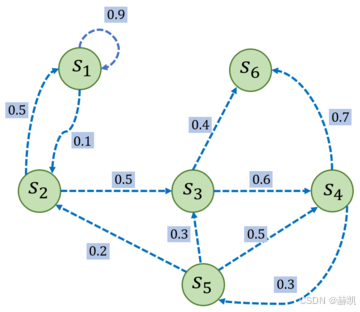
P = 0.9 0.1 0 0 0 0 0.5 0 0.5 0 0 0 0 0 0 0.6 0 0.4 0 0 0 0 0.3 0.7 0 0.2 0.3 0.5 0 0 0 0 0 0 0 1 P=\begin{bmatrix} 0.9 & 0.1&0&0&0& 0\\ 0.5& 0 &0.5&0&0&0 \\ 0&0&0&0.6&0&0.4\\ 0&0&0&0&0.3&0.7\\ 0&0.2&0.3&0.5&0&0\\ 0&0&0&0&0&1\\ \end{bmatrix} P= 0.90.500000.10000.2000.5000.30000.600.500000.300000.40.701

给定马尔可夫过程，我们就可以从某个状态出发，根据它的状态转移矩阵生成一个状态序列 （episode），这个步骤也被叫做采样（sampling）。

马尔可夫奖励过程

在此基础上加入奖励函数 r r r和折扣因子 γ γ γ，即为马尔可夫奖励过程。

• S = 有限状态的集合（所有可能的工作岗位）
• P = 状态转移矩阵（从一个岗位跳槽到另一个岗位的可能性）
• r = 奖励函数，某个状态s的奖励 r ( s ) r(s) r(s) 指转移到该状态时可以获得奖励的期望（每个岗位的薪资水平）
• γ = 是折扣因子（discount factor），的取值范围为[0,1)，有时候需要一些不确定性，接近1的γ更关注长期累积奖励，接近0的γ更考虑短期奖励。（你对长期职业发展的重视程度）

回报

从某个时刻的状态出发，一直到结束，所有 "奖励" 加起来的总和（但后面的奖励会 "打折"）
G t = R t + γ R t + 1 + γ 2 R t + 2 + ⋯ = ∑ k = 0 ∞ γ k R t + k G_ t =R _ t +γR_ {t+1} +γ ^2 R_ {t+2} +⋯=∑_ {k=0} ^∞ γ ^k R_ {t+k} Gt=Rt+γRt+1+γ2Rt+2+⋯=k=0∑∞γkRt+k

• G t G_t Gt：从第 t 时刻状态开始的 "回报"
• R t R_t Rt：第 t 时刻（当前状态），拿到的奖励
• γ \gamma γ："折扣因子"（0 到 1 之间的数），用来给后面的奖励 "打折"（比如 γ = 0.5 \gamma=0.5 γ=0.5，下一个时刻的奖励只算一半）
• γ k R t + k \gamma^k R_{t+k} γkRt+k：第 t + k t+k t+k时刻的奖励，打了 γ k \gamma^k γk的折
  
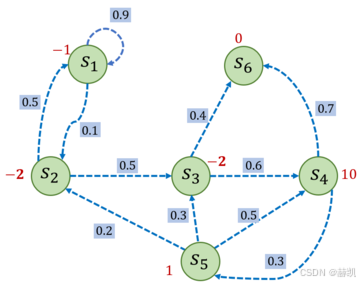
  如果路径是 s 1 − > s 2 − > s 3 − > s 6 s_1->s_2->s_3->s_6 s1−>s2−>s3−>s6，换算成公式就是： G 1 = − 1 + 0.5 × ( − 2 ) + 0. 5 2 × ( − 2 ) = − 1 − 1 − 0.5 = − 2.5 G_1 = -1 + 0.5 \times (-2) + 0.5^2 \times (-2) = -1 -1 -0.5 = -2.5 G1=−1+0.5×(−2)+0.52×(−2)=−1−1−0.5=−2.5。远处打折，是引入了不确定性。
  回报就是 "当前 + 未来所有奖励的打折总和"，用来衡量 "从这个状态出发，最终能拿到多少好处"。

import numpy as np
np.random.seed(0)
# 定义状态转移概率矩阵P
P = [
    [0.9, 0.1, 0.0, 0.0, 0.0, 0.0],
    [0.5, 0.0, 0.5, 0.0, 0.0, 0.0],
    [0.0, 0.0, 0.0, 0.6, 0.0, 0.4],
    [0.0, 0.0, 0.0, 0.0, 0.3, 0.7],
    [0.0, 0.2, 0.3, 0.5, 0.0, 0.0],
    [0.0, 0.0, 0.0, 0.0, 0.0, 1.0],
]
P = np.array(P)

rewards = [-1, -2, -2, 10, 1, 0]  # 定义奖励函数
gamma = 0.5  # 定义折扣因子


# 给定一条序列,计算从某个索引（起始状态）开始到序列最后（终止状态）得到的回报
def compute_return(start_index, chain, gamma):
    G = 0
    for i in reversed(range(start_index, len(chain))):
        G = gamma * G + rewards[chain[i] - 1]
    return G


# 一个状态序列,s1-s2-s3-s6
chain = [1, 2, 3, 6]
start_index = 0
G = compute_return(start_index, chain, gamma)
print("根据本序列计算得到回报为：%s。" % G)

根据本序列计算得到回报为：-2.5。

价值函数

在马尔可夫奖励过程中，一个状态的期望回报（即从这个状态出发的未来累积奖励的期望）被称为这个状态的价值 （value）。也就是我处于什么状态，未来积累的奖励期望我都是知道的，状态与积累奖励期望一一对应，就可以整理成函数关系了，那就是价值函数。

价值函数写成 V ( s ) = E G t ∣ S t = s V(s) = \mathbb{E}G_t \| S_t = s V(s)=EGt∣St=s，其中 G t = R t + γ R t + 1 + γ 2 R t + 2 + . . . G_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + ... Gt=Rt+γRt+1+γ2Rt+2+... 是 "未来累积奖励"，( γ \gamma γ 是 "折扣因子"，用来给未来奖励打折扣，比如未来的 100 分不如现在的 100 分值钱），s 就是状态。整理一下就是：
V ( s ) = E R t + γ R t + 1 + γ 2 R t + 2 + . . . ∣ S t = s V(s) = \mathbb{E}R_t + \\gamma R_{t+1} + \\gamma\^2 R_{t+2} + ... \| S_t = s V(s)=ERt+γRt+1+γ2Rt+2+...∣St=s上式再可以拆成 "现在的奖励" + "未来奖励的折扣期望"： V ( s ) = E R t ∣ S t = s + γ E R t + 1 + γ R t + 2 + . . . ∣ S t = s V(s) = \mathbb{E}R_t \| S_t = s + \gamma \mathbb{E}R_{t+1} + \\gamma R_{t+2} + ... \| S_t = s V(s)=ERt∣St=s+γERt+1+γRt+2+...∣St=s进一步简化， E R t ∣ S t = s \mathbb{E}R_t \| S_t = s ERt∣St=s 就是 r ( s ) r(s) r(s)， E R t + 1 + γ R t + 2 + . . . ∣ S t = s \mathbb{E}R_{t+1} + \\gamma R_{t+2} + ... \| S_t = s ERt+1+γRt+2+...∣St=s 其实是 "下一个状态 S t + 1 S_{t+1} St+1 的价值 V ( S t + 1 ) V(S_{t+1}) V(St+1) 的期望"（因为下一个状态的价值已经包含了它之后的所有奖励）。期望那就是要考虑概率了，而 "下一个状态的价值期望"，需要结合 "状态转移概率"（从 s 到其他状态 (s') 的概率 p ( s ′ ∣ s ) p(s'|s) p(s′∣s)）来算，所以： E V ( S t + 1 ) ∣ S t = s = ∑ s ′ ∈ S p ( s ′ ∣ s ) V ( s ′ ) \mathbb{E}V(S_{t+1}) \| S_t = s = \sum_{s' \in S} p(s'|s) V(s') EV(St+1)∣St=s=s′∈S∑p(s′∣s)V(s′)最终就得到了贝尔曼方程 ： V ( s ) = r ( s ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s ) V ( s ′ ) V(s) = r(s) + \gamma \sum_{s' \in S} p(s'|s) V(s') V(s)=r(s)+γs′∈S∑p(s′∣s)V(s′)翻译过来：当前状态的价值 = 现在的奖励 + 未来所有可能状态的价值 × 转移概率 × 折扣因子。

矩阵形式的贝尔曼方程如果有 n 个状态（比如游戏有 n 个关卡），把所有状态的 "价值" 写成向量 V \mathcal{V} V、"即时奖励" 写成向量 R \mathcal{R} R、"转移概率" 写成矩阵 P（矩阵里的 P ( s ′ ∣ s ) P(s'|s) P(s′∣s) 是从状态 s 到 s' 的概率），贝尔曼方程就可以写成矩阵乘法的形式： V = R + γ P V \mathcal{V} = \mathcal{R} + \gamma P \mathcal{V} V=R+γPV比如 n 个状态的例子：

V ( s 1 ) V ( s 2 ) . . . V ( s n ) = r ( s 1 ) r ( s 2 ) . . . r ( s n ) + γ p ( s 1 ∣ s 1 ) p ( s 2 ∣ s 1 ) . . . p ( s 3 ∣ s 1 ) p ( s 1 ∣ s 2 ) p ( s 2 ∣ s 2 ) . . . p ( s 3 ∣ s 2 ) . . . p ( s 1 ∣ s n ) p ( s 2 ∣ s n ) . . . p ( s n ∣ s n ) V ( s 1 ) V ( s 2 ) . . . V ( s n ) \begin{bmatrix} V(s_1) \\ V(s_2) \\...\\ V(s_n) \end{bmatrix}= \begin{bmatrix} r(s_1) \\ r(s_2) \\ ...\\r(s_n) \end{bmatrix}+ \gamma \begin{bmatrix} p(s_1|s_1) & p(s_2|s_1) &...& p(s_3|s_1) \\ p(s_1|s_2) & p(s_2|s_2) &...& p(s_3|s_2) \\ ... & \\ p(s_1|s_n) & p(s_2|s_n) &...& p(s_n|s_n) \end{bmatrix} \begin{bmatrix} V(s_1) \\ V(s_2) \\ ...\\ V(s_n) \end{bmatrix} V(s1)V(s2)...V(sn) = r(s1)r(s2)...r(sn) +γ p(s1∣s1)p(s1∣s2)...p(s1∣sn)p(s2∣s1)p(s2∣s2)p(s2∣sn).........p(s3∣s1)p(s3∣s2)p(sn∣sn) V(s1)V(s2)...V(sn)

进一步简化
V = R + γ P V \mathcal{V} = \mathcal{R} + \gamma P \mathcal{V} V=R+γPV ( I − γ P ) V = R (I- \gamma P)\mathcal{V} = \mathcal{R} (I−γP)V=R V = ( I − γ P ) − 1 R \mathcal{V} =(I- \gamma P)^{-1} \mathcal{R} V=(I−γP)−1R

贝尔曼方程是 "当前价值" 和 "未来价值" 的递推关系，用它可以计算每个状态的 "期望收益"。这个方法的计算复杂度是 O ( n 3 ) O(n^3) O(n3)（因为求矩阵逆的复杂度是 O ( n 3 ) O(n^3) O(n3)）。

接下来编写代码来实现求解价值函数的解析解方法，并据此计算该马尔可夫奖励过程中所有状态的价值。

def compute(P, rewards, gamma, states_num):
    ''' 利用贝尔曼方程的矩阵形式计算解析解,states_num是MRP的状态数 '''
    rewards = np.array(rewards).reshape((-1, 1))  #将rewards写成列向量形式
    value = np.dot(np.linalg.inv(np.eye(states_num, states_num) - gamma * P),
                   rewards)
    return value


V = compute(P, rewards, gamma, 6)
print("MRP中每个状态价值分别为\n", V)

MRP中每个状态价值分别为

\[-2.01950168

-2.21451846

1.16142785

10.53809283

3.58728554

0. \]

也就是

V ( s 1 ) V ( s 2 ) V ( s 3 ) V ( s 4 ) V ( s 5 ) V ( s 6 ) = − 2.02 − 2.21 1.16 10.54 3.59 0 \begin{bmatrix} V(s_1) \\ V(s_2) \\ V(s_3)\\ V(s_4)\\ V(s_5)\\ V(s_6) \end{bmatrix}= \begin{bmatrix} -2.02 \\ -2.21\\ 1.16\\10.54\\3.59\\0 \end{bmatrix} V(s1)V(s2)V(s3)V(s4)V(s5)V(s6) = −2.02−2.211.1610.543.590

马尔可夫决策过程

之前的马尔可夫过程（MP）、马尔可夫奖励过程（MRP）都是 "自发的随机过程"（比如小船随水流自己飘）；而 MDP 是在 MRP 基础上加入了智能体的 "动作"（比如水手控制小船的方向）------ 智能体可以主动选择动作，共同改变过程的走向。

• S（状态集合）所有可能的状态（比如小船在大海中的不同位置）
• A（动作集合）智能体可以选择的动作（比如小船的 "向左 / 向右 / 前进"）
• γ \gamma γ（折扣因子）对未来奖励的 "折现系数"（和 MRP 中作用一致，未来的奖励不如现在值钱）
• r ( s , a ) r(s,a) r(s,a)（奖励函数）奖励不仅和当前状态 s 有关，还和选择的动作 a 有关（比如 "在位置 s 选择向右，得到 + 5 奖励"）
• P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a)（状态转移函数）转移概率不仅和当前状态 s 有关，还和动作 a 有关（比如 "在位置 s 选择向右，转移到位置 s' 的概率是 0.8"）

MDP 比 MRP 多了 **"动作" 这个自变量 **：

• MRP 的转移、奖励只和 "状态" 有关（(P(s'|s)、r(s))）；
• MDP 的转移、奖励同时和 "状态 + 动作" 有关（(P(s'|s,a)、r(s,a))）。

MDP 用 "转移函数" 而非 MRP 的 "转移矩阵"，是因为动作的加入让转移变成了 "三维关系"，有限状态下可以用数组表示，无限状态下也能通过函数描述。

智能体与 MDP 环境的交互是一个循环过程：

• 智能体观察当前状态 S t S_t St；
• 从动作集合 A 中选一个动作 A t A_t At（这个选择规则叫 "策略"）；
• 环境根据 S t S_t St 和 A t A_t At，给出下一个状态 S t + 1 S_{t+1} St+1 和即时奖励 R t R_t Rt；
• 智能体重复上述步骤，目标是最大化累积奖励。

举个例子（小船的故事）MRP 场景 ：小船随水流飘，飘到目标点随机给奖励；
MDP 场景 ：水手（智能体）控制小船的方向（动作），不同方向（动作）对应不同的 "转移到目标点的概率" 和 "奖励"，水手需要选最优方向（策略）来尽可能多拿奖励。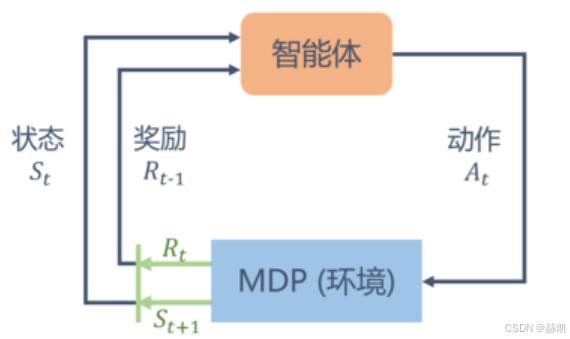

策略

策略（用 π \pi π表示）是智能体的 "决策规则" ：它描述 "在当前状态s下，选择某个动作a的概率"，公式为 π ( a ∣ s ) = P ( A t = a ∣ S t = s ) \pi(a|s) = P(A_t = a | S_t = s) π(a∣s)=P(At=a∣St=s)。

策略就是智能体 "在什么处境下，选什么动作" 的依据。

类型	特点	例子
确定性策略	每个状态下仅输出 1 个确定动作（该动作概率 = 1，其余 = 0）	游戏中 "血量 < 20% 时，必然选择吃药"
随机性策略	每个状态下输出动作的概率分布，再随机采样选动作	游戏中 "血量 < 20% 时，70% 概率吃药、30% 概率逃跑"

• 仅依赖当前状态：受马尔可夫性质约束，策略不需要考虑 "之前的状态 / 动作"，只看 "当前处境" 即可决策。
• 决定状态价值：不同策略会导致不同的动作选择，进而触发不同的状态转移和奖励，最终使得同一状态的 "长期期望奖励（价值）" 不同。

状态价值函数

状态价值函数 V π ( s ) V^\pi(s) Vπ(s) 是在遵循策略 π \pi π的前提下，从状态s出发能获得的 "长期期望奖励"。

简单来说：它衡量的是 "在当前状态s下，按照策略 π \pi π行动，未来能拿到的奖励总和的平均值"。

公式 V π ( s ) = E π G t ∣ S t = s V^\pi(s) = \mathbb{E}_\piG_t \| S_t = s Vπ(s)=EπGt∣St=s 中：

• E π ⋅ \mathbb{E}_\pi\\cdot Eπ⋅：表示 "遵循策略 π \pi π时的期望"（即平均结果）；
• G t G_t Gt：是从时刻t开始的 "未来累积奖励"（包含当前及后续所有奖励，通常带有折扣因子）；
• S t = s S_t = s St=s：表示 "当前处于状态s"。

动作价值函数

动作价值函数 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a) 是在遵循策略 π \pi π的前提下，"处于状态s且选择动作a" 时，能获得的长期期望奖励。简单说：它衡量的是 "在当前状态s下，选动作a这个选择好不好"------ 价值越高，说明这个 "状态 + 动作" 的组合能带来的长期收益越多。

公式 Q π ( s , a ) = E π G t ∣ S t = s , A t = a Q^\pi(s,a) = \mathbb{E}_\piG_t \| S_t = s, A_t = a Qπ(s,a)=EπGt∣St=s,At=a 中：

• E π ⋅ \mathbb{E}_\pi\\cdot Eπ⋅：遵循策略 π \pi π时的期望；
• G t G_t Gt：未来累积奖励；
• S t = s , A t = a S_t = s, A_t = a St=s,At=a：当前处于状态s且选择了动作a。

两者是 "整体与局部" 的关系，存在两层关联：

1. 状态价值是动作价值的 "加权和"
   状态s的价值 V π ( s ) V^\pi(s) Vπ(s)，等于 "在状态s下，按策略 π \pi π选每个动作的概率 π ( a ∣ s ) \pi(a|s) π(a∣s)，乘以该动作的价值 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a)，再把所有结果加起来"： V π ( s ) = ∑ a ∈ A π ( a ∣ s ) Q π ( s , a ) V^\pi(s) = \sum_{a \in A} \pi(a|s) Q^\pi(s,a) Vπ(s)=a∈A∑π(a∣s)Qπ(s,a)（比如状态s下，选动作a1的概率是 0.6、价值是 10；选a2的概率是 0.4、价值是 5，则状态s的价值是 0.6 × 10 + 0.4 × 5 = 8 ） 0.6×10 + 0.4×5 = 8） 0.6×10+0.4×5=8）
2. 动作价值是 "即时奖励 + 未来状态价值的期望"
   动作a的价值 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a)，等于 "当前选a的即时奖励 r ( s , a ) r(s,a) r(s,a)，加上折扣后所有下一个状态的价值期望"： Q π ( s , a ) = r ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ′ ) Q^\pi(s,a) = r(s,a) + \gamma \sum_{s' \in S} P(s'|s,a) V^\pi(s') Qπ(s,a)=r(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)（比如选动作a得到即时奖励 2，折扣 γ = 0.9 \gamma=0.9 γ=0.9；转移到状态s1的概率 0.7、价值 10，转移到s2的概率 0.3、价值 5，则动作a的价值是 2 + 0.9 × ( 0.7 × 10 + 0.3 × 5 ) = 2 + 0.9 × 8.5 = 9.65 2 + 0.9×(0.7×10 + 0.3×5) = 2 + 0.9×8.5 = 9.65 2+0.9×(0.7×10+0.3×5)=2+0.9×8.5=9.65）

状态价值函数 V π ( s ) V^\pi(s) Vπ(s)：衡量 "状态s的整体价值"；

动作价值函数 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a)：衡量 "状态s下选动作a的局部价值"。

贝尔曼期望方程

它是状态价值函数 / 动作价值函数的 "递推公式"------ 把当前状态（或动作）的价值，拆解为 "当前奖励" 和 "未来状态价值的期望" 之和，是强化学习中价值计算的核心公式。

状态价值的贝尔曼期望方程 推导与含义： V π ( s ) = E π R t + γ V π ( S t + 1 ) ∣ S t = s = ∑ a ∈ A π ( a ∣ s ) ( r ( s , a ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , a ) V π ( s ′ ) ) \begin{align*} V^\pi(s) &= \mathbb{E}\pi\leftR_t + \\gamma V\^\\pi(S_{t+1}) \\mid S_t = s\\right \\ &= \sum{a \in A} \pi(a|s) \left( r(s,a) + \gamma \sum_{s' \in S} p(s'|s,a) V^\pi(s') \right) \end{align*} Vπ(s)=EπRt+γVπ(St+1)∣St=s=a∈A∑π(a∣s)(r(s,a)+γs′∈S∑p(s′∣s,a)Vπ(s′))拆解为两层逻辑：

• 外层：按策略选动作的期望对状态s下所有可能的动作a，用 "选动作a的概率 π ( a ∣ s ) \pi(a|s) π(a∣s)" 加权求和；
• 内层：选动作a后的收益选动作a的收益 = 即时奖励 r ( s , a ) r(s,a) r(s,a) + 折扣后 "下一个状态的价值期望"（对所有可能的下一个状态 s ′ s' s′，用转移概率 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a)加权求和）。

动作价值的贝尔曼期望方程 推导与含义： Q π ( s , a ) = E π R t + γ Q π ( S t + 1 , A t + 1 ) ∣ S t = s , A t = a = r ( s , a ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , a ) ∑ a ′ ∈ A π ( a ′ ∣ s ′ ) Q π ( s ′ , a ′ ) \begin{align*} Q^\pi(s,a) &= \mathbb{E}\pi\leftR_t + \\gamma Q\^\\pi(S_{t+1}, A_{t+1}) \\mid S_t = s, A_t = a\\right \\ &= r(s,a) + \gamma \sum{s' \in S} p(s'|s,a) \sum_{a' \in A} \pi(a'|s') Q^\pi(s',a') \end{align*} Qπ(s,a)=EπRt+γQπ(St+1,At+1)∣St=s,At=a=r(s,a)+γs′∈S∑p(s′∣s,a)a′∈A∑π(a′∣s′)Qπ(s′,a′)拆解为两层逻辑：

• 当前部分：即时奖励选动作a的即时奖励 r ( s , a ) r(s,a) r(s,a)；
• 未来部分：下一个状态的动作价值期望先按转移概率 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a)转移到下一个状态 s ′ s' s′，再按策略 π \pi π选动作 a ′ a' a′，对 "下一个状态 + 动作" 的价值 Q π ( s ′ , a ′ ) Q^\pi(s',a') Qπ(s′,a′)加权求和，再乘以折扣因子 γ \gamma γ。

下图是一个马尔可夫决策过程的简单例子，其中每个深色圆圈代表一个状态，一共有从 s 1 ～ s 5 s_1 ～ s_5 s1～s5这 5个状态。黑色实线箭头代表可以采取的动作，浅色小圆圈代表动作，需要注意，并非在每个状态都能采取所有动作，例如在状态 s 1 s_1 s1，智能体只能采取"保持"和"前往"这两个动作，无法采取其他动作。

每个浅色小圆圈旁的数字代表在某个状态下采取某个动作能获得的奖励。虚线箭头代表采取动作后可能转移到的状态，箭头边上的数字代表转移概率，如果没有数字则表示转移概率为 1。例如，在 s 2 s_2 s2下， 如果采取动作"前往 s 3 s_3 s3"，就能得到奖励-2，并且转移到 s 3 s_3 s3；在 s 4 s_4 s4下，如果采取"概率前往"，就能得到奖励 1，并且会分别以概率0.2, 0.4, 0.4 转移到 s 2 s_2 s2 s 3 s_3 s3,或 s 4 s_4 s4。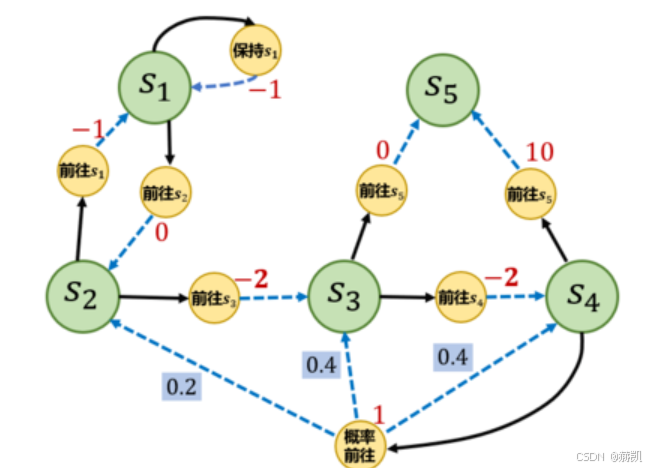

以状态 s 4 s_4 s4的 "概率前往" 动作为例：

• 即时奖励 r ( s 4 , 概率前往 ) = 1 r(s_4, \text{概率前往}) = 1 r(s4,概率前往)=1；
• 转移概率：到 s 2 s_2 s2（0.2）、 s 3 s_3 s3（0.4）、 s 4 s_4 s4（0.4）；
• 则该动作的价值 Q π ( s 4 , 概率前往 ) = 1 + γ × 0.2 V π ( s 2 ) + 0.4 V π ( s 3 ) + 0.4 V π ( s 4 ) Q^\pi(s_4, \text{概率前往}) = 1 + \gamma \times 0.2 V\^\\pi(s_2) + 0.4 V\^\\pi(s_3) + 0.4 V\^\\pi(s_4) Qπ(s4,概率前往)=1+γ×0.2Vπ(s2)+0.4Vπ(s3)+0.4Vπ(s4)。

S = ["s1", "s2", "s3", "s4", "s5"]  # 状态集合
A = ["保持s1", "前往s1", "前往s2", "前往s3", "前往s4", "前往s5", "概率前往"]  # 动作集合
# 状态转移函数
P = {
    "s1-保持s1-s1": 1.0,
    "s1-前往s2-s2": 1.0,
    "s2-前往s1-s1": 1.0,
    "s2-前往s3-s3": 1.0,
    "s3-前往s4-s4": 1.0,
    "s3-前往s5-s5": 1.0,
    "s4-前往s5-s5": 1.0,
    "s4-概率前往-s2": 0.2,
    "s4-概率前往-s3": 0.4,
    "s4-概率前往-s4": 0.4,
}
# 奖励函数
R = {
    "s1-保持s1": -1,
    "s1-前往s2": 0,
    "s2-前往s1": -1,
    "s2-前往s3": -2,
    "s3-前往s4": -2,
    "s3-前往s5": 0,
    "s4-前往s5": 10,
    "s4-概率前往": 1,
}
gamma = 0.5  # 折扣因子
MDP = (S, A, P, R, gamma)

# 策略1,随机策略
Pi_1 = {
    "s1-保持s1": 0.5,
    "s1-前往s2": 0.5,
    "s2-前往s1": 0.5,
    "s2-前往s3": 0.5,
    "s3-前往s4": 0.5,
    "s3-前往s5": 0.5,
    "s4-前往s5": 0.5,
    "s4-概率前往": 0.5,
}
# 策略2
Pi_2 = {
    "s1-保持s1": 0.6,
    "s1-前往s2": 0.4,
    "s2-前往s1": 0.3,
    "s2-前往s3": 0.7,
    "s3-前往s4": 0.5,
    "s3-前往s5": 0.5,
    "s4-前往s5": 0.1,
    "s4-概率前往": 0.9,
}


# 把输入的两个字符串通过"-"连接,便于使用上述定义的P、R变量
def join(str1, str2):
    return str1 + '-' + str2

状态s下，所有动作的 "（选这个动作的概率）×（这个动作的奖励）" 的总和，就是 MRP 里状态s的奖励

r ′ ( s ) = ∑ a ∈ A π ( a ∣ s ) r ( s , a ) r ′ (s)=∑ a∈A π(a∣s)r(s,a) r′(s)=∑a∈Aπ(a∣s)r(s,a)

状态s下，所有动作的 "（选这个动作的概率）×（这个动作下s转移到(s')的概率）" 的总和，就是 MRP 里状态s转移到(s')的概率。
P ′ ( s ′ ∣ s ) = ∑ a ∈ A π ( a ∣ s ) P ( s ′ ∣ s , a ) P ′ (s ′ ∣s)=∑ a∈A π(a∣s)P(s ′ ∣s,a) P′(s′∣s)=∑a∈Aπ(a∣s)P(s′∣s,a)

这样就能得到一个新的 MRP： ⟨ S , P ′ , r ′ , γ ⟩ \langle \mathcal{S}, P', r', \gamma \rangle ⟨S,P′,r′,γ⟩（和原 MDP 的状态空间、折扣因子一样）。而这个 MRP 的价值函数，正好等于原 MDP 里这个策略 π \pi π对应的状态价值函数。所以接下来只要用 MRP 算价值函数的方法（比如解析解），就能算出 MDP 里这个策略的状态价值了。

动作价值函数表示 "在状态s下采取动作a，后续遵循策略 π \pi π的期望回报"，公式为： Q π ( s , a ) = r ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ′ ) Q^\pi(s,a) = r(s,a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s,a) V_\pi(s') Qπ(s,a)=r(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)示例： ( s 4 , 概率前往 ) (s_4, 概率前往) (s4,概率前往)的动作价值计算代入数值： r ( s , a ) = 1 r(s,a)=1 r(s,a)=1， γ = 0.5 \gamma=0.5 γ=0.5，转移概率与对应状态价值的加权和为 0.2 × ( − 1.68 ) + 0.4 × 0.52 + 0.4 × 6.08 0.2×(-1.68)+0.4×0.52+0.4×6.08 0.2×(−1.68)+0.4×0.52+0.4×6.08，最终得到结果 2.152。

蒙特卡洛方法

蒙特卡洛方法（Monte-Carlo methods）也被称为统计模拟方法，是一种基于概率统计的数值计算方法。

圆的面积/方形的面积 = 圆里点的个数/方形里点的个数

用蒙特卡洛方法来估计一个策略在一个马尔可夫决策过程中的状态价值函数。

核心原理：用 "采样回报的均值" 近似 "期望回报"状态价值函数 V π ( s ) V^\pi(s) Vπ(s)的定义是 "从状态s出发、遵循策略 π \pi π的期望回报"。蒙特卡洛方法的直观思路是：通过策略 π \pi π在 MDP 中采样N条序列，计算每条序列中从状态s出发的回报 G t ( i ) G_t^{(i)} Gt(i)，再取这些回报的平均值，作为 V π ( s ) V^\pi(s) Vπ(s)的估计值： V π ( s ) = E π G t ∣ S t = s ≈ 1 N ∑ i = 1 N G t ( i ) V^\pi(s) = \mathbb{E}\piG_t\|S_t = s \approx \frac{1}{N} \sum{i=1}^N G_t^{(i)} Vπ(s)=EπGt∣St=s≈N1∑i=1NGt(i)

当用策略 π \pi π生成一条状态 - 奖励序列（比如 s 0 → r 0 s 1 → r 1 . . . → r T − 1 s T s_0 \xrightarrow{r^0} s_1 \xrightarrow{r^1} ... \xrightarrow{r^{T-1}} s_T s0r0 s1r1 ...rT−1 sT）时，同一个状态s可能：没出现过；只出现 1 次；出现多次。而这里的方法是：每条序列中，状态s第一次出现时，计算它的 "回报"（后续累积奖励）；后面再出现s，就忽略。

状态价值的计算步骤（基础版）我们要估算 "状态s的价值"（即从s出发，用策略 π \pi π能拿到的平均回报），步骤是：

1. 用策略 π \pi π生成很多条序列；
2. 对每条序列里的每个状态s（只看第一次出现的s）：给s的 "计数器" N ( s ) N(s) N(s)加 1（记录s被统计的次数）；把s对应的 "回报" G i G_i Gi（这条序列中s第一次出现后，后续所有奖励的累积和）加到s的 "总回报" M ( s ) M(s) M(s)里；
3. 状态s的价值 V ( s ) V(s) V(s) = 总回报 M ( s ) M(s) M(s) ÷ 次数 N ( s ) N(s) N(s)（即平均回报）。

增量更新版（更高效的计算方式）不用每次存 "总回报" 和 "次数"，可以实时更新价值：当状态s第 N ( s ) N(s) N(s)次被统计（此时 N ( s ) N(s) N(s)先 + 1），对应的回报是G，则新的价值为： V ( s ) ← V ( s ) + 1 N ( s ) × ( G − V ( s ) ) V(s) \leftarrow V(s) + \frac{1}{N(s)} \times \left( G - V(s) \right) V(s)←V(s)+N(s)1×(G−V(s))这个公式的意思是：用 "新回报G与当前价值 V ( s ) V(s) V(s)的差距"，按 1 N ( s ) \frac{1}{N(s)} N(s)1的比例调整价值（次数越多，单次调整的幅度越小）。总结核心逻辑是：通过 "多次采样序列→统计状态的平均回报"，来估算状态的价值；增量更新是更高效的实时计算方式，最终当采样次数足够多 ( N ( s ) → ∞ (N(s)\to\infty (N(s)→∞），估算的 V ( s ) V(s) V(s)会接近真实价值 V ∗ ( s ) V^*(s) V∗(s)。

来整个代码看看

def sample(MDP, Pi, timestep_max, number):
    ''' 采样函数,策略Pi,限制最长时间步timestep_max,总共采样序列数number '''
    S, A, P, R, gamma = MDP
    episodes = []
    for _ in range(number):
        episode = []
        timestep = 0
        s = S[np.random.randint(4)]  # 随机选择一个除s5以外的状态s作为起点
        # 当前状态为终止状态或者时间步太长时,一次采样结束
        while s != "s5" and timestep <= timestep_max:
            timestep += 1
            rand, temp = np.random.rand(), 0
            # 在状态s下根据策略选择动作
            for a_opt in A:
                temp += Pi.get(join(s, a_opt), 0)
                if temp > rand:
                    a = a_opt
                    r = R.get(join(s, a), 0)
                    break
            rand, temp = np.random.rand(), 0
            # 根据状态转移概率得到下一个状态s_next
            for s_opt in S:
                temp += P.get(join(join(s, a), s_opt), 0)
                if temp > rand:
                    s_next = s_opt
                    break
            episode.append((s, a, r, s_next))  # 把（s,a,r,s_next）元组放入序列中
            s = s_next  # s_next变成当前状态,开始接下来的循环
        episodes.append(episode)
    return episodes


# 采样5次,每个序列最长不超过20步
episodes = sample(MDP, Pi_1, 20, 5)
print('第一条序列\n', episodes[0])
print('第二条序列\n', episodes[1])
print('第五条序列\n', episodes[4])

第一条序列

('s1', '前往s2', 0, 's2'), ('s2', '前往s3', -2, 's3'), ('s3', '前往s5', 0, 's5')

第二条序列

('s4', '概率前往', 1, 's4'), ('s4', '前往s5', 10, 's5')

第五条序列

('s2', '前往s3', -2, 's3'), ('s3', '前往s4', -2, 's4'), ('s4', '前往s5', 10, 's5')

# 对所有采样序列计算所有状态的价值
def MC(episodes, V, N, gamma):
    for episode in episodes:
        G = 0
        for i in range(len(episode) - 1, -1, -1):  #一个序列从后往前计算
            (s, a, r, s_next) = episode[i]
            G = r + gamma * G
            N[s] = N[s] + 1
            V[s] = V[s] + (G - V[s]) / N[s]


timestep_max = 20
# 采样1000次,可以自行修改
episodes = sample(MDP, Pi_1, timestep_max, 1000)
gamma = 0.5
V = {"s1": 0, "s2": 0, "s3": 0, "s4": 0, "s5": 0}
N = {"s1": 0, "s2": 0, "s3": 0, "s4": 0, "s5": 0}
MC(episodes, V, N, gamma)
print("使用蒙特卡洛方法计算MDP的状态价值为\n", V)

使用蒙特卡洛方法计算MDP的状态价值为

{'s1': -1.228923788722258, 's2': -1.6955696284402704, 's3': 0.4823809701532294, 's4': 5.967514743019431, 's5': 0}

比较接近。

占有度量

不同策略会让智能体访问状态的概率分布不同：比如某策略让智能体快速到达终止态，就会很少访问其他状态，这会直接影响策略的价值函数。因此需要用 "占用度量" 量化这种访问频率。

定义：策略 π \pi π下，状态s被访问的长期归一化频率，公式为： v π ( s ) = ( 1 − γ ) ∑ t = 0 ∞ γ t P t π ( s ) v^\pi(s) = (1-\gamma) \sum_{t=0}^\infty \gamma^t P_t^\pi(s) vπ(s)=(1−γ)t=0∑∞γtPtπ(s)其中：

• P t π ( s ) P_t^\pi(s) Ptπ(s)是 "策略 π \pi π下，时刻t处于状态s的概率"，初始时 P 0 π ( s ) P_0^\pi(s) P0π(s)等于初始状态分布 ν ( s ) \nu(s) ν(s)；
• ( 1 − γ ) (1-\gamma) (1−γ)是归一化因子，保证所有状态的访问频率之和为 1；
• γ \gamma γ是折扣因子，体现 "近期状态的权重更高"。

性质：状态访问频率满足递归关系： v π ( s ′ ) = ( 1 − γ ) ν ( s ′ ) + γ ∫ P ( s ′ ∣ s , a ) π ( a ∣ s ) v π ( s ) d s d a v^\pi(s') = (1-\gamma)\nu(s') + \gamma \int P(s'|s,a)\pi(a|s)v^\pi(s)dsda vπ(s′)=(1−γ)ν(s′)+γ∫P(s′∣s,a)π(a∣s)vπ(s)dsda含义是：状态 s ′ s' s′的访问频率 = 初始分布中 s ′ s' s′的占比 + 从其他状态通过 "动作 - 转移" 到达 s ′ s' s′的频率的折扣和。

占用度量 ( ρ π ( s , a ) (\rho^\pi(s,a) (ρπ(s,a)）定义：策略 π \pi π下，"状态s+ 动作a" 这个状态 - 动作对被访问的长期归一化频率，公式为： ρ π ( s , a ) = ( 1 − γ ) ∑ t = 0 ∞ γ t P t π ( s ) π ( a ∣ s ) \rho^\pi(s,a) = (1-\gamma) \sum_{t=0}^\infty \gamma^t P_t^\pi(s)\pi(a|s) ρπ(s,a)=(1−γ)t=0∑∞γtPtπ(s)π(a∣s)与状态访问频率的关系： ρ π ( s , a ) = v π ( s ) π ( a ∣ s ) \rho^\pi(s,a) = v^\pi(s)\pi(a|s) ρπ(s,a)=vπ(s)π(a∣s)含义是："状态s选动作a" 的频率 = 状态s的访问频率 × 策略 π \pi π在s下选a的概率。

两个核心定理（策略与占用度量的一一对应）
定理 1 ：若两个策略 π 1 \pi_1 π1和 π 2 \pi_2 π2对应的占用度量相同 ( ρ π 1 = ρ π 2 (\rho^{\pi_1} = \rho^{\pi_2} (ρπ1=ρπ2），则这两个策略完全一致（ π 1 = π 2 \pi_1 = \pi_2 π1=π2）。
定理 2 ：给定一个 "合法" 的占用度量 ρ \rho ρ（即存在策略能产生的 ρ \rho ρ），对应的唯一策略为： π ρ ( a ∣ s ) = ρ ( s , a ) ∑ a ′ ρ ( s , a ′ ) \pi_\rho(a|s) = \frac{\rho(s,a)}{\sum_{a'} \rho(s,a')} πρ(a∣s)=∑a′ρ(s,a′)ρ(s,a)含义是：策略在s下选a的概率，等于 "s+a" 的频率占 "s下所有动作频率之和" 的比例。

总结占用度量的核心作用是用 "状态 / 动作的访问频率" 来唯一表征策略，后续可通过估计访问频率来间接分析或优化策略。

def occupancy(episodes, s, a, timestep_max, gamma):
    ''' 计算状态动作对（s,a）出现的频率,以此来估算策略的占用度量 '''
    rho = 0
    total_times = np.zeros(timestep_max)  # 记录每个时间步t各被经历过几次
    occur_times = np.zeros(timestep_max)  # 记录(s_t,a_t)=(s,a)的次数
    for episode in episodes:
        for i in range(len(episode)):
            (s_opt, a_opt, r, s_next) = episode[i]
            total_times[i] += 1
            if s == s_opt and a == a_opt:
                occur_times[i] += 1
    for i in reversed(range(timestep_max)):
        if total_times[i]:
            rho += gamma**i * occur_times[i] / total_times[i]
    return (1 - gamma) * rho


gamma = 0.5
timestep_max = 1000

episodes_1 = sample(MDP, Pi_1, timestep_max, 1000)
episodes_2 = sample(MDP, Pi_2, timestep_max, 1000)
rho_1 = occupancy(episodes_1, "s4", "概率前往", timestep_max, gamma)
rho_2 = occupancy(episodes_2, "s4", "概率前往", timestep_max, gamma)
print(rho_1, rho_2)

0.112567796310472 0.23199480615618912

最优策略

强化学习的目标是找一个策略 π ∗ \pi^* π∗，让智能体从初始状态出发拿到最大的期望回报。策略之间的 "好坏" 是这么比的：如果策略 π \pi π在所有状态s下的价值都≥策略 π ′ \pi' π′的价值（即 V π ( s ) ≥ V π ′ ( s ) , ∀ s V^\pi(s) \geq V^{\pi'}(s), \forall s Vπ(s)≥Vπ′(s),∀s），就说 π \pi π比 π ′ \pi' π′好（记 π > π ′ \pi > \pi' π>π′）。

在有限状态 / 动作的 MDP 中，至少存在一个 "最优策略"：它不比任何其他策略差（甚至比所有策略都好）。最优策略可能有多个，统一记为 π ∗ ( s ) \pi^*(s) π∗(s)。

所有最优策略对应的 "状态价值函数" 是完全一样的，这个函数叫最优状态价值函数，定义是： V ∗ ( s ) = max ⁡ π V π ( s ) , ∀ s ∈ S V^*(s) = \max_\pi V^\pi(s), \quad \forall s \in S V∗(s)=maxπVπ(s),∀s∈S。状态s的最优价值，是 "所有可能策略下s的价值" 里的最大值。

类似地，最优动作价值函数是 "所有策略下动作价值" 的最大值： Q ∗ ( s , a ) = max ⁡ π Q π ( s , a ) , ∀ s ∈ S , a ∈ A Q^*(s,a) = \max_\pi Q^\pi(s,a), \quad \forall s \in S, a \in \mathcal{A} Q∗(s,a)=maxπQπ(s,a),∀s∈S,a∈A。在状态s选动作a后，后续用最优策略能拿到的最大期望回报。

最优动作价值和最优状态价值是相互关联的：从动作价值到状态价值：状态s的最优价值，是 "s下所有动作的最优动作价值" 里的最大值（选最好的动作）： V ∗ ( s ) = max ⁡ a ∈ A Q ∗ ( s , a ) V^*(s) = \max_{a \in \mathcal{A}} Q^*(s,a) V∗(s)=maxa∈AQ∗(s,a)，从状态价值到动作价值：动作 ( s , a ) (s,a) (s,a)的最优价值 = 当前奖励 r ( s , a ) r(s,a) r(s,a) + 后续所有状态的最优价值的 "折扣期望"（后续用最优策略）： Q ∗ ( s , a ) = r ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V ∗ ( s ′ ) Q^*(s,a) = r(s,a) + \gamma \sum_{s' \in S} P(s'|s,a) V^*(s') Q∗(s,a)=r(s,a)+γ∑s′∈SP(s′∣s,a)V∗(s′)

总结核心逻辑是：最优策略对应 "最优的状态 / 动作价值"，而这两个价值函数通过 "选最优动作 + 后续最优策略" 相互推导。

贝尔曼最优方程

状态价值的贝尔曼最优方程公式

V ∗ ( s ) = max ⁡ a ∈ A { r ( s , a ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , a ) V ∗ ( s ′ ) } V^*(s) = \max_{a \in \mathcal{A}} \left\{ r(s,a) + \gamma \sum_{s' \in S} p(s'|s,a) V^*(s') \right\} V∗(s)=maxa∈A{r(s,a)+γ∑s′∈Sp(s′∣s,a)V∗(s′)}

含义：状态s的最优价值，等于 "选择当前最优动作a后，立即获得的奖励(r(s,a))，加上后续所有可能转移状态(s')的最优价值的折扣期望" 的最大值。（本质是 "选最优动作 + 后续最优策略" 的价值总和）

动作价值的贝尔曼最优方程公式

( Q ∗ ( s , a ) = r ( s , a ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , a ) max ⁡ a ′ ∈ A Q ∗ ( s ′ , a ′ ) (Q^*(s,a) = r(s,a) + \gamma \sum_{s' \in S} p(s'|s,a) \max_{a' \in \mathcal{A}} Q^*(s',a') (Q∗(s,a)=r(s,a)+γ∑s′∈Sp(s′∣s,a)maxa′∈AQ∗(s′,a′)

含义：动作 ( s , a ) (s,a) (s,a)的最优价值，等于 "当前奖励 r ( s , a ) r(s,a) r(s,a)，加上后续转移状态 s ′ s' s′下最优动作价值的折扣期望"。

（本质是 "执行动作a的奖励 + 后续状态选最优动作的价值总和"）

贝尔曼最优方程的作用它是求解 "最优状态 / 动作价值" 的数学基础，后续（如动态规划）会通过迭代求解该方程，得到最优策略对应的价值函数。