1. 树的基本定义
树是一个或多个节点的有限集合,满足以下条件:
- 存在一个特定的节点,称为根节点;
- 其余节点被划分为
n个互不相交的子集(记为T₁, T₂, ..., Tₙ),每个子集本身都是一棵树,称为根节点的子树。
2. 树的核心术语
2.1 节点相关术语
- 节点:树中的独立单元
- 节点的度:节点拥有的子树数量
- 树的度:树内所有节点度的最大值
- 叶子节点:度为 0 的节点
- 非终端节点:度不为 0 的节点
2.2 关系与层次术语
- 双亲和孩子 :节点的子树根称为该节点的孩子 ,该节点称为孩子的双亲
- 层次:从根开始定义,根为第 1 层,根的孩子为第 2 层,以此类推
3. 树的基本性质
3.1 性质一
树中所有节点数 = 所有节点的度数之和 + 1(根节点无父节点)
3.2 性质二
对于度为 m 的树,第 i 层上最多有 m^(i-1) 个节点。
3.3 性质三
对于高度为 h、度为 m 的树,最多有 (m^h - 1)/(m - 1) 个节点(满 m 叉树)。
4. 二叉树的基本定义
二叉树是 n(n≥0) 个节点的集合,满足:
- 空树(
n=0)或非空树; - 非空树有且仅有一个根节点;
- 其余节点分为两个互不相交的子集(左子树 和右子树),且左、右子树本身也是二叉树;
- 每个节点至多有 2 棵子树;
- 子树有左右之分,次序不能颠倒。
5. 二叉树的基本形态
- 空二叉树;
- 仅有根节点;
- 根节点仅有左子树;
- 根节点仅有右子树;
- 根节点的左右子树均非空。
6. 二叉树的性质
6.1 性质一
二叉树的第 i 层最多有 2^(i-1) 个节点(i≥1)。
6.2 性质二
深度为 k 的二叉树最多有 2^k - 1 个节点(k≥1)。
6.3 性质三
对于任何非空二叉树 T,若叶子节点数为 n₀、度为 2 的节点数为 n₂,则 n₀ = n₂ + 1。
7. 特殊二叉树
7.1 满二叉树
- 定义:深度为
k且含有2^k - 1个节点的二叉树; - 特点:所有叶子节点仅出现在最后一层;
- 编号规则:根节点从 1 开始,从上到下、从左到右编号,编号为
i的节点,左孩子编号为2i,右孩子编号为2i+1。
7.2 完全二叉树
7.2.1 完全二叉树的定义
深度为k、有n个节点的二叉树,当且仅当其每个节点都与深度为k的满二叉树中编号 1 至n的节点一一对应时,称为完全二叉树。
7.2.2 完全二叉树的核心特点
- 叶子节点仅可能出现在层次最大的两层;
- 对任一节点,若其右分支子孙的最大层次为
l,则左分支子孙的最大层次必为l或l+1; - 约束规则:无左子树则不能有右子树;上一层未铺满则不能有下一层。
7.2.3 完全二叉树的性质
- 性质四 :有
n个节点的完全二叉树,深度为⌊log₂n⌋ + 1(⌊⌋表示向下取整); - 性质五 (层序编号规则):对编号为
i(1≤i≤n)的节点:- 若
i=1,则为根节点,无双亲;若i>1,双亲为⌊i/2⌋; - 若
2i > n,则无左孩子(为叶子节点);否则左孩子为2i; - 若
2i+1 > n,则无右孩子;否则右孩子为2i+1。
- 若
7.2.4 完全二叉树真题解析
- 题 1(2009) :第 6 层有 8 个叶节点的完全二叉树,节点数最多为
111(前 6 层满二叉树共 63 个节点,第 7 层最多有24×2=48个节点,总计63+48=111); - 题 2(2011) :768 个节点的完全二叉树,叶节点数为
384(利用n = n₀ + n₁ + n₂和n₀ = n₂+1,结合节点数为偶数时n₁=1,计算得n₀=384)。
7.3 斜树
所有节点都只有左子树(左斜树)或只有右子树(右斜树)的二叉树,结构类似线性表。
7.4 二叉排序树 / 二叉搜索树
左子树节点值 ≤ 根节点值 ≤ 右子树节点值的二叉树,支持高效的查找、插入、删除操作。
8. 二叉树的存储结构
8.1 链式存储结构
通过节点结构体存储数据、左孩子指针、右孩子指针,这是二叉树最常用的存储方式,能灵活表示任意形态的二叉树。
cs
typedef char ElemType;
typedef struct TreeNode
{
ElemType data; // 节点存储的数据
struct TreeNode *lchild; // 指向左孩子的指针
struct TreeNode *rchild; // 指向右孩子的指针
}TreeNode;
typedef TreeNode* BiTree; // 定义二叉树类型,本质是指向根节点的指针8.2 顺序存储结构(补充)
利用数组存储二叉树节点,节点的下标对应其在满二叉树中的编号,通过下标计算来确定节点的双亲、孩子关系。
- 优点:访问节点的双亲 / 孩子速度快;
- 缺点:对非完全二叉树会造成空间浪费(需按满二叉树的节点数分配数组)。
9. 二叉树的遍历
9.1 前序遍历
9.1.1 遍历规则
遍历顺序:根节点 → 左子树 → 右子树,即先访问根节点,再递归遍历左子树,最后递归遍历右子树。
9.1.2 递归代码
cs
void preOrder(BiTree T)
{
if (T == NULL) return; // 递归终止条件:空树直接返回
printf("%c ", T->data); // 访问根节点的数据
preOrder(T->lchild); // 递归遍历左子树
preOrder(T->rchild); // 递归遍历右子树
}9.1.3 非递归前序遍历(借助栈)
通过栈模拟递归过程,实现前序遍历的非递归版本:
cs
// 假设栈的基础操作(push、pop、isEmpty)已实现
void iterPreOrder(Stack *s, BiTree T)
{
while (T != NULL || isEmpty(s) != 0)
{
// 遍历左子树,同时访问根节点并入栈
while (T != NULL)
{
printf("%c ", T->data); // 访问根节点
push(s, T); // 节点入栈
T = T->lchild; // 移动到左子树
}
// 左子树遍历完成,弹出栈顶节点,转向右子树
pop(s, &T);
T = T->rchild;
}
}9.2 中序遍历
9.2.1 遍历规则
遍历顺序:左子树 → 根节点 → 右子树,即先递归遍历左子树,再访问根节点,最后递归遍历右子树。
9.2.2 代码
cs
void inOrder(BiTree T)
{
if (T == NULL) return; // 递归终止条件:空树直接返回
inOrder(T->lchild); // 递归遍历左子树
printf("%c ", T->data); // 访问根节点的数据
inOrder(T->rchild); // 递归遍历右子树
}9.3 后序遍历
9.3.1 遍历规则
遍历顺序:左子树 → 右子树 → 根节点,即先递归遍历左子树,再递归遍历右子树,最后访问根节点。
9.3.2 代码
cs
void postOrder(BiTree T)
{
if (T == NULL) return; // 递归终止条件:空树直接返回
postOrder(T->lchild); // 递归遍历左子树
postOrder(T->rchild); // 递归遍历右子树
printf("%c ", T->data); // 访问根节点的数据
}9.4 层序遍历
9.4.1 遍历规则
按层次从上到下、同一层从左到右依次访问节点,需要借助队列实现非递归遍历。
9.4.2 代码(借助队列)
cs
#include <stdio.h>
#include <stdlib.h>
// 队列节点结构(用于层序遍历)
typedef struct QueueNode {
BiTree data;
struct QueueNode *next;
} QueueNode;
typedef struct {
QueueNode *front; // 队头指针
QueueNode *rear; // 队尾指针
} LinkQueue;
// 初始化队列
void initQueue(LinkQueue *Q) {
Q->front = Q->rear = (QueueNode*)malloc(sizeof(QueueNode));
Q->front->next = NULL;
}
// 入队
void enQueue(LinkQueue *Q, BiTree t) {
QueueNode *p = (QueueNode*)malloc(sizeof(QueueNode));
p->data = t;
p->next = NULL;
Q->rear->next = p;
Q->rear = p;
}
// 出队
int deQueue(LinkQueue *Q, BiTree *t) {
if (Q->front == Q->rear) return 0; // 空队列
QueueNode *p = Q->front->next;
*t = p->data;
Q->front->next = p->next;
if (Q->rear == p) Q->rear = Q->front;
free(p);
return 1;
}
// 层序遍历
void levelOrder(BiTree T) {
LinkQueue Q;
initQueue(&Q);
BiTree p;
enQueue(&Q, T); // 根节点入队
while (deQueue(&Q, &p)) { // 队列非空时循环
printf("%c ", p->data); // 访问当前节点
if (p->lchild) enQueue(&Q, p->lchild); // 左孩子入队
if (p->rchild) enQueue(&Q, p->rchild); // 右孩子入队
}
}总结
- 树的核心定义围绕根节点和子树的层级关系,二叉树是每个节点最多有两个子树的特殊树结构。
- 完全二叉树有明确的编号规则和层次性质,是实现堆结构的基础。
- 二叉树的遍历有前序、中序、后序(递归为主)和层序(借助队列)四种方式,不同遍历顺序对应不同的访问逻辑。
9.5 遍历序列的性质
已知不同遍历序列的组合,对二叉树的唯一确定性有以下规则:
- 已知前序 + 中序:可唯一确定一棵二叉树;
- 已知中序 + 后序:可唯一确定一棵二叉树;
- 已知前序 + 后序 :不能唯一确定一棵二叉树(无法区分左右子树的范围)。
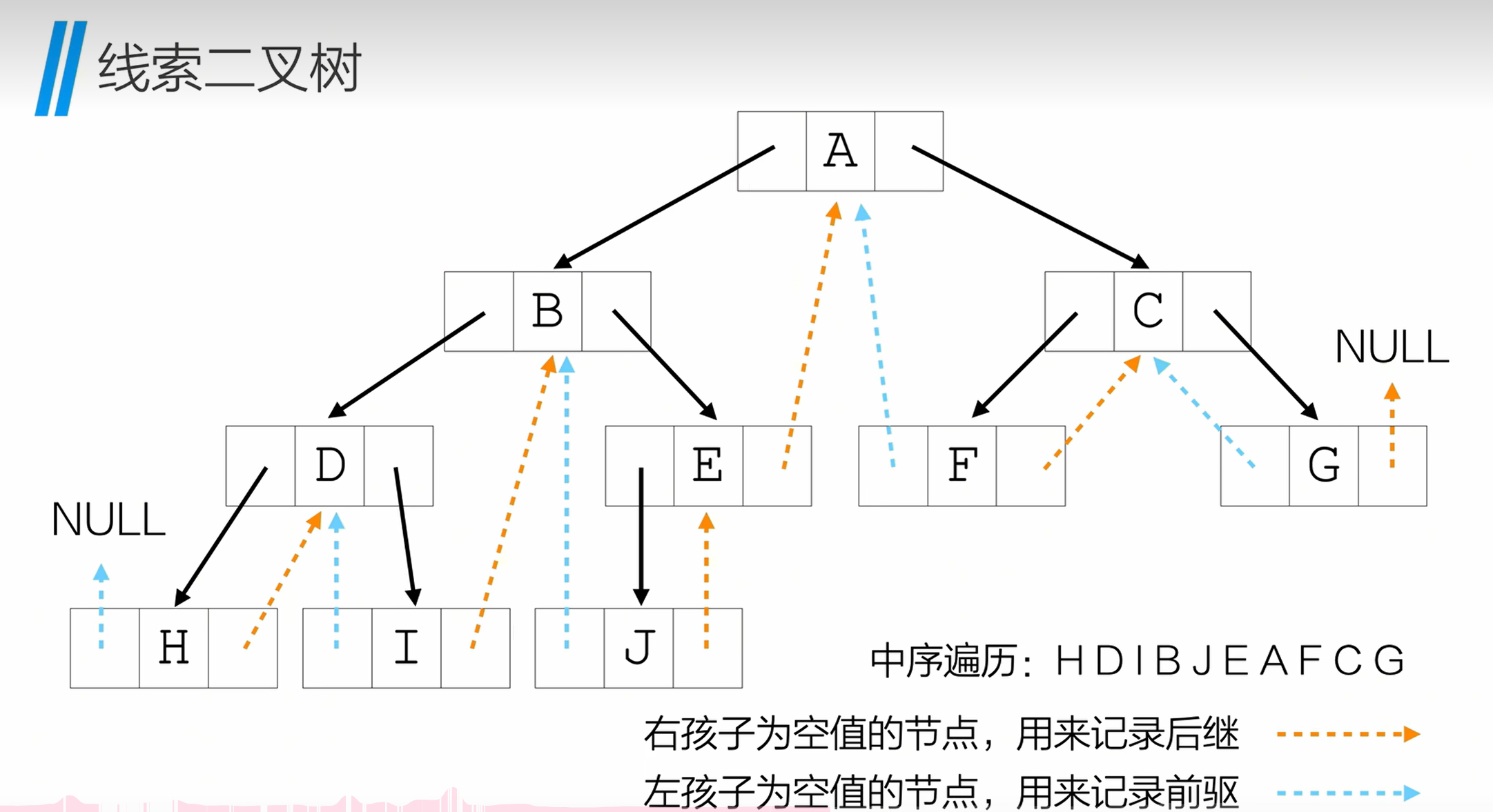
10. 线索二叉树
10.1 线索二叉树的定义与作用
- 背景:普通二叉树的空指针(叶节点的左右孩子)存在空间浪费,且遍历后才能得到节点的前驱 / 后继关系;
- 线索化:利用叶节点的空指针,记录节点在某一遍历序列 中的前驱 (左空指针)和后继(右空指针);
- 作用:无需递归 / 栈,直接通过线索快速遍历二叉树,提高遍历效率。
10.2 线索二叉树的存储结构
在普通二叉树节点基础上,增加ltag和rtag标记指针类型:
cs
typedef char ElemType;
typedef struct ThreadNode
{
ElemType data; // 节点数据
struct ThreadNode *lchild; // 左指针(孩子/前驱)
struct ThreadNode *rchild; // 右指针(孩子/后继)
int ltag; // 0=左孩子,1=前驱线索
int rtag; // 0=右孩子,1=后继线索
}ThreadNode;
typedef ThreadNode* ThreadTree; // 线索二叉树类型10.3 中序遍历线索化的实现
以中序遍历为例,线索化后需添加头结点形成循环链表,规则:
- 头结点的
lchild指向二叉树根节点,rchild指向中序遍历的最后一个节点; - 中序遍历的第一个节点的
lchild指向头结点; - 中序遍历的最后一个节点的
rchild指向头结点。 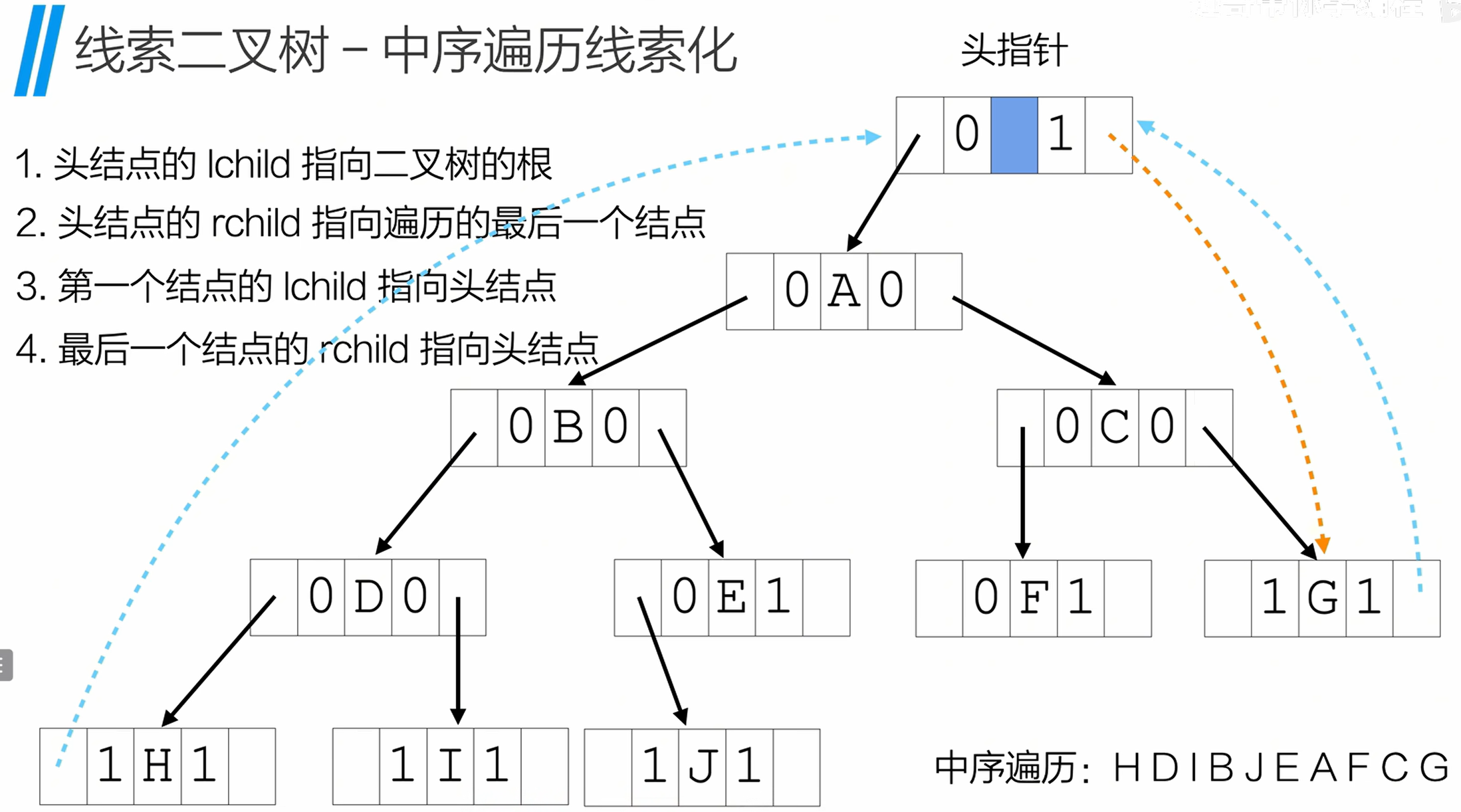
10.4 线索二叉树的操作流程
cs
int main(int argc, char const *argv[])
{
ThreadTree head; // 线索二叉树的头结点
ThreadTree T; // 普通二叉树的根节点
// 1. 创建普通二叉树
createTree(&T);
// 2. 对普通二叉树进行中序线索化
inOrderThreading(&head, T);
// 3. 基于线索遍历线索二叉树
inOrder(head);
return 0;
}11. 哈夫曼树与哈夫曼编码
11.1 哈夫曼树的基本概念
11.1.1 核心术语
- 路径:树中一个节点到另一个节点的分支序列;
- 路径长度:路径上的分支数目;
- 树的路径长度:从根到所有节点的路径长度之和;
- 节点的权:给节点赋予的有意义数值
- 节点的带权路径长度:节点的权 × 从根到该节点的路径长度;
- 树的带权路径长度(WPL):所有叶节点的带权路径长度之和。
11.2 哈夫曼树的定义
哈夫曼树是树的带权路径长度(WPL)最小的二叉树(也称为最优二叉树)。
11.3 哈夫曼树的构造步骤
以权值为5(不及格)、10(优秀)、15(及格)、30(良好)、40(中等)的叶节点为例:
- 排序叶节点:将叶节点按权值从小到大排序,得到序列:5、10、15、30、40;
- 合并最小权值节点 :取权值最小的两个节点(5、10),作为新节点
N₁的子节点,N₁的权值为5+10=15; - 更新有序序列 :用
N₁替换取出的两个节点,新序列为:15(N₁)、15(及格)、30(良好)、40(中等); - 重复合并与更新 :
- 取当前最小的两个节点(15、15),合并为新节点
N₂(权值 30),更新序列为:30(N₂)、30(良好)、40(中等); - 取 30、30,合并为新节点
N₃(权值 60),更新序列为:40(中等)、60(N₃); - 取 40、60,合并为新节点
N₄(权值 100),最终得到哈夫曼树。 



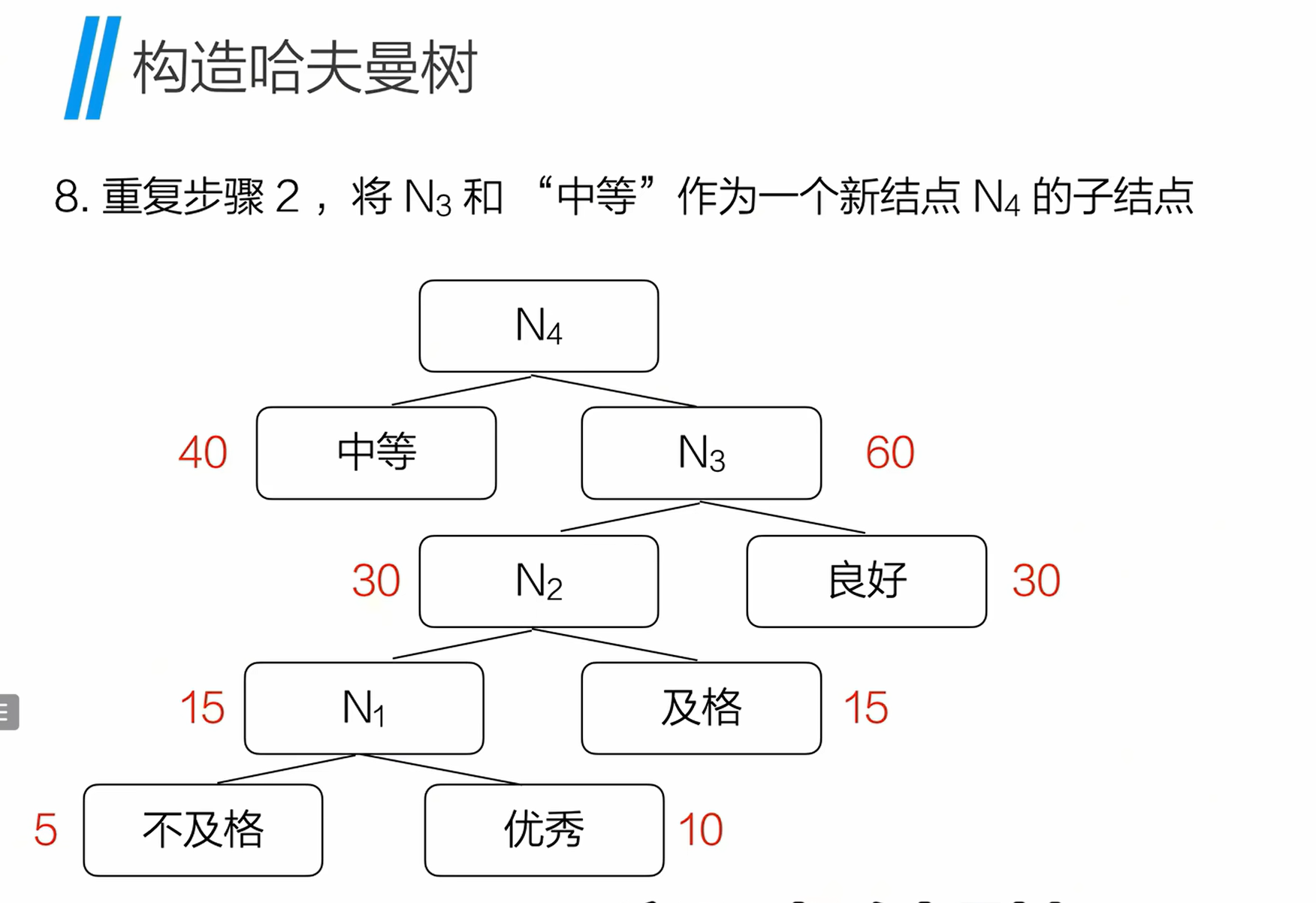
- 取当前最小的两个节点(15、15),合并为新节点
11.4 哈夫曼编码
11.4.1 编码背景
用于解决数据传输的优化问题:通过变长编码(权值大的节点编码更短)减少总传输长度。
11.4.2 编码规则
以哈夫曼树为基础,从根节点出发:
- 左子树路径标记为 "0",右子树路径标记为 "1";
- 叶节点的路径序列即为其哈夫曼编码。
11.4.4 哈夫曼编码的核心特点
哈夫曼编码是无歧义的最短变长编码:
- 无歧义:编码为 "前缀码"(任一字符的编码不是其他字符编码的前缀),避免解码时的歧义;
- 最短:通过哈夫曼树的带权路径最优性,实现总编码长度最短。
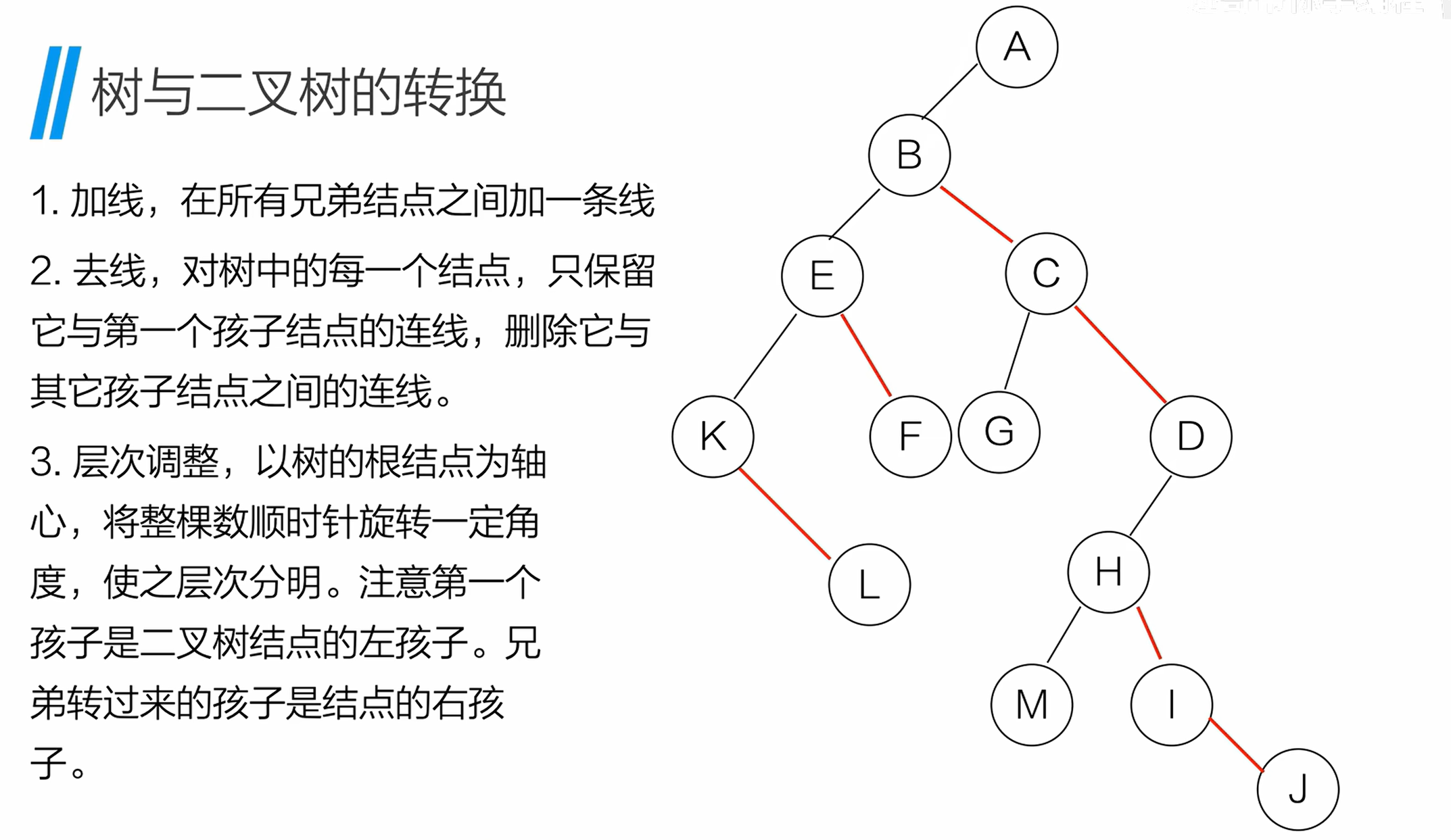
12. 树与二叉树的转换
12.1 树转二叉树的步骤
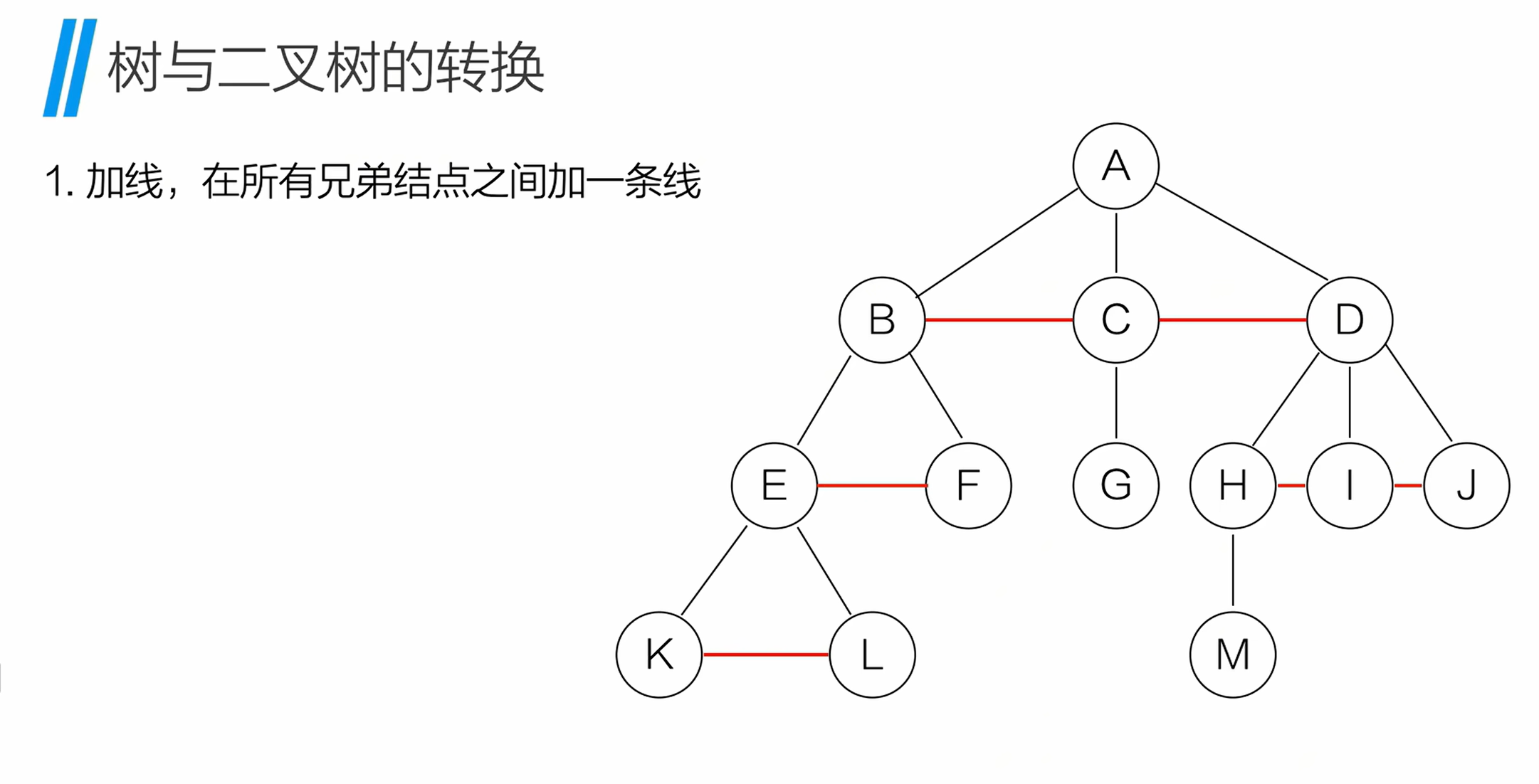
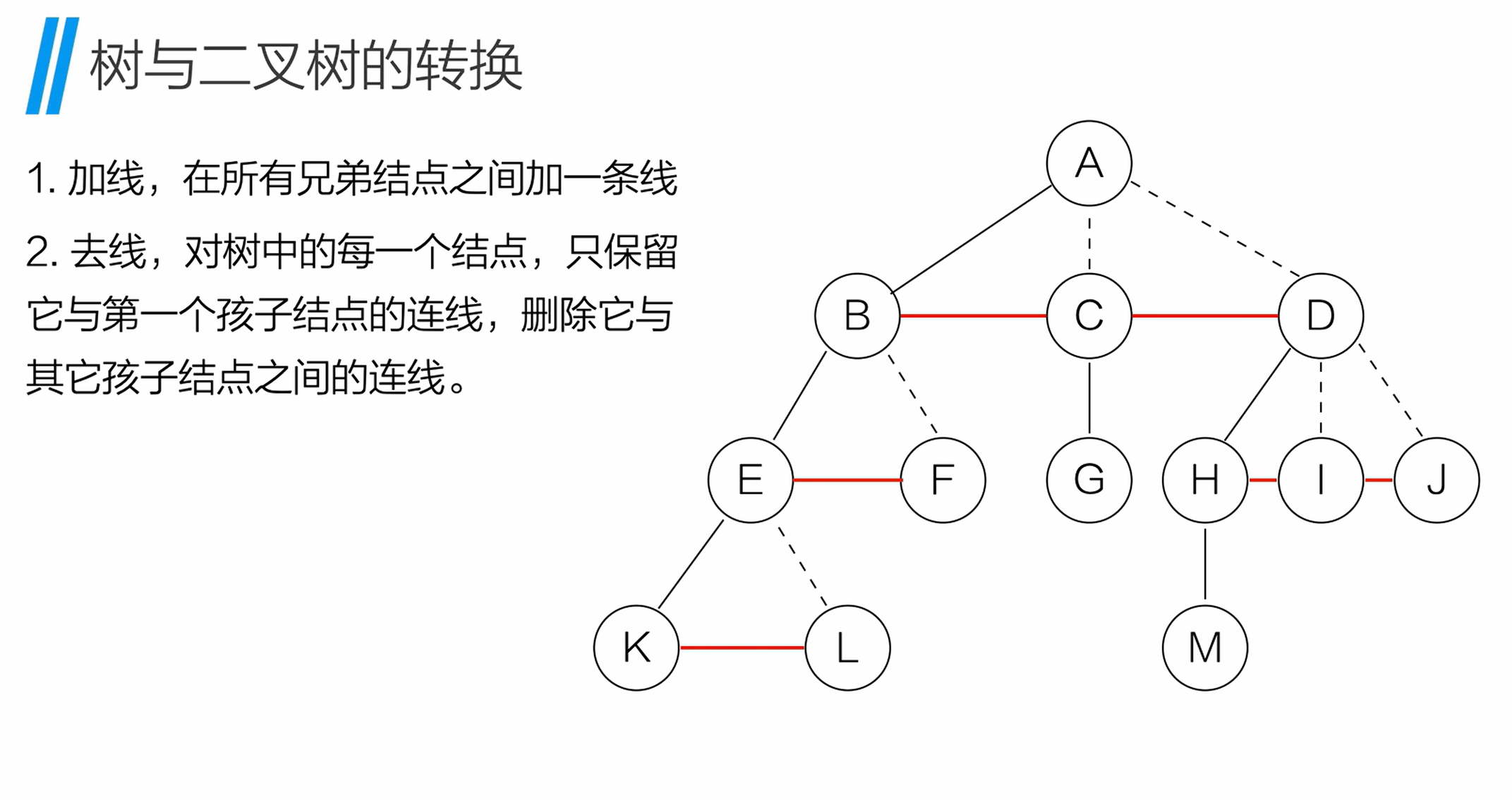
将普通树(多叉树)转换为二叉树,遵循 "左孩子,右兄弟" 规则:
- 加线:在所有兄弟节点之间添加一条连线;
- 去线 :对每个节点,仅保留与第一个孩子的连线,删除与其他孩子的连线;
- 层次调整:以根节点为轴心,顺时针旋转树,使 "第一个孩子" 成为二叉树的左孩子,"兄弟节点" 成为右孩子。
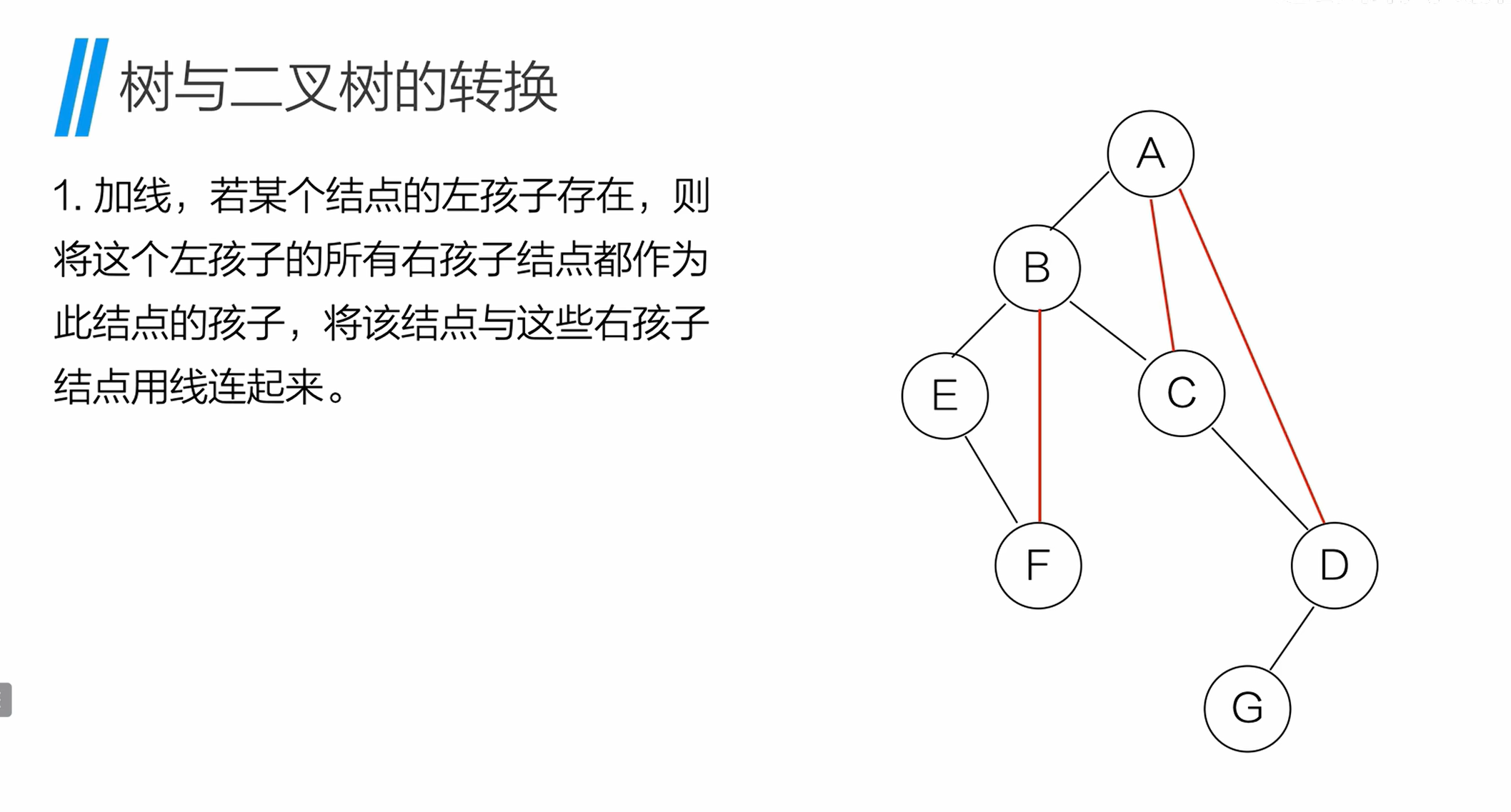
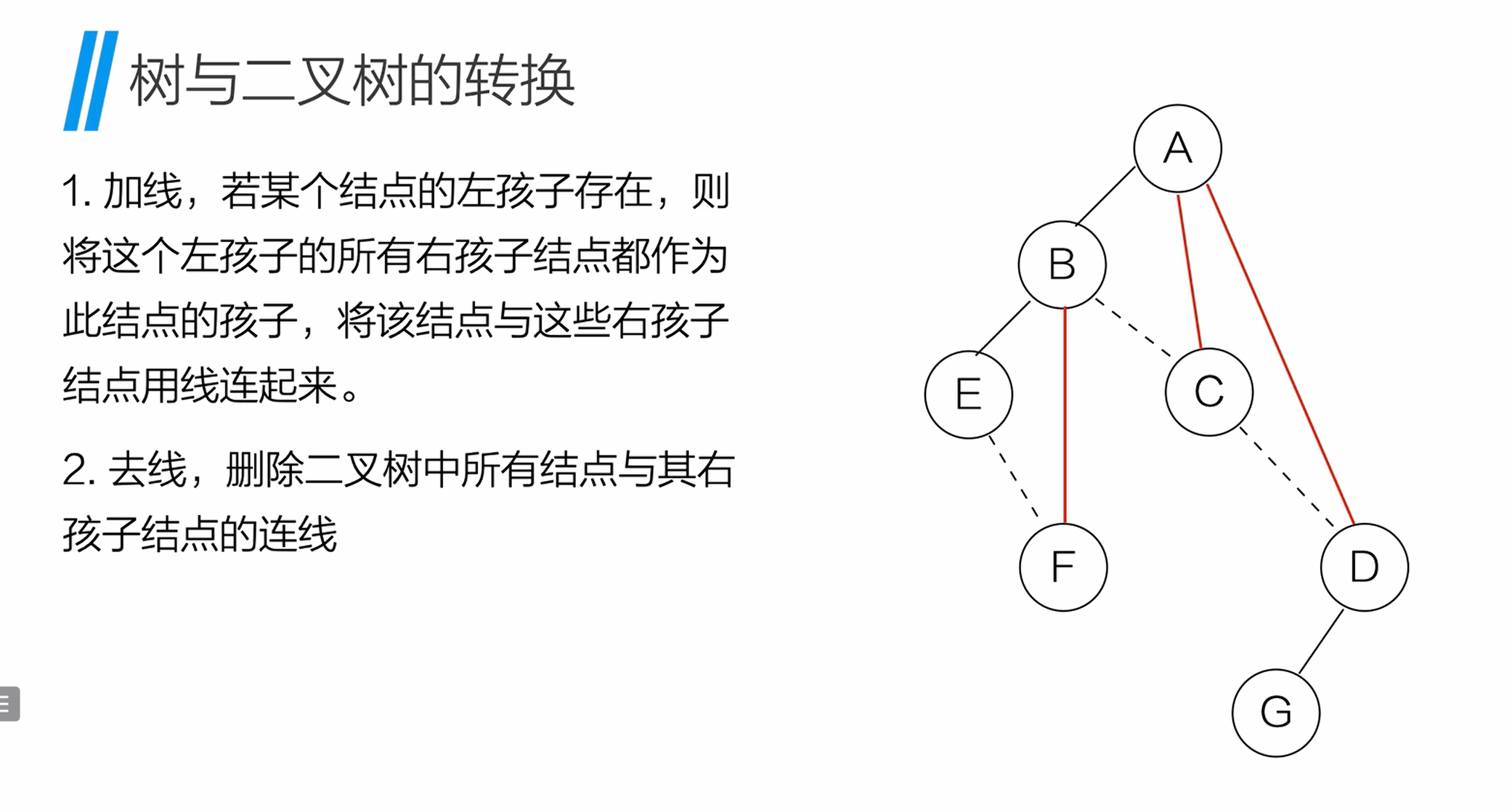
12.2 二叉树转树的步骤
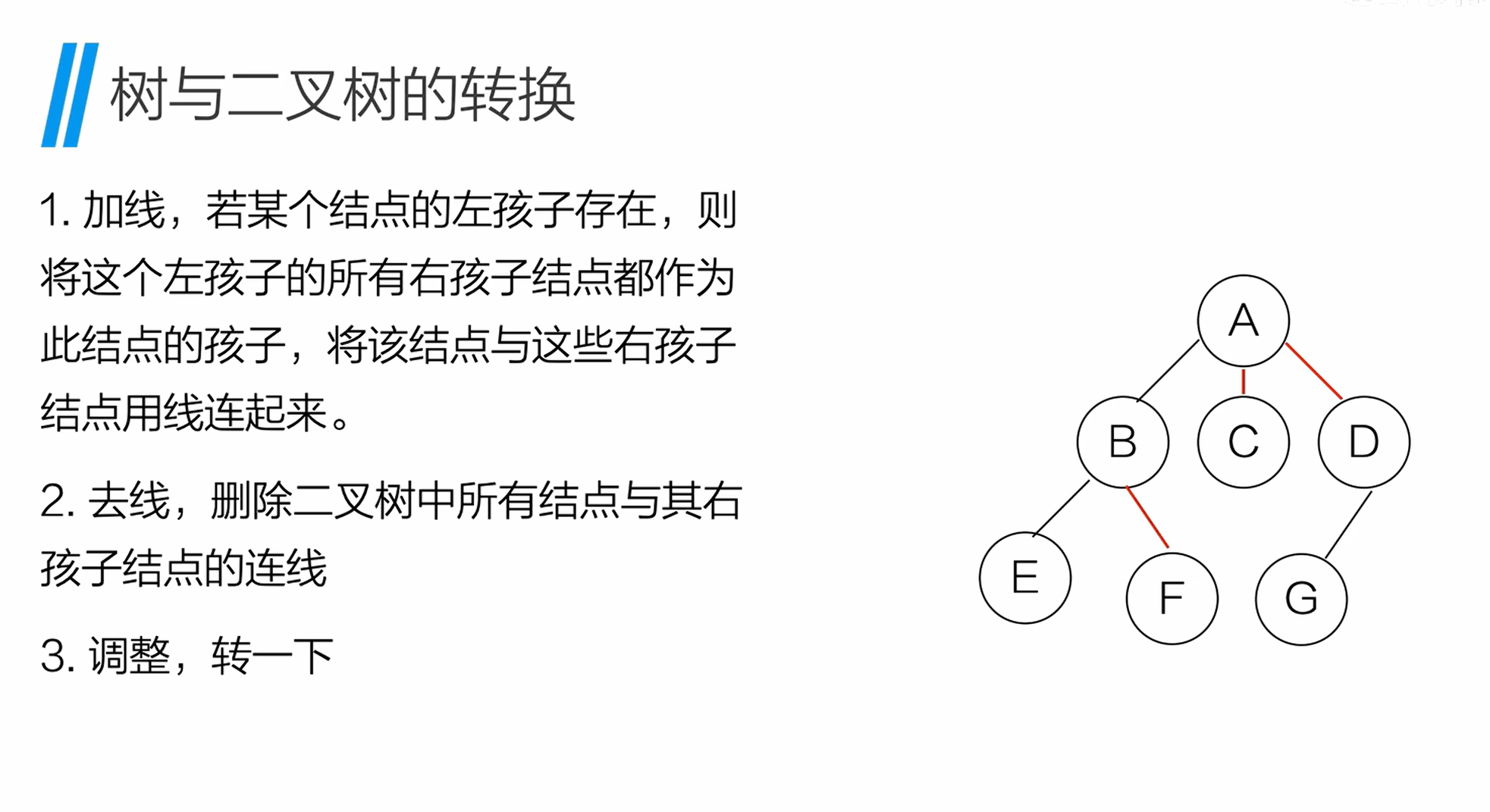
将二叉树还原为普通树:
- 加线:若节点的左孩子存在,则将左孩子的所有右孩子节点,都作为当前节点的孩子并连线;
- 去线:删除二叉树中所有节点与其右孩子的连线;
- 调整:调整节点位置,恢复普通树的层次结构。
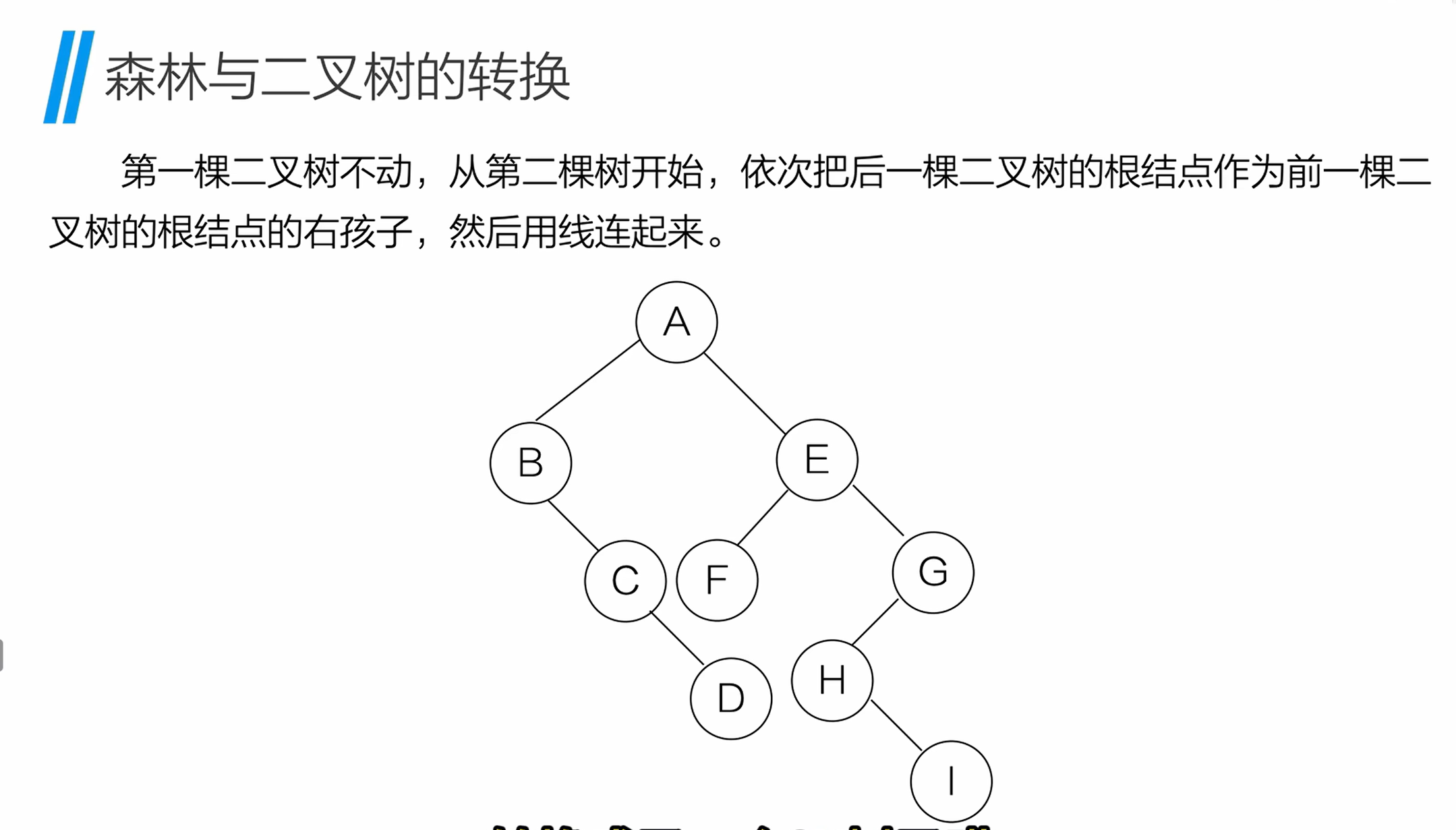
13. 森林与二叉树的转换
13.1 森林转二叉树的步骤
森林是多棵树的集合,转换为二叉树的规则:
- 将森林中的每棵树分别转换为二叉树;
- 第一棵二叉树保持不动,从第二棵二叉树开始,依次将后一棵二叉树的根节点,作为前一棵二叉树的根节点的右孩子并连线。
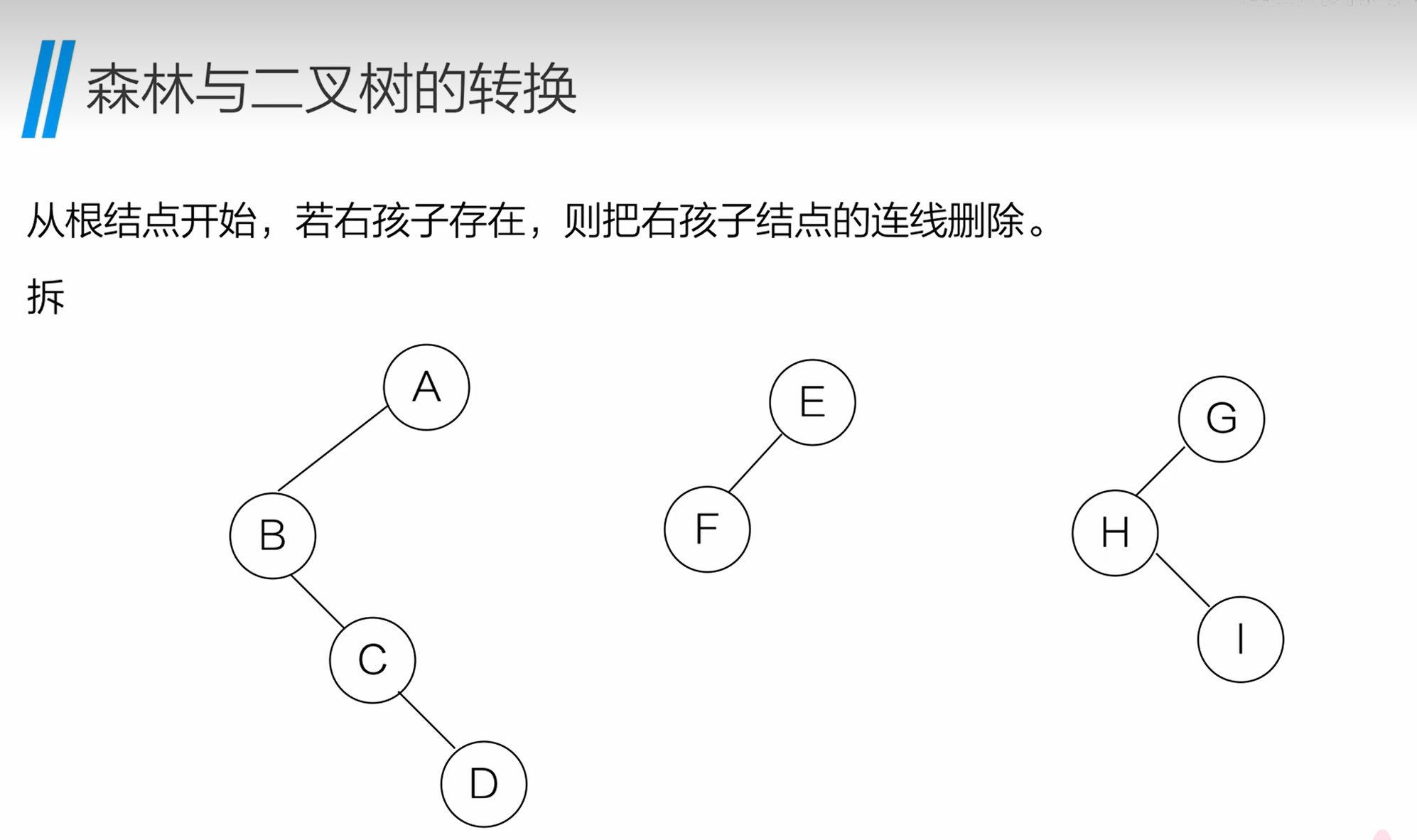
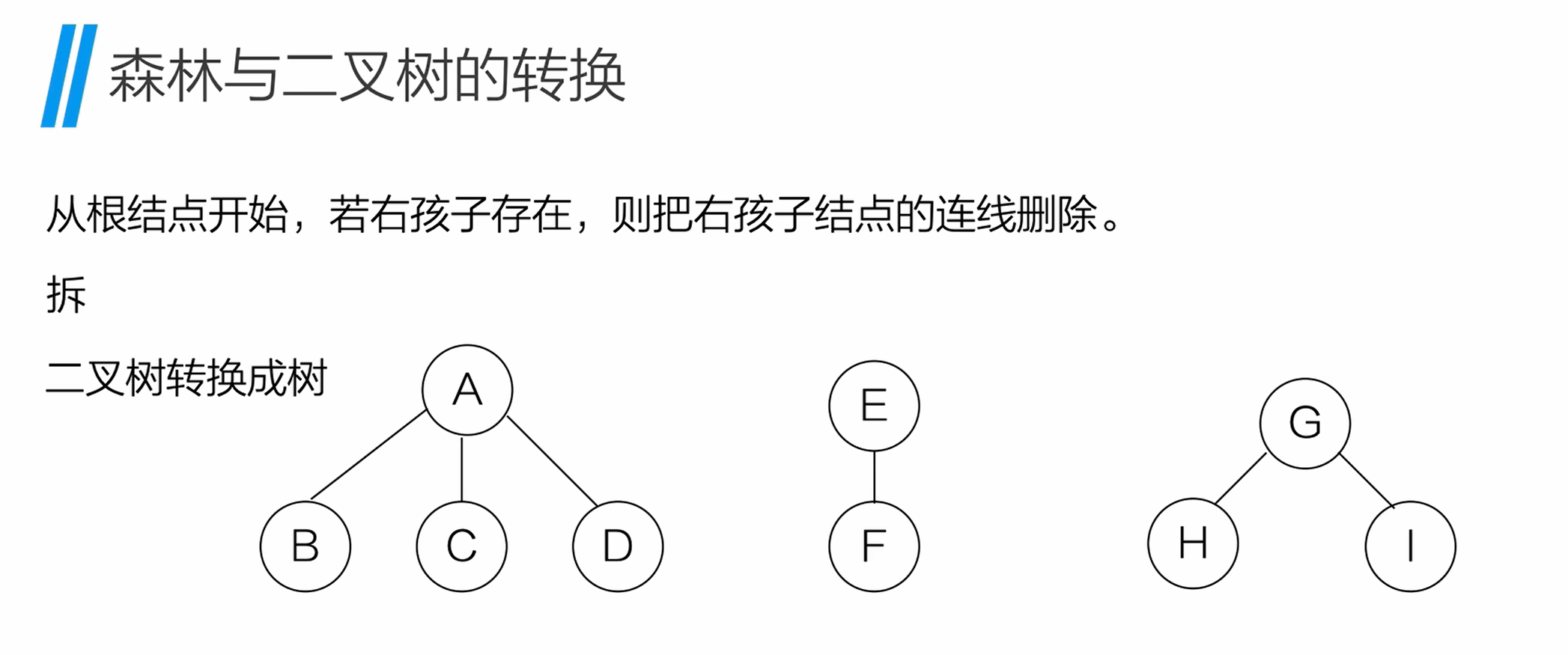
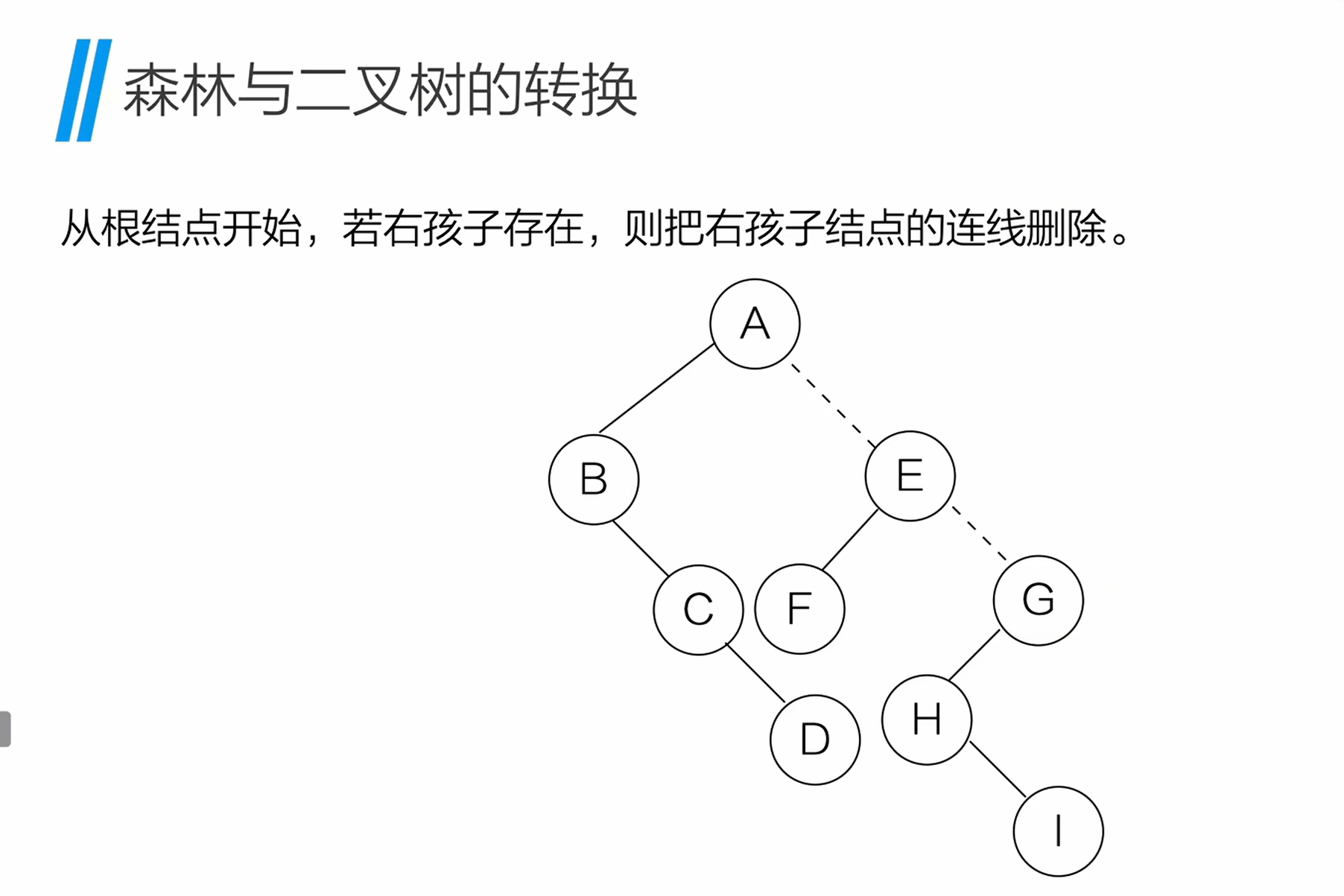
13.2 二叉树转森林的步骤
将二叉树还原为森林:
- 从根节点开始,若存在右孩子,则删除根节点与右孩子的连线,拆分出一棵新的二叉树;
- 重复步骤 1,直到所有右孩子连线都被删除;
- 将拆分出的每棵二叉树,分别还原为普通树,组成森林。
14. 正则 k 叉树的性质(真题解析)
14.1 正则 k 叉树的定义
每个非叶节点都有k个孩子的 k 叉树,称为正则 k 叉树(k≥2)。
14.2 正则 k 叉树的性质推导(2016 真题)
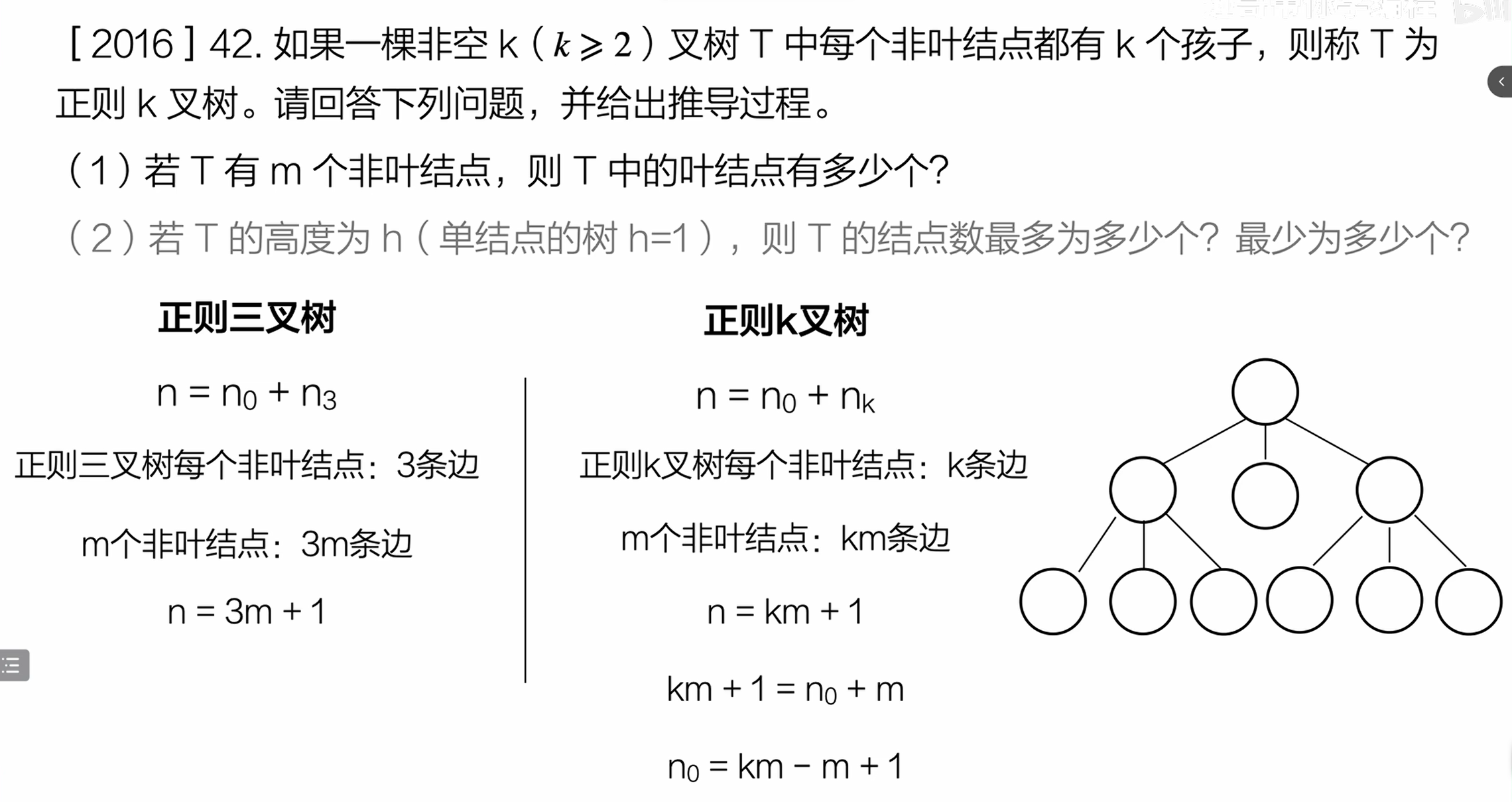
14.2.1 叶节点数与非叶节点数的关系
已知正则 k 叉树有m个非叶节点,求叶节点数n₀:
- 树的总节点数
n = n₀ + m; - 正则 k 叉树中,每个非叶节点贡献
k条边,总边数为k×m; - 树的总边数 = 总节点数 - 1(根节点无父节点),即
k×m = n - 1; - 联立得:
k×m = (n₀ + m) - 1,化简得 叶节点数n₀ = (k-1)×m + 1。
14.2.2 高度为 h 时的节点数范围
设正则 k 叉树高度为h(单节点树h=1):
- 节点数最多 :树为 "满 k 叉树",每层节点数为
k^(i-1)(i为层数),总节点数为(k^h - 1) / (k - 1); - 节点数最少 :每层仅 1 个非叶节点(其余为叶节点),总节点数为
1 + (h-1)×(k-1)(根节点 + 每层新增k-1个叶节点)。
15. 树的遍历
15.1 树的基本遍历方式
树的遍历主要有两种:
- 先根遍历:先访问根节点,再依次先根遍历各子树;
- 后根遍历:先依次后根遍历各子树,再访问根节点。
15.2 树与二叉树遍历的对应关系
树转换为二叉树后,遍历规则存在对应关系:
- 树的先根遍历 = 对应二叉树的前序遍历;
- 树的后根遍历 = 对应二叉树的中序遍历。
16. 树、森林与二叉树的遍历关系
三者的遍历规则存在如下对应关系:
| 树 | 森林 | 二叉树 |
|---|---|---|
| 先根遍历 | 前序遍历 | 前序遍历 |
| 后根遍历 | 中序遍历 | 中序遍历 |
17. 二叉树的深度计算(层序遍历实现)
17.1 算法思路
通过层序遍历(借助队列)统计二叉树的深度:每遍历完一层节点,深度加 1。
17.2 代码实现
cs
int maxDepth(TreeNode* root)
{
if (root == NULL)
{
return 0; // 空树深度为0
}
int depth = 0;
Queue *q = initQueue(); // 初始化队列
enqueue(q, root); // 根节点入队
while (!isEmpty(q))
{
int count = queueSize(q); // 当前层的节点数
while (count > 0)
{
TreeNode* curr;
dequeue(q, &curr); // 节点出队
// 左孩子入队
if (curr->lchild != NULL)
{
enqueue(q, curr->lchild);
}
// 右孩子入队
if (curr->rchild != NULL)
{
enqueue(q, curr->rchild);
}
count--;
}
depth++; // 遍历完一层,深度+1
}
return depth;
}