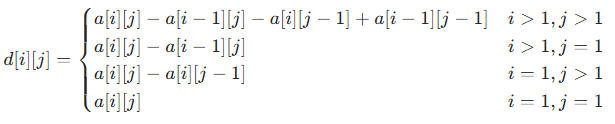前缀和与差分

前缀和与差分是一对关联性十分强的两个算法，都是对一段数组进行操作，一个是累加，一个是两两相减，话不多说上干货！！！

前缀和

前缀和分一维和二维两种，这里我主要分析二维的，一维的比较简单；

以以前写的代码展开详细描述与解释,并附上题目

cpp 复制代码

int main() 
{
    int n,m,q;
    cin>>n>>m>>q;
    vector<vector<int>> arr(n+1,vector<int>(m+1));
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cin>>arr[i][j];
        }
    }
    vector<vector<long long>> ret(n+1,vector<long long>(m+1));
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            ret[i][j]=ret[i-1][j]+ret[i][j-1]+arr[i][j]-ret[i-1][j-1];
        }
    }
    int x1,x2,y1,y2;
    while(q--)
    {
        cin>>x1>>y1>>x2>>y2;
        cout<<ret[x2][y2]-ret[x1-1][y2]-ret[x2][y1-1]+ret[x1-1][y1-1]<<endl;
    }
    return 0;
}

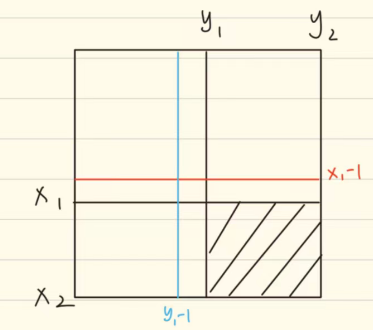
以 $i,j$ 为例，若以 $i,j$ 为例，ret $i$ $j$ 的值为以 $1,1$ 为左上角到以 $i,j$ 为右下角中所有位置的和；但是若一直使用for循环从左上角遍历到右下角进行累加，那时间复杂度太高了，不可取；所以我们应该复用之前的位置进行计算；分为两种情况，一种是求整块的面积；一种是求阴影部分的面积

求阴影部分的面积

在计算此阴影部分的面积，我们应该利用 $x1-1,y2$ $x2,y1-1$ $x1-1,y1-1$ 这三个点；因为以 $x1-1,y2$ 与 $x2,y1-1$ 位置为右下角的两个部分有重叠部分，多减的部分要加回来，即以 $x1-1,y1-1$ 为右下角部分面积，由此我们可以推出公式：

S阴影=ret $x2$ $y2$ -ret $x1-1$ $y2$ -ret $x2$ $y1-1$ +ret $x1-1$ $y1-1$

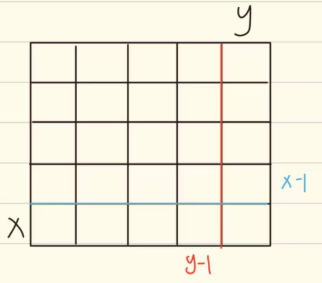
求整块的面积

在计算此阴影部分的面积，我们应该利用 $x-1,y$ $x,y-1$ $x-1,y-1$ $x,y$ 这四个点；因为以 $x-1,y$ 与 $x,y-1$ 位置为右下角的两个部分有重叠部分，多加的部分要减回来，即以 $x-1,y-1$ 为右下角部分面积，最后，还需要加上原数组中的右下角的元素 $x,y$ ,由此我们可以推出公式:

ret $x$ $y$ =ret $x-1$ $y$ +ret $x$ $y-1$ -ret $x-1$ $y-1$ +arr $x$ $y$

注：以上虽然是模板，但是因为变量较多，不建议背诵，需要大家私底下自己画图推导，方为上策！！！

差分

差分分为一维与二维，与前缀和不同，差分这个概念我们比较陌生，所以，应该我会把一维与二维都详细推导一遍；

以以前写的代码展开详细描述与解释,并附上题目

一维差分

cpp 复制代码

typedef long long ll;
const int N = 5e5 + 10;
ll f[N];//差分数组

int main()
{
    int n, q;
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        f[i] += x;
        f[i + 1] -= x;
    }
    while (q--)
    {
        ll l, r, k;
        cin >> l >> r >> k;
        f[l] += k;
        f[r + 1] -= k;
    }
    for (int i = 1; i <= n; i++)
    {
        f[i] = f[i - 1] + f[i];
        cout << f[i] << " ";
    }
    return 0;
}

一维差分介绍：一维差分 是一种用于高效处理数组区间更新与查询 的技巧，其核心思想是通过构造一个差分数组，将对原数组的区间批量修改 操作转化为差分数组的单点修改 ，从而将时间复杂度从 O(n) 优化到 O(1)，常与前缀和配合使用

具体过程如下

差分数组初始化：d $1$ =a $1$ d $i$ =a $i$ −a $i-1$ (2≤i≤n)

二维差分

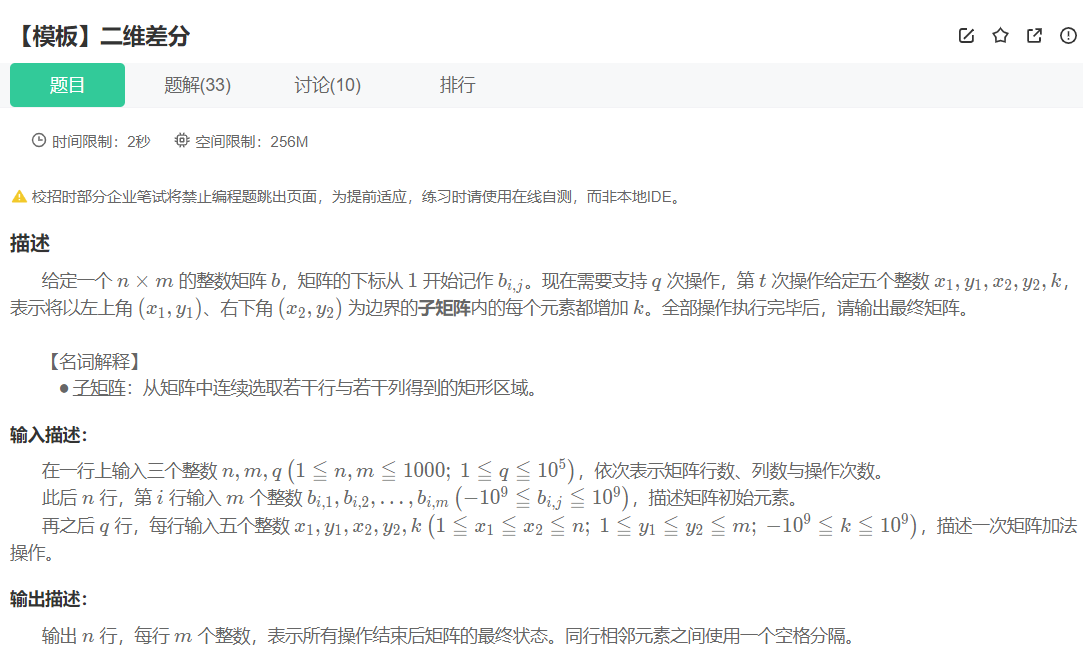
cpp 复制代码

typedef long long LL;
const int N=1010;
int n,m,q;
LL f[N][N];

void insert(int x1,int y1,int x2,int y2,LL k)
{
    f[x1][y1]+=k;f[x1][y2+1]-=k;f[x2+1][y1]-=k;f[x2+1][y2+1]+=k;
}

int main()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            int x;cin>>x;
            insert(i,j,i,j,x);
        }
    }
    while(q--)
    {
        int a,b,c,d,k;cin>>a>>b>>c>>d>>k;
        insert(a,b,c,d,k);
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+f[i][j];
            cout<<f[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}

二维差分介绍：二维差分是一维差分的扩展，用于高效处理二维数组的矩形区域批量更新，核心目标是将矩形区域的加 / 减操作从 O(nm) 的时间复杂度优化为 O(1)，常与二维前缀和配合使用，广泛应用于矩阵区间修改、图像处理等场景

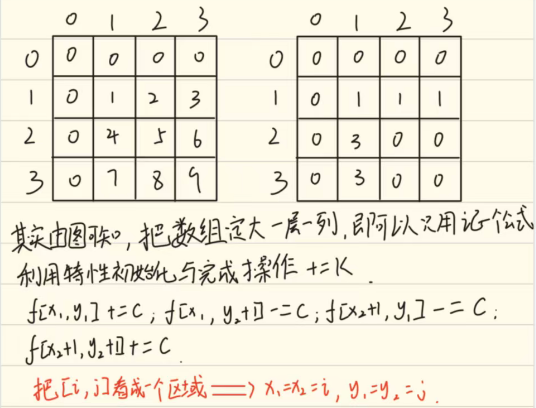
具体过程如下

初始化差分数组

操作二维数组

优化

综合练习------借教室

这是一道综合二分和差分和前缀和的综合题，有助于提升大家可以写写看

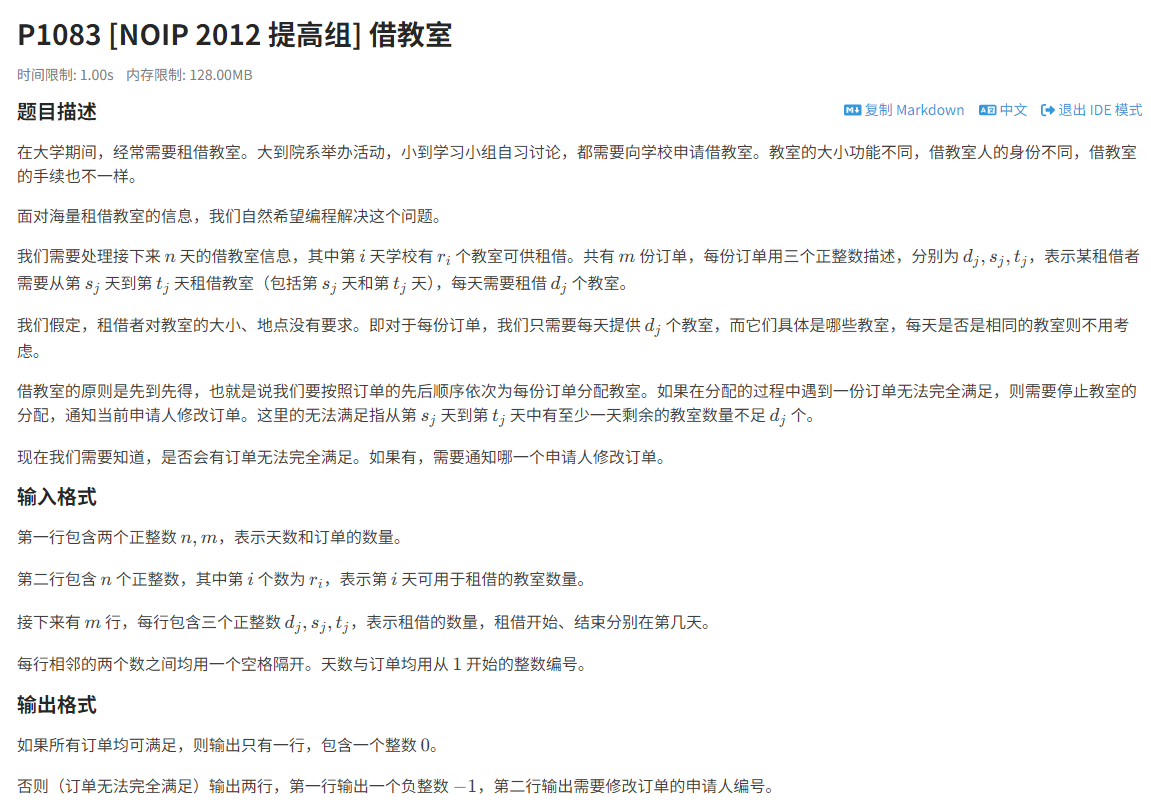
题目连接：https://www.luogu.com.cn/problem/P1083

cpp 复制代码

const int N=1e6+10;
int f[N],r[N];
int d[N],s[N],t[N];
int n,m;

//1到x天的订单情况
bool check(int x)
{
    //初始化整个差分数组
    for(int i=1;i<=n;i++)
        f[i]=r[i]-r[i-1];
    //在对应区间减去教室数
    //对应的
    for(int i=1;i<=x;i++)
    {
        f[s[i]]-=d[i];
        f[t[i]+1]+=d[i];
    }
    //还原整个数组数组
    for(int i=1;i<=n;i++)
    {
        f[i]=f[i-1]+f[i];
        if(f[i]<0) return false;
    }
    return true;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>r[i];
    for(int i=1;i<=m;i++) cin>>d[i]>>s[i]>>t[i];
    int l=1,r=m;
    while(l<r)
    {
        int mid=(l+r)/2;
        if(check(mid)) l=mid+1;
        else r=mid;
    }
    //判断结果这个点
    if(check(l)) cout<<0<<endl;
    else cout<<-1<<endl<<l<<endl;;
    return 0;
}