【计算机视觉】06_描述子

1. 为什么要进行特征描述？

我们在上一讲找到了图像中的"关键点"（Keypoints），但仅有位置是不够的。 为了将一张图中的特征点与另一张图中的特征点对应起来，我们需要围绕每个特征点提取向量 ，这个向量就是特征描述子。

• 目标： 对每一个特征点有一个描述子，并在两张图像之间寻找相似的描述子。
• 好的描述子的标准：不变性 (Invariance)： 即使图像发生了变换（旋转、缩放、亮度变化），描述子也不应当改变。
• 可判别性 (Discriminability)： 对于每一个特征点，描述子应当具有唯一性，能够区分不同的点。

描述子的解释

假设你有两张照片：

• 图 A： 埃菲尔铁塔的正面照。

• 图 B： 埃菲尔铁塔的侧面照（旋转了，甚至光线变暗了）。

你用 Harris 在两张图里都找到了"塔尖"这个角点。

• 图 A 的塔尖坐标是 (100, 100)。

• 图 B 的塔尖坐标是 (500, 600)。

计算机怎么知道 图 A 的 (100, 100) 和 图 B 的 (500, 600) 是同一个物理点呢？ 如果你只比较坐标，它们完全不同。 如果你只比较那个点周围的像素值（RGB），因为光线变了、旋转了，像素值也完全对不上。

这就是描述子的作用： 我们要把这个点周围的图像信息，转换成一串数字（向量） 。这串数字必须具有**"特异性"和"鲁棒性"**------不管你怎么旋转、缩放、变暗，这串数字最好保持不变

2. 几种常见的描述子策略

A. 简单的图像块 (Simple Square Window)

最简单的方法是直接提取特征点周围的像素块（例如 40×4040 \times 4040×40 的窗口），但这通常不足以应对复杂的几何变换。

B. MOPS (Multiscale Oriented PatcheS)

这是一种更先进的策略，旨在解决旋转和光照问题：

1. 旋转不变性： 找到图像块的主导方向（例如梯度的方向），并将图像块旋转到水平方向。
2. 光照不变性： 对窗口内的像素进行亮度归一化（减去均值，除以标准差）。
3. 尺度处理： 在多尺度金字塔上进行检测和采样（例如缩放到 1/5 尺寸）。

C. SIFT (Scale Invariant Feature Transform) ------ 行业标杆

SIFT 是计算机视觉中最著名的描述子之一，由 David Lowe 提出。它具有非常强的鲁棒性。

• 核心思想：使用梯度直方图。
• SIFT 不直接使用像素亮度值，而是计算像素的梯度值 和梯度方向。相比亮度值，梯度对光照变化具有更好的鲁棒性。

1. 构建过程：计算梯度： 计算特征点周围区域的梯度大小和方向。
2. 高斯加权： 利用高斯核对梯度进行加权，离中心越近的像素权重越大。
3. 主方向归一化： 建立梯度方向直方图，选择梯度值最大的那个角度 作为主方向。将周围图像相对于主方向旋转，从而实现旋转不变性。
4. 生成描述子： 将区域划分为子区域（如 4×44 \times 44×4），在每个子区域统计梯度方向直方图（8个方向），最后连接成一个长向量（通常是 4×4×8=1284 \times 4 \times 8 = 1284×4×8=128 维向量）。

• 特性： SIFT 能处理视角变化、显著的光照变化，且处理速度相对较快。

3. 特征匹配 (Feature Matching)

有了描述子向量 f1f_1f1 和 f2f_2f2 后，如何判断它们是否匹配？

A. 距离度量

• L2 距离： 计算两个向量之间的欧氏距离 ∣∣f1−f2∣∣||f_1 - f_2||∣∣f1−f2∣∣。
• 阈值问题： 距离多少算匹配？这很难定。

B. 比值测试 (Ratio Test) ------ 关键技巧

为了剔除歧义匹配 （例如重复的纹理，一个点在另一张图中有多个看起来都很像的匹配点），Lowe 提出了比值距离策略：

Ratio=∣∣f1−f2∣∣∣∣f1−f2′∣∣ Ratio = \frac{||f_1 - f_2||}{||f_1 - f_2'||} Ratio=∣∣f1−f2′∣∣∣∣f1−f2∣∣

• 其中 f2f_2f2 是最佳匹配点（距离最近）。
• f2′f_2'f2′ 是次优匹配点（距离第二近）。
• 原理： 如果 f2f_2f2 是正确的匹配，那么它应该比 f2′f_2'f2′ 近得多（比值小）。如果比值接近 1，说明存在歧义，应当丢弃该匹配。

4. 结果评价

如何衡量匹配算法的好坏？我们通常使用 ROC 曲线：

• TP (True Positives)： 检测到的正确匹配。
• FP (False Positives)： 检测到的错误匹配。
• ROC 曲线： 绘制 TP率 vs. FP率 的曲线。曲线下的面积 (AUC ) 越大，算法性能越好（1 为最佳）。
  

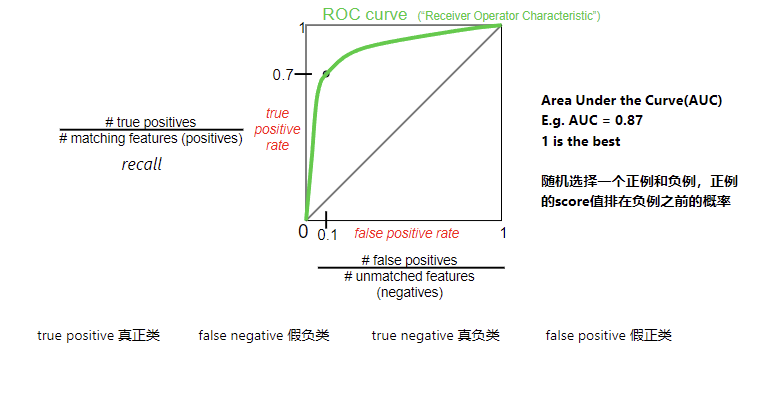
ROC 曲线的解释

1. 坐标轴：一场"激进"与"保守"的博弈

这张图的横纵坐标，其实就是在展示你在**"不想漏掉坏人"和"不想冤枉好人"**之间是如何做权衡的。

• 纵轴 (Y轴): True Positive Rate (真阳性率) / Recall (召回率)

  • 公式： 抓对的坏人所有的坏人\frac{\text{抓对的坏人}}{\text{所有的坏人}}所有的坏人抓对的坏人 (如图中所示: # true positives / # matching features)。

  • 含义： 你成功找出了多少正确的匹配？

  • 目标： 越高越好（也就是图里写的 recall）。

• 横轴 (X轴): False Positive Rate (假阳性率)

  • 公式： 误抓的好人所有的好人\frac{\text{误抓的好人}}{\text{所有的好人}}所有的好人误抓的好人 (如图中所示: # false positives / # unmatched features)。

  • 含义： 你在乱抓人的时候，冤枉了多少不该匹配的特征？

  • 目标： 越低越好。

2. 绿色的曲线：你的能力边界

这条绿线是由不同的阈值 (Threshold) 连出来的。

• 想象一下：

  • 如果你把标准定得很低（宁可错杀一千，不可放过一个），你的 Y 轴很高（坏人都抓住了），但 X 轴也很高（好人也被冤枉了）。这是曲线的右上角。

  • 如果你把标准定得很高（绝不冤枉好人），你的 X 轴很低（没误报），但 Y 轴也很低（坏人都跑了）。这是曲线的左下角。

• 完美的算法： 应该在左上角 (0, 1)。这意味着：抓住了所有坏人 (Y=1)，且没有冤枉任何好人 (X=0)。

总结： 本课件讲解了如何通过 SIFT 等算法将图像中的关键点转化为具有不变性的向量描述子 ，并通过比值测试策略在不同图像间建立可靠的连接。