OpenMP是一个用于编写并行程序的应用编程接口。
1.构成OpenMP通用核心的编译指令、运行时库函数和子句以及相关的多线程计算基本概念:
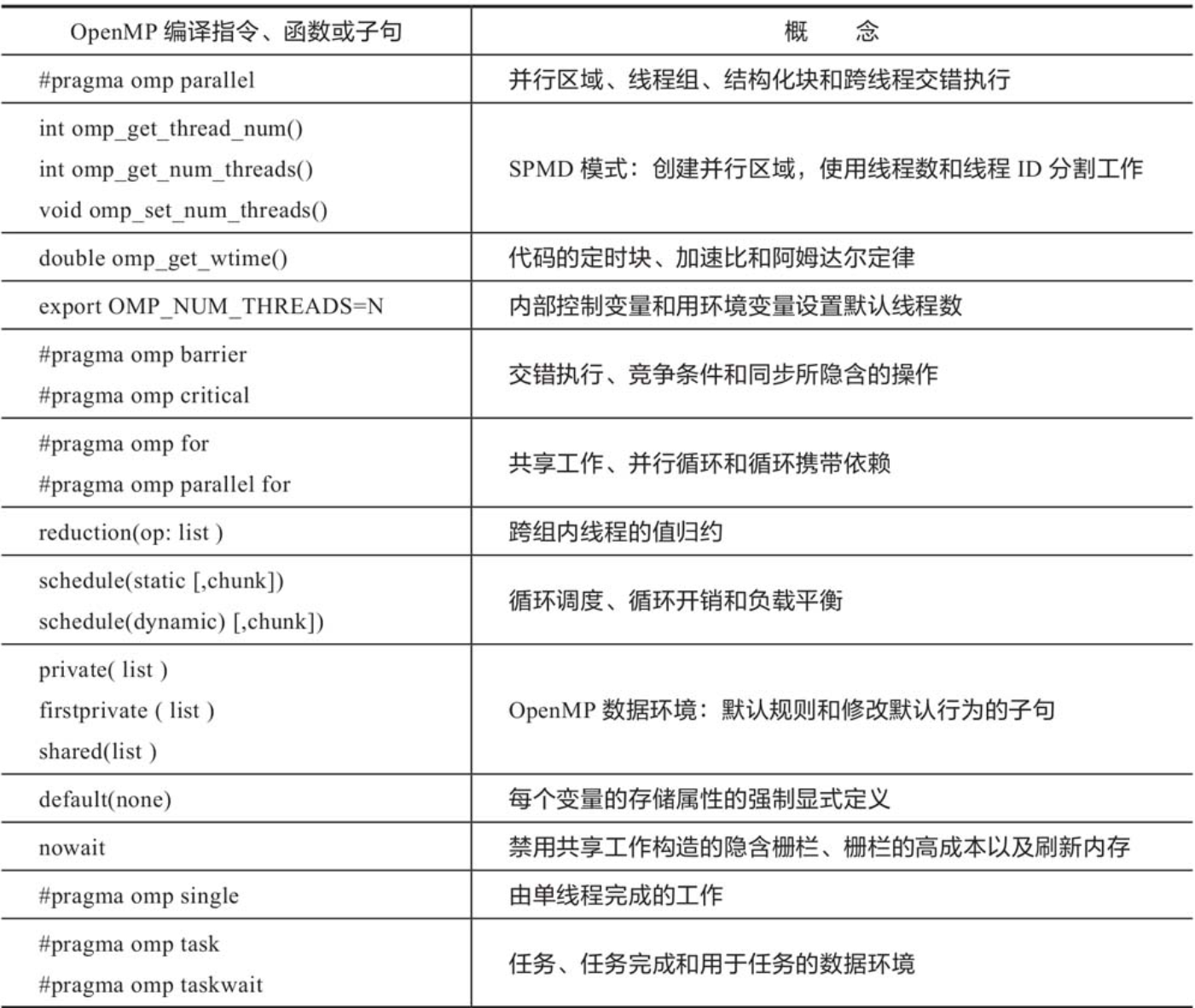
2.用于OpenMP通用核心的解决方案栈:
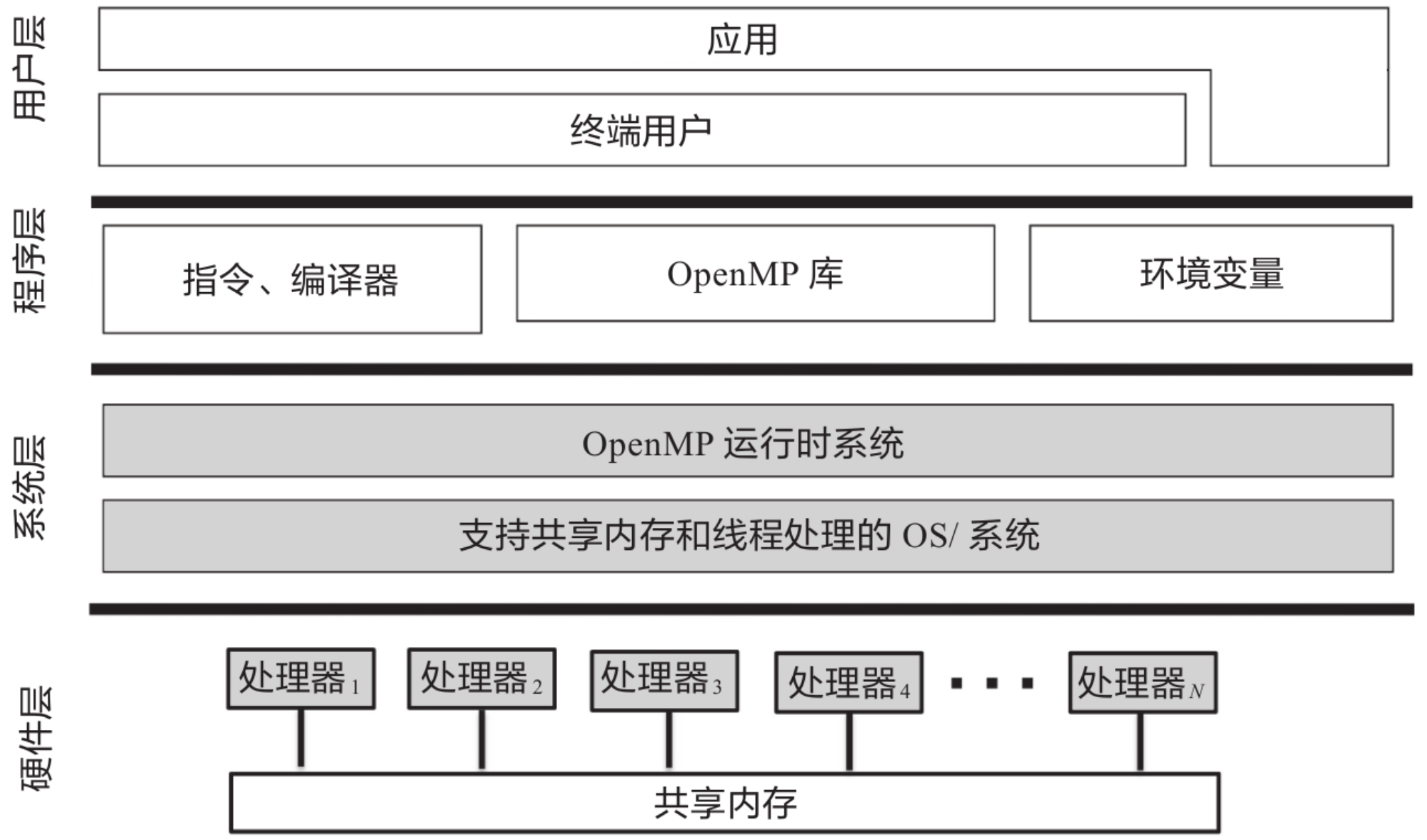
3.openmp构造线程的基本形式

OpenMP 是一种基于共享内存(Shared Memory)的并行编程标准。 对于 C++ 开发者来说,它最直观的特点是非侵入式的------我们不需要像 std::thread 那样重写很多代码,只需要在循环或代码块前加上 #pragma 编译指令,编译器就会自动帮我们将任务分配到多个 CPU 核心上执行。
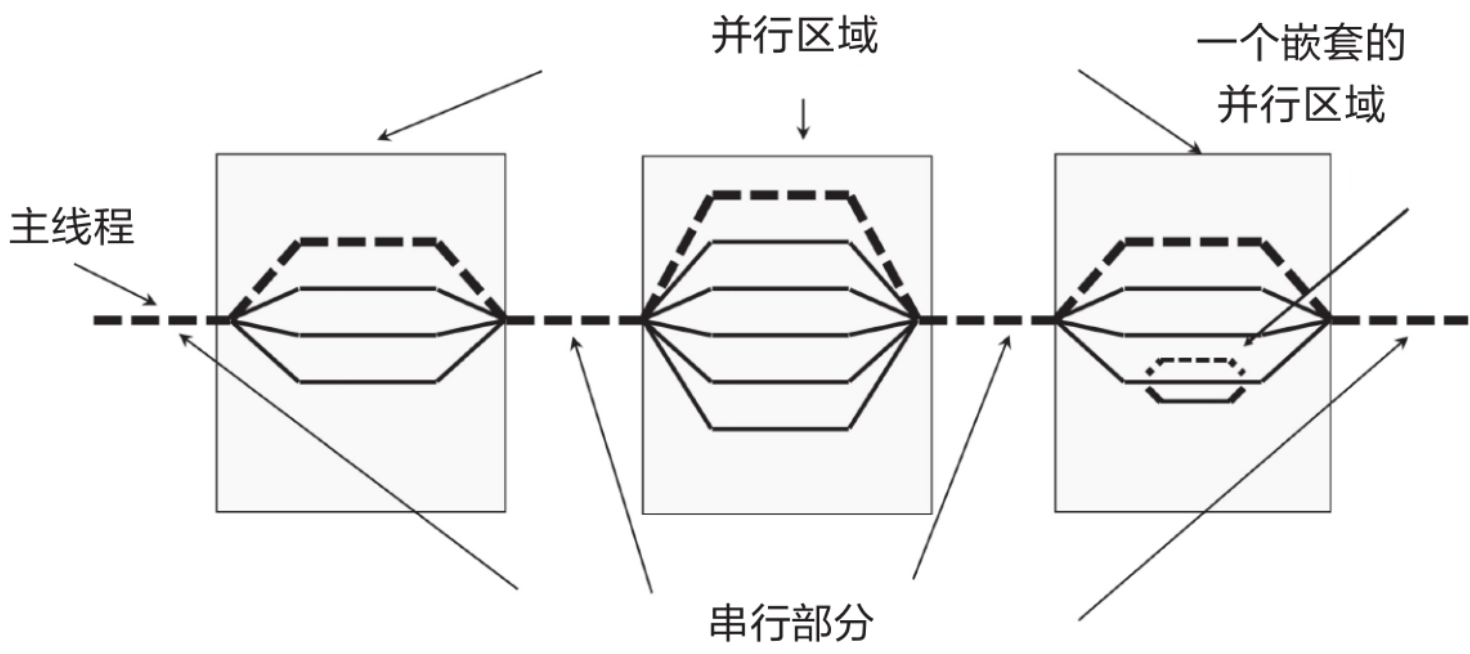
程序开始时是单线程(Master Thread)执行;遇到并行指令(如 #pragma omp parallel)时,主线程会 Fork 出一组子线程(Team of Threads)来并行处理任务;任务结束后,这些线程会同步并 Join(汇合),释放资源,恢复到单线程继续执行。 这非常适合处理那种'数据相互独立、计算量大'的循环任务(Data Parallelism)。

返回线程序号:

返回当前线程组中的线程总数:
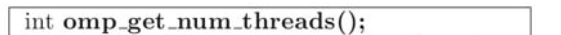
示例:
cpp
#include <stdio.h>
#include <omp.h>
int main(){
omp_set_num_threads(4);
int size_of_team;
#pragma omp parallel
{
int ID = omp_get_thread_num();
int NThrds = omp_get_num_threads();
if(ID == 0) size_of_team = NThrds;
}
printf("We just did the join on a team of size %d", size_of_team);
}命令为:
bash
gcc -fopenmp demo1.c
bash
.\a.exe输出:
bash
We just did the join on a team of size 4并行化练习:
将这个程序并行化:
cpp
#include <stdio.h>
#include <omp.h>
static long num_steps = 100000000;
double step;
int main ()
{
int i;
double x, pi, sum = 0.0;
double start_time, run_time;
step = 1.0 / (double) num_steps;
start_time = omp_get_wtime();
for (i = 0; i < num_steps; i++){
x = (i + 0.5) * step;
sum += 4.0 / (1.0 + x * x);
}
pi = step * sum;
run_time = omp_get_wtime() - start_time;
printf(" pi = %lf , %ld steps, %lf secs\n ", pi, num_steps, run_time);
}并行化前,我电脑上运行时间: 0.185000 secs
方法1:对循环迭代按周期划分
cpp
#include <stdio.h>
#include <omp.h>
#define NTHREADS 4
static long num_steps = 100000000;
double step;
int main ()
{
int i;
int j, actual_nthreads;
double x, pi;
double start_time, run_time;
double sum[NTHREADS] = {0.0};
step = 1.0 / (double) num_steps;
omp_set_num_threads(NTHREADS);
start_time = omp_get_wtime();
#pragma omp parallel
{
int i;
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
double local_sum = 0.0;
if(id == 0) actual_nthreads = numthreads;
for (i = id; i < num_steps; i += numthreads){
x = (i + 0.5) * step;
sum[id] += 4.0 / (1.0 + x * x); //
}
}
pi = 0;
for(i = 0; i < actual_nthreads; i++)
pi += sum[i];
pi = step * pi;
run_time = omp_get_wtime() - start_time;
//
printf(" pi = %lf , %ld steps, %lf secs\n ", pi, num_steps, run_time);
}但是实际测试发现,运行时间为: 0.453000 secs
时间变长了,原因是定义的数组 sum[NTHREADS] 太小了,导致不同线程在争抢同一块 CPU 缓存行,也就是伪共享问题。
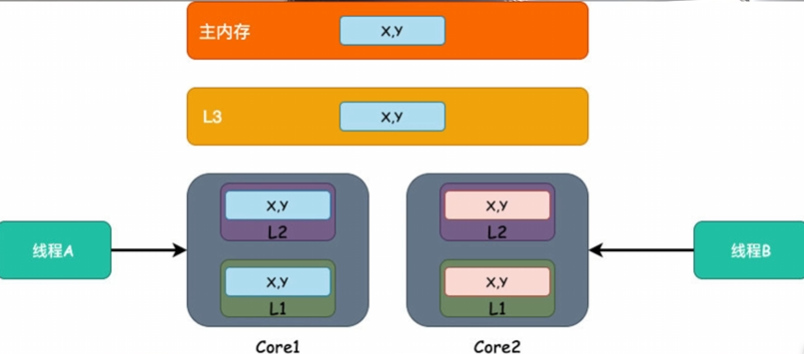
现代 CPU 的缓存行通常是 64 字节 。整个数组大小 = 4 × 8 = 32 字节。sum[0], sum[1], sum[2], sum[3] 极大概率全部挤在同一个 64 字节的缓存行里。
- 核心 0 想更新 sum[0]。为了写入,它必须独占这行缓存,这会导致核心 1、2、3 缓存里的这行数据失效。
- 核心 1 想更新 sum[1]。它发现缓存失效了,必须重新从内存(或 L3)拉取数据,并告诉其他核心"你们的缓存失效了"。
- 核心 2 想更新 sum[2]......
- 核心 3 想更新 sum[3]......
这就好比 4 个人在一张小纸条上同时写字,每个人写之前都要把纸条从别人手里抢过来。在这个 1 亿次的循环中,CPU 核心把大量时间花在了争抢缓存行的所有权(Cache Coherency 协议,如 MESI)上,而不是在做计算。这比单线程没有任何争抢要慢得多。
这时候要避免上面的问题,有两种方法:
(1)字节填充
给数组增加第二个维度,那sum[1][0]就可以足够占满一个缓存行。
但是这样也会增加空间消耗,不过在这里还好,sum数组很小。
时间和空间的消耗要学会自己取舍。
cpp
#include <stdio.h>
#include <omp.h>
#define NTHREADS 4
#define CBLK 8
static long num_steps = 100000000;
double step;
int main()
{
int i, j, actual_nthreads;
double pi, start_time, run_time;
double sum[NTHREADS][CBLK] = {0.0};
step = 1.0 / (double) num_steps;
omp_set_num_threads(NTHREADS);
start_time = omp_get_wtime();
#pragma omp parallel
{
int i;
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
if (id == 0)
actual_nthreads = numthreads;
for (i = id; i < num_steps; i += numthreads) {
x = (i + 0.5) * step;
sum[id][0] += 4.0 / (1.0 + x * x);
}
} // end of parallel region
pi = 0.0;
for (i = 0; i < actual_nthreads; i++)
pi += sum[i][0];
pi = step * pi;
run_time = omp_get_wtime() - start_time;
printf("\n pi is %f in %f seconds %d thrds \n",
pi, run_time, actual_nthreads);
}(2)减少对数组的频繁访问
引入一个局部变量,把对数组的操作移动到for循环之外:
cpp
#pragma omp parallel
{
int i;
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
double local_sum = 0.0;
if(id == 0) actual_nthreads = numthreads;
for (i = id; i < num_steps; i += numthreads){
x = (i + 0.5) * step;
local_sum += 4.0 / (1.0 + x * x); // 原:sum[id] +=
}
sum[id] = local_sum; // 新增这一行
}完整代码:
cpp
#include <stdio.h>
#include <omp.h>
#define NTHREADS 4
static long num_steps = 100000000;
double step;
int main ()
{
int i;
int j, actual_nthreads;
double x, pi;
double start_time, run_time;
double sum[NTHREADS] = {0.0};
step = 1.0 / (double) num_steps;
omp_set_num_threads(NTHREADS);
start_time = omp_get_wtime();
#pragma omp parallel
{
int i;
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
double local_sum = 0.0;
if(id == 0) actual_nthreads = numthreads;
for (i = id; i < num_steps; i += numthreads){
x = (i + 0.5) * step;
local_sum += 4.0 / (1.0 + x * x); // 原:sum[id] +=
}
sum[id] = local_sum; // 新增这一行
}
pi = 0;
for(i = 0; i < actual_nthreads; i++)
pi += sum[i];
pi = step * pi;
run_time = omp_get_wtime() - start_time;
//
printf(" pi = %lf , %ld steps, %lf secs\n ", pi, num_steps, run_time);
}运行时间为:0.048000 secs
方法2:基于循环的块状分解,在线程间分配循环工作
在分块 方式中,我们需要让每个线程处理连续的一段任务。其实就是按照顺序分块,一个块给一个线程执行,例如,线程 0 处理前半部分,线程 1 处理后半部分。
cpp
/**
* @file demo_pi_mp_2.c
* @author your name (you@domain.com)
* @brief 基于循环的块状分解,在线程间分配循环工作
* 其实就是按照顺序分块,一个块给一个线程执行
*
* @version 0.1
* @date 2025-12-22
*
* @copyright Copyright (c) 2025
*
*/
#include <stdio.h>
#include <omp.h>
#define NTHREADS 4
static long num_steps = 100000000;
double step;
int main ()
{
int i;
int j, actual_nthreads;
double x, pi;
double start_time, run_time;
double sum[NTHREADS] = {0.0};
step = 1.0 / (double) num_steps;
omp_set_num_threads(NTHREADS);
start_time = omp_get_wtime();
#pragma omp parallel
{
int i;
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
int local_sum = 0;
if(id == 0) actual_nthreads = numthreads;
int block_size = num_steps / numthreads;
int istart = id * block_size;
int iend = (id + 1) * block_size;
for (i = istart; i < iend; i++){
x = (i + 0.5) * step;
local_sum += 4.0 / (1.0 + x * x); // 原:sum[id] +=
}
sum[id] = local_sum; // 新增这一行
}
pi = 0;
for(i = 0; i < actual_nthreads; i++)
pi += sum[i];
pi = step * pi;
run_time = omp_get_wtime() - start_time;
//
printf(" pi = %lf , %ld steps, %lf secs\n ", pi, num_steps, run_time);
}运行时间:0.110000 secs