【算法基础篇】（五十六）容斥原理指南：从集合计数到算法实战，解决组合数学的 “重叠难题”！

前言

你有没有遇到过这样的问题：统计班里喜欢足球或篮球的同学人数，直接把两者相加却发现重复算了既喜欢足球又喜欢篮球的人；计算 1 到 100 中能被 2 或 3 整除的数，简单相加后结果明显偏多；甚至在复杂的算法题中，因为没考虑元素的重叠关系，导致答案错误。

这些问题的核心痛点，都指向了组合数学中的 "重叠计数" 难题。而解决这类问题的万能钥匙，就是容斥原理（Inclusion-Exclusion Principle）。

容斥原理是组合数学中最基础也最强大的计数工具之一，它的核心思想是 "先不考虑重叠，再排除重复，补回遗漏"，完美解决了多集合交集的计数问题。无论是算法面试中的经典题型（如倍数统计、集合筛选），还是实际开发中的排列组合场景，容斥原理都能发挥巨大作用。

本文将从生活场景切入，带你层层拆解容斥原理的本质，推导核心公式，再通过 6 道梯度例题，手把手教你用 C++ 实现高效解法。无论你是算法新手，还是想巩固组合数学基础的开发者，读完这篇文章，都能彻底掌握容斥原理的核心逻辑，轻松应对各类 "重叠计数" 问题！下面就让我们正式开始吧！

一、容斥原理的定义：什么是 "先加后减，补漏去重"？

1.1 核心思想

容斥原理的本质是：在计数时，先不考虑集合间的重叠关系，将所有满足条件的元素个数相加；然后减去重复计算的部分（两个集合的交集）；再补回被多减的部分（三个集合的交集）；以此类推，直到计算出所有集合的并集大小，最终得到无重复、无遗漏的计数结果。

简单来说，就是 "加加减减，补漏去重"。

1.2 从生活案例理解容斥

举个最常见的例子：

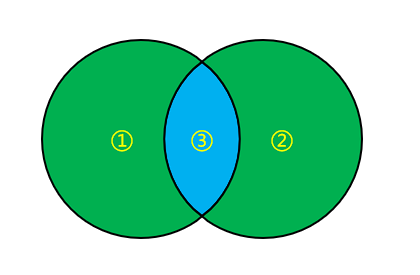
班里有 12 人喜欢足球（集合 A），14 人喜欢篮球（集合 B），其中 3 人既喜欢足球又喜欢篮球（A∩B），求喜欢足球或篮球的总人数。

直接相加：12+14=26，但这 3 人被重复计算了一次，所以需要减去重复部分：26-3=23，最终结果为 23 人。

再复杂一点：

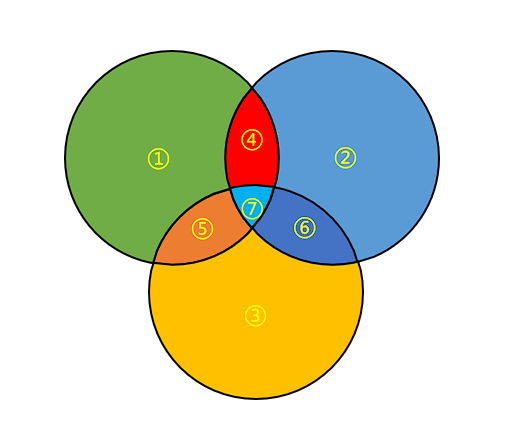
班里有 12 人喜欢足球（A），14 人喜欢篮球（B），16 人喜欢乒乓球（C），2 人既喜欢 A 又喜欢 B，3 人既喜欢 B 又喜欢 C，4 人既喜欢 A 又喜欢 C，1 人三种都喜欢（A∩B∩C），求喜欢至少一种运动的人数。

计算过程：12+14+16 - (2+3+4) + 1 = 34，最终结果为 34 人。

这两个例子，分别对应了容斥原理在两个集合和三个集合中的应用，其核心逻辑可以推广到 n 个集合的场景。

1.3 数学公式表达

（1）两个集合的容斥原理

对于任意两个集合 A 和 B，它们的并集大小为：∣A∪B∣=∣A∣+∣B∣−∣A∩B∣

解释：A 和 B 的总元素数 = A 的元素数 + B 的元素数 - 两者重叠的元素数。

（2）三个集合的容斥原理

对于任意三个集合 A、B、C，它们的并集大小为：∣A∪B∪C∣=∣A∣+∣B∣+∣C∣−∣A∩B∣−∣A∩C∣−∣B∩C∣+∣A∩B∩C∣

解释：先加三个集合的元素数，再减去每两个集合的重叠部分，最后补回三个集合都重叠的部分（因为前面多减了一次）。

（3）n 个集合的容斥原理

Q对于 n 个集合A1,A2,...,An，它们的并集大小为：

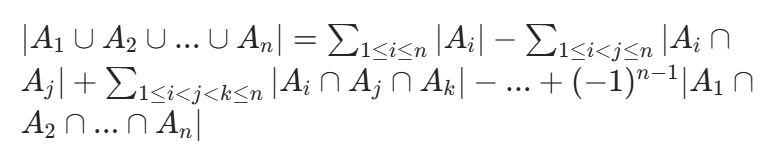
规律：奇数个集合的交集相加，偶数个集合的交集相减，直到最后一个 n 个集合的交集（符号为）。

二、容斥原理的核心应用场景：如何快速识别 "容斥题"？

容斥原理的应用场景非常广泛，但核心特征都围绕 "至少满足一个条件 " 或 "排除不满足所有条件"，常见场景包括：

**倍数统计：**统计 1 到 n 中能被 a 或 b 或 c 整除的数的个数；

**集合筛选：**统计至少能被集合中一个质数整除的数的个数；

**多重限制：**解决 "不超过某个限制""至少满足一个约束" 的组合计数问题；

**正难则反：**当直接计算目标条件困难时，先计算反面（不满足任何条件），再用总数减去反面结果。

只要题目中出现 "或""至少一个""不超过" 等关键词，且存在条件重叠的可能，就可以考虑用容斥原理求解。

三、容斥原理的 C++ 实现：6 道例题从入门到高阶

3.1 例题 1：大水题（牛客网）------ 基础容斥，四集合倍数统计

题目链接：https://ac.nowcoder.com/acm/problem/15079

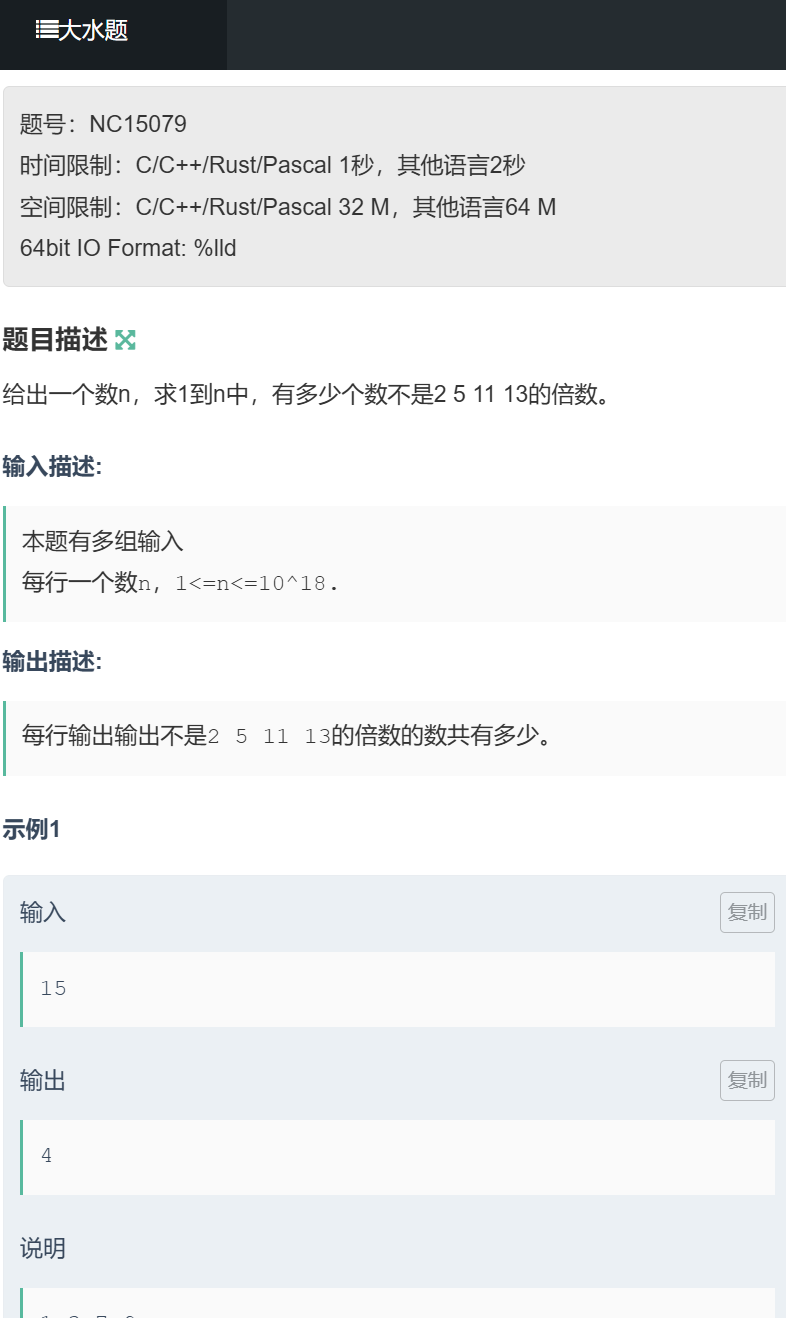
题目描述：给出一个数 n（1≤n≤1e18），求 1 到 n 中不是 2、5、11、13 的倍数的数的个数（多组输入）。

输入示例：15 → 输出示例：4

解题思路：

**反面思考：**总数 - 是 2、5、11、13 中至少一个的倍数的数的个数；

**应用四集合容斥原理：**计算能被 2、5、11、13 中至少一个整除的数的个数，再用 n 减去这个数。

四集合容斥公式：

∣A∪B∪C∪D∣=(∣A∣+∣B∣+∣C∣+∣D∣)−(∣A∩B∣+∣A∩C∣+∣A∩D∣+∣B∩C∣+∣B∩D∣+∣C∩D∣)+(∣A∩B∩C∣+∣A∩B∩D∣+∣A∩C∩D∣+∣B∩C∩D∣)−∣A∩B∩C∩D∣

其中，A 是 2 的倍数集合，B 是 5 的倍数集合，C 是 11 的倍数集合，D 是 13 的倍数集合；

集合交集大小：（lcm 是最小公倍数），多个集合同理。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;
typedef long long LL;

// 计算最大公约数（用于求最小公倍数）
LL gcd(LL a, LL b) {
    return b == 0 ? a : gcd(b, a % b);
}

// 计算最小公倍数
LL lcm(LL a, LL b) {
    return a / gcd(a, b) * b;
}

int main() {
    LL n;
    while (cin >> n) {
        // 四个集合的大小
        LL A = n / 2, B = n / 5, C = n / 11, D = n / 13;
        // 两两交集的大小（6个）
        LL AB = n / lcm(2, 5), AC = n / lcm(2, 11), AD = n / lcm(2, 13);
        LL BC = n / lcm(5, 11), BD = n / lcm(5, 13), CD = n / lcm(11, 13);
        // 三三交集的大小（4个）
        LL ABC = n / lcm(lcm(2, 5), 11), ABD = n / lcm(lcm(2, 5), 13);
        LL ACD = n / lcm(lcm(2, 11), 13), BCD = n / lcm(lcm(5, 11), 13);
        // 四四交集的大小（1个）
        LL ABCD = n / lcm(lcm(2, 5), lcm(11, 13));
        
        // 四集合容斥公式计算至少是一个的倍数的数的个数
        LL cnt = A + B + C + D 
               - (AB + AC + AD + BC + BD + CD) 
               + (ABC + ABD + ACD + BCD) 
               - ABCD;
        
        // 不是任何一个的倍数的数的个数 = 总数 - cnt
        cout << n - cnt << endl;
    }
    return 0;
}

代码解析：

用 gcd 和 lcm 函数计算集合交集的大小（两个数的最小公倍数是它们的乘积除以最大公约数）；

直接套用四集合容斥公式，步骤清晰，适合集合数量较少的场景；

支持 n≤1e18 的超大数，因为所有计算都是除法和加减，无溢出风险（用 long long 存储）。

3.2 例题 2：张老师很强（牛客网）------ 两集合容斥，多组查询

题目链接：https://ac.nowcoder.com/acm/problem/24517

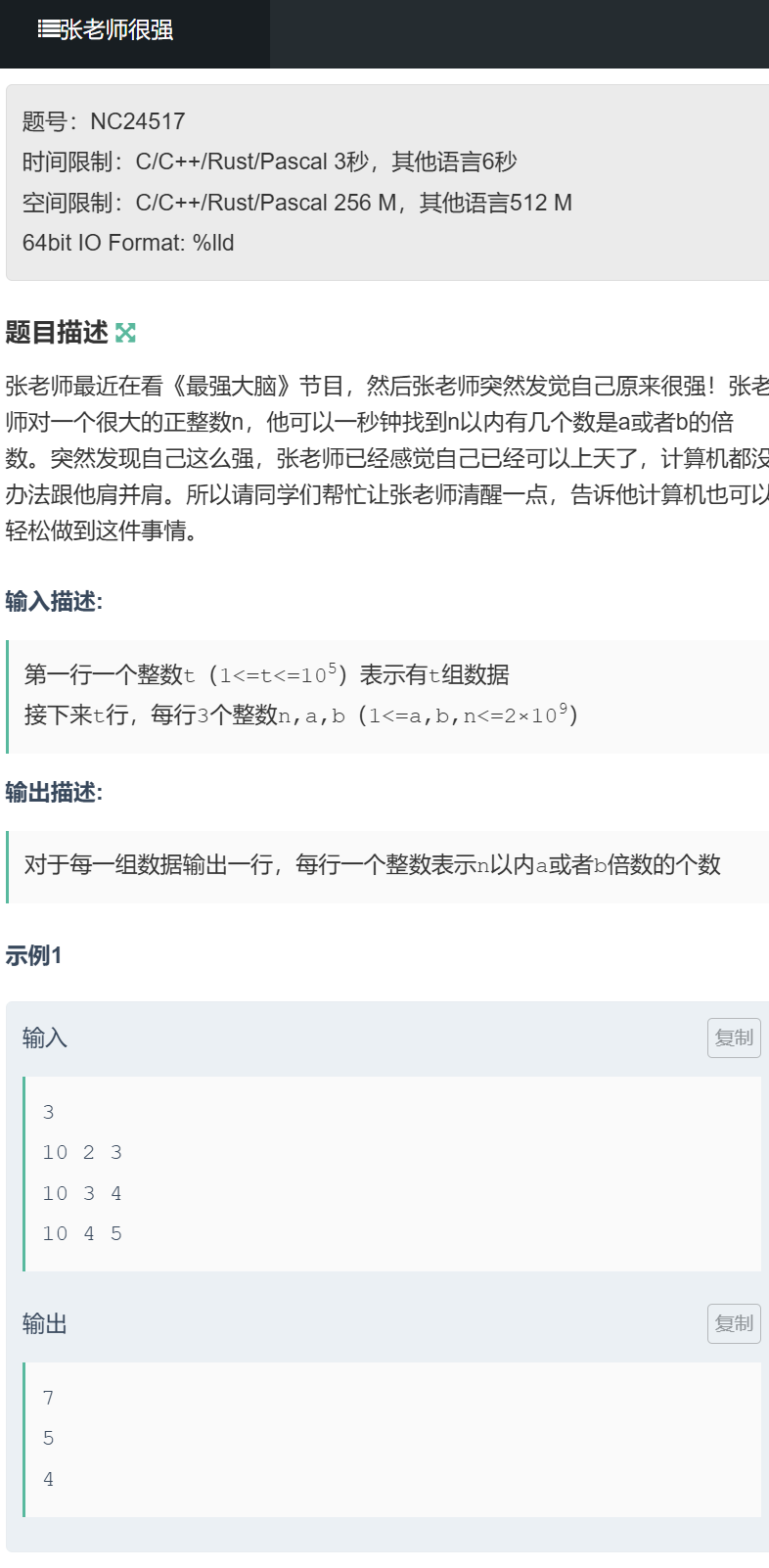
题目描述：t 组数据（1≤t≤1e5），每组给出 n、a、b（1≤a,b,n≤2e9），求 n 以内是 a 或 b 的倍数的数的个数。

输入示例：

10 2 3 → 输出 7

10 3 4 → 输出 5

10 4 5 → 输出 4

解题思路：

直接应用两集合容斥原理：∣A∪B∣=∣A∣+∣B∣−∣A∩B∣；

∣A∣=n/a（a 的倍数个数），∣B∣=n/b（b 的倍数个数），∣A∩B∣=n/lcm(a,b)（a 和 b 的公倍数个数）；

注意 t≤1e5，需要保证每次查询的时间复杂度为 O (1)，不能有多余计算。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;
typedef long long LL;

LL gcd(LL a, LL b) {
    return b == 0 ? a : gcd(b, a % b);
}

LL lcm(LL a, LL b) {
    return a / gcd(a, b) * b;
}

int main() {
    ios::sync_with_stdio(false); // 加速输入输出（应对1e5组数据）
    cin.tie(0);
    int T;
    cin >> T;
    while (T--) {
        LL n, a, b;
        cin >> n >> a >> b;
        LL cnt_a = n / a;
        LL cnt_b = n / b;
        LL cnt_ab = n / lcm(a, b);
        cout << cnt_a + cnt_b - cnt_ab << endl;
    }
    return 0;
}

代码解析：

用**ios::sync_with_stdio(false)和cin.tie(0)**加速输入输出，避免 1e5 组数据超时；

核心逻辑仅 3 行，直接套用两集合容斥公式，简洁高效；

适用于 a、b、n 的范围极大（≤2e9），因为计算量与数值大小无关，仅依赖 gcd 和除法。

3.3 例题 3：集合中的质数（牛客网）------ 二进制枚举，n 集合容斥

题目链接：https://ac.nowcoder.com/acm/problem/14686

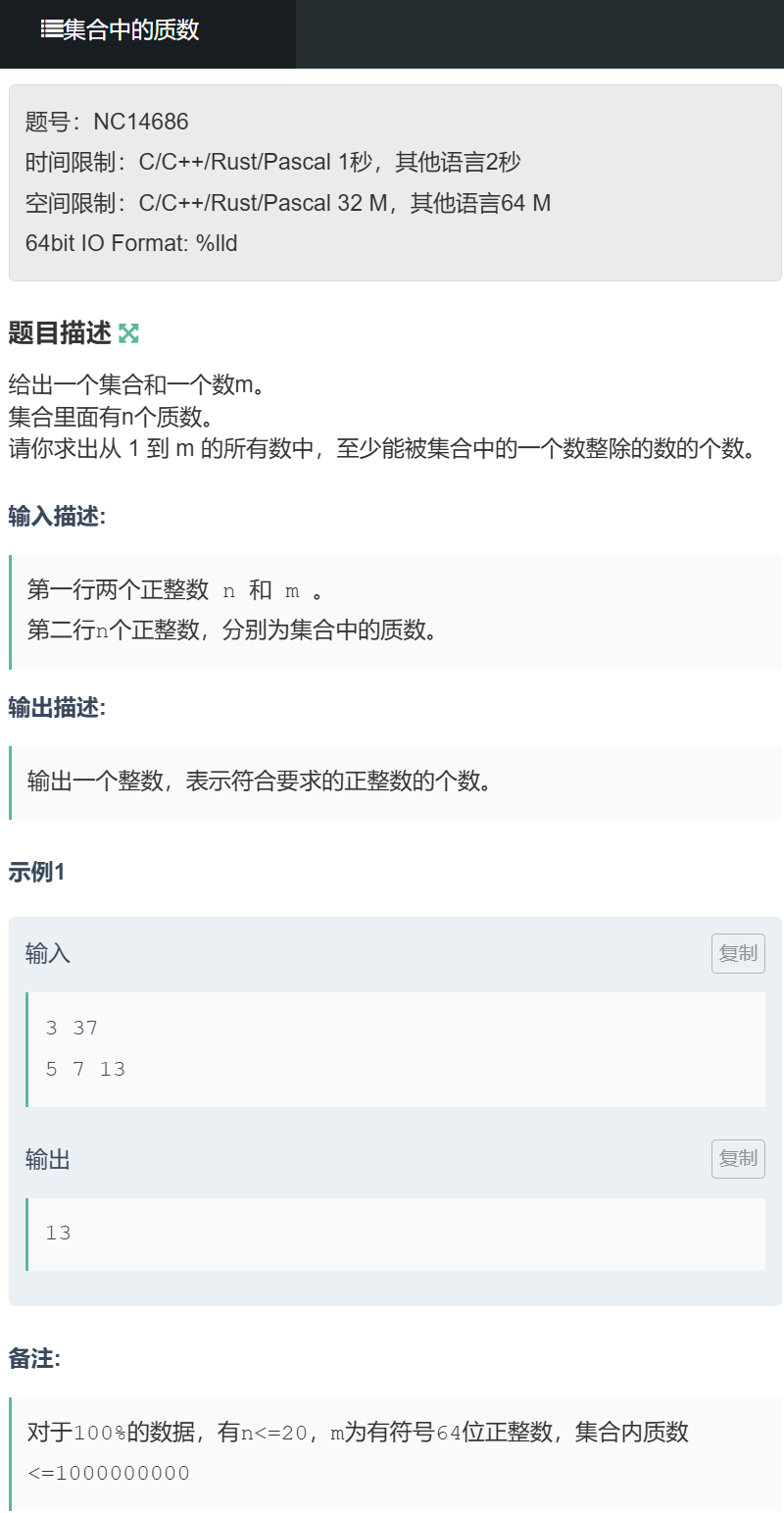
题目描述：给出 n 个质数和 m，求 1 到 m 中至少能被其中一个质数整除的数的个数（1≤n≤20，1≤m≤1e9）。

输入示例：3 375 7 13 → 输出 13

解题思路：

n≤20，直接枚举所有集合组合（2^20=1e6 种，可承受）；

**用二进制枚举所有非空子集：**每个二进制位表示是否选择对应质数；

对于每个子集：

计算子集内所有质数的乘积（即它们的最小公倍数，因为质数互质）；

统计子集大小（二进制中 1 的个数）：奇数个元素则加，偶数个元素则减；

贡献值为 m / 乘积（该子集中所有质数的公倍数个数）。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;
typedef long long LL;

const int N = 30;
LL p[N]; // 存储质数集合

int main() {
    LL n, m;
    cin >> n >> m;
    for (int i = 0; i < n; ++i) {
        cin >> p[i];
    }
    
    LL res = 0;
    // 二进制枚举所有非空子集（st从1到(1<<n)-1）
    for (int st = 1; st < (1 << n); ++st) {
        LL product = 1; // 子集内质数的乘积（LCM）
        int cnt = 0;    // 子集大小（1的个数）
        bool overflow = false; // 是否溢出（乘积超过m）
        
        for (int i = 0; i < n; ++i) {
            if (st >> i & 1) { // 第i位为1，选择该质数
                cnt++;
                // 乘积超过m，后续计算无意义，标记溢出
                if (product > m / p[i]) { 
                    overflow = true;
                    break;
                }
                product *= p[i];
            }
        }
        
        if (overflow) continue;
        // 奇数个元素加，偶数个元素减
        if (cnt % 2 == 1) {
            res += m / product;
        } else {
            res -= m / product;
        }
    }
    
    cout << res << endl;
    return 0;
}

代码解析：

二进制枚举是 n 集合容斥的核心实现方式，适用于 n≤20（2^20=1,048,576 种组合，效率极高）；

加入溢出判断：当质数乘积超过 m 时，m/product 为 0，直接跳过，避免无效计算；

利用质数互质的性质，子集的最小公倍数等于质数乘积，简化计算。

3.4 例题 4：齿轮（洛谷 P6298）------ 容斥 + 组合数，高阶应用

题目链接：https://www.luogu.com.cn/problem/P6298

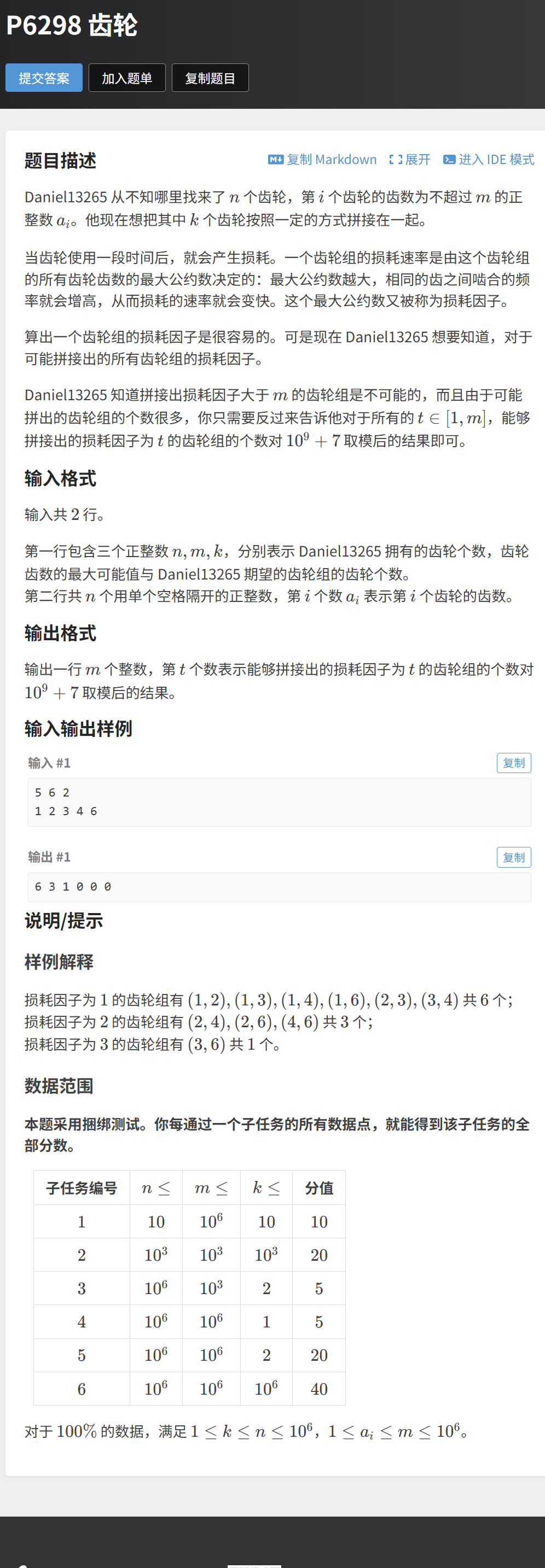
题目描述：n 个齿轮，每个齿轮齿数≤m，选择 k 个齿轮拼接，损耗因子为这 k 个齿轮齿数的最大公约数（gcd）。对于每个 t∈[1,m]，求损耗因子为 t 的齿轮组个数（对 1e9+7 取模）。

输入示例：5 6 21 2 3 4 6 → 输出：6 3 1 0 0 0

解题思路：

**状态定义：**f [t] 表示选择 k 个齿轮，损耗因子恰好为 t 的方案数；

**反向推导：**先计算 "损耗因子是 t 的倍数" 的方案数（记为 g [t]），再用容斥原理减去 "损耗因子是 2t、3t、... 的倍数" 的方案数，得到 f [t]；

**g [t] 的计算：**统计齿数是 t 的倍数的齿轮个数 x，方案数为组合数 C (x, k)（从 x 个中选 k 个）；

容斥逻辑：f [t] = g [t] - f [2t] - f [3t] - ... - f [kt]（k*t ≤m）。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;
typedef long long LL;

const int N = 1e6 + 10;
const int MOD = 1e9 + 7;

LL n, m, k;
int cnt[N]; // cnt[x]表示齿数为x的齿轮个数
LL fac[N], inv[N]; // 阶乘和阶乘逆元（用于计算组合数）
LL f[N]; // f[t]表示损耗因子恰好为t的方案数

// 快速幂（费马小定理求逆元）
LL qpow(LL a, LL b, LL mod) {
    LL res = 1;
    while (b) {
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

// 预处理阶乘和阶乘逆元
void init_fac() {
    fac[0] = 1;
    for (int i = 1; i <= n; ++i) {
        fac[i] = fac[i - 1] * i % MOD;
    }
    inv[n] = qpow(fac[n], MOD - 2, MOD);
    for (int i = n - 1; i >= 0; --i) {
        inv[i] = inv[i + 1] * (i + 1) % MOD;
    }
}

// 计算组合数C(x, k)
LL comb(int x) {
    if (x < k) return 0;
    return fac[x] * inv[k] % MOD * inv[x - k] % MOD;
}

int main() {
    cin >> n >> m >> k;
    for (int i = 0; i < n; ++i) {
        int x;
        cin >> x;
        cnt[x]++;
    }
    
    init_fac();
    
    // 反向计算f[t]：从m到1
    for (int t = m; t >= 1; --t) {
        // 统计齿数是t的倍数的齿轮个数x
        int x = 0;
        for (int j = t; j <= m; j += t) {
            x += cnt[j];
        }
        // g[t] = C(x, k)
        LL g = comb(x);
        // 减去f[2t], f[3t], ...
        for (int j = 2 * t; j <= m; j += t) {
            g = (g - f[j] + MOD) % MOD; // 防止负数
        }
        f[t] = g;
    }
    
    // 输出f[1]到f[m]
    for (int t = 1; t <= m; ++t) {
        cout << f[t] << " ";
    }
    cout << endl;
    
    return 0;
}

代码解析：

反向推导是容斥在 "恰好" 类问题中的经典应用：先求 "至少"（倍数），再减 "多余"（更大的倍数）；

组合数计算依赖阶乘和逆元预处理，支持 n≤1e6，查询 O (1)；

时间复杂度 O (m log m + n)，适合 m≤1e6 的场景。

3.5 例题 5：Devu and Flowers（洛谷 CF451E）------ 容斥 + 隔板法，多重集组合

题目链接：https://www.luogu.com.cn/problem/CF451E

题目描述：n 个花瓶，第 i 个花瓶有 f [i] 朵花，选 s 朵花，求方案数（两种方案不同当且仅当至少一个花瓶选花数量不同），对 1e9+7 取模（1≤n≤20，1≤s≤1e14，1≤f [i]≤1e12）。

解题思路：

**无限制条件：**用隔板法，方案数为 C (s + n - 1, n - 1)（n 个不同盒子放 s 个相同球，允许空盒）；

**限制条件：**每个花瓶最多选 f [i] 朵花，用容斥原理排除 "至少一个花瓶选超过 f [i] 朵" 的非法方案；

容斥逻辑：

二进制枚举子集，标记哪些花瓶超过限制；

对于子集 S，非法方案数为 C (s - sum (f [i]+1) + n - 1, n - 1)（先选 f [i]+1 朵，剩下的无限制）；

子集大小为奇数则减，偶数则加。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;
typedef long long LL;

const int N = 30;
const int MOD = 1e9 + 7;

LL n, s;
LL f[N];
LL inv_fac; // (n-1)! 的逆元

// 快速幂
LL qpow(LL a, LL b) {
    LL res = 1;
    while (b) {
        if (b & 1) res = res * a % MOD;
        a = a * a % MOD;
        b >>= 1;
    }
    return res;
}

// 计算组合数C(x, k)，其中k = n-1（固定）
LL comb(LL x, LL k) {
    if (x < 0 || x < k) return 0;
    LL res = 1;
    // 计算x*(x-1)*...*(x-k+1) / k!
    for (LL i = 0; i < k; ++i) {
        res = res * ((x - i) % MOD) % MOD;
    }
    return res * inv_fac % MOD;
}

int main() {
    cin >> n >> s;
    for (int i = 0; i < n; ++i) {
        cin >> f[i];
    }
    
    LL k = n - 1;
    // 预处理(k)! 的逆元：inv_fac = (k!)^(MOD-2) mod MOD
    LL fac_k = 1;
    for (LL i = 1; i <= k; ++i) {
        fac_k = fac_k * i % MOD;
    }
    inv_fac = qpow(fac_k, MOD - 2);
    
    LL res = 0;
    // 二进制枚举所有子集（包括空集）
    for (int st = 0; st < (1 << n); ++st) {
        LL sum = 0; // 超过限制的花的总数：sum(f[i]+1)
        int cnt = 0; // 子集大小（1的个数）
        
        for (int i = 0; i < n; ++i) {
            if (st >> i & 1) {
                cnt++;
                sum += f[i] + 1;
                if (sum > s) break; // 超出s，非法方案数为0
            }
        }
        
        if (sum > s) continue;
        LL c = comb(s - sum + k, k);
        // 空集（cnt=0）加，奇数减，偶数加
        if (cnt % 2 == 0) {
            res = (res + c) % MOD;
        } else {
            res = (res - c + MOD) % MOD;
        }
    }
    
    cout << res << endl;
    return 0;
}

代码解析：

结合隔板法和容斥原理，解决多重集的组合计数问题；

由于 n≤20，二进制枚举子集（2^20=1e6）效率可行；

组合数计算优化：k=n-1 固定，只需计算分子部分（x*(x-1)...(x-k+1)），再乘分母的逆元，避免处理超大阶乘。

3.6 例题 6：硬币购物（洛谷 P1450）------ 容斥 + 完全背包，动态规划结合

题目链接：https://www.luogu.com.cn/problem/P1450

题目描述：4 种硬币，面值 c1~c4，n 次购物，每次带 d1~d4 枚对应硬币，购买价值 s 的东西，求付款方案数（每种硬币使用不超过 d [i] 枚）。

输入示例：

1 2 5 10 2

3 2 3 1 10 → 输出 4

1000 2 2 2 900 → 输出 27

解题思路：

**无限制条件：**用完全背包计算价值≤s 的付款方案数 f [s]（每种硬币可无限使用）；

**限制条件：**用容斥原理排除 "至少一种硬币使用超过 d [i] 枚" 的非法方案；

容斥逻辑：

二进制枚举 4 种硬币的子集（2^4=16 种，效率极高）；

对于子集 S，非法方案数为f [s - sum ((d [i]+1)*c [i])]（先使用 d [i]+1 枚，剩下的无限制）；

子集大小为奇数则减，偶数则加。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;
typedef long long LL;

const int M = 1e5 + 10;
LL f[M]; // f[j]表示无限制时，价值为j的付款方案数
LL c[4], d[4];

// 完全背包预处理无限制方案数
void init() {
    f[0] = 1;
    for (int i = 0; i < 4; ++i) {
        for (int j = c[i]; j <= 1e5; ++j) {
            f[j] += f[j - c[i]];
        }
    }
}

int main() {
    for (int i = 0; i < 4; ++i) {
        cin >> c[i];
    }
    init();
    
    int n;
    cin >> n;
    while (n--) {
        for (int i = 0; i < 4; ++i) {
            cin >> d[i];
        }
        LL s;
        cin >> s;
        
        LL res = 0;
        // 二进制枚举4种硬币的所有子集（0~15）
        for (int st = 0; st < (1 << 4); ++st) {
            LL sum = 0; // 超过限制的总价值：sum((d[i]+1)*c[i])
            int cnt = 0; // 子集大小
            
            for (int i = 0; i < 4; ++i) {
                if (st >> i & 1) {
                    cnt++;
                    sum += (d[i] + 1) * c[i];
                    if (sum > s) break;
                }
            }
            
            if (sum > s) continue;
            // 奇数减，偶数加
            if (cnt % 2 == 0) {
                res += f[s - sum];
            } else {
                res -= f[s - sum];
            }
        }
        
        cout << res << endl;
    }
    
    return 0;
}

代码解析：

结合动态规划（完全背包）和容斥原理，解决带限制的计数问题；

4 种硬币的子集仅 16 种，每次查询效率极高，适合 n≤1e5 的场景；

完全背包预处理一次，后续查询直接复用，时间复杂度 O (41e5 + n16)，效率拉满。

四、容斥原理的常见误区与避坑指南

4.1 子集枚举遗漏或重复

错误：枚举子集时漏了非空子集，或重复计算某些子集；

解决：用二进制枚举，从 st=1（非空）到 st=(1<<n)-1，确保每个子集仅被枚举一次。

4.2 溢出问题

错误：多个数相乘时超出 long long 范围，导致结果错误；

解决：计算乘积时实时判断是否超过目标值（如 m 或 s），若超过则直接标记溢出，跳过后续计算。

4.3 组合数计算错误

错误：n 或 k 较大时，直接计算组合数导致溢出或超时；

解决：预处理阶乘和逆元，或根据组合数的特点优化计算（如固定 k 时仅计算分子）。

4.4 符号错误

错误：容斥公式中加减符号搞反（奇数个集合应加，偶数个应减）；

解决：牢记 "奇数加，偶数减" 的规律，子集大小为奇数时贡献为正，偶数时为负。

4.5 反向推导顺序错误

错误：在 "恰好" 类问题中，正向计算 f [t] 导致逻辑复杂；

解决：反向推导，先计算 "至少"（倍数），再减去 "多余"（更大的倍数），简化逻辑。

五、容斥原理的拓展应用：不止于集合计数

容斥原理的核心思想可以迁移到很多复杂问题中，例如：

数论问题：统计 1 到 n 中与 m 互质的数的个数（用容斥排除 m 的质因子的倍数）；

排列组合：计算满足多个限制条件的排列数（如元素不能在特定位置）；

动态规划：结合 DP 和容斥，解决带多重限制的计数问题（如硬币购物）；

概率计算：计算多个事件中至少一个发生的概率（用容斥原理转换为交集概率）。

总结

通过本文的学习，你不仅能掌握容斥原理的基本解法，更能理解组合数学中 "化繁为简、补漏去重" 的思维方式。下次遇到重叠计数问题时，不妨先尝试用容斥原理分析，再结合具体场景选择合适的实现方法，轻松解决问题！

如果本文对你有帮助，欢迎点赞、收藏、转发，也欢迎在评论区交流讨论～后续还会分享更多组合数学经典问题，关注我，一起玩转算法！

【算法基础篇】（五十六）容斥原理指南：从集合计数到算法实战，解决组合数学的 “重叠难题”！

目录

前言

一、容斥原理的定义：什么是 "先加后减，补漏去重"？

1.1 核心思想

1.2 从生活案例理解容斥

1.3 数学公式表达

（1）两个集合的容斥原理

（2）三个集合的容斥原理

（3）n 个集合的容斥原理

二、容斥原理的核心应用场景：如何快速识别 "容斥题"？

三、容斥原理的 C++ 实现：6 道例题从入门到高阶

3.1 例题 1：大水题（牛客网）------ 基础容斥，四集合倍数统计

3.2 例题 2：张老师很强（牛客网）------ 两集合容斥，多组查询

3.3 例题 3：集合中的质数（牛客网）------ 二进制枚举，n 集合容斥

3.4 例题 4：齿轮（洛谷 P6298）------ 容斥 + 组合数，高阶应用

3.5 例题 5：Devu and Flowers（洛谷 CF451E）------ 容斥 + 隔板法，多重集组合

3.6 例题 6：硬币购物（洛谷 P1450）------ 容斥 + 完全背包，动态规划结合

四、容斥原理的常见误区与避坑指南

4.1 子集枚举遗漏或重复

4.2 溢出问题

4.3 组合数计算错误

4.4 符号错误

4.5 反向推导顺序错误

五、容斥原理的拓展应用：不止于集合计数

总结