现代密码学【5】之对称加密构造模块

缘友一世2025-12-25 16:57

文章目录

  • PPT(Probabilistic Polynomial Time)：概率多项式时间。

伪随机性

  • 伪随机性是真随机性在计算上的松弛。
  • 利用相对短的密钥生成长的伪随机序列，再以此伪随机序列代替完善保密中要求的长随机密钥，就可以实现接近完善保密的安全性。

伪随机发生器

定义 3.14

令 ℓ ( ⋅ ) \ell(\cdot) ℓ(⋅) 为多项式，令 G G G 为确定多项式时间算法，该算法满足：对于任何输入 s ∈ { 0 , 1 } n s \in \{0,1\}^n s∈{0,1}n，算法 G G G 输出一个长度为 ℓ ( n ) \ell(n) ℓ(n) 的字符串。如果满足下面两个条件，则称 G G G 是一个伪随机发生器：

  1. (扩展性) ：对每个 n n n 来说，满足 ℓ ( n ) > n \ell(n) > n ℓ(n)>n。

  2. (伪随机性) ：对所有的概率多项式时间的区分器 D D D 来说，存在一个可忽略函数 negl \text{negl} negl，满足
    ∣ Pr ⁡ [ D ( r ) = 1 ] − Pr ⁡ [ D ( G ( s ) ) = 1 ] ∣ ≤ negl ( n ) \left| \Pr[D(r) = 1] - \Pr[D(G(s)) = 1] \right| \leq \text{negl}(n) ∣Pr[D(r)=1]−Pr[D(G(s))=1]∣≤negl(n)

    其中 r r r 是从 { 0 , 1 } ℓ ( n ) \{0,1\}^{\ell(n)} {0,1}ℓ(n) 中均匀随机选择的，种子 s s s 是从 { 0 , 1 } n \{0,1\}^n {0,1}n 中均匀随机选择的，并且概率来源为 D D D 的随机性和对 r , s r, s r,s 的选择。

函数 ℓ ( ⋅ ) \ell(\cdot) ℓ(⋅) 被称为 G G G 的扩展系数。

伪随机发生器种子和种子长度

  • 种子和长度。伪随机发生器的种子需均匀随机选取，且对区分器完全保密。 s s s 必须足够长，使蛮力攻击（遍历所有 2 n 2^n 2n 种子）不可行------因算法运行时间多项式， n n n 足够大时无法搜索所有种子，且实际中种子长度固定，故 s s s 需足够长以阻止尝试所有可能种子。

加密方案

  • 一个加密方案被三个算法定义：密钥生成算法Gen，加密算法Enc以及解密算法Dec。加密过程是密钥（作为种子）应用到一个伪随机发生器获取长填充，然后和明文消息异或处理。

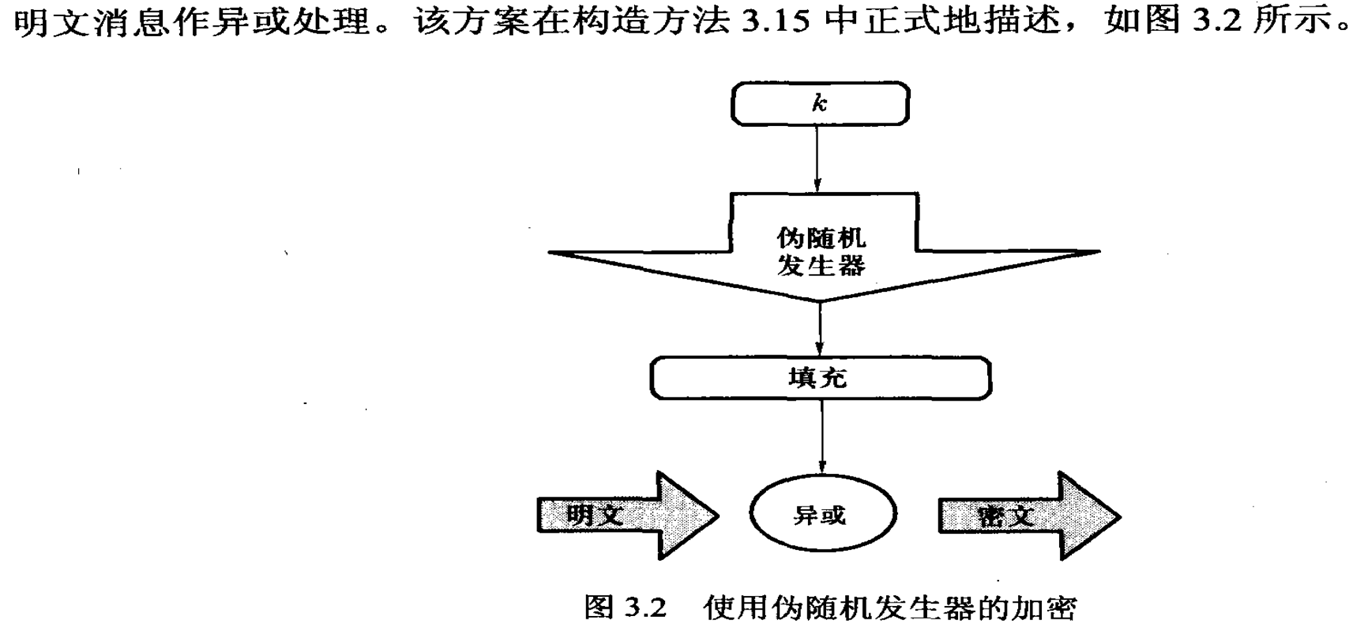
伪随机发生器到安全加密方案

定理 3.16

若 G G G 是一个伪随机发生器，则构造方法 3.15 是一个在窃听者存在的情况下，具备不可区分加密的定长对称密钥加密方案。

定义 3.8

如果对于所有的概率多项式时间对手 A \mathcal{A} A，存在一个可忽略函数 negl \text{negl} negl 使得：
Pr ⁡ [ PrivK A , Π eav ( n ) = 1 ] ≤ 1 2 + negl ( n ) \Pr\left[\text{PrivK}_{\mathcal{A},\Pi}^{\text{eav}}(n) = 1\right] \leq \frac{1}{2} + \text{negl}(n) Pr[PrivKA,Πeav(n)=1]≤21+negl(n)

则一个对称密钥加密方案 Π = ( Gen , Enc , Dec ) \Pi = (\text{Gen}, \text{Enc}, \text{Dec}) Π=(Gen,Enc,Dec) 具备在窃听者存在的情况下不可区分的加密，其中概率的来源是 A \mathcal{A} A 的随机性以及实验的随机性（选择密钥、随机比特 b b b，以及在加密过程中使用到的任何随机性）。

私钥加密的CPA不可区分实验（重点）

CPA 不可区分实验 PrivK A , Π cpa ( n ) \text{PrivK}_{\mathcal{A},\Pi}^{\text{cpa}}(n) PrivKA,Πcpa(n)

  1. 一个密钥 k k k 是通过运行 Gen ( 1 n ) \text{Gen}(1^n) Gen(1n) 生成的。
  2. 输入 1 n 1^n 1n 给 A \mathcal{A} A，敌手 A \mathcal{A} A 可以访问预言机 Enc k ( ⋅ ) \text{Enc}_k(\cdot) Enck(⋅)，输出一对长度相等的信息 m 0 , m 1 m_0, m_1 m0,m1。
  3. 选择一个随机比特 b ← { 0 , 1 } b \leftarrow \{0,1\} b←{0,1}，计算挑战密文 c ← Enc k ( m b ) c \leftarrow \text{Enc}_k(m_b) c←Enck(mb)，交给 A \mathcal{A} A。
  4. 敌手 A \mathcal{A} A 继续访问预言机 Enc k ( ⋅ ) \text{Enc}_k(\cdot) Enck(⋅)，输出一个比特 b ′ b' b′。
  5. 如果 b = b ′ b = b' b=b′，该实验的输出被定义为 1，否则定义为 0。若 PrivK A , Π cpa ( n ) = 1 \text{PrivK}_{\mathcal{A},\Pi}^{\text{cpa}}(n) = 1 PrivKA,Πcpa(n)=1，则认为 A \mathcal{A} A 成功。

定义 3.21

一个对称密钥加密方案 Π = ( Gen , Enc , Dec ) \Pi = (\text{Gen}, \text{Enc}, \text{Dec}) Π=(Gen,Enc,Dec)，如果对所有概率多项式对手 A \mathcal{A} A，存在一个可忽略函数 negl \text{negl} negl，使得
Pr ⁡ [ PrivK A , Π cpa ( n ) = 1 ] ≤ 1 2 + negl ( n ) \Pr\left[\text{PrivK}_{\mathcal{A},\Pi}^{\text{cpa}}(n) = 1\right] \leq \frac{1}{2} + \text{negl}(n) Pr[PrivKA,Πcpa(n)=1]≤21+negl(n)

则称 Π \Pi Π 在选择明文攻击（CPA）条件下的不可区分加密，这里概率来源于 A \mathcal{A} A 使用到的随机性，以及在实验中用到的随机性。

  • 任何方案如果是选择明文攻击条件下的不可区分加密，则也是窃听者存在的情况下不可区分加密。这是因为 P r i v K e a v PrivK^{eav} PrivKeav是 P r i v K c p a PrivK^{cpa} PrivKcpa的一种特殊情况，即敌手没有使用预言机。
  • CPA 安全的加密方案必须是概率性的。必须将随机性作为加密过程中的一部分，来确保相同消息的加密可能是不同的。

伪随机函数

  • 伪随机函数：指将n比特字符串映射到n比特字符串的函数，但是任何固定的函数（没有引入随机性）都不是伪随机函数。

定义 3.23

令 F : { 0 , 1 } ∗ × { 0 , 1 } ∗ → { 0 , 1 } ∗ F: \{0,1\}^* \times \{0,1\}^* \to \{0,1\}^* F:{0,1}∗×{0,1}∗→{0,1}∗ 是有效的、长度保留的、带密钥的函数。如果对所有多项式时间区分器 D D D，存在一个可忽略函数 negl \text{negl} negl，满足：
∣ Pr ⁡ [ D F k ( ⋅ ) ( 1 n ) = 1 ] − Pr ⁡ [ D f ( ⋅ ) ( 1 n ) = 1 ] ∣ ≤ negl ( n ) , \left| \Pr\left[ D^{F_k(\cdot)}(1^n) = 1 \right] - \Pr\left[ D^{f(\cdot)}(1^n) = 1 \right] \right| \leq \text{negl}(n), Pr[DFk(⋅)(1n)=1]−Pr[Df(⋅)(1n)=1] ≤negl(n),

则称 F F F 是一个伪随机函数，其中 k ← { 0 , 1 } n k \leftarrow \{0,1\}^n k←{0,1}n 是均匀随机选择的，并且 f f f 是从将 n n n 比特字符串映射到 n n n 比特字符串的函数集合中均匀随机选择出来的。

基于伪随机函数CPA加密实验（重点）

构造方法 3.24

令 F F F 是伪随机函数，定义一个消息长度为 n n n 的对称密钥加密方案如下：

  • Gen ：输入 1 n 1^n 1n，均匀随机地选择 k ← { 0 , 1 } n k \leftarrow \{0,1\}^n k←{0,1}n，并将其作为密钥输出。
  • Enc ：输入一个密钥 k ∈ { 0 , 1 } n k \in \{0,1\}^n k∈{0,1}n，以及一个消息 m ∈ { 0 , 1 } n m \in \{0,1\}^n m∈{0,1}n，均匀随机地选择 r ← { 0 , 1 } n r \leftarrow \{0,1\}^n r←{0,1}n，并且输出密文
    c : = ⟨ r , F k ( r ) ⊕ m ⟩ . c := \langle r, F_k(r) \oplus m \rangle. c:=⟨r,Fk(r)⊕m⟩.
  • Dec ：输入一个密钥 k ∈ { 0 , 1 } n k \in \{0,1\}^n k∈{0,1}n，以及一个密文 c = ⟨ r , s ⟩ c = \langle r, s \rangle c=⟨r,s⟩，输出明文消息
    m : = F k ( r ) ⊕ s . m := F_k(r) \oplus s. m:=Fk(r)⊕s.
    从任意伪随机函数构造CPA安全的加密方案。

定理 3.25

如果 F F F 是伪随机函数，则构造方法 3.24 为消息长度为 n n n 的定长对称密钥加密方案，在选择明文攻击下，该构造方法具备不可区分加密。

CPA安全加密证明（重点）

要证明基于伪随机函数（PRF）的对称加密方案在选择明文攻击（CPA）下具备不可区分加密（IND-CPA）安全性，核心思路是规约（Reduction） ：将敌手（Adversary） A \mathcal{A} A 对加密方案的攻击能力，转化为区分器（Distinguisher） D D D 对伪随机函数的区分能力。

证明目标

若伪随机函数 F F F 是安全的（即无法被多项式时间区分器区分于随机函数），则构造方法3.24（基于 F F F的加密方案）是IND-CPA安全的。

关键概念

  • 加密方案 ： Π = ( Gen , Enc , Dec ) \Pi = (\text{Gen}, \text{Enc}, \text{Dec}) Π=(Gen,Enc,Dec)，其中 Enc \text{Enc} Enc使用 F k ( r ) ⊕ m F_k(r) \oplus m Fk(r)⊕m生成密文（ r r r为随机数， k k k为密钥）。
  • 伪随机函数（PRF） ： F k ( ⋅ ) F_k(\cdot) Fk(⋅)的输出与随机函数 f ( ⋅ ) f(\cdot) f(⋅)的输出无法被区分（定义3.23）。
  • IND-CPA实验 ：敌手 A \mathcal{A} A可询问加密预言机（ Enc k ( ⋅ ) \text{Enc}_k(\cdot) Enck(⋅)），最终猜测挑战密文的明文比特 b b b（成功概率需接近 1 / 2 1/2 1/2）。

证明步骤（简化版）

1. 构造"理想"加密方案 Π ~ \widetilde{\Pi} Π

  • 用随机函数 f f f（而非 F k F_k Fk）替代 F k F_k Fk，定义 Π ~ = ( Gen ~ , Enc ~ , Dec ~ ) \widetilde{\Pi} = (\widetilde{\text{Gen}}, \widetilde{\text{Enc}}, \widetilde{\text{Dec}}) Π =(Gen ,Enc ,Dec )：
    • Gen ~ ( 1 n ) \widetilde{\text{Gen}}(1^n) Gen (1n)：选择随机函数 f ← Func n f \leftarrow \text{Func}_n f←Funcn（ Func n \text{Func}_n Funcn为所有 n n n比特到 n n n比特的函数集合）。
    • Enc ~ \widetilde{\text{Enc}} Enc ：与 Enc \text{Enc} Enc相同，即 c = ⟨ r , f ( r ) ⊕ m ⟩ c = \langle r, f(r) \oplus m \rangle c=⟨r,f(r)⊕m⟩（ r ← { 0 , 1 } n r \leftarrow \{0,1\}^n r←{0,1}n）。
    • Dec ~ \widetilde{\text{Dec}} Dec ：与 Dec \text{Dec} Dec相同，即 m = f ( r ) ⊕ s m = f(r) \oplus s m=f(r)⊕s（ c = ⟨ r , s ⟩ c = \langle r, s \rangle c=⟨r,s⟩）。
      注： Π ~ \widetilde{\Pi} Π 是"无效"方案（因 f f f无密钥），但用于证明假设。

2. 分析 A \mathcal{A} A对 Π ~ \widetilde{\Pi} Π 的成功概率

敌手 A \mathcal{A} A在 Π ~ \widetilde{\Pi} Π 的IND-CPA实验中，成功概率满足：
Pr ⁡ [ PrivK A , Π ~ cpa ( n ) = 1 ] ≤ 1 2 + q ( n ) 2 n (1) \Pr\left[\text{PrivK}_{\mathcal{A},\widetilde{\Pi}}^{\text{cpa}}(n) = 1\right] \leq \frac{1}{2} + \frac{q(n)}{2^n} \tag{1} Pr[PrivKA,Π cpa(n)=1]≤21+2nq(n)(1)

其中 q ( n ) q(n) q(n)是 A \mathcal{A} A的运行时间（多项式）， q ( n ) 2 n \frac{q(n)}{2^n} 2nq(n)是 A \mathcal{A} A"重复使用"挑战密文随机数 r c r_c rc的概率（因 r c r_c rc被预言机使用时， A \mathcal{A} A可推断明文，否则猜测 b b b的概率为 1 / 2 1/2 1/2）。

3. 构造PRF区分器 D D D

用 A \mathcal{A} A构造区分器 D D D，目标：区分 F k ( ⋅ ) F_k(\cdot) Fk(⋅)（伪随机）与 f ( ⋅ ) f(\cdot) f(⋅)（随机）。

  • D D D的输入： 1 n 1^n 1n，可访问预言机 O : { 0 , 1 } n → { 0 , 1 } n \mathcal{O}: \{0,1\}^n \to \{0,1\}^n O:{0,1}n→{0,1}n（ F k F_k Fk或 f f f）。
  • D D D的行为：
    1. 运行 A ( 1 n ) \mathcal{A}(1^n) A(1n)，模拟 Π ~ \widetilde{\Pi} Π 的加密预言机：
      • 当 A \mathcal{A} A询问消息 m m m时， D D D选择 r ← { 0 , 1 } n r \leftarrow \{0,1\}^n r←{0,1}n，查询 O ( r ) \mathcal{O}(r) O(r)得 s ′ s' s′，返回 c = ⟨ r , s ′ ⊕ m ⟩ c = \langle r, s' \oplus m \rangle c=⟨r,s′⊕m⟩。
    2. 当 A \mathcal{A} A输出 m 0 , m 1 m_0, m_1 m0,m1时， D D D选择 b ← { 0 , 1 } b \leftarrow \{0,1\} b←{0,1}，选择 r ← { 0 , 1 } n r \leftarrow \{0,1\}^n r←{0,1}n，查询 O ( r ) \mathcal{O}(r) O(r)得 s ′ s' s′，返回挑战密文 c = ⟨ r , s ′ ⊕ m b ⟩ c = \langle r, s' \oplus m_b \rangle c=⟨r,s′⊕mb⟩。
    3. A \mathcal{A} A输出 b ′ b' b′，若 b ′ = b b' = b b′=b， D D D输出1（认为 O \mathcal{O} O是 F k F_k Fk）；否则输出0（认为 O \mathcal{O} O是 f f f）。

4. 分析 D D D的成功概率

  • 若 O \mathcal{O} O是 F k ( ⋅ ) F_k(\cdot) Fk(⋅)（伪随机）：
    D D D的视图与 A \mathcal{A} A在 Π \Pi Π的IND-CPA实验中相同（因 F k F_k Fk的输出与 f f f的输出无法区分），故：
    Pr ⁡ [ D F k ( ⋅ ) ( 1 n ) = 1 ] = Pr ⁡ [ PrivK A , Π cpa ( n ) = 1 ] (2) \Pr\left[D^{F_k(\cdot)}(1^n) = 1\right] = \Pr\left[\text{PrivK}_{\mathcal{A},\Pi}^{\text{cpa}}(n) = 1\right] \tag{2} Pr[DFk(⋅)(1n)=1]=Pr[PrivKA,Πcpa(n)=1](2)
  • 若 O \mathcal{O} O是 f ( ⋅ ) f(\cdot) f(⋅)（随机）：
    D D D的视图与 A \mathcal{A} A在 Π ~ \widetilde{\Pi} Π 的IND-CPA实验中相同，故：
    Pr ⁡ [ D f ( ⋅ ) ( 1 n ) = 1 ] = Pr ⁡ [ PrivK A , Π ~ cpa ( n ) = 1 ] (3) \Pr\left[D^{f(\cdot)}(1^n) = 1\right] = \Pr\left[\text{PrivK}_{\mathcal{A},\widetilde{\Pi}}^{\text{cpa}}(n) = 1\right] \tag{3} Pr[Df(⋅)(1n)=1]=Pr[PrivKA,Π cpa(n)=1](3)

5. 结合(1)(2)(3)得出结论

将(2)(3)代入(1)，得：
Pr ⁡ [ D F k ( ⋅ ) ( 1 n ) = 1 ] − Pr ⁡ [ D f ( ⋅ ) ( 1 n ) = 1 ] ≥ ε ( n ) − q ( n ) 2 n \Pr\left[D^{F_k(\cdot)}(1^n) = 1\right] - \Pr\left[D^{f(\cdot)}(1^n) = 1\right] \geq \varepsilon(n) - \frac{q(n)}{2^n} Pr[DFk(⋅)(1n)=1]−Pr[Df(⋅)(1n)=1]≥ε(n)−2nq(n)

其中 ε ( n ) = Pr ⁡ [ PrivK A , Π cpa ( n ) = 1 ] − 1 2 \varepsilon(n) = \Pr\left[\text{PrivK}_{\mathcal{A},\Pi}^{\text{cpa}}(n) = 1\right] - \frac{1}{2} ε(n)=Pr[PrivKA,Πcpa(n)=1]−21（ A \mathcal{A} A对 Π \Pi Π的优势）。

因 F F F是PRF（无法被 D D D区分），故 ε ( n ) − q ( n ) 2 n \varepsilon(n) - \frac{q(n)}{2^n} ε(n)−2nq(n)是可忽略的 （ q ( n ) q(n) q(n)是多项式）。因此 ε ( n ) \varepsilon(n) ε(n)是可忽略的，即 Π \Pi Π是IND-CPA安全的。

简答题参考答案（分步骤）

问题 ：简述基于伪随机函数的加密方案在CPA下安全的证明过程。
答案：

  1. 构造理想方案 ：用随机函数 f f f替代伪随机函数 F k F_k Fk，定义无效加密方案 Π ~ \widetilde{\Pi} Π ，分析敌手 A \mathcal{A} A对 Π ~ \widetilde{\Pi} Π 的成功概率（ ≤ 1 / 2 + q ( n ) / 2 n \leq 1/2 + q(n)/2^n ≤1/2+q(n)/2n）。
  2. 构造区分器 ：用 A \mathcal{A} A构造PRF区分器 D D D，模拟 Π ~ \widetilde{\Pi} Π 的加密预言机，将 A \mathcal{A} A的攻击转化为 D D D对 F k F_k Fk与 f f f的区分。
  3. 分析区分器概率 ：若 D D D的预言机是 F k F_k Fk，其成功概率等于 A \mathcal{A} A对 Π \Pi Π的成功概率；若预言机是 f f f，其成功概率等于 A \mathcal{A} A对 Π ~ \widetilde{\Pi} Π 的成功概率。
  4. 得出结论 ：结合 Π ~ \widetilde{\Pi} Π 的成功概率，若 F F F是PRF（无法被 D D D区分），则 A \mathcal{A} A对 Π \Pi Π的优势是可忽略的，故 Π \Pi Π是CPA安全的。

选择密文攻击（重点）

  • 选择密文攻击(CCA)：敌手不仅具有加密消息的能力（加密预言机），还具有解密密文的能力（解密预言机）。

CCA的不可区分实验

CCA 不可区分实验 PrivK A , Π cca ( n ) \text{PrivK}_{\mathcal{A},\Pi}^{\text{cca}}(n) PrivKA,Πcca(n)

  1. 通过运行 Gen ( 1 n ) \text{Gen}(1^n) Gen(1n) 生成一个密钥 k k k。
  2. 敌手 A \mathcal{A} A 被指定输入 1 n 1^n 1n，可使用预言机 Enc k ( ⋅ ) \text{Enc}_k(\cdot) Enck(⋅) 和 Dec k ( ⋅ ) \text{Dec}_k(\cdot) Deck(⋅)。它输出一对长度相等的消息 m 0 , m 1 m_0, m_1 m0,m1。
  3. 随机选择比特 b ← { 0 , 1 } b \leftarrow \{0,1\} b←{0,1}，则计算密文 c ← Enc k ( m b ) c \leftarrow \text{Enc}_k(m_b) c←Enck(mb) 并将其提供给 A \mathcal{A} A。我们把 c c c 叫做挑战密文。
  4. 敌手 A \mathcal{A} A 继续使用预言机 Enc k ( ⋅ ) \text{Enc}_k(\cdot) Enck(⋅) 和 Dec k ( ⋅ ) \text{Dec}_k(\cdot) Deck(⋅)，但是不允许用挑战密文本身来问询 Dec k ( ⋅ ) \text{Dec}_k(\cdot) Deck(⋅)。最终， A \mathcal{A} A 输出一个比特 b ′ b' b′。
  5. 如果 b ′ = b b' = b b′=b，实验的输出为 1，否则输出 0。

定义 3.30

一个对称密钥加密方案 Π \Pi Π 满足如下条件：对所有的概率多项式时间敌手 A \mathcal{A} A，存在一个可忽略的函数 negl \text{negl} negl，使得
Pr ⁡ [ PrivK A , Π cca ( n ) = 1 ] ≤ 1 2 + negl ( n ) \Pr\left[\text{PrivK}_{\mathcal{A},\Pi}^{\text{cca}}(n) = 1\right] \leq \frac{1}{2} + \text{negl}(n) Pr[PrivKA,Πcca(n)=1]≤21+negl(n)

则称其为选择密文攻击条件下不可区分加密（或者是 CCA 安全的）其中概率来源于实验中的所有随机因素。

相关推荐
网安INF7 小时前
电子邮件的系统架构和核心协议详解
网络·网络协议·安全·网络安全·密码学·电子邮件
岁岁的O泡奶9 小时前
NSSCTF_crypto_[SWPU 2020]happy
经验分享·python·算法·密码学
缘友一世13 小时前
现代密码学【4】之计算安全性&安全规约证明&对称加密的窃听不可区分实验
安全·密码学
网安INF1 天前
SSL/TLS密钥派生机制与安全攻防体系深度解析
网络·安全·网络安全·密码学·ssl
网安INF1 天前
SSL/TLS协议深度解析：记录、警报与握手
网络·网络协议·安全·网络安全·密码学·ssl
缘友一世2 天前
现代密码学【2】之古典密码学
密码学
缘友一世2 天前
现代密码学【1】之密码学概述
密码学
缘友一世2 天前
现代密码学【3】之密码学形式化分析与可证明安全基础
安全·密码学·概率论
天若有情6736 天前
我发明的PROTO_V4协议：一个让数据“穿上迷彩服”的发明（整数传输协议）
网络·c++·后端·安全·密码学·密码·数据
热门推荐
01GitHub 镜像站点023D 圣诞树网页代码03从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击04UV安装并设置国内源05Gemini3 生成的基于手势控制3D粒子圣诞树06Linux下V2Ray安装配置指南07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题09GLM-4.7 vs MiniMax-M2.1：代码工程理解10开源分享 | 超浪漫 3D 圣诞树立体动画（附零基础使用教程）