图像缩放
图像的缩放(Image Scaling)是指通过调整图像的像素数量来改变图像的尺寸。在缩放过程中,图像的宽度和高度可以按一定比例增加或减少。
图像缩放的原理是根据需要将原图像的像素数量增加或减少。
void resize(InputArray src, OutputArray dst, Size dsize,
double fx = 0, double fy = 0, int interpolation = INTER_LINEAR);
//src:代表需要缩放的原始图像
//dst: 代表输出的目标图像,该图像的类型与src相同,其大小为dsize(当该值非零时),或者可以通过
src.size()、fx、fy 计算得到
//dsize:代表输出图像大小
//fx:水平方向的缩放比例
//fy:垂直方向的缩放比例
//interpolation 代表插值方式,默认使用双线性插值法
在resize()函数中,目标图像的大小可以通过 "参数dsize" 或者 "参数fx和fy" 二者之一来指定。若两个参数都写,默认通过dsize改变图像大小。
图片镜像翻转
图像的镜像翻转是以图像的中心轴为基准进行的翻转操作。
void flip(InputArray src, OutputArray dst, int flipCode);
//src:代表要处理的原始图像。
//flipCode:代表旋转类型。
//dst:代表和原始图像具有同样大小、类型的目标图像。
图片镜像旋转组件里的参数flipcode有三个选择:
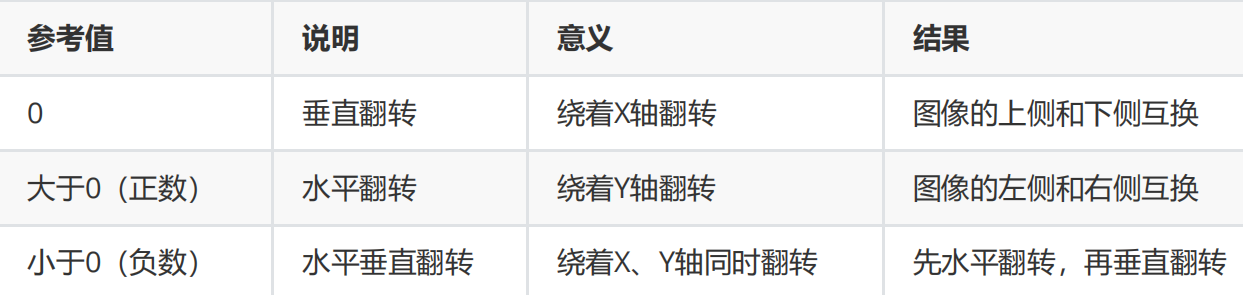
图像仿射变换
仿射变换是指图像可以通过一系列的几何变换来实现平移、旋转等多种操作。该变换能够保持图像的平直性和平行性。平直性是指图像经过仿射变换后,直线仍然是直线; 平行性是指图像在完成仿射变换后,平行线仍然是平行线。
OpenCV 中的仿射函数为warpAffine(),其通过一个变换矩阵(映射矩阵)M 实现变换,具体为:
目标图像 = 变换矩阵M * 原始图像
void warpAffine(
InputArray src, // 输入图像
OutputArray dst, // 输出图像
InputArray M, // 仿射变换矩阵2*3
Size dsize, // 输出图像的尺寸
int flags = INTER_LINEAR, // 插值方法(可选)
int borderMode = BORDER_CONSTANT, // 边界模式(可选)
const Scalar &borderValue = Scalar() // 边界颜色(可选)
);
图片平移
通过转换矩阵M实现将原始图像src转换为目标图像dst :
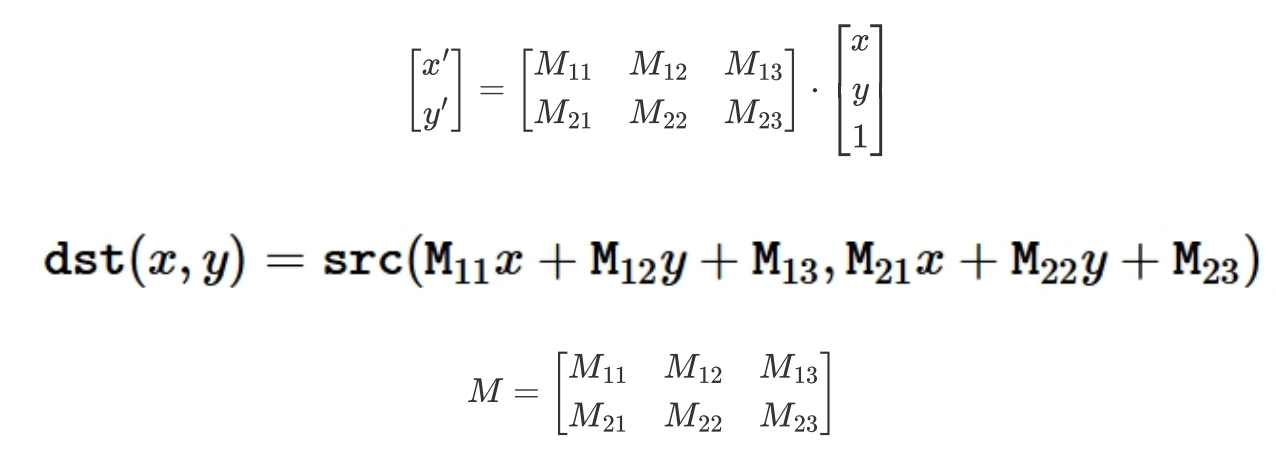
将原始图像src向右侧移动100个像素、向下方移动100个像素,则其对应关系为:
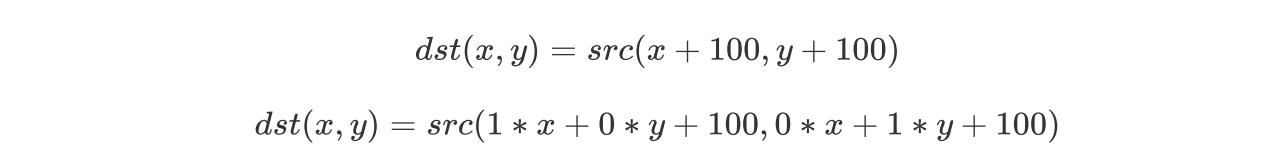
根据上述表达式,可以确定对应的转换矩阵M中各个元素的值为:

在已知转换矩阵M的情况下,可以直接利用转换矩阵M调用函数 warpAfine()完成图像的平移。
图片旋转
在OpenCV中,我们可以使用 getRotationMatrix2D() 函数来生成一个用于旋转图像的"变换矩阵"。
Mat getRotationMatrix2D(
Point2f center,
double angle,
double scale
);
//center: 旋转中心点。指定图像中哪个点为旋转的中心。
//angle: 旋转角度。以度数表示。角度为正数时,图像逆时针旋转;角度为负数时,图像顺时针旋
转。
//scale: 缩放因子。旋转图像时对图像进行缩放。大于1表示放大,小于1表示缩小。
复杂的仿射变换
对于更复杂仿射变换,OpenCV 提供了函数 getAffineTransform()来生成仿射函数warpAffine()所使用的转换矩阵M。该函数的语法格式为:
Mat getAffineTransform(const Point2f src[], const Point2f dst[]);
//const Point2f src[]:输入图像中选取的 3 个点的坐标(作为变换前的点)。
//const Point2f dst[]:输出图像中 3 个点的新坐标(作为变换后的点)。
插值方法
问题背景:旋转过程中的信息丢失,缩放过程中的信息丢失。
**插值(Interpolation)**是一种通过已知数据点之间的推断或估计来获取新数据点的方法。
作用:根据已知的像素值来推测未知位置的像素值。
2****种常见的插值算法: 最近邻插值(Nearest Neighbor Interpolation),双线性插值(Bilinear Interpolation)。
目标点与原图像点之间坐标的计算公式:
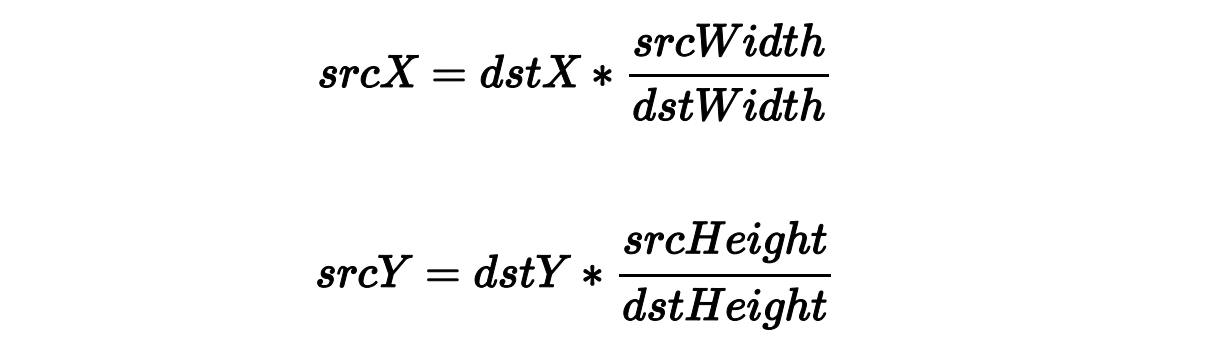
坐标关系:
目标图像中的坐标:
dstX :目标图像中某点的 x 坐标。 dstY :目标图像中某点的 y 坐标。
原图像的尺寸:
srcWidth :原图的宽度。 srcHeight :原图的高度。
目标图像的尺寸:
dstWidth :目标图像的宽度。 dstHeight :目标图像的高度。
原图像中的坐标:
srcX :目标图像中某点对应的原图中点的 x 坐标。 srcY :目标图像中某点对应的原图
中点的 y 坐标。
映射关系:
为了在目标图像中计算每个像素的值,需要根据插值方法找到原图像中对应的像素值。
公式或方法的目的是让目标图像中的每个像素值都能找到原图像中的对应像素值,从而根据不
同的插值方法获取新像素值。
线性插值
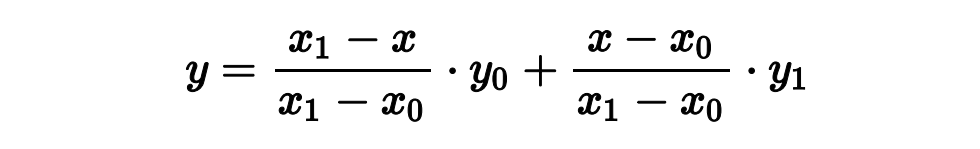
公式是两点之间计算距离,并把这个距离作为权重,用来加权求和两个点的 y 值。
双线性插值
双线性插值本质上就是在两个方向上分别进行线性插值。
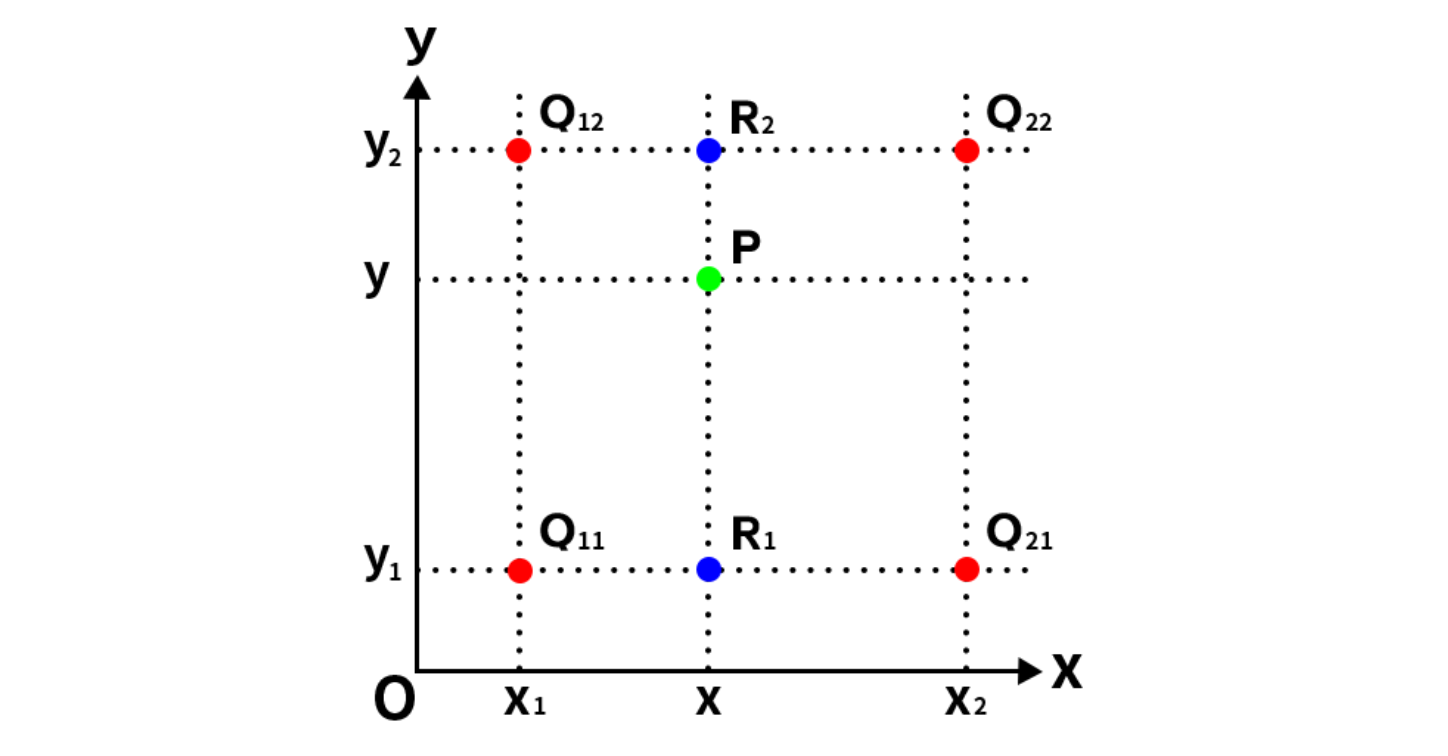
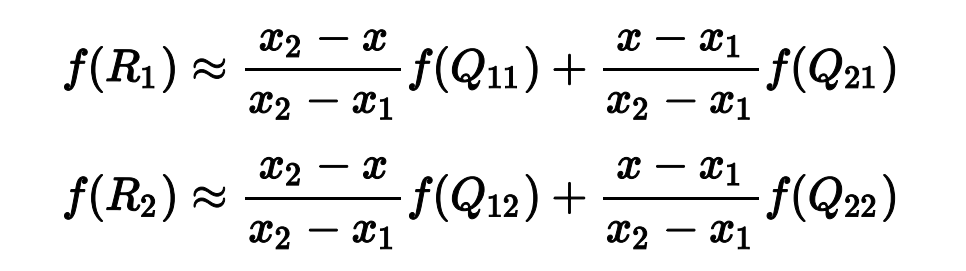
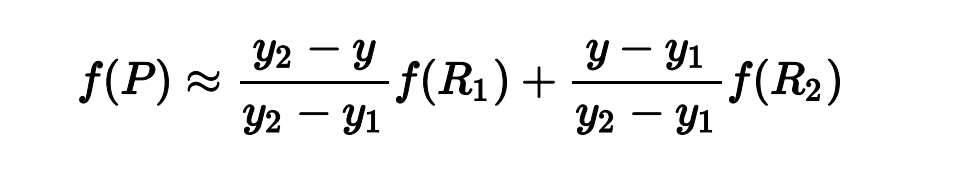
在OpenCV中,关于插值方法默认选择的都是双线性插值,且一般情况下双线性插值已经能满足
大部分需求。
边界复制(BORDER_REPLICATE)
边界复制会将边界处的像素值进行复制,然后作为边界填充的像素值,如下图所示,可以看到四周的像素值都一样。

边界反射(BORDER_REFLECT)
如下图所示,会根据原图的边缘进行反射。

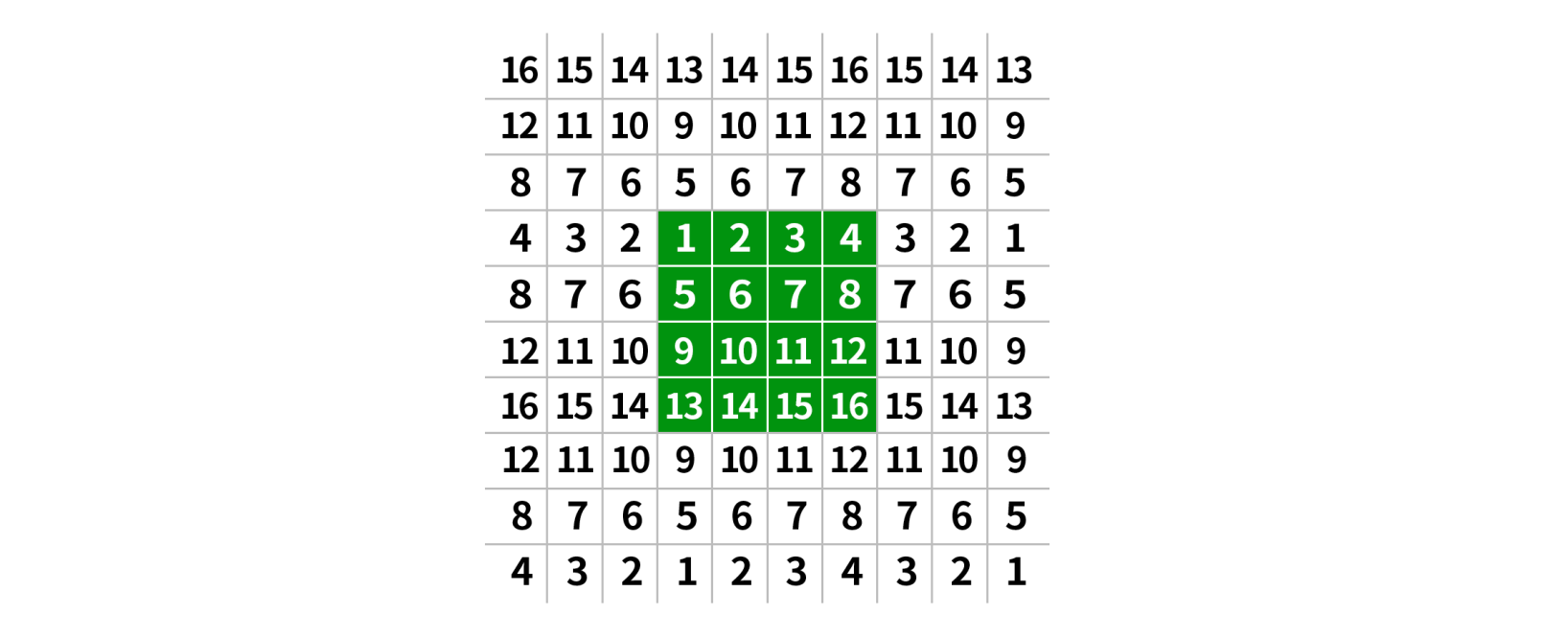
边界反射101(BORDER_REFLECT_101)
与边界反射不同的是,不再反射边缘的像素点,如下图所示。
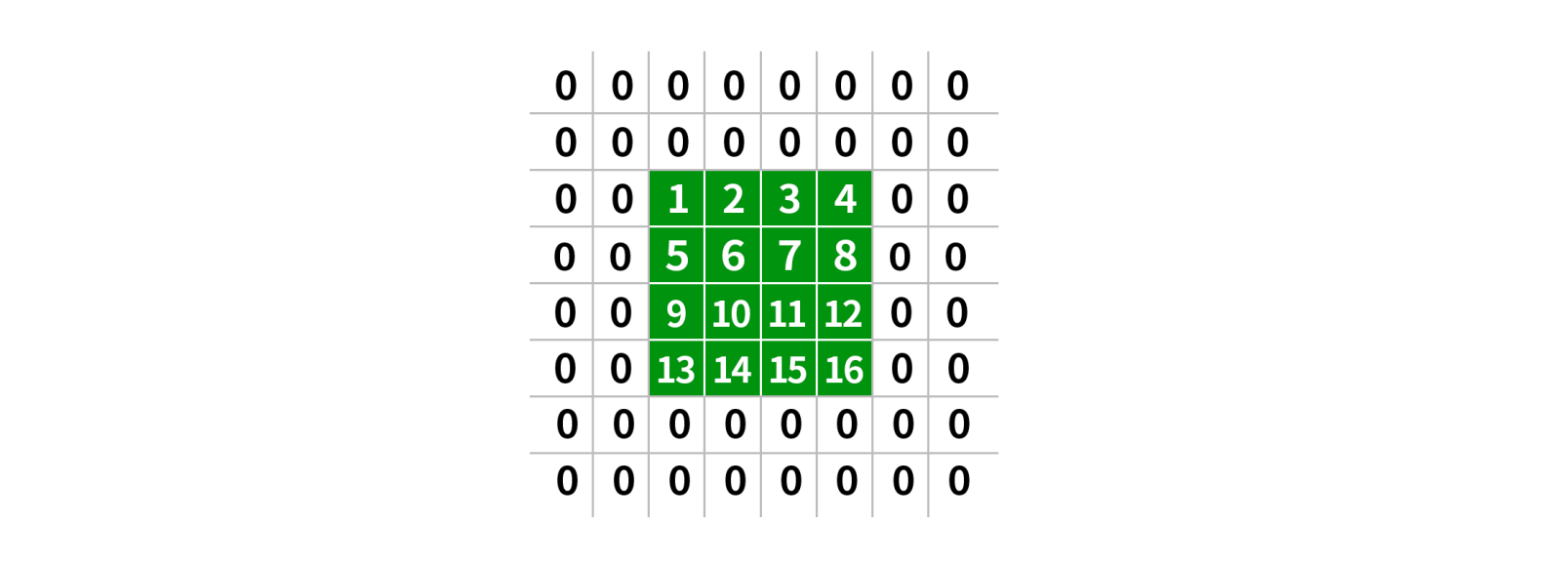
边界常数(BORDER_CONSTANT)
当选择边界常数时,还要指定常数值是多少,默认的填充常数值为0,如下图所示。
边界包裹(BORDER_WRAP)

图像矫正
图像矫正的原理是透视变换。
仿射变换是把一个二维坐标系转换到另一个二维坐标系的过程,转换过程坐标点的相对位置和属性不发生变换,是一个线性变换,该过程只发生旋转和平移过程。
而透视变换是把一个图像投影到一个新的视平面的过程。
透视投影是指将三维空间中的物体投影到二维平面上的过程,这个过程会导致物体在图像中出现形变和透视畸变。透视变换可以通过数学模型来校正这种透视畸变,使得图像中的物体看起来更符合我们的直观感受。
与仿射变换一样,透视变换也有自己的透视变换矩阵:
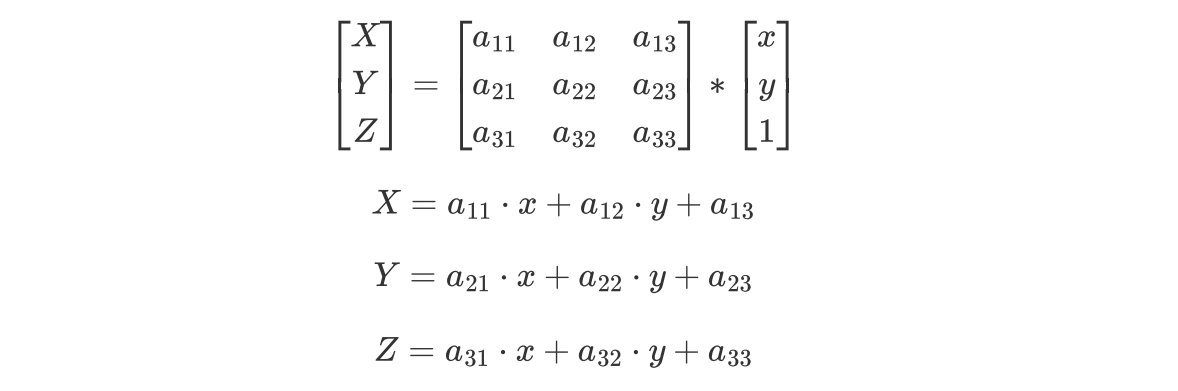
由此可得新的坐标的表达式为:

其中x、y是原始图像点的坐标,x'和y'是变换后的坐标,a11,a12,...,a33则是一些透视变换矩阵的系数。
OpenCV里也提供了getPerspectiveTransform()函数用来生成该3*3的透视变换矩阵。
用于将图像中的点从原来的位置移动到新的位置,从而实现透视效果。
Mat getPerspectiveTransform (const Point2f src[],
const Point2f dst[],
int solveMethod = DECOMP_LU )
//src:源图像中的四个点坐标。
//dst:透视变换后,src的四个点在新目标图像的四个新坐标。
//返回值:返回一个 Mat 对象透视变换矩阵。
得到透视变化矩阵之后,使用warpPerspective()函数即可进行透视变化计算,并得到新的图像。
void warpPerspective (InputArray src,
OutputArray dst,
InputArray M,
Size dsize,
int flags = INTER_LINEAR,
int borderMode = BORDER_CONSTANT,
const Scalar & borderValue = Scalar()
)
src:输入图像。
dst:输出图像,类型和输入图像相同。
M:透视变换矩阵。
dsize:输出图像的大小。
flags:插值方法的标记。
borderMode:边界填充的模式。
borderValue:边界填充值。