美赛备战：数学建模中的微分方程问题2.Python代码实现

几种常见微分方程的详细原理在上一篇文章里已经讲述了，文章链接：https://blog.csdn.net/qq_53529450/article/details/155395031?fromshare=blogdetail&sharetype=blogdetail&sharerId=155395031&sharerefer=PC&sharesource=qq_53529450&sharefrom=from_link 这篇文章直接提供代码，具体问题中只需要修改初始值。

一、生长曲线对比：指数、logistic

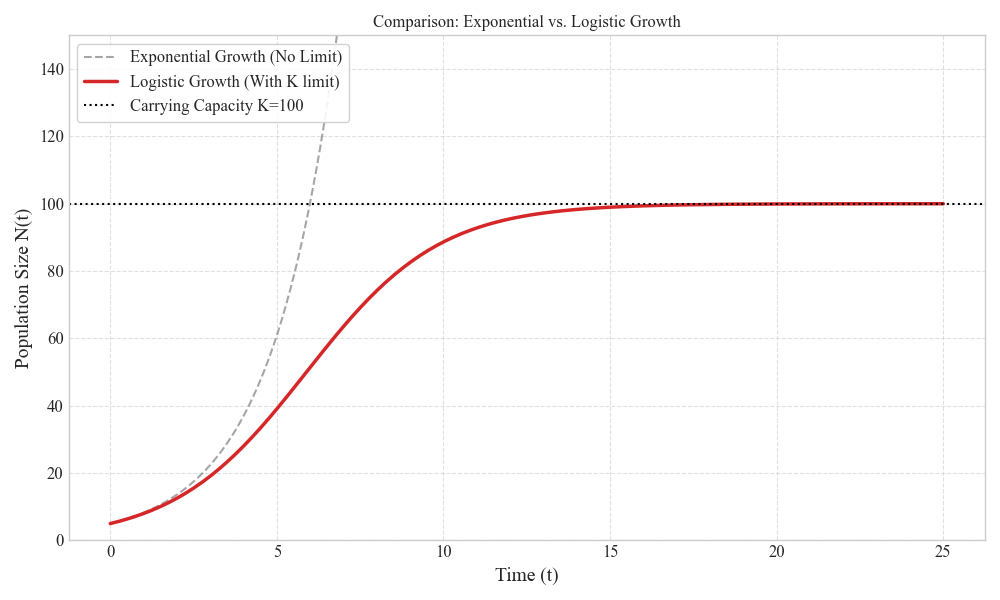
关于生长曲线，不妨模拟一个种群从极少数量（N0）开始的生长过程。为了直观对比，设定相同的初始增长率（r），唯一的区别在于是否引入环境容量限制。在指数模型中，设定环境资源无限，种群仅受自身繁殖能力的驱动，呈现"J型"爆发式增长；而在Logistic模型中，我们设定了一个固定的环境天花板（K），该参数模拟了有限的空间或食物。随着种群数量接近KK值，增长速度被数学项 (1−N/K) 逐渐"刹车"直至归零，从而迫使曲线呈现出经典的"S型"稳定状态。

完整代码如下：

python 复制代码

import matplotlib
matplotlib.use('TkAgg') 
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# 设置绘图风格
plt.style.use('seaborn-v0_8-whitegrid')
plt.rcParams['font.family'] = 'serif'
plt.rcParams['font.serif'] = ['Times New Roman'] + plt.rcParams['font.serif']
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
plt.rcParams['legend.fontsize'] = 12

# --- 模型定义 ---
def growth_models(N, t, r, K, model_type='logistic'):
    """
    N: 种群数量
    t: 时间
    r: 增长率
    K: 环境容量
    model_type: 'exponential' 或 'logistic'
    """
    if model_type == 'exponential':
        # 指数增长: dN/dt = rN
        dNdt = r * N
    else:
        # Logistic增长: dN/dt = rN(1 - N/K)
        dNdt = r * N * (1 - N / K)
    return dNdt

# --- 参数设定 ---
r = 0.5       # 增长率
K = 100       # 环境容量 K
N0 = 5        # 初始种群数量
t = np.linspace(0, 25, 200) # 时间范围 0-25

# --- 求解方程 ---
# 1. 解指数增长
N_exp = odeint(growth_models, N0, t, args=(r, K, 'exponential'))
# 2. 解Logistic增长
N_log = odeint(growth_models, N0, t, args=(r, K, 'logistic'))

# --- 绘图 ---
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制指数增长（截断一下y轴以免图形被拉得太长）
ax.plot(t, N_exp, label='Exponential Growth (No Limit)', linestyle='--', color='gray', alpha=0.7)

# 绘制Logistic增长
ax.plot(t, N_log, label='Logistic Growth (With K limit)', color='#d62728', linewidth=2.5)

# 绘制环境容量K的辅助线
ax.axhline(y=K, color='black', linestyle=':', label=f'Carrying Capacity K={K}')

# 图表装饰
ax.set_ylim(0, 150) # 限制Y轴便于观察Logistic曲线的S型
ax.set_xlabel('Time (t)')
ax.set_ylabel('Population Size N(t)')
ax.set_title('Comparison: Exponential vs. Logistic Growth')
ax.legend(loc='upper left', frameon=True, framealpha=0.9)
ax.grid(True, linestyle='--', alpha=0.6)

plt.tight_layout()
plt.show()

运行结果如下：

二、Lotka-Volterra方程

这一部分的设定不再关注单一物种，而是建立了两个微分方程组来描述两个物种（N1,N2）之间的动态耦合关系。

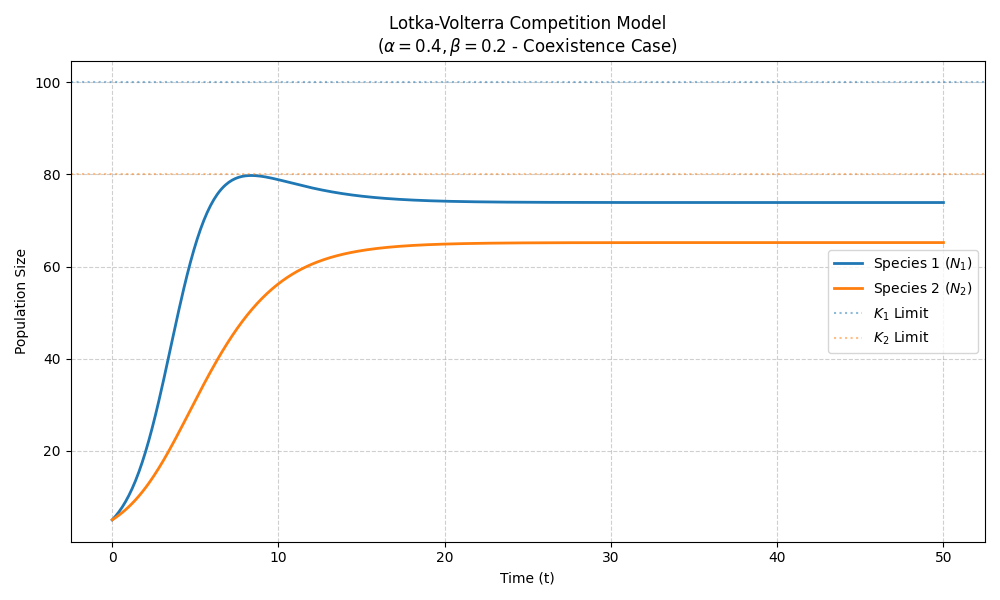
在竞争模型中，设定两个物种共享有限资源，引入了竞争系数（α,β）来量化一方对另一方的生存压力。参数被特意设定为"弱竞争"区间，使得两个物种虽然相互抑制，但最终能分别占据一部分生态位而实现共存，而不是发生竞争排斥导致一方灭绝。
在捕食模型中，我们将关系设定为非对称的能量流动：猎物的减少直接转化为捕食者的增加。我们设定了特定的捕食效率和转化率，模拟出了一种"时间滞后"效应------即捕食者数量的峰值总是滞后于猎物数量的峰值，从而在数学上形成了永不停止的相位差振荡周期。

完整代码如下：

python 复制代码

import matplotlib
matplotlib.use('TkAgg') 
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint


# --- 模型定义 ---
def competition_model(N, t, r1, r2, K1, K2, alpha, beta):
    """
    N: 包含 [N1, N2] 的数组
    alpha: 物种2对物种1的竞争系数
    beta: 物种1对物种2的竞争系数
    """
    N1, N2 = N

    # 竞争方程
    dN1dt = r1 * N1 * (1 - (N1 + alpha * N2) / K1)
    dN2dt = r2 * N2 * (1 - (N2 + beta * N1) / K2)

    return [dN1dt, dN2dt]


# --- 参数设定 ---
# 这种参数组合下，种群内部竞争 > 种群间竞争，通常能共存
r1 = 0.8;
r2 = 0.5  # 增长率
K1 = 100;
K2 = 80  # 各自环境容量
alpha = 0.4  # N2 对 N1 的影响较小
beta = 0.2  # N1 对 N2 的影响较小
N0 = [5, 5]  # 初始数量都很少

t = np.linspace(0, 50, 500)

# --- 求解 ---
solution = odeint(competition_model, N0, t, args=(r1, r2, K1, K2, alpha, beta))
N1_sol = solution[:, 0]
N2_sol = solution[:, 1]

# --- 绘图 ---
fig, ax = plt.subplots(figsize=(10, 6))

ax.plot(t, N1_sol, label=r'Species 1 ($N_1$)', color='#1f77b4', linewidth=2)
ax.plot(t, N2_sol, label=r'Species 2 ($N_2$)', color='#ff7f0e', linewidth=2)

# 绘制各自的K值辅助线
ax.axhline(K1, color='#1f77b4', linestyle=':', alpha=0.5, label=r'$K_1$ Limit')
ax.axhline(K2, color='#ff7f0e', linestyle=':', alpha=0.5, label=r'$K_2$ Limit')

ax.set_xlabel('Time (t)')
ax.set_ylabel('Population Size')
ax.set_title(f'Lotka-Volterra Competition Model\n($\\alpha={alpha}, \\beta={beta}$ - Coexistence Case)')
ax.legend(loc='center right', frameon=True)
ax.grid(True, linestyle='--', alpha=0.6)

plt.tight_layout()
plt.show()

运行结果：

三、Monod方程

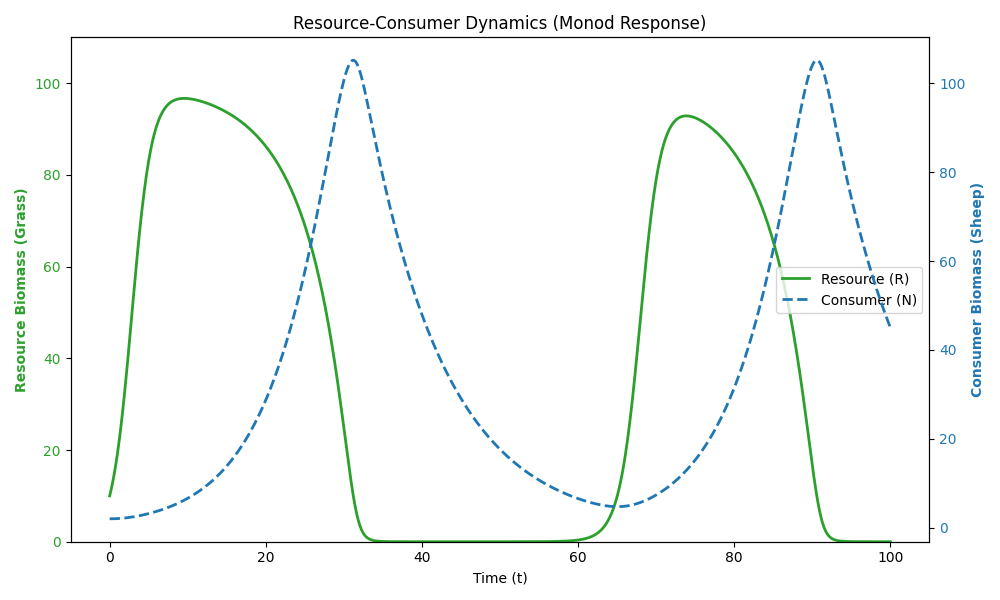
这段设定的核心在于打破了"资源是固定常数K"的假设，按照第一篇原理讲解时的比喻，将草（资源R）和羊（消费者N）都视为随时间变化的动态变量。我们设定草自身遵循Logistic恢复规律，但会被羊消耗；而羊的摄食行为不再是简单的线性关系，而是引入了机制：设定了半饱和常数（Ks）和最大摄食速率（Vmax）。这意味着，即使草极度丰富，羊的进食速度也有生理极限（即吃饱了），不会无限增加。这种设定更符合真实的生物学机制，模拟了消费者数量如何严格受限于资源的再生速度和自身的消化能力，最终两者在动态中达到某种生态平衡。

完整代码如下：

python 复制代码

import matplotlib
matplotlib.use('TkAgg')  
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint


# --- 模型定义 ---
def resource_consumer(state, t, r_grass, Kg, Vmax, Ks, e, d):
    """
    state: [Resource(Grass), Consumer(Sheep)]
    r_grass: 草的恢复速率
    Kg: 草的环境容量
    Vmax: 羊的最大摄食速率
    Ks: 半饱和常数 (Monod方程参数)
    e: 能量转化效率 (草 -> 羊)
    d: 羊的死亡率
    """
    R, N = state

    # 摄食函数 (Monod / Michaelis-Menten)
    # 羊吃草的速率，取决于草有多少
    uptake_rate = Vmax * (R / (Ks + R))

    # 1. 草的方程: Logistic生长 - 被羊吃掉的总量
    # 假设每单位羊吃掉 uptake_rate 的草
    dRdt = r_grass * R * (1 - R / Kg) - uptake_rate * N

    # 2. 羊的方程: 转化效率 * 吃的草 - 死亡
    dNdt = e * uptake_rate * N - d * N

    return [dRdt, dNdt]


# --- 参数设定 ---
r_grass = 0.8  # 草长得比较快
Kg = 100.0  # 草最多能长到100单位
Vmax = 0.5  # 羊吃得很快
Ks = 20.0  # 草少于20时，羊进食变难
e = 0.6  # 转化率：吃100斤草长60斤肉（假设）
d = 0.1  # 羊的死亡率

# 初始状态
state0 = [10, 2]  # 草很少(10)，羊也很少(2)
t = np.linspace(0, 100, 1000)

# --- 求解 ---
sol = odeint(resource_consumer, state0, t, args=(r_grass, Kg, Vmax, Ks, e, d))
R_sol = sol[:, 0]  # 草
N_sol = sol[:, 1]  # 羊

# --- 绘图 (双Y轴) ---
fig, ax1 = plt.subplots(figsize=(10, 6))

color = 'tab:green'
ax1.set_xlabel('Time (t)')
ax1.set_ylabel('Resource Biomass (Grass)', color=color, fontweight='bold')
ax1.plot(t, R_sol, color=color, linewidth=2, label='Resource (R)')
ax1.tick_params(axis='y', labelcolor=color)
ax1.set_ylim(0, Kg * 1.1)

# 实例化共享x轴的第二个y轴
ax2 = ax1.twinx()
color = 'tab:blue'
ax2.set_ylabel('Consumer Biomass (Sheep)', color=color, fontweight='bold')
ax2.plot(t, N_sol, color=color, linewidth=2, linestyle='--', label='Consumer (N)')
ax2.tick_params(axis='y', labelcolor=color)

# 添加标题和图例
plt.title('Resource-Consumer Dynamics (Monod Response)')
# 手动添加图例以合并两个轴
lines_1, labels_1 = ax1.get_legend_handles_labels()
lines_2, labels_2 = ax2.get_legend_handles_labels()
ax1.legend(lines_1 + lines_2, labels_1 + labels_2, loc='center right')

plt.tight_layout()
plt.show()