练题100天——DAY34：错误的集合+图片平滑器+最长连续递增序列

今天记录了3道题，难度范围：★~★★，因为后面两道都可以通过暴力法解答，并且官方也是使用的暴力法，所以难度为★。

一.错误的集合 ★★☆☆☆

题目

645. 错误的集合 集合 s 包含从 1 到 n 的整数。不幸的是，因为数据错误，导致集合里面某一个数字复制成了集合里面的另外一个数字的值，导致集合 丢失了一个数字 并且 有一个数字重复 。

给定一个数组 nums 代表了该集合发生错误后的结果。

请你找出重复出现的整数，再找到丢失的整数，将它们以数组的形式返回。

思路1------哈希表

遍历数组，利用哈希表存储数组的元素值及其出现次数，出现次数为2的元素就是重复出现的数，将其存入结果数组res。

遍历1~n，在哈希表中找1~n，没有找到的数就是丢失的数，将其存入结果数组res，然后可以直接退出循环。

代码

class Solution {
public:
    vector<int> findErrorNums(vector<int>& nums) {
        int n=nums.size();
        unordered_map<int,int> map;
        vector<int> res;
        for(int i=0;i<n;i++){
            map[nums[i]]++;
            //重复的整数
            if(map[nums[i]]==2){
                res.push_back(nums[i]);
            }
        }
        for(int i=1;i<=n;i++){
            //丢失的整数
            if(map.count(i)==0){
                res.push_back(i);
                break;
            }
        }
        return res;
    }
};

复杂度

N为数组nums的长度

时间复杂度：O(N)。遍历次数N+N，所以整体的时间复杂度为O(N)

空间复杂度：O(N)。哈希表的空间复杂度为O(N-1)，其他常量级变量的空间复杂度为O(1)，所以整体的空间复杂度为O(N-1)+O(1)=O(N)

思路2------排序

先将数组nums进行升序排列操作，使得重复的数相邻，且缺少数的地方的两个数相差2。

先找重复数：前后相等的数就是重复数，将其放入数组res。

再找缺失数：需要将缺失数分为三种情况，因为缺少数的地方的两个数相差2，需要前后两个数相减，在数组首尾无法获取两个数，所以需要单独处理。将情况分为：缺失数为1、缺失数在中间以及缺失数为n三种情况，进行不同的处理。将缺失的数放入res后即可返回。

代码

class Solution {
public:
    vector<int> findErrorNums(vector<int>& nums) {
        int n = nums.size();
        vector<int> res(2);
        sort(nums.begin(), nums.end());
        // 先找重复数
        for (int i = 0; i < n - 1; ++i) {
            if (nums[i] == nums[i + 1]) {
                res[0] = nums[i];
                break;
            }
        }
        // 再找缺失数
        // 情况1：缺失数是1
        if (nums[0] != 1) {
            res[1] = 1;
            return res;
        }
        // 情况2：缺失数在中间
        for (int i = 0; i < n - 1; ++i) {
            if (nums[i + 1] - nums[i] > 1) {
                res[1] = nums[i] + 1;
                return res;
            }
        }
        // 情况3：缺失数是n
        res[1] = n;

        return res;
    }
};

复杂度

N为数组nums的长度

时间复杂度：O(NlogN)。排序算法时间O(NlogN)，遍历时间O(N-1+N-1)=O(N)，所以整体的时间复杂度为O(NlogN)+O(N)=O(NlogN)。

空间复杂度：O(logN)。排序算法所需的栈空间O(logN)，其他变量O(1)，所以整体的空间复杂度为O(logN)+O(1)=O(logN)。

优化

官方利用排序的代码。复杂度没有变化，但是思路太一样。

思路：为了寻找丢失的数字，需要在遍历已排序数组的同时记录上一个元素，然后计算当前元素与上一个元素的差。考虑到丢失的数字可能是 1，因此需要将上一个元素初始化为 0。

当丢失的数字小于 n 时，通过计算当前元素与上一个元素的差，即可得到丢失的数字；如果 nums[n−1]不等于n，则丢失的数字是 n

class Solution {
public:
    vector<int> findErrorNums(vector<int>& nums) {
        int n = nums.size();
        vector<int> res(2);
        sort(nums.begin(), nums.end());
        int prev=0;
        for(int i=0;i<n;i++){
            int cur=nums[i];
            if(prev==cur){
                res[0]=cur;
            }else if(cur-prev>1){
                res[1]=prev+1;
            }
            prev=cur;
        }
        if(nums[n-1]!=n){
            res[1]=n;
        }
        return res;
    }
};

复杂度

N为数组nums的长度

时间复杂度：O(NlogN)。排序算法时间O(NlogN)，遍历时间O(N)，所以整体的时间复杂度为O(NlogN)+O(N)=O(NlogN)。

空间复杂度：O(logN)。排序算法所需的栈空间O(logN)，其他变量O(1)，所以整体的空间复杂度为O(logN)+O(1)=O(logN)。

官方题解------位运算 ★★★★☆

1.若将数组中所有数 与1~n 的所有数 进行异或，最终结果为 重复数^缺失数，令结果为xor，因为数组中除了 "重复数出现两次"、"缺失数出现 0 次"，其余数都出现一次；1~n 的数都出现一次。异或后，其余数相互抵消（a⊕a=0）

2.令lowbit=xor&(-xor)，则lowbit为重复数 x 和缺失数 y 的二进制表示中的最低不同位 。xor=x^y的二进制中，所有为 1 的位，都表示x和y在该位上的值不同；lowbit取的是xor中最右边的 1 ，也就是x和y的二进制最低不同位 （记为第k位）

3.将2n个数字分为两组，第一组的每个数字a都满足a&lowbit=0，第二组的每个数字都满足b&lowbit != 0，即

• 第一组：a & lowbit == 0 → 数字a的第k位是 0；
• 第二组：b & lowbit != 0 → 数字b的第k位是 1。
• x和y最后必然出现在不同的组里

4.创建变量num1和num2，初始为0，再次遍历2n个数字，对于每个数字a，若a&lowbit=0，则令num1=num1⊕a，反之，令num2=num2⊕a，这样一来就将3中的两组数组异或到不同的变量中。同一数字只可能出现在同一组，所以最后num1和num2的值就是重复数和缺失数，但是不确定谁和谁对应。

5.再次遍历nums，如果nums中存在num1，则num1是重复数，num2是缺失数；反之，num2是重复数，num1是缺失数.

代码

class Solution {
public:
    vector<int> findErrorNums(vector<int>& nums) {
        int n = nums.size();
        int xorSum=0;//2n个数异或结果
        for(int num:nums){
            xorSum^=num;
        }
        for(int i=1;i<=n;i++){
            xorSum^=i;
        }
        //重复数和缺失数二进制表示下最低不同位
        int lowbit=xorSum&(-xorSum);
        //分组异或
        int num1=0,num2=0;
        for(int &num:nums){
            if((num&lowbit)==0){
                num1^=num;
            }else{
                num2^=num;
            }
        }
        for(int i=1;i<=n;i++){
            if((i&lowbit)==0){
                num1^=i;
            }else{
                num2^=i;
            }
        }
        for(int num:nums){
            //num存在于num1中，为重复数
            if(num==num1){
                return vector<int>{num1,num2};
            }
        }
        //num1不存在于num1中，为缺失数
        return vector<int>{num2,num1};
    }
};

复杂度

N为数组nums的长度

时间复杂度：O(N)。整个过程需要对数组 nums 遍历 3 次，以及遍历从 1 到 n 的每个数 2 次。

空间复杂度：O(1)。只需要常数的额外空间。

二.图片平滑器 ★☆☆☆☆

题目

661. 图片平滑器 图像平滑器 是大小为 3 x 3 的过滤器，用于对图像的每个单元格平滑处理，平滑处理后单元格的值为该单元格的平均灰度。

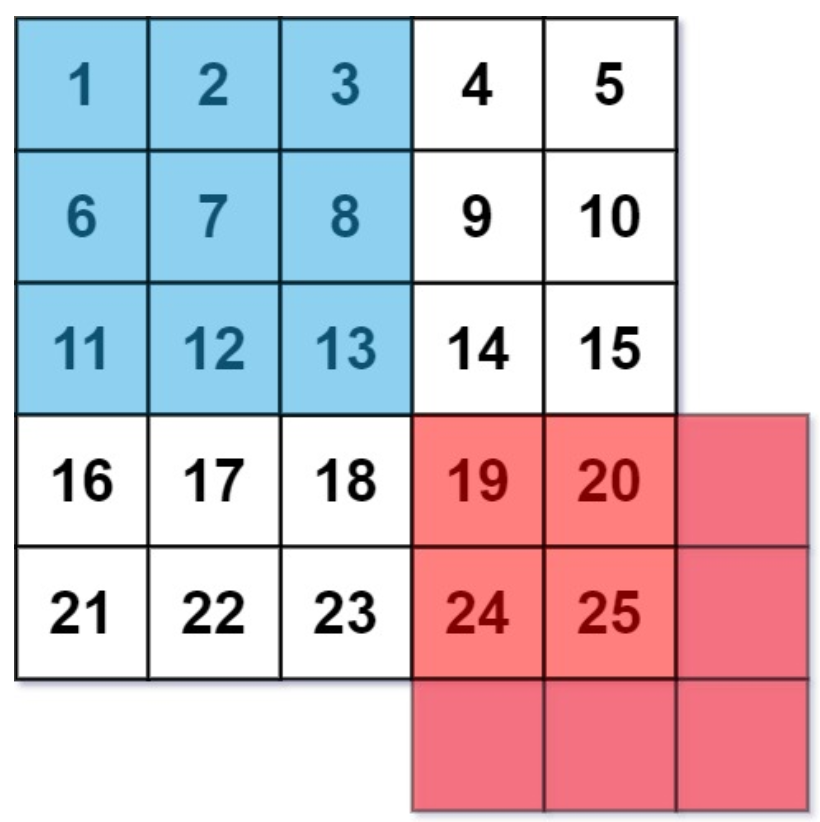
每个单元格的平均灰度 定义为：该单元格自身及其周围的 8 个单元格的平均值，结果需向下取整。（即，需要计算蓝色平滑器中 9 个单元格的平均值）。

如果一个单元格周围存在单元格缺失的情况，则计算平均灰度时不考虑缺失的单元格（即，需要计算红色平滑器中 4 个单元格的平均值）。

思路

遍历img中的每一个点，求出该点与周围的点的数值总和sum，以及点的个数count，给结果数组res的对应位置赋值为sum/count。

代码

利用多个 if 语句对周围的点进行合理性判断，再加到sum中

class Solution {
public:
    vector<vector<int>> imageSmoother(vector<vector<int>>& img) {
        int rowLen = img.size();
        int colLen = img[0].size();
        // 关键修复1：初始化结果数组，分配和输入相同的行列大小
        vector<vector<int>> res(rowLen, vector<int>(colLen, 0));

        for (int i = 0; i < rowLen; i++) {
            for (int j = 0; j < colLen; j++) {
                int sum = 0;
                int count = 0;
                // 第一行：i-1行（上一行）
                if (i - 1 >= 0) {
                    if (j - 1 >= 0) { // 左上
                        sum += img[i - 1][j - 1];
                        count++;
                    }
                    // 正上
                    sum += img[i - 1][j];
                    count++;
                    if (j + 1 < colLen) { // 右上
                        sum += img[i - 1][j + 1];
                        count++;
                    }
                }
                // 第二行：i行（当前行）
                if (j - 1 >= 0) { // 左
                    sum += img[i][j - 1];
                    count++;
                }
                // 当前
                sum += img[i][j];
                count++;
                if (j + 1 < colLen) { // 右
                    sum += img[i][j + 1];
                    count++;
                }
                // 第三行：i+1行（下一行）
                if (i + 1 < rowLen) {
                    if (j - 1 >= 0) { // 左下
                        sum += img[i + 1][j - 1];
                        count++;
                    }
                    // 正下
                    sum += img[i + 1][j];
                    count++;
                    if (j + 1 < colLen) { // 右下
                        sum += img[i + 1][j + 1];
                        count++;
                    }
                }
                // 计算平均值并赋值给结果数组
                res[i][j] = sum / count;
            }
        }
        return res;
    }
};

优化

通过遍历 3x3 偏移量简化代码，利用dx、dy表示偏移量，x和y表示偏移后的点的坐标，只有在x、y都合法的时候，才能加入sum

class Solution {
public:
    vector<vector<int>> imageSmoother(vector<vector<int>>& img) {
        int rowLen = img.size();
        int colLen = img[0].size();
        vector<vector<int>> res(rowLen, vector<int>(colLen, 0));
        int sum = 0;
        for (int i = 0; i < rowLen; i++) {
            for (int j = 0; j < colLen; j++) {
                int sum = 0;
                int count = 0;
                for (int dx = -1; dx <= 1; dx++) {
                    for (int dy = -1; dy <= 1; dy++) {
                        int x = i + dx;
                        int y = j + dy;
                        if (x >= 0 && x < rowLen && y >= 0 && y < colLen) {
                            sum += img[x][y];
                            count++;
                        }
                    }
                }
                res[i][j] = sum / count;
            }
        }
        return res;
    }
};

复杂度

N为数组img的元素的个数

时间复杂度：O(N)。循环遍历N个元素的时间复杂度为O(N)，如果加上偏移循环的时间复杂度O(9)，整体的时间复杂度仍为O(N)

空间复杂度：O(1)。只需要常数的额外空间，结果数组res的空间不算入。

PS：过滤器的宽高C 是常数时，渐进复杂度不计入；精确分析时可计入，但算法分析中默认用渐进复杂度，因此答案是 O (N)，C 不算

三.最长连续递增序列 ★☆☆☆☆

题目

674. 最长连续递增序列

给定一个未经排序的整数数组，找到最长且连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

思路1------暴力法

遍历数组，遍历到每一个元素nums[ i ]时，再遍历x之后的每个元素nums[ j ]，nums[ j ]不仅要>nums[ i ]，还要大于nums[ i ]和nums[ j ]之间的元素，要呈现递增的趋势。

代码

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int n=nums.size();
        //暴力法
        int res=0;
        for(int i=0;i<n;i++){
            int count=1;
            for(int j=i+1;j<n;j++){
                if(nums[j]<=nums[i] || nums[j]<=nums[j-1]){
                    break;
                }
                count++;
            }
            res=max(res,count);
        }
        return res;
    }
};

复杂度

N为数组nums的长度

时间复杂度：O(N²)。最坏情况的遍历次数：N+N-1+N-2+N-3+...+1=N*(N+1)/2

因此时间复杂度应为 O(N²)。

空间复杂度：O(1)。

思路2------双指针

用 i 表示子序列的起始索引，比较nums[ j ]和nums[ j-1 ]并不断移动 j，只要后一个数比前一个数就是递增的序列，并且在nums[ j ]>nums[ j-1 ]时一直更新res，使其保存最长连续递增序列的长度。当nums[ j ]<=nums[ j-1 ]时，重新计算连续递增序列，将当前的 j 作为起始点赋值给 i，然后再移动 j。遍历完整个数组后，res的值就是最长连续递增序列的长度。

代码

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) {
            return 1;
        }
        int res = 1;
        int i = 0;
        int j = 1;
        while (j < n) {
            if(nums[j]>nums[j-1]){
                j++;
                res=max(res,j-i);
            }
            else{
                i=j;
                j++;
            }
        }
        return res;
    }
};

复杂度

N为数组nums的长度

时间复杂度：O(N)。遍历N次。

空间复杂度：O(1)。