《人工智能基础》[算法篇5]：SVM算法解析

一、SVM 是什么？

在日常生活中，我们常常需要对事物进行分类。比如整理衣物时，会将上衣、裤子、袜子等分别归类放置；整理书籍时，会按照文学、科学、历史等类别将书籍摆放整齐。在机器学习领域，也有类似的任务，支持向量机（Support Vector Machine，SVM）就是一种强大的分类工具 。

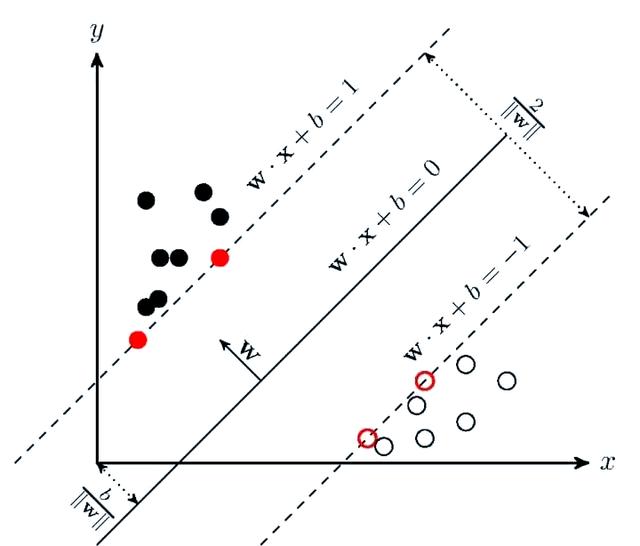
SVM的全称是"Support Vector Machine"，即支持向量机。它是一种在机器学习中广泛使用的监督学习模型，主要用于分类和回归任务（SVR）。SVM通过寻找一个超平面（在二维空间中是一条直线，在三维空间中是一个平面，在更高维的空间中SVM 寻找的是一个超平面）来对数据进行分类，使得不同类别的数据被这个超平面分隔开来，并且尽可能地远离彼此。

假设我们有一堆水果，包括苹果和橙子，我们可以把它们的特征（比如颜色、大小、形状等）看作是数据的维度。SVM 的目标就是找到一个合适的 "边界"，根据这些特征将苹果和橙子准确地分开。这个边界就是决策边界，而 SVM 的独特之处在于，它寻找的是能够使两类数据之间的间隔最大化的决策边界。

二、SVM 的工作原理

2.1、工作原理

2.1.1、算力原理

在了解 SVM 的工作原理之前，我们先明确一个概念：线性可分。简单来说，如果在一个数据集中，我们可以找到一个超平面（在二维空间中是一条直线，三维空间中是一个平面，更高维空间中是超平面），将不同类别的数据点完全分开，那么这个数据集就是线性可分的。

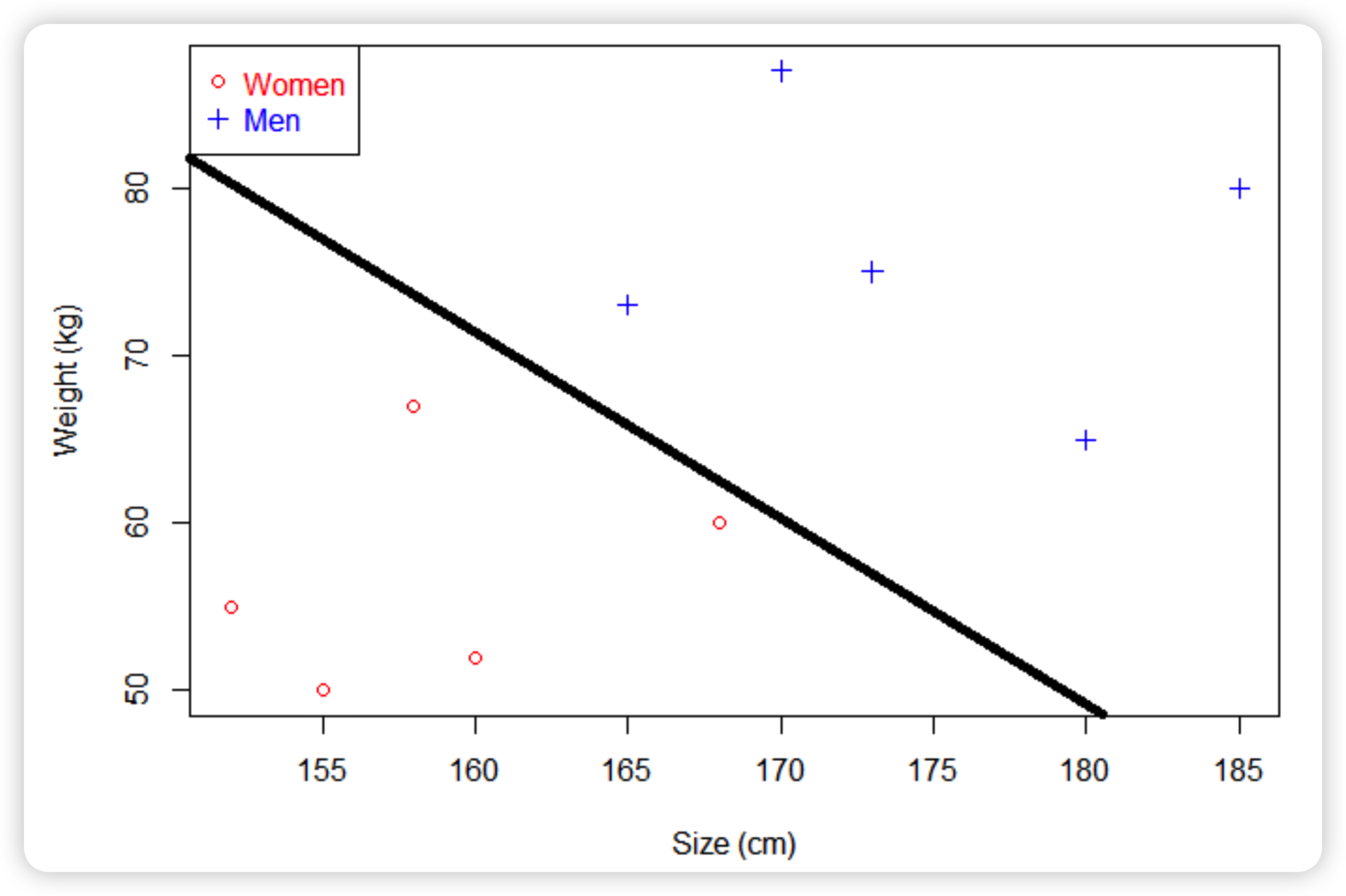
现在有一些人的身高和体重数据，将它们绘制成散点图

如果现在给你一个未知男女的身高和体重，你能分辨出性别吗？直接将已知的点划分为两部分，这个点落在哪一部分就对应相应的性别。那就可以画一条直线，直线以上是男生，直线以下是女生。（男生身高、体重一般比女生数值大）

超平面是平面的一般化

• 在一维的平面中，它是点

• 在二维的平面中，它是线

• 在三维的平面中，它是面

• 在更高的维度中，称之为超平面

相关概念：

• ‌超平面‌，是SVM中用于分割数据的决策边界

• ‌支持向量，‌是离最优超平面最近的训练样本点，这些点直接决定了超平面的位置和方向

2.1.2、数学原理

线性可分性（linear separability）：

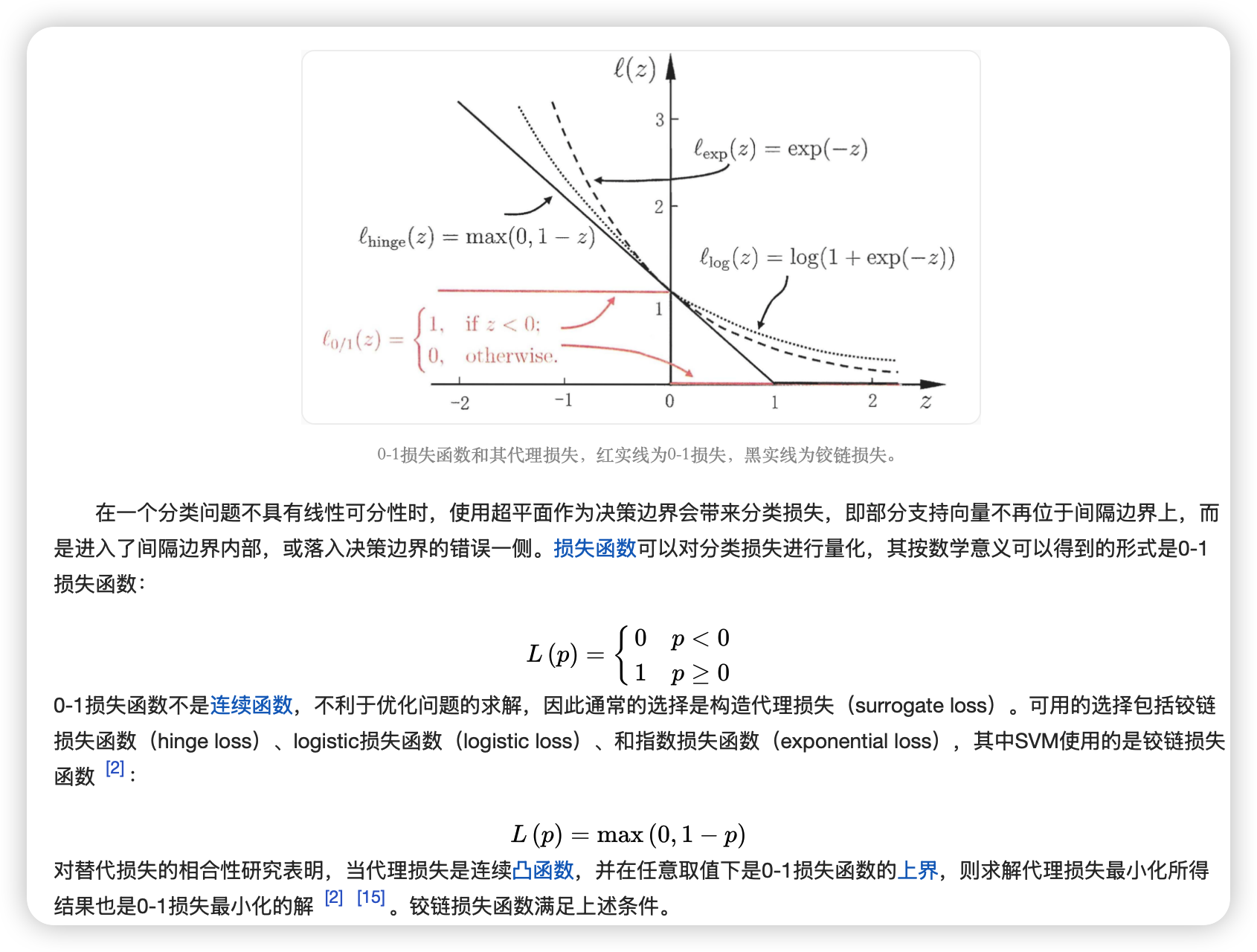
损失函数：

核方法：

核函数：

在构造核函数后，验证其对输入空间内的任意格拉姆矩阵为半正定矩阵是困难的，因此通常的选择是使用现成的核函数 。以下给出一些核函数的例子：

当多项式核的阶为1时，其被称为线性核，对应的非线性分类器退化为线性分类器。RBF核也被称为高斯核（Gaussian kernel），其对应的映射函数将样本空间映射至无限维空间。

2.2、线性SVM与非线性SVM

SVM最初是为解决线性分类问题而设计的，然而现实世界中的数据往往不是线性可分的。为了处理非线性数据，SVM引入了核函数的概念。

线性SVM：适用于线性可分的数据集。通过求解一个二次规划问题，找到最优超平面的权重向量和偏置项，从而实现对数据的分类。

非线性SVM：通过核函数将输入数据映射到高维特征空间，使得原本在原始空间中线性不可分的数据变得线性可分。常用的核函数包括多项式核、径向基函数（RBF）核等。

2.3、使用技巧

核函数是SVM中实现非线性分类的关键，选择合适的核函数和参数非常重要。通过交叉验证等方法，可以评估不同核函数和参数组合的性能，从而选择最优的核函数和参数。

常用核函数：

• 线性核：适用于线性可分的数据集

• 多项式核：通过增加多项式特征，提升数据维度，适用于处理低维非线性数据

• RBF核（高斯核）：将样本投射到无限维空间，适用于处理高维非线性数据

参数优化：

• C参数：惩罚系数，控制分类间隔和分类错误之间的权衡。C值越大，分类间隔越小，分类错误越少，但可能导致过拟合

• γ参数（对于RBF核）：决定数据的映射范围和复杂度。γ值越大，映射范围越小，模型复杂度越高，可能导致过拟合

  损失函数和最优化：SVM 通过最小化损失函数和引入正则化项来求解最优的超平面，以得到最佳的分类结果

三、SVM 算法实战

下面通过 Python 代码示例，更直观地了解 SVM 在实际中的应用，我们将使用 Python 的 scikit - learn 库来实现 SVM。这个库提供了丰富的机器学习算法和工具，能帮助我们快速实现 SVM 模型开发。

3.1、完成代码示例

 import numpy as np
 import matplotlib.pyplot as plt
 from sklearn import datasets
 from sklearn.svm import SVC
 from sklearn.model_selection import train_test_split
 from sklearn.metrics import accuracy_score, classification_report
 ​
 # 加载鸢尾花数据集
 iris = datasets.load_iris()
 X = iris.data[:, :2]  # 只取前两个特征方便可视化
 y = iris.target
 ​
 # 划分训练集和测试集
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
 ​
 # 创建SVM分类器（使用RBF核）
 svm_model = SVC(kernel='rbf', gamma='scale')
 ​
 # 训练模型
 svm_model.fit(X_train, y_train)
 ​
 # 预测测试集
 y_pred = svm_model.predict(X_test)
 ​
 # 输出准确率和分类报告
 print("Accuracy:", accuracy_score(y_test, y_pred))
 print("\nClassification Report:\n", classification_report(y_test, y_pred))
 ​
 # 可视化决策边界
 def plot_decision_boundary(X, y, model, title):
     h = .02  # 步长
     x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
     y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
     xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                          np.arange(y_min, y_max, h))
     
     Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
     Z = Z.reshape(xx.shape)
     
     plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.coolwarm)
     scatter = plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, edgecolors='k')
     plt.title(title)
     plt.xlabel('Feature 1')
     plt.ylabel('Feature 2')
     plt.colorbar(scatter)
     plt.show()
 ​
 # 绘制决策边界
 plot_decision_boundary(X_train, y_train, svm_model, "SVM Decision Boundary (Training Set)")

运行结果：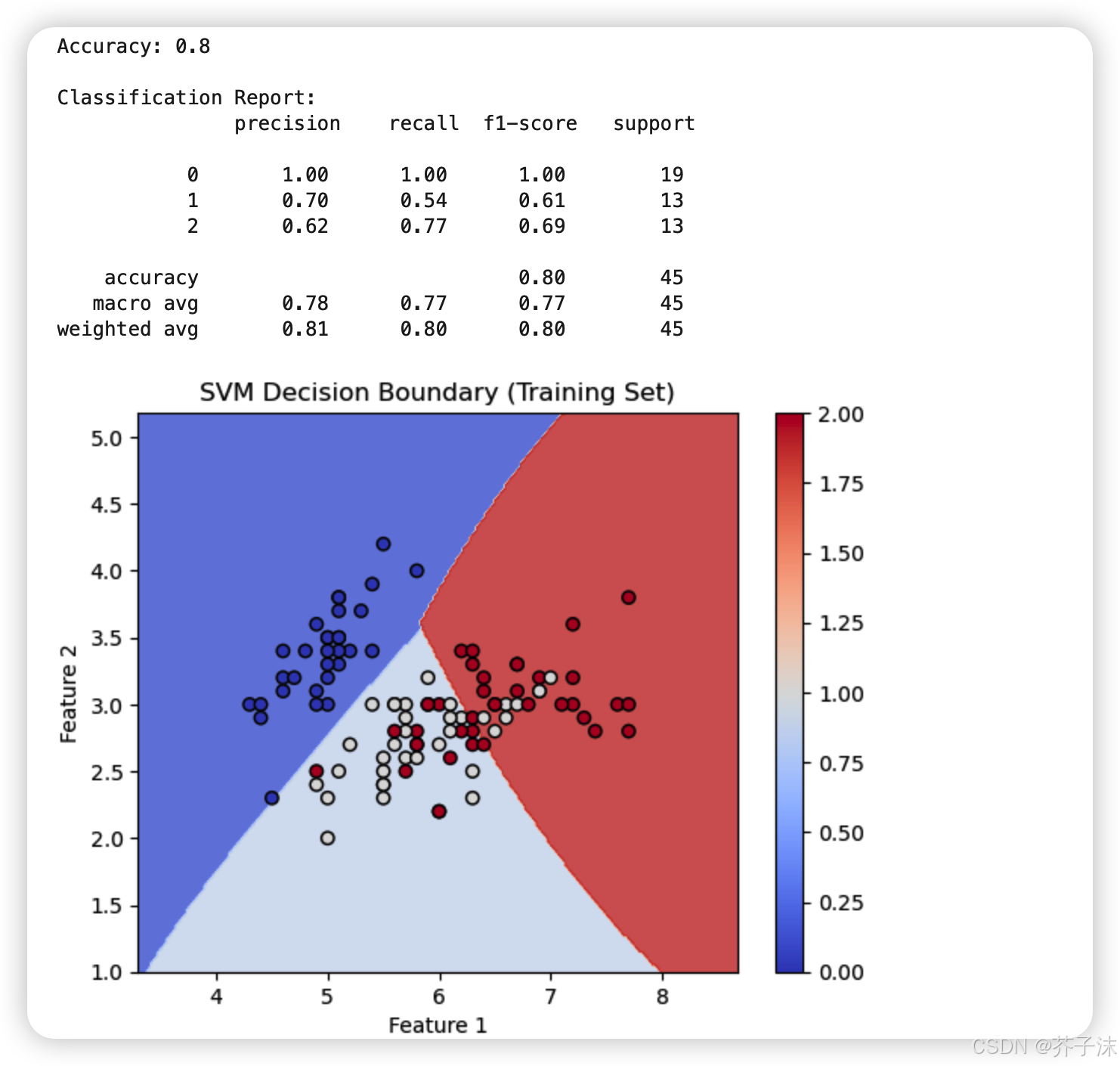

3.1、准备工作

首先，导入所需的库，包括用于数据处理的numpy，用于数据可视化的matplotlib.pyplot，用于加载数据集的datasets，用于划分数据集的train_test_split，用于实现 SVM 的SVC，以及用于评估模型的classification_report和confusion_matrix。

 import numpy as np
 import matplotlib.pyplot as plt
 from sklearn import datasets
 from sklearn.model_selection import train_test_split
 from sklearn.svm import SVC
 from sklearn.metrics import classification_report, confusion_matrix

3.2、数据集准备

这里我们以鸢尾花数据集为例，它是一个经典的多分类数据集，包含了 150 个样本，每个样本有 4 个特征，分别是花萼长度、花萼宽度、花瓣长度和花瓣宽度，共分为 3 个类别。为了便于可视化，我们只选取前两个特征。然后，使用train_test_split函数将数据集划分为训练集和测试集，其中测试集占比 30%，并设置随机种子random_state为 42，以确保结果的可重复性。

 # 加载鸢尾花数据集
 iris = datasets.load_iris()
 # 只取前两个特征
 X = iris.data[:, :2]
 y = iris.target
 # 划分训练集和测试集
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

3.3、模型创建与训练

接下来，创建 SVM 模型并进行训练。我们分别创建使用线性核和高斯核的 SVM 模型。在创建模型时，设置kernel='linear'表示使用线性核，kernel='rbf'表示使用高斯核，C是惩罚参数，用于控制模型对错误分类的惩罚程度。这里将C设置为 1.0，gamma是高斯核的系数，设置为'scale'表示根据数据自动调整。然后，使用训练集数据对模型进行训练。

 # 创建线性核SVM模型
 clf_linear = SVC(kernel='linear', C=1.0)
 clf_linear.fit(X_train, y_train)
 ​
 # 创建高斯核SVM模型
 # 创建SVM分类器（使用RBF核）
 svm_model = SVC(kernel='rbf', C=1.0, gamma='scale')
 # 训练模型
 svm_model.fit(X_train, y_train)

3.4、模型预测与评估

模型训练完成后，使用测试集数据进行预测，并评估模型的性能。使用predict方法对测试集进行预测，得到预测结果y_pred。然后，使用confusion_matrix函数计算混淆矩阵，它可以直观地展示模型在各个类别上的分类情况，比如有多少样本被正确分类，有多少样本被误分类。再使用classification_report函数生成分类报告，其中包含精确率、召回率、F1 值等评估指标，这些指标可以更全面地评估模型的性能。

 # 线性核SVM模型预测
 y_pred_linear = clf_linear.predict(X_test)
 # 高斯核SVM模型预测
 y_pred_rbf = clf_rbf.predict(X_test)
 # 线性核SVM模型评估
 print("线性核SVM模型混淆矩阵：")
 print(confusion_matrix(y_test, y_pred_linear))
 print("线性核SVM模型分类报告：")
 print(classification_report(y_test, y_pred_linear))
 # 高斯核SVM模型评估
 print("高斯核SVM模型混淆矩阵：")
 print(confusion_matrix(y_test, y_pred_rbf))
 print("高斯核SVM模型分类报告：")
 print(classification_report(y_test, y_pred_rbf))

3.5、决策边界可视化

为了更直观地理解 SVM 模型的分类效果，我们绘制决策边界。定义一个函数plot_decision_boundary，它接受模型、数据特征和标签作为参数。在函数内部，首先获取数据特征的最小值和最大值，然后使用np.meshgrid函数创建一个网格，这个网格覆盖了数据特征的取值范围。接着，使用模型对网格中的每个点进行预测，得到预测结果Z。最后，使用plt.contourf函数绘制决策边界，它会根据预测结果Z填充不同的颜色，以表示不同的类别。再使用plt.scatter函数绘制数据点，其中颜色根据标签y来确定，这样我们就可以直观地看到模型的决策边界和数据点的分布情况。

 # 可视化决策边界
 def plot_decision_boundary(X, y, model, title):
     h = .02  # 步长
     x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
     y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
     xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                          np.arange(y_min, y_max, h))
     
     Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
     Z = Z.reshape(xx.shape)
     
     plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.coolwarm)
     scatter = plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, edgecolors='k')
     plt.title(title)
     plt.xlabel('Feature 1')
     plt.ylabel('Feature 2')
     plt.colorbar(scatter)
     plt.show()
 ​
 # 绘制决策边界
 plot_decision_boundary(X_train, y_train, svm_model, "SVM Decision Boundary (Training Set)")

通过上述代码，我们可以看到 SVM 模型在鸢尾花数据集上的分类效果，以及不同核函数对决策边界的影响。

四、SVM 的使用场景

支持向量机（SVM）是一种经典的监督学习算法，核心优势是在小样本、高维特征空间中表现稳定，能通过核函数解决线性不可分问题。其使用场景集中在对分类精度要求高、样本量适中的任务，具体如下：

4.1、文本分类与情感分析

• 文本数据天然具有高维稀疏特性（如词袋模型、TF-IDF 特征），SVM 可在高维空间中高效找到分类超平面，适合垃圾邮件识别、新闻主题分类、商品评论情感极性判断等场景。

• 例如：早期垃圾邮件过滤系统常采用 SVM + 线性核的组合，在特征维度远大于样本量时仍有优异表现。

4.2、图像识别与分类

• 用于图像局部特征（如 SIFT、HOG 特征）的分类任务，比如人脸识别、手写数字识别、医学影像病灶检测

• 例如：在 MNIST 手写数字数据集上，SVM 的分类精度接近神经网络，且训练速度更快；医学领域中，可辅助识别 X 光片、CT 图像中的异常区域

4.3、生物信息学

• 处理基因序列、蛋白质结构等高维生物数据，比如基因表达谱分类（判断正常 / 病变组织）、蛋白质功能预测、DNA 序列分析

• 这类任务通常样本量小（实验成本高）、特征维度高，SVM 的小样本学习能力可有效发挥作用

4.4、异常检测

• 单类 SVM（One-Class SVM）是常用的无监督异常检测方法，通过学习正常样本的分布，识别偏离分布的异常数据

• 适合网络入侵检测（识别异常流量）、信用卡欺诈检测（发现异常交易）、工业设备故障诊断（检测异常运行数据）

4.5、模式识别

• 适用于语音识别、指纹识别、遥感图像分类等场景，可对提取的特征向量进行精准分类

• 例如：遥感图像中不同地物（植被、建筑、水体）的分类，利用 SVM 处理多光谱特征数据

4.6、小样本数据集分类

• 当训练样本数量较少时，SVM 相比神经网络等模型泛化能力更强，不易过拟合，是小样本任务的首选算法之一

4.7、SVM算法局限性与适用边界

• 不适合超大样本数据集：SVM 的训练时间复杂度随样本量增长呈指数级上升，样本量超过 10 万时，训练效率会显著下降

• 对噪声敏感：异常值会影响分类超平面的位置，需先进行数据清洗

总结

支持向量机作为机器学习领域的重要算法，以其独特的最大间隔思想和核技巧，在数据分类任务中展现出强大的能力 。它通过寻找最优超平面，巧妙地将不同类别的数据分隔开来，不仅在理论上具有深厚的数学基础，而且在实际应用中也表现出色。

从图像分类到文本分类，从文本分类到图像识别与分类、异常检测等场景，SVM 身影无处不在，为解决各种复杂的实际问题提供了有效的解决方案。