注:本文为 "多项式乘法" 相关合辑。
英文引文,机翻未校。
如有内容异常,请看原文。
Multiplying Simple Polynomials
简单多项式的乘法运算
Just as we can multiply numbers, so also we can multiply polynomials. And just as some numerical multiplication is easier than others, so it is with polynomials.
正如我们可以对数字进行乘法运算一样,我们同样可以对多项式进行乘法运算。并且和数字乘法存在难易之分一样,多项式乘法也有简单与复杂的区别。
The simplest multiplication involving polynomials is where we're taking a number through a set of parentheses.
多项式乘法中最简单的类型,是将一个数字与括号内的多项式相乘。
Polynomials
多项式运算示例
- Simplify the following: 化简下列表达式:
− 5 ( 2 x 2 ) -5(2x^{2}) −5(2x2)
All I have to do here is multiply the − 5 -5 −5 by the 2 2 2, while carrying the x 2 x^{2} x2 along for the ride:
在此处,我们只需将 − 5 -5 −5 与 2 2 2 相乘,同时保留 x 2 x^{2} x2 项即可:
− 5 ( 2 x 2 ) = ( − 5 ) ( 2 ) ( x 2 ) = − 10 x 2 \begin{align*} & -5(2x^{2}) \\ = & (-5)(2)(x^{2}) \\ = & -10x^{2} \end{align*} ==−5(2x2)(−5)(2)(x2)−10x2
We can also multiply a number through a parenthetical which contains more than one term. In such a case, the number gets multiplied onto each/all of the terms inside.
我们也可以将一个数字与括号内的多 项式相乘。在这种情况下,该数字需要与括号内的每一项分别相乘。
- Simplify the following: 化简下列表达式:
2 ( 3 x + 1 ) 2(3x + 1) 2(3x+1)
I have a number (being the 2 2 2 to the left of, or in front of, the parenthetical) that I need to take through (or, using the technical terms, "distribute over") the expression inside the parentheses (being the 3 x + 1 3x + 1 3x+1). I'll show every step:
我们需要将括号左侧的数字 2 2 2 与括号内的表达式 3 x + 1 3x + 1 3x+1 进行分配相乘 。运算的每一步骤如下:
2 ( 3 x + 1 ) = ( 2 ) ( 3 ) ( x ) + ( 2 ) ( 1 ) = ( 6 ) ( x ) + 2 = 6 x + 2 \begin{align*} 2(3x + 1) = & (2)(3)(x) + (2)(1) \\ = & (6)(x) + 2 \\ = & 6x + 2 \end{align*} 2(3x+1)===(2)(3)(x)+(2)(1)(6)(x)+26x+2
At this point, I'm left with two un-like terms, so I cannot combine or simplify any further. My answer is:
此时表达式中剩余两个非同类项 ,无法进一步合并或化简。最终结果为:
6 x + 2 6x + 2 6x+2
You may already have seen this sort of computation when you learned about simplifying with parentheses.(You likely won't need to use so many steps as I did above, at least not once you're comfortable with the process, and your instructor almost certainly won't be expecting this much. I'm being overly complete in this lesson in hopes that, by the time you're done, you will be sure of what's going on and will feel comfortable with the process.)
你在学习含括号表达式的化简时,可能已经接触过此类运算。(当你熟练掌握该运算流程后,就无需写出上述所有步骤,你的授课老师通常也不会要求步骤如此详尽。本文将步骤全部列出,是为了帮助你清晰理解运算过程,最终熟练掌握该方法。)
Moving up in complexity, we can multiply two single-term polynomials (called "monomials").
进一步提高运算复杂度,我们可以计算两个单项式(仅含一项的多项式)的乘积。
- Simplify 化简表达式
( 5 x 2 ) ( − 2 x 3 ) (5x^{2})(-2x^{3}) (5x2)(−2x3)
I've already done this type of multiplication when I was first learning about exponents, negative numbers, and variables. I'll apply the rules that I already know, being careful to carry the "minus" sign along with its number (being the 2 2 2):
在初次学习指数、负数和变量相关知识时,你可能已经接触过此类乘法运算。我们可以运用已掌握的运算法则进行计算,注意保留数字 2 2 2 前面的负号:
( 5 x 2 ) ( − 2 x 3 ) = ( 5 ) ( x 2 ) ( − 2 ) ( x 3 ) = ( 5 ) ( − 2 ) ( x 2 ) ( x 3 ) = ( − 10 ) ( x 2 + 3 ) = − 10 x 5 \begin{align*} (5x^{2})(-2x^{3}) = & (5)(x^{2})(-2)(x^{3}) \\ = & (5)(-2)(x^{2})(x^{3}) \\ = & (-10)(x^{2+3}) \\ = & -10x^{5} \end{align*} (5x2)(−2x3)====(5)(x2)(−2)(x3)(5)(−2)(x2)(x3)(−10)(x2+3)−10x5
I can't simplify any further, so I'm done. My answer is:
表达式无法进一步化简,运算结束。最终结果为:
− 10 x 5 -10x^{5} −10x5
Usually (and in contrast to the exercise just completed), a monomial that's going to be taken through a parenthetical doesn't have parentheses around it. Instead, the multiplication is indicated simply by the "juxtaposition" of the monomial with (that is, by putting the monomial right next to) the parenthetical expression. This is called "multiplication by juxtaposition", and it looks like this:
通常情况下(与上例不同),与括号内多项式相乘的单项式本身不带括号。此时乘法运算通过单项式与括号表达式相邻放置的方式表示,这种形式被称为"并列乘法",示例如下:
- Simplify 化简表达式
− 3 x ( 1 − x ) -3x(1 - x) −3x(1−x)
I'll need to be careful with my "minus" signs.
计算时需要注意负号的处理:
− 3 x ( 1 − x ) = − 3 x ( 1 ) + ( − 3 x ) ( − x ) = − 3 x + ( + 3 ) ( x ) ( + x ) = − 3 x + 3 x 2 \begin{align*} -3x(1 - x) = & -3x(1) + (-3x)(-x) \\ = & -3x + (+3)(x)(+x) \\ = & -3x + 3x^{2} \end{align*} −3x(1−x)===−3x(1)+(−3x)(−x)−3x+(+3)(x)(+x)−3x+3x2
A monomial can be multiplied through longer polynomials, too.
单项式同样可以与项数更多的多项式相乘。
- Simplify 化简表达式
− 3 x ( 4 x 2 − x + 10 ) -3x(4x^{2} - x + 10) −3x(4x2−x+10)
To do this multiplication, I have to distribute the − 3 x -3x −3x through the parentheses:
计算该乘积时,需要将 − 3 x -3x −3x 与括号内的每一项分别相乘:
− 3 x ( 4 x 2 − x + 10 ) = − 3 x ( 4 x 2 ) + ( − 3 x ) ( − x ) + ( − 3 x ) ( + 10 ) = ( − 12 ) ( x 1 + 2 ) + ( 3 ) ( x 1 + 1 ) + ( − 30 ) ( x ) = − 12 x 3 + 3 x 2 − 30 x \begin{align*} -3x(4x^{2} - x + 10) = & -3x(4x^{2}) + (-3x)(-x) + (-3x)(+10) \\ = & (-12)(x^{1+2}) + (3)(x^{1+1}) + (-30)(x) \\ = & -12x^{3} + 3x^{2} - 30x \end{align*} −3x(4x2−x+10)===−3x(4x2)+(−3x)(−x)+(−3x)(+10)(−12)(x1+2)+(3)(x1+1)+(−30)(x)−12x3+3x2−30x
Content Continues Below
下文继续
The next step up in complexity is the multiplication of one two-term polynomial by another two-term polynomial (that is, one binomial by another binomial). This is the simplest of the "multi-term times multi-term" cases. There are actually three ways to do this. Since this is one of the most common polynomial multiplications that you likely will be doing, I'll spend a fair amount of time on this.
复杂度更高的一种多项式乘法,是两个二项式(含两项的多项式)之间的乘法运算。这是"多项 × 多项"类型中最简单的情况,共有三种计算方法。由于这是你在学习中最常接触的多项式乘法类型之一,本文将对此展开详细讲解。
- Simplify 化简表达式
( x + 3 ) ( x + 2 ) (x + 3)(x + 2) (x+3)(x+2)
The first way I can do this multiplication is by working "horizontally" (this is the method that I was taught back in high school). Doing so, I will have to distribute twice, taking each of the terms in the first parentheses "through" each of the terms in the second parentheses.
第一种方法是横向展开法 (这是我高中阶段学习的方法)。使用该方法需要进行两次分配运算,将第一个括号内的每一项与第二个括号内的每一项分别相乘:
( x + 3 ) ( x + 2 ) = ( x + 3 ) ( x ) + ( x + 3 ) ( + 2 ) = x ( x ) + 3 ( x ) + x ( + 2 ) + 3 ( + 2 ) = x 2 + 3 x + 2 x + 6 = x 2 + 5 x + 6 \begin{align*} (x + 3)(x + 2) = & (x + 3)(x) + (x + 3)(+2) \\ = & x(x) + 3(x) + x(+2) + 3(+2) \\ = & x^{2} + 3x + 2x + 6 \\ = & x^{2} + 5x + 6 \end{align*} (x+3)(x+2)====(x+3)(x)+(x+3)(+2)x(x)+3(x)+x(+2)+3(+2)x2+3x+2x+6x2+5x+6
This horizontal multiplication, while mathematically valid, is probably the most difficult and error-prone way to do this multiplication. The "vertical" method is much simpler. Think back to when you were first learning about multiplication. When you did small numbers, it was simplest to work horizontally:
这种横向乘法虽然在数学上是成立的,但却是三种方法中难度最高、最容易出错的一种。竖式乘法 的计算过程则简便得多。回想你初学乘法运算时的场景:计算较小数字的乘积时,横向计算最为便捷:
3 × 4 = 12 3 \times 4 = 12 3×4=12
But when you got to larger numbers, you stacked the numbers vertically and, working from right to left, took one digit at a time from the lower number and multiplied it, right to left, across the top number. For each digit in the lower number (first the ones digit, then the tens digits, then the hundreds digits, and so forth), you formed a new row underneath, stepping the rows off to the left as you worked from right-most digit to left-most digit in the lower number. Then you added down.
但计算较大数字的乘积时,你会将数字竖式排列,从右至左依次用下方数字的每一位,与上方数字的每一位相乘。下方数字的每一位(先个位、再十位、后百位,以此类推)与上方数字相乘后,都会得到一个新的数字行,且新行的位置会随下方数字的位数从右到左逐步向左偏移。最后将所有数字行纵向相加即可得到结果。
For instance, you would probably not want to try to multiply 121 121 121 by 32 32 32 horizontally, but it's easy when you do it vertically:
例如,计算 121 × 32 121 \times 32 121×32 时,横向计算会非常繁琐,而竖式计算则十分简便:
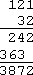
You can multiply polynomials in this same manner, so here's the same exercise as above, but done "vertically" this time:
多项式乘法同样可以采用这种竖式计算的方式,以下是上例的竖式计算过程:
- Simplify 化简表达式
( x + 3 ) ( x + 2 ) (x + 3)(x + 2) (x+3)(x+2)
I need to be sure to do my work very neatly. First, I'll set up the multiplication:
计算时需要保证书写工整。首先,列出竖式乘法的形式:
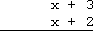
...and then I'll multiply:
随后进行分步计算:
Multiply the bottom + 2 +2 +2 by the top + 3 +3 +3, and carry down the + 6 +6 +6:
用下方的 + 2 +2 +2 乘以上方的 + 3 +3 +3,得到结果 + 6 +6 +6 并写下:
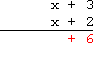
Multiply the bottom + 2 +2 +2 by the top x x x, and carry down the + 2 x +2x +2x:
用下方的 + 2 +2 +2 乘以上方的 x x x,得到结果 + 2 x +2x +2x 并写下:
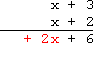
Multiply the bottom x x x by the top + 3 +3 +3, and carry down the + 3 x +3x +3x:
用下方的 x x x 乘以上方的 + 3 +3 +3,得到结果 + 3 x +3x +3x 并写下:
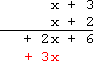
Multiply the bottom x x x by the top x x x, and carry down the x 2 x^{2} x2:
用下方的 x x x 乘以上方的 x x x,得到结果 x 2 x^{2} x2 并写下:
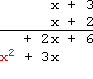
Draw a horizontal line below the two new rows:
在两行计算结果下方绘制一条横线:
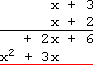
Carry the x 2 x^{2} x2 down to the bottom:
将 x 2 x^{2} x2 项下移至横线下方:
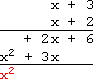
Add the + 2 x +2x +2x and the + 3 x +3x +3x, bringing down a + 5 x +5x +5x:
将 + 2 x +2x +2x 与 + 3 x +3x +3x 相加,得到 + 5 x +5x +5x 并写下:
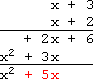
Carry the + 6 +6 +6 down to the bottom:
将 + 6 +6 +6 项下移至横线下方:
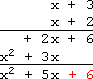
The completed vertical multiplication:
竖式乘法运算完成:
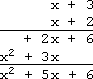
As you can see, I got the same answer working vertically as when I multiplied horizontally:
可以看到,竖式乘法得到的结果与横向乘法完全一致:
x 2 + 5 x + 6 x^{2} + 5x + 6 x2+5x+6
But the vertical method kept track of the signs, etc, for me, which made the process much less painful.
但竖式乘法能够更清晰地处理符号等细节,从而大幅降低计算难度。
Multiplying Binomials: "foil" (and a warning)
二项式乘法:"FOIL 法则"(及注意事项)
What is "foil"?
什么是"FOIL 法则"?
foil is a special method of polynomial multiplication, useful ONLY for a two-term polynomial times another two-term polynomial. The letters f-o-i-l come from the words "first", "outer", "inner", "last", and are a memory device for helping you remember how to multiply horizontally, without having to write out the distribution like I did on the previous page, and without dropping any terms or signs.
FOIL 法则是一种专门用于二项式 × 二项式的多项式乘法技巧。字母 F-O-I-L 分别对应英文单词 "first(首项)""outer(外项)""inner(内项)""last(末项)"。该法则可帮助你快速完成横向乘法运算,无需像上一节那样完整写出分配过程,同时也能避免遗漏项或符号错误。
The FOIL Method
FOIL 法则运算步骤
Below is a graphic displaying what foil stands for:
下图直观展示了 FOIL 法则的含义:
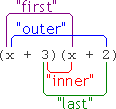
In other words, foil tells you to multiply the first terms in each of the parentheses, then multiply the two terms that are on the "outside" (that is, the two terms which are furthest from each other), then the two terms that are on the "inside" (that is, the two terms which are closest to each other), and then the last terms in each of the parentheses.
具体来说,FOIL 法则要求你依次计算:两个括号内的首项 之积、两个括号内的外项 之积(即距离彼此最远的两项)、两个括号内的内项 之积(即距离彼此最近的两项)、两个括号内的末项之积。
Using the example from the previous page, foil works like this:
以下运用 FOIL 法则计算上一节的例题:
- Use foil to simplify 运用 FOIL 法则化简表达式
( x + 3 ) ( x + 2 ) (x + 3)(x + 2) (x+3)(x+2)
Okay; the instructions specify the method I have to use, so here goes:
题目指定了计算方法,运算过程如下:
"first": 首项 :
( x ) ( x ) = x 2 (x)(x) = x^{2} (x)(x)=x2
"outer": 外项 :
( x ) ( + 2 ) = + 2 x (x)(+2) = +2x (x)(+2)=+2x
"inner": 内项 :
( + 3 ) ( x ) = 3 x (+3)(x) = 3x (+3)(x)=3x
"last": 末项 :
( + 3 ) ( + 2 ) = + 6 (+3)(+2) = +6 (+3)(+2)=+6
Adding the results of the four multiplications together, and combining the two "like" terms in the middle, I get:
将四次乘法运算的结果相加,并合并中间的两个同类项,可得:
x 2 + 2 x + 3 x + 6 = x 2 + 5 x + 6 \begin{align*} & x^{2} + 2x + 3x &+ 6 \\ = & x^{2} + \quad 5x &+ 6 \end{align*} =x2+2x+3xx2+5x+6+6
This is the same answer as we got when we multiplied horizontally and vertically.
该结果与横向乘法、竖式乘法的计算结果完全一致。
Many instructors in later math classes come to hate "foil" because it often seems to serve mostly to confuse students when they reach more advanced material. Unfortunately, foil tends to be taught in earlier algebra courses as "the" way to multiply all polynomials, which is clearly not true. (As soon as either one of the polynomials has more than a "first" and "last" term in its parentheses, you're hosed if you try to use foil, because those terms won't "fit".)
许多教授高阶数学课程的老师都不太推崇 FOIL 法则,因为当学生接触更复杂的知识点时,该法则往往会造成混淆。但遗憾的是,在初等代数课程中,FOIL 法则常被当作所有多项式乘法的通用方法来教授,而这显然是错误的。(只要其中任意一个多项式的项数超过两项,FOIL 法则就不再适用,因为无法对"首项、外项、内项、末项"进行定义。)
And foil is, essentially, just a means of keeping track of what you're doing when you're multiplying horizontally. But, for multiplications of larger numbers, you already know that vertical is the way to go. It's the same in algebra. When multiplying larger polynomials, just about everybody switches to vertical multiplication; it's just so much easier to use.
本质上,FOIL 法则只是横向乘法的一种辅助记忆工具。但正如计算大数乘积时你会选择竖式乘法一样,在代数运算中,当多项式的项数增多时,几乎所有人都会选择竖式乘法------因为这种方法的使用难度更低。
If you want to use foil, that's fine, but (warning!) keep its restriction in mind: you can ONLY use it for the special case of multiplying two binomials. You can NOT use it at ANY other time!
如果你想使用 FOIL 法则,这本身无可厚非,但需要注意 其适用范围:该法则仅 适用于两个二项式相乘的特殊情况,任何其他情况下均不可使用!
- Simplify 化简表达式
( x − 4 ) ( x − 3 ) (x - 4)(x - 3) (x−4)(x−3)
The instructions don't tell me what method I have to use for this multiplication, so I'll go vertical:
题目未指定计算方法,此处采用竖式乘法:
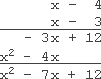
So my answer is:
最终计算结果为:
x 2 − 7 x + 12 x^{2} - 7x + 12 x2−7x+12
Using foil would give the same answer:
使用 FOIL 法则也能得到相同结果:
"first": 首项 :
( x ) ( x ) = x 2 (x)(x) = x^{2} (x)(x)=x2
"outer": 外项 :
( x ) ( − 3 ) = − 3 x (x)(-3) = -3x (x)(−3)=−3x
"inner": 内项 :
( − 4 ) ( x ) = − 4 x (-4)(x) = -4x (−4)(x)=−4x
"last": 末项 :
( − 4 ) ( − 3 ) = + 12 (-4)(-3) = +12 (−4)(−3)=+12
result: 计算结果:
( x 2 ) + ( − 3 x ) + ( − 4 x ) + ( + 12 ) = x 2 − 7 x + 12 \begin{align*} &(x^{2}) + (-3x) + (-4x) &+ (+12)\\ = & x^{2} \qquad \qquad -7x&+ 12 \end{align*} =(x2)+(−3x)+(−4x)x2−7x+(+12)+12
But multiplying vertically takes less time, space, and care than does multiplying with foil. When I first encountered vertical multiplication of polynomials, I immediately switched to this method.
但竖式乘法相比 FOIL 法则,耗时更短、占用书写空间更少、对计算细节的要求更低。我在初次接触多项式竖式乘法时,就立刻选择了这种方法。
Content Continues Below
下文继续
- Multiply and simplify: 计算并化简:
( x − 3 y ) ( x + y ) (x - 3y)(x + y) (x−3y)(x+y)
This multiplication looks like it might be more complicated, because of the second variable, but the process doesn't care how many terms have variables. So I can proceed as usual.
该乘法运算因包含第二个变量 y y y,看起来似乎更为复杂,但多项式乘法的运算流程与变量的数量无关,因此可以按照常规步骤计算。
Vertical multiplication gives me this:
竖式乘法计算过程如下:
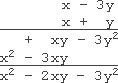
So my hand-in answer is:
最终提交的计算结果为:
x 2 − 2 x y − 3 y 2 x^{2} - 2xy - 3y^{2} x2−2xy−3y2
Using foil would give me:
使用 FOIL 法则计算过程如下:
"first": 首项 :
( x ) ( x ) = x 2 (x)(x) = x^{2} (x)(x)=x2
"outer": 外项 :
( x ) ( y ) = x y (x)(y) = xy (x)(y)=xy
"inner": 内项 :
( − 3 y ) ( x ) = − 3 x y (-3y)(x) = -3xy (−3y)(x)=−3xy
"last": 末项 :
( − 3 y ) ( y ) = − 3 y 2 (-3y)(y) = -3y^{2} (−3y)(y)=−3y2
result: 计算结果:
( x 2 ) + ( x y ) + ( − 3 x y ) + ( − 3 y 2 ) = x 2 − 2 x y − 3 y 2 \begin{align*} &(x^{2}) + (xy) + (-3xy) + (&-3y^{2})\\ =& x^{2} \qquad -2xy &- 3y^{2} \end{align*} =(x2)+(xy)+(−3xy)+(x2−2xy−3y2)−3y2
- Multiply and simplify: 计算并化简:
( 2 x − 5 ) ( 3 x + 4 ) (2x - 5)(3x + 4) (2x−5)(3x+4)
This multiplication has some slightly larger coefficients, but the process is the same. I'll work vertically:
该乘法运算的系数数值稍大,但运算流程保持不变。此处采用竖式乘法:
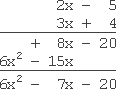
answer: 计算结果:
6 x 2 − 7 x − 20 6x^{2} - 7x - 20 6x2−7x−20
I won't bother doing the foil process for this exercise.
本例题不再展示 FOIL 法则的计算过程。
- Multiply:计算乘积:
( − 4 x − 1 ) ( 5 x − 7 ) (-4x - 1)(5x - 7) (−4x−1)(5x−7)
The factors in this product have a lot of "minus" signs, but the process remains the same:
该乘法运算的因式中包含较多负号,但运算流程保持不变:
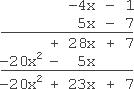
answer: 计算结果:
− 20 x 2 + 23 x + 7 -20x^{2} + 23x + 7 −20x2+23x+7
- Expand:展开表达式:
( x − 3 ) 2 (x - 3)^{2} (x−3)2
Some students will try to take a shortcut with this and, thinking that the power somehow "distributes" over the terms, they'll square each of the terms (getting an x 2 x^{2} x2 and a 9 9 9, but no middle terms with x x x's in them) and... then they'll be confused about what signs should go where.
部分学生会尝试走捷径,认为指数可以直接分配到括号内的每一项上,于是直接将各项分别平方(得到 x 2 x^{2} x2 和 9 9 9,但遗漏了含 x x x 的中间项),最终因符号和项数错误而陷入困惑。
Instead, I'm going to write out the square explicitly; the expression they gave me means the following:
正确的做法是将平方运算展开为乘法形式,原表达式等价于:
( x − 3 ) ( x − 3 ) (x - 3)(x - 3) (x−3)(x−3)
This multiplies as follows:
该表达式的乘法运算过程如下:
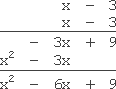
answer: 计算结果:
x 2 − 6 x + 9 x^{2} - 6x + 9 x2−6x+9
- Expand and simplify: 展开并化简:
( x + 1 3 ) ( x + 1 2 ) \left(x+\frac{1}{3}\right)\left(x+\frac{1}{2}\right) (x+31)(x+21)
Fractions? Really?!? Well, the process will work just the same with fractions as it did with whole numbers:
竟然包含分数?没关系!多项式乘法的运算流程对分数和整数完全相同:
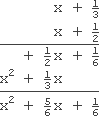
Off to the side on my scratch-paper, I add the fractions for the middle term:
在草稿纸上单独计算中间项的分数加法:
1 2 + 1 3 = 3 6 + 2 6 = 5 6 \begin{align*} & \frac{1}{2} + \frac{1}{3} \\ = & \frac{3}{6} + \frac{2}{6} \\ = & \frac{5}{6} \end{align*} ==21+3163+6265
So my simplified answer is:
化简后的计算结果为:
x 2 + 5 6 x + 1 6 x^{2} + \frac{5}{6}x + \frac{1}{6} x2+65x+61
Before we move on, please allow me reiterate what I said at the beginning of this page: "foil" works ONLY for the specific and special case of a two-term expression times another two-term expression. It does NOT apply in ANY other case. You should not rely on foil for general multiplication, and should not expect it to "work" for every multiplication, or even for most multiplications. If you only learn foil, you will not have learned all you need to know, and this will cause you problems later on down the road.
进入下一节之前,请允许我重申本节开头的内容:FOIL 法则仅 适用于"二项式 × 二项式"这一特殊情况,任何其他情况下均不适用。你不应依赖 FOIL 法则进行通用的多项式乘法运算,也不应期望它适用于全部或大部分乘法场景。如果只掌握 FOIL 法则,你并没有学会多项式乘法的全部知识,这会为后续的学习埋下隐患。
Yes, I'm ranting. But I have seen too many students be greatly hampered in their studies by an unthinking over-reliance on foil. Their instructors often never even taught them any method for multiplying other sorts of polynomials.
没错,我这番话有些啰嗦。但我确实见过太多学生,因盲目依赖 FOIL 法则而严重影响后续学习------他们的老师甚至从未教过他们其他类型多项式的乘法方法。
For your own sake, take the time to read the next page and learn how to multiply general polynomials properly.
为了你的学习效果,请认真阅读下一节内容,掌握通用多项式乘法的正确计算方法。
Multiplying General Polynomials
通用多项式乘法
Simple FOIL General
基础运算|FOIL 法则|通用运算
Sometimes (such as in calculus) you will need to multiply one multi-term polynomial by another multi-term polynomial. You can do this horizontally if you want, but there is so much room for error that I always switch over to vertical multiplication once the polynomials get past two terms in length (and usually for the binomials, too). For bigger multiplications, vertical multiplication is usually faster, and is much more likely to give you a correct answer.
在某些场景下(例如微积分运算),你需要计算两个多项多项式的乘积。虽然可以采用横向乘法,但这种方法的容错率极低。因此,当多项式的项数超过两项时,我通常会选择竖式乘法(即使是二项式乘法,我也更倾向于使用这种方法)。对于复杂的多项式乘法运算,竖式乘法的计算速度更快,且得到正确结果的概率更高。
Advanced Polynomial Multiplication
高阶多项式乘法
- Simplify 化简表达式
( 4 x 2 − 4 x − 7 ) ( x + 3 ) (4x^{2} - 4x - 7)(x + 3) (4x2−4x−7)(x+3)
Here's what the multiplication looks like when it's done horizontally:
横向乘法的计算过程如下:
( 4 x 2 − 4 x − 7 ) ( x + 3 ) = ( 4 x 2 − 4 x − 7 ) ( x ) + ( 4 x 2 − 4 x − 7 ) ( 3 ) = 4 x 2 ( x ) − 4 x ( x ) − 7 ( x ) + 4 x 2 ( 3 ) − 4 x ( 3 ) − 7 ( 3 ) = 4 x 3 − 4 x 2 − 7 x + 12 x 2 − 12 x − 21 = 4 x 3 − 4 x 2 + 12 x 2 − 7 x − 12 x − 21 = 4 x 3 + 8 x 2 − 19 x − 21 \begin{align*} & (4x^{2} - 4x - 7)(x + 3) \\ = & (4x^{2} - 4x - 7)(x) + (4x^{2} - 4x - 7)(3) \\ = & 4x^{2}(x) - 4x(x) - 7(x) + 4x^{2}(3) - 4x(3) - 7(3) \\ = & 4x^{3} - 4x^{2} - 7x + 12x^{2} - 12x - 21 \\ = & 4x^{3} - 4x^{2} + 12x^{2} - 7x - 12x - 21 \\ = & 4x^{3} + 8x^{2} - 19x - 21 \end{align*} =====(4x2−4x−7)(x+3)(4x2−4x−7)(x)+(4x2−4x−7)(3)4x2(x)−4x(x)−7(x)+4x2(3)−4x(3)−7(3)4x3−4x2−7x+12x2−12x−214x3−4x2+12x2−7x−12x−214x3+8x2−19x−21
That was painful! Now I'll do it vertically:
这个过程太繁琐了!接下来采用竖式乘法计算:
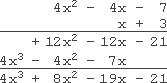
That was a lot easier! But, just as before, the answer is:
这个过程简便多了!最终计算结果与横向乘法一致:
4 x 3 + 8 x 2 − 19 x − 21 4x^{3} + 8x^{2} - 19x - 21 4x3+8x2−19x−21
- Simplify 化简表达式
( x + 2 ) ( x 3 + 3 x 2 + 4 x − 17 ) (x + 2)(x^{3} + 3x^{2} + 4x - 17) (x+2)(x3+3x2+4x−17)
I'm just going to do this one vertically; horizontally is too much trouble.
此处直接采用竖式乘法计算,横向乘法的计算量过大。
Note that, since order doesn't matter for multiplication, I can still put the " x + 2 x + 2 x+2" polynomial on the bottom for the vertical multiplication, just as I always put the smaller number on the bottom when I was doing regular vertical multiplication with just plain numbers back in grammar school.
需要注意的是,由于乘法满足交换律,在竖式乘法中,我可以将二项式 x + 2 x + 2 x+2 写在下方------就像小学阶段计算数字乘法时,总是将位数较少的数字写在下方一样。
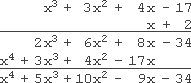
x 4 + 5 x 3 + 10 x 2 − 9 x − 34 x^{4} + 5x^{3} + 10x^{2} - 9x - 34 x4+5x3+10x2−9x−34
Content Continues Below
下文继续
- Simplify 化简表达式
( 3 x 2 − 9 x + 5 ) ( 2 x 2 + 4 x − 7 ) (3x^{2} - 9x + 5)(2x^{2} + 4x - 7) (3x2−9x+5)(2x2+4x−7)
I'll take my time, and do my work neatly:
计算时需要耐心细致,保证书写工整:
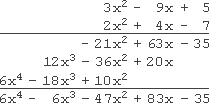
6 x 4 − 6 x 3 − 47 x 2 + 83 x − 35 6x^{4} - 6x^{3} - 47x^{2} + 83x - 35 6x4−6x3−47x2+83x−35
- Simplify 化简表达式
( x 3 + 2 x 2 + 4 ) ( 2 x 3 + x + 1 ) (x^{3} + 2x^{2} + 4)(2x^{3} + x + 1) (x3+2x2+4)(2x3+x+1)
First off, I notice that terms of these polynomials have some power (that is, degree) "gaps".
首先可以观察到,这两个多项式的项数存在次数空缺。
The first polynomial has an x 3 x^{3} x3 term, an x 2 x^{2} x2 term, and a constant term, but no x x x term; and the second polynomial has an x 3 x^{3} x3 term, an x x x term, and a constant term, but no x 2 x^{2} x2 term. When I do the vertical multiplication, I will need to leave spaces in my set-up, corresponding to the "gaps" in the degrees of the polynomials' terms, because I will almost certainly need the space.
第一个多项式包含 x 3 x^{3} x3 项、 x 2 x^{2} x2 项和常数项,但缺少 x x x 项;第二个多项式包含 x 3 x^{3} x3 项、 x x x 项和常数项,但缺少 x 2 x^{2} x2 项。在进行竖式乘法时,需要在对应次数空缺的位置留出空格------这样做可以有效避免计算错误。
(This is similar to using zeroes as "place holders" in regular numbers. You might have a thousands digit of 3, a hundreds digit of 2, and a units digit of 5, so you'd put a 0 in for the tens digits, creating the number 3,205.)
(这与数字运算中用 0 占位的原理类似。例如,一个数字的千位为 3、百位为 2、个位为 5,那么需要在十位补 0,从而得到数字 3205。)
Here's what that looks like:
竖式乘法的书写形式如下:
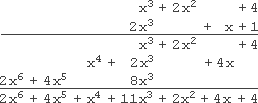
See how I needed the gaps? See how it helped that I had everything lined up according to the term's degree? If I hadn't left gaps when writing out my original factors, my terms could easily have become misaligned in the rows below. By taking the time to write things out explicitly neatly, I saved myself from many needless difficulties.
可以看到,空格的预留是非常必要的,它能保证同类项在纵向对齐。如果在书写因式时没有预留空格,下方计算结果的各项很容易出现错位。花时间规范书写格式,能够帮你避免许多不必要的麻烦。
My answer is:
最终计算结果为:
2 x 6 + 4 x 5 + x 4 + 11 x 3 + 2 x 2 + 4 x + 4 2x^{6} + 4x^{5} + x^{4} + 11x^{3} + 2x^{2} + 4x + 4 2x6+4x5+x4+11x3+2x2+4x+4
I did have one professor who could just look at huge polynomial products, and somehow keep all the terms straight while he did the multiplications and additions in his head. He'd write down the terms one-by-one, starting from the highest degree to the lowest, going straight from the original product to the final answer. He seriously freaked us all out!
我曾经有一位教授,他只需要扫一眼复杂的多项式乘积,就能在脑海中完成所有乘法与加法运算,并且准确无误地梳理出每一项。他会按照次数从高到低的顺序,直接写出最终结果的每一项,整个过程一气呵成。当时这一幕让我们所有人都惊叹不已!
While you may aspire to such proficiency, don't reject the tool of vertical multiplication, at least when you're getting started. Don't try to freak out your classmates until you're really good at using the regular methods.
虽然你可能也希望达到这样的熟练程度,但至少在初学阶段,请务必掌握竖式乘法这一工具。在你真正精通常规计算方法之前,不必急于尝试这种"惊艳全班"的技巧。
via:
-
Multiplying Simple Polynomials
https://www.purplemath.com/modules/polymult.htm -
FOIL-ing binomials & multiplying vertically: Explained!
https://www.purplemath.com/modules/polymult2.htm -
FOIL won't work, so how do you multiply bigger polynomials?
https://www.purplemath.com/modules/polymult3.htm