课件例题
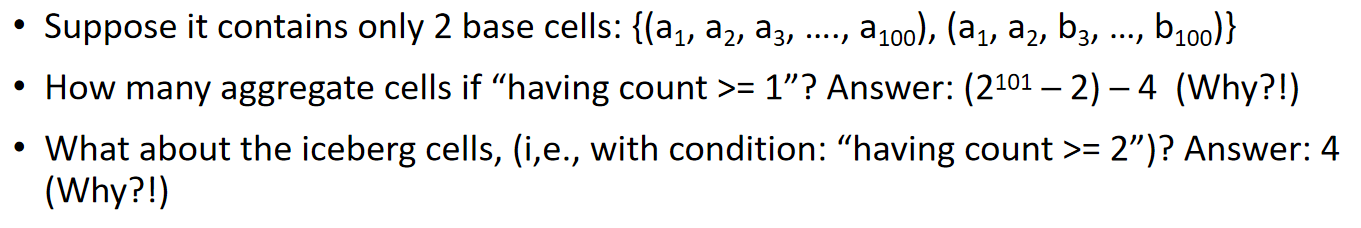
这个题如此抽象,先看一下基本概念:


有两种情况:count>=1,count>=2
理解一下,这里count>=1时,相当于把每个基础单元格看作集合,然后求出这个集合的所有真子集,然后取并集



发现
数据立方体count>=k(k>=2,k=1的时候还是用容斥原理吧)时聚合单元的个数,等于挖掘频繁项集支持度>=k的个数+1(ALL的情况)
可以这样理解,如果是(a1,b1,*,*)这种情况,就是不考虑后面的项目,相当于只有(a1,b1)

对于课件中count>=2的这一问,1-频繁项集a1,a2,2-频繁项集a1a2,再加上ALL,共4个
一个练习题

按照挖掘频繁项集的思路:1-频繁项集:a1,b1,c1,共3个
2-频繁项集a1b1,a1c1,共2个
3-频繁项集,没有
再加上(*,*,*,*,*,*),一共6个
如果是count>=1呢?
T1T2T3都有2^6 ,3*2^6
T1T2共有(a1,b1),2^2;T2T3共有(a1),2;T1T2共有(a1,c1),2^2
T1T2T3共有a1,2
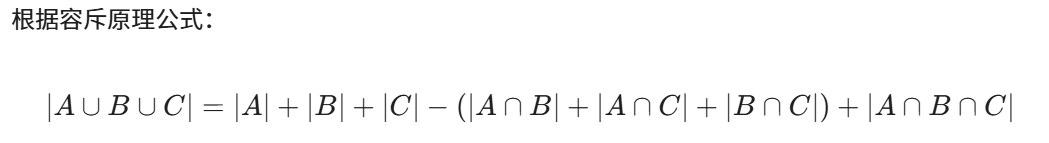

根据课件中讲的,还要减去basecell,也就是184-3 = 181
闭立方体
冰山立方体与闭立方体常常比较

还是这个例题:

计算冰山立方体的数目与闭立方体的数目
冰山立方体的结果是

闭立方体的计算结果是
(a1)(a1,b1)(a1,c1)
在冰山立方体的基础上,找到最长的项集(a1,b1),(a1,c1),如果它分别的子集(a1),(b1)和(a1),(c1)的count值跟它一样,就把子集去掉
另外,all相当于空集的情况
因为(a1)的子集有空集,且all的count也是3,于是all也被剔除掉了
闭立方体同样可以用闭频繁项集理解:

刚刚的闭立方体是无损压缩,还有个概念是最大立方体,是有损压缩
最大立方体
用之前的例子:

也是先算冰山立方体

最大立方体只有两个记录:(a1,b1),(a1,c1)
同样用频繁项集的概念来理解,最大立方体对应最大频繁项集,也就是要去掉频繁项集的子集(a1,b1)包含子集(a1)(b1)空集,(a1,c1)包含子集(a1)(c1)空集都去掉
闭立方体与最大立方体的区别
闭立方体在剔除的时候,只剔除子集中与这个项集count数目一致的,而最大立方体,不管子集的大小,都剔除

这里立方体定义的时候与项集不同
立方体定义的,父集是(a1,*,*,*),它的子集是(a1,b1,*,*)等
而我刚刚说的子集是项集这个集合的概念,(a1,b1)的子集是(a1)(b1)
对于(*,*,*,*)这种all的情况,相当于空集
(个人认为用项集的概念转化一下就更好理解,希望能有原始的更好的理解方法)