上周进行了线性慧慧的学习，本周将学习分类其中输出变量Y只能输出一小部分可能得值之一，而不是无限范围内的任意可能值，线性回归不是分类问题的良好算法，本周将 学习逻辑回归，这是当今最流行，最广泛的学习算法，之一
分类的例子，判断一个邮件是否为垃圾邮件
判断在线金融交易是否欺诈，
肿瘤分类是恶性或者良性
在这些例子中，希望输出的结果只有两个可能值之一，是或者否，这种两个可能输出的分类叫做二元分类，二元指的是两个可能的类别，或者可能得分类，其中可用no,或者 yes来表示，也可以用 FALSE,TRUE .0 ,1来表示 其中都可以称之为正类或者负类。
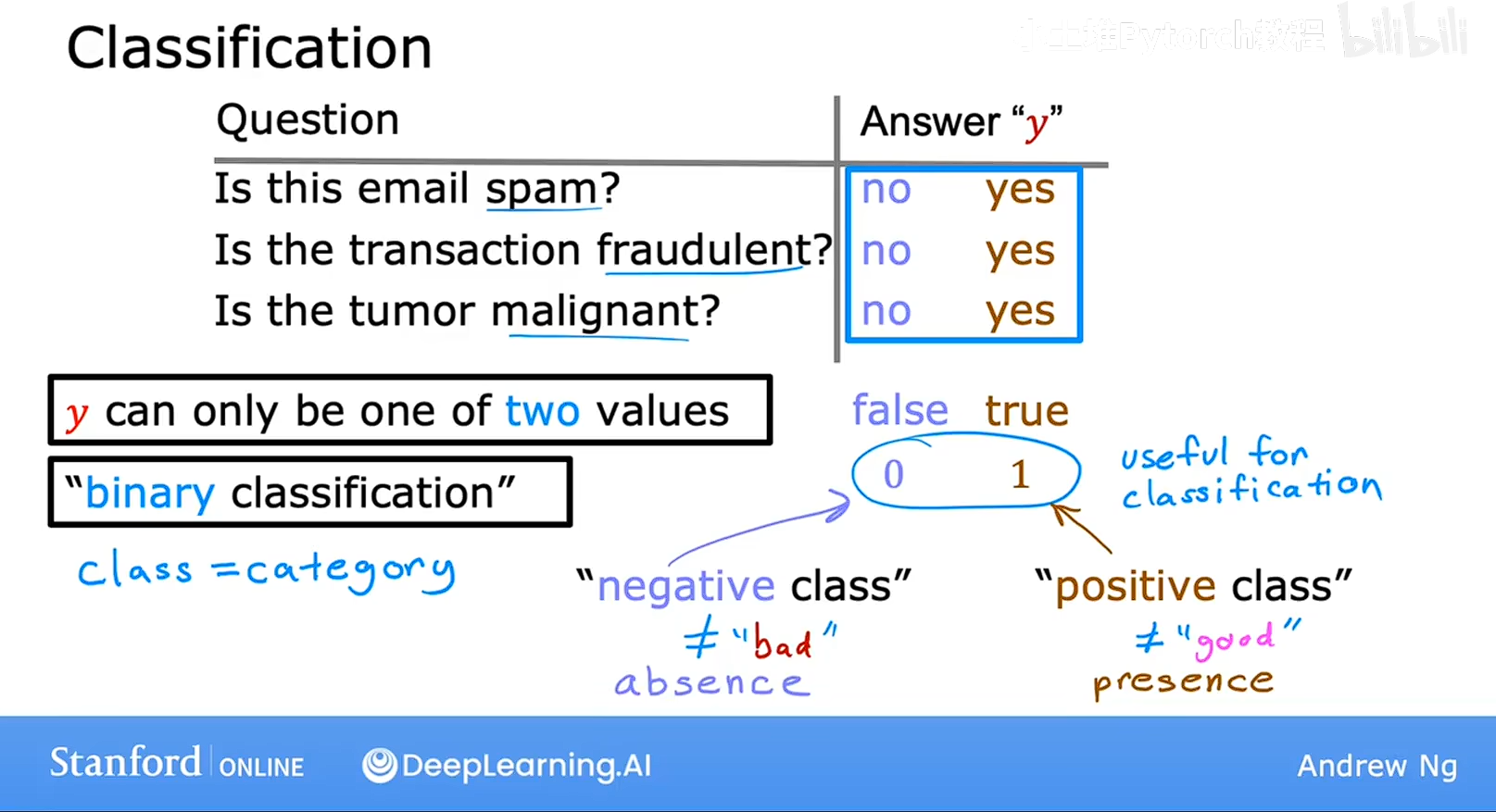
那么如何构建一个分类算法呢？
我们看一下关于预测肿瘤的数据集
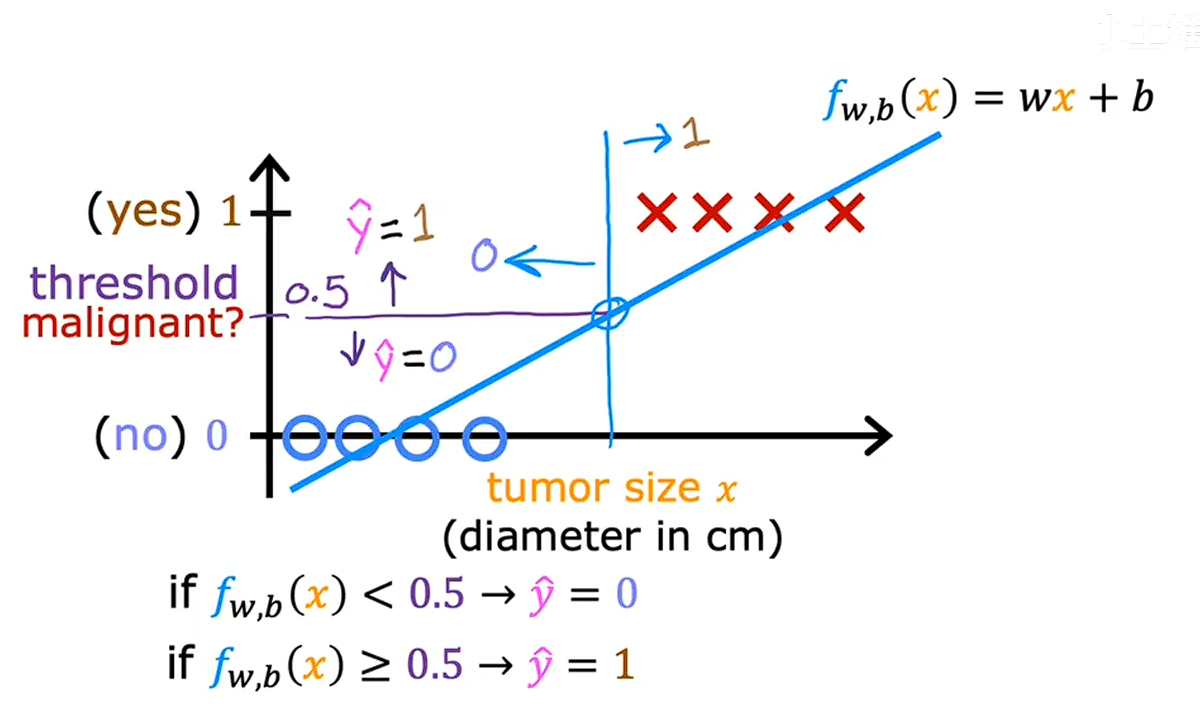
其中横轴表示肿瘤的大小，纵轴表示我们的标签，我如果我们用线性回归处理这个问题，并在算法中去0.5的阈值在这里画一条垂线用于我们决策，我们叫这个线为决策线，小于0.5则输出0大于0.5则输出1，这样看起来还可以但是有问题，看些下图，
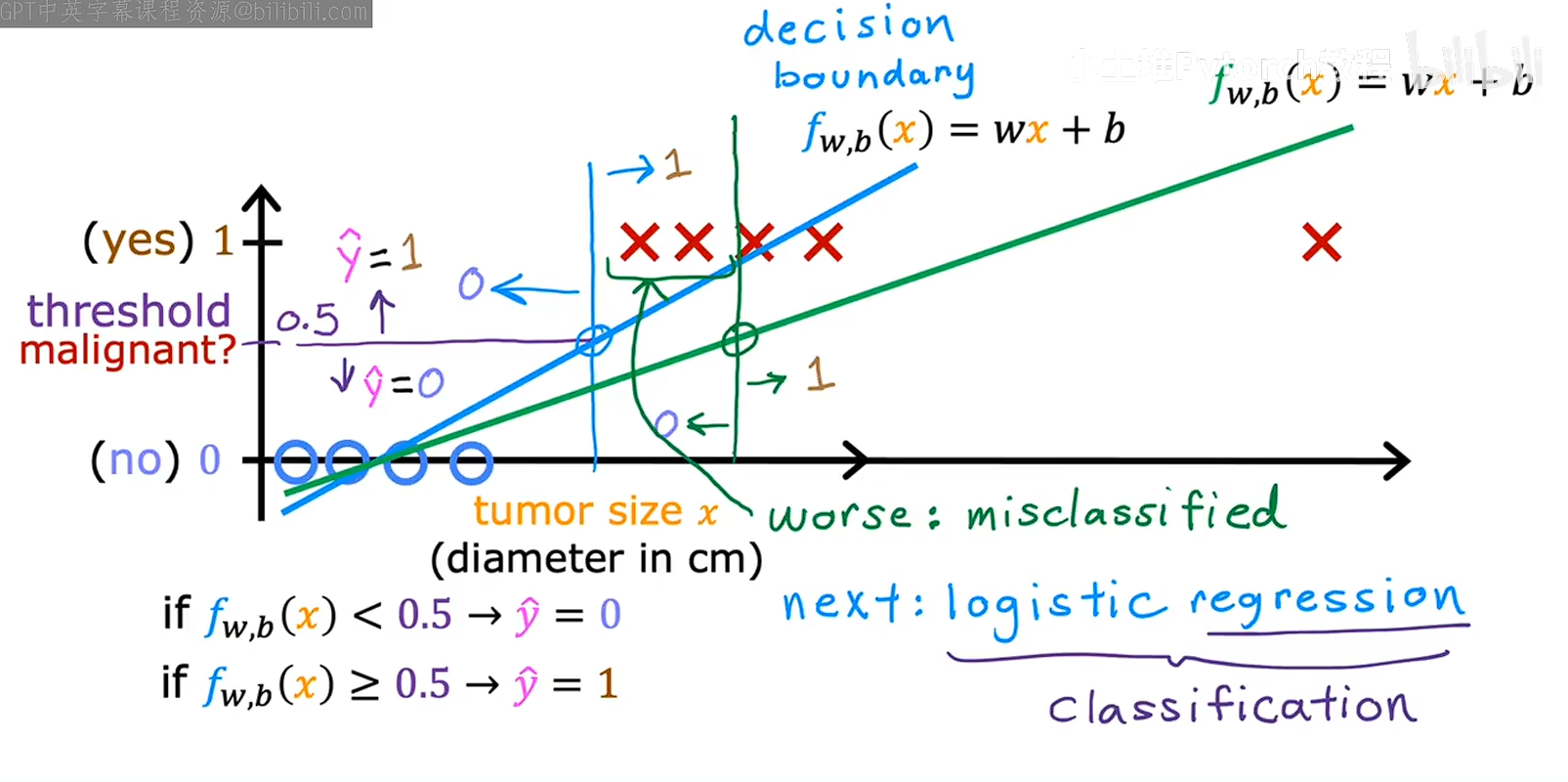
如果此时出现了一个size很大的树数据，我们延长横轴，这个时候回归线会向右偏移，理所档案，决策线也会向右偏移，如图绿色的线是偏移之后的线，可以用这条决策线去分类绝不是很好，后面将学习逻辑回归，其中输出值始终在0和1之间算法将避免上图中我们看到的问题，逻辑回归这个名字会令人疑惑尽管他包含回归但是却用于分类，名字是历史原因而明明的
逻辑回归
我们谈谈逻辑回归，这可能是世界上最广泛的分类算法了，
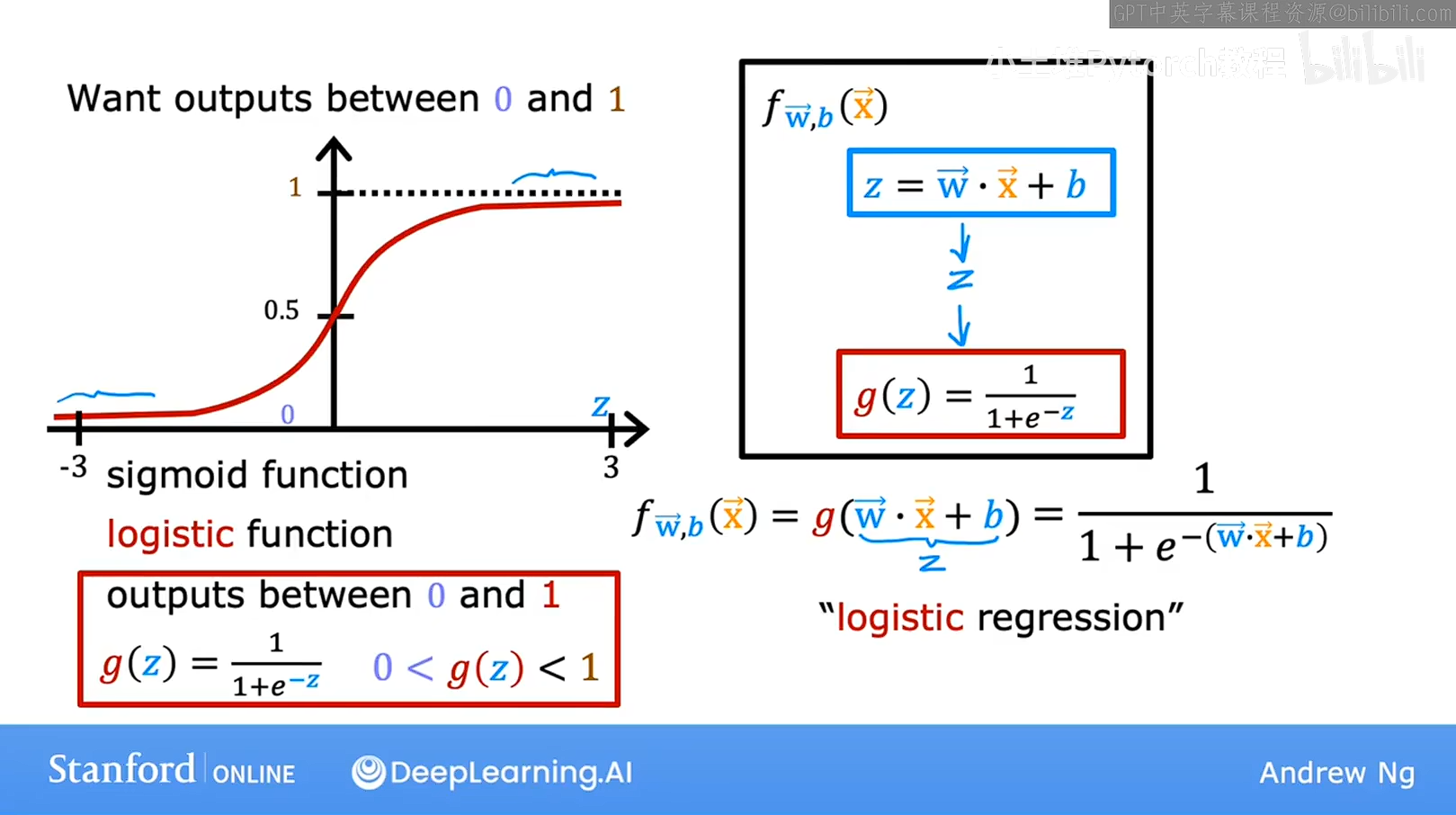
线性回归并不适合我们想要一个函数是一个S形的，这个函数输出的结果是0-1之间的数字，然后我们取一个阈值，大于这个阈值输出0小于这个阈值输出1
这个函数就是Sigmoid function 有时称为逻辑函数
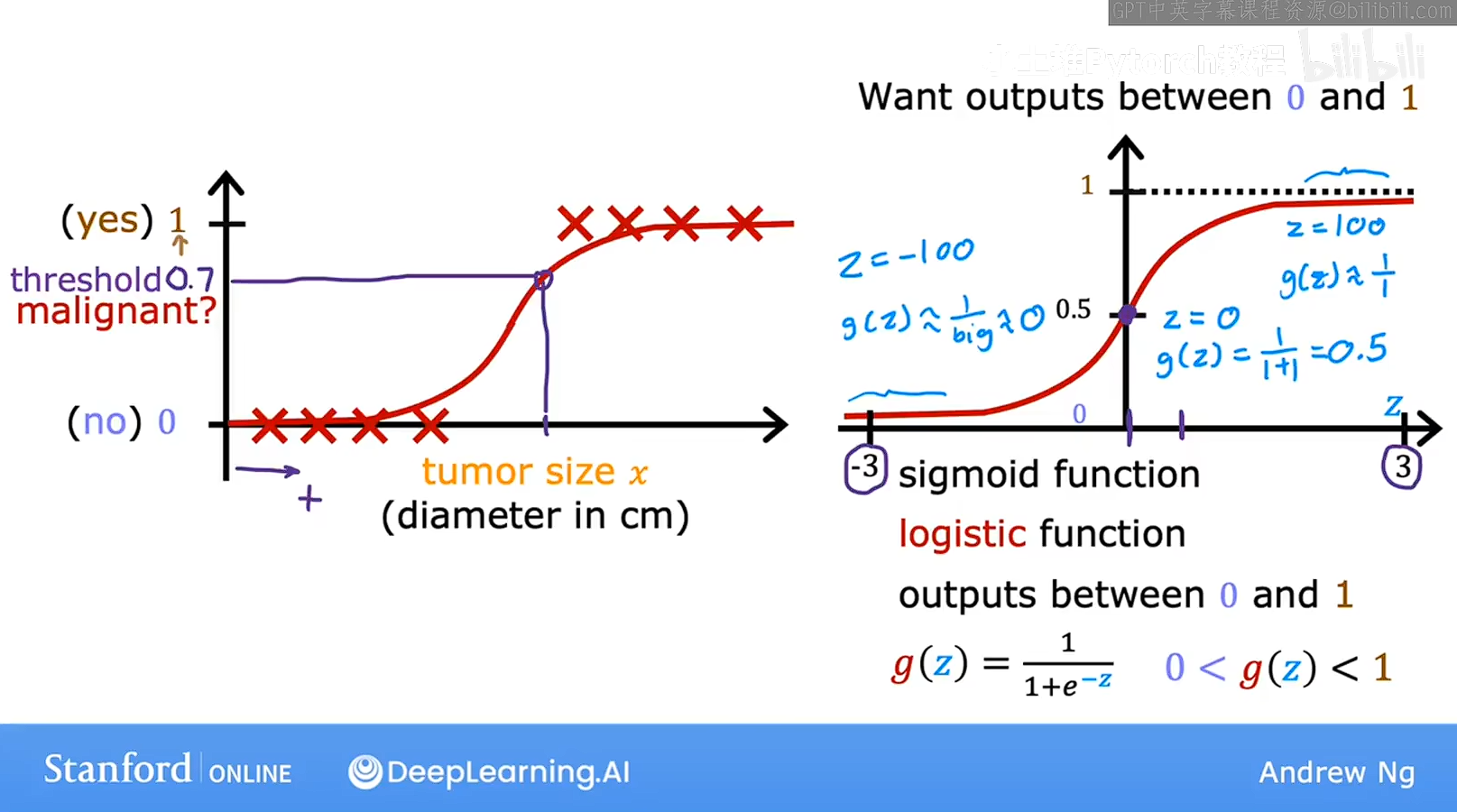这个函数当z非常大的时候，e的负Z次放会非常小指数级变小，函数趋近与1，正类
当z非常小，分母就会变大，函数趋近与0，是父类
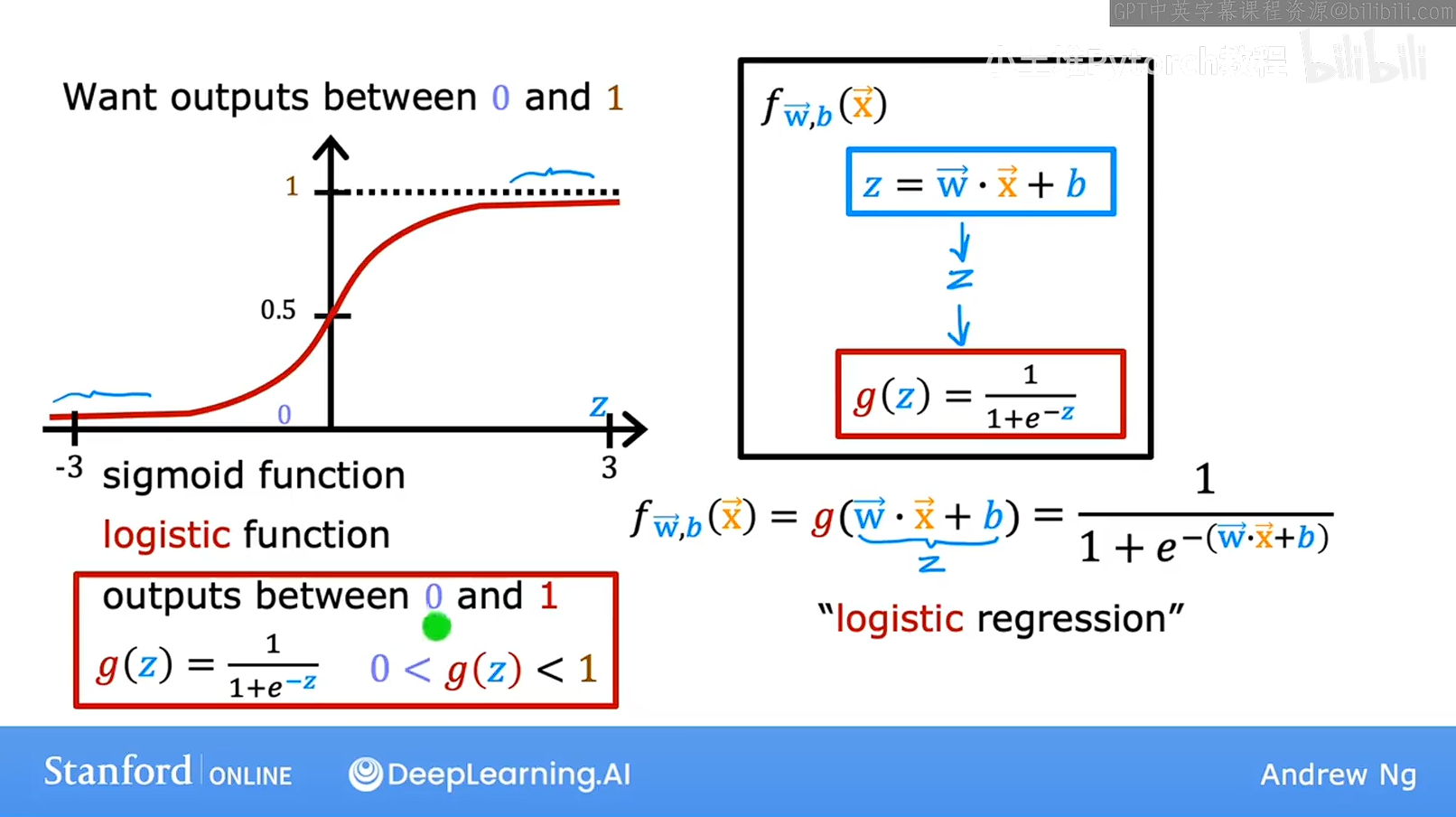
对于logistic funtion,这个是最终的函数，两个函数是一样的，但是这个函数更具体一下，就是把线性回归的输出，带入到逻辑回归总，就是相当于把线性回归外面套了一个壳子，把线性回归的输出压缩，为0-1，这个壳子就是sigmoiid function,结果就是logistics function
决策边界
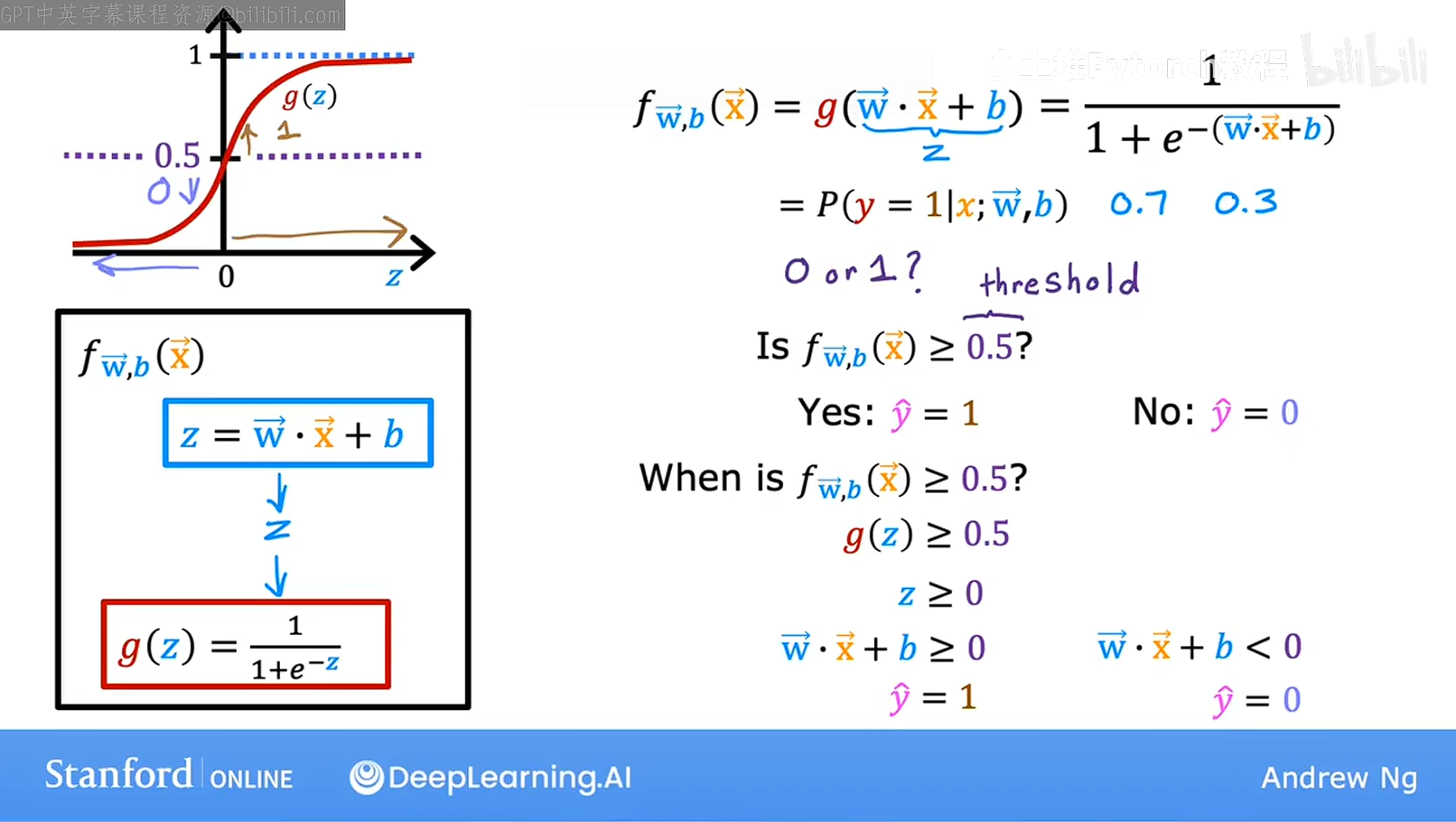
由于逻辑回归的的函数是0-1的区间的，我们要他输出0或者1两个值，有什么方法呢？
我们可以设定一个阈值，当数值大于这个阈值的时候输出1，当数值小于这个阈值的时候，输出0我们用一个常见的0.5为阈值，当值大于0.5的时候模型输出1，当值小于0.5的时候模型输出0，我们观察函数的图象，
发现，当Z大于0的时候，函数大于0.5介于0.5-1之间，当Z小于0的时候模型小于0.5介于0-0.5，我们发现因为是嵌套的函数，W·X+b=Z, 等量代换，
当W·X+b>0输出1，W·X+b<0输出0， 那么W·X+b=0就是这个模型的决策边界，
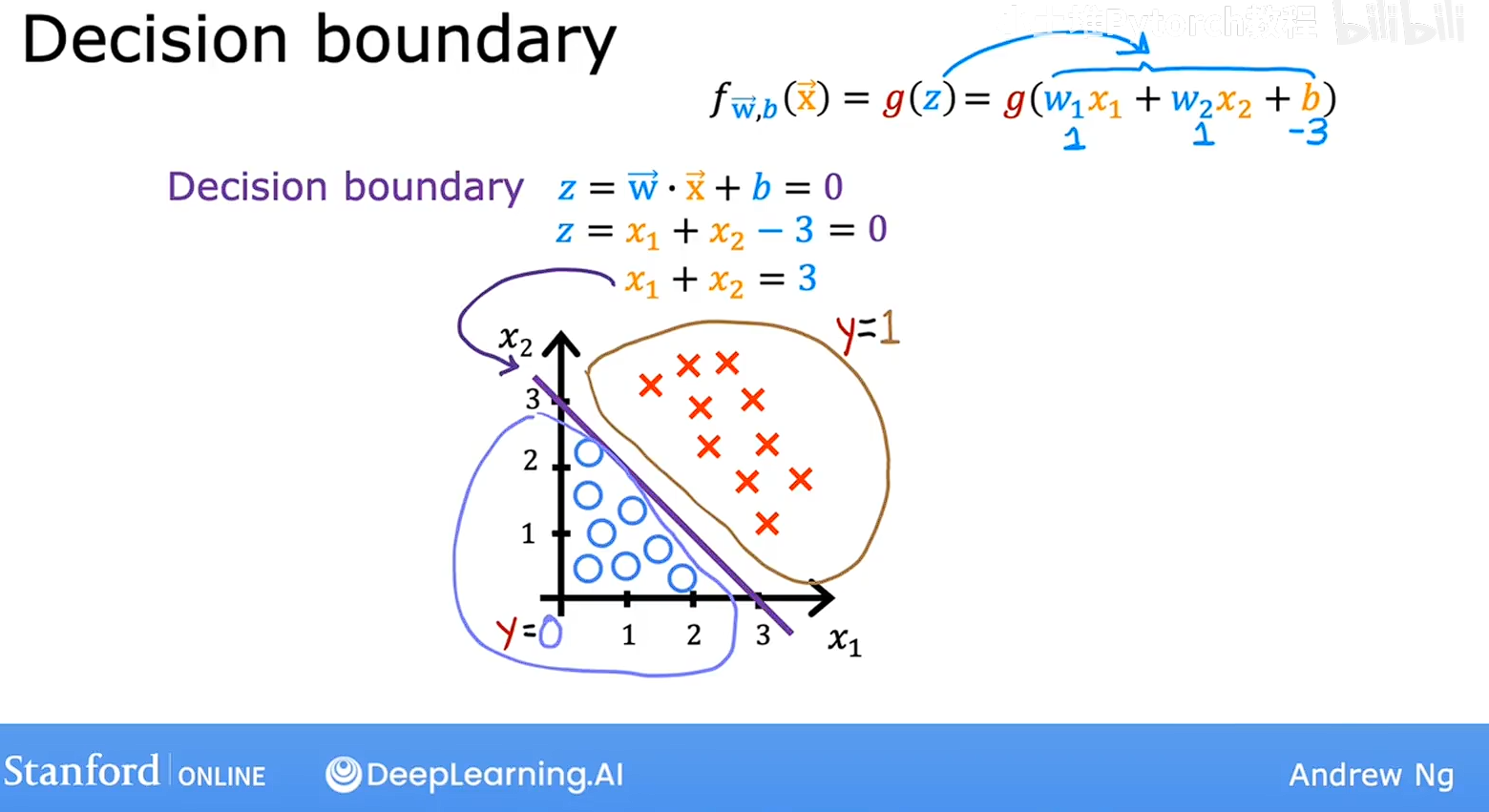
在这个模型中W1=1,W2=2,B=-3，得到x1+x2-3=0
那个这条线就是上图汇总紫色的线，如果特征X在这条线的左边则会输出0，反之则输出1，
类似的，这个模型的决策边界是一个园，当X1平方+X2平方大于1就在圆的外部，输出1，反之则输出0
还有其他的更复杂的边界例如下图
