PnP和P3P详解与Matlab 实现

一、什么是PnP

PnP = 已知 n 个 3D 点和它们在图像中的 2D 投影，求相机（或物体）的 3D 位姿。

用"点对点"的几何约束，把二维图像还原成三维位姿。

P n P 分别表示什么意思

理解

📍 一块标定板 / 工件
- 上面点的 3D 坐标已知
📷 一张图像
- 这些点的 2D 像素坐标已知

👉 PnP 要算的是：

这个物体 在空间中怎么摆的
或者相机 在什么位置、什么角度

也就是：
位置 + 姿态 = 6D Pose

二、数学推导

PnP 的数学问题定义（起点）

成像模型（PnP 的物理基础）

PnP 的核心等式（齐次形式）

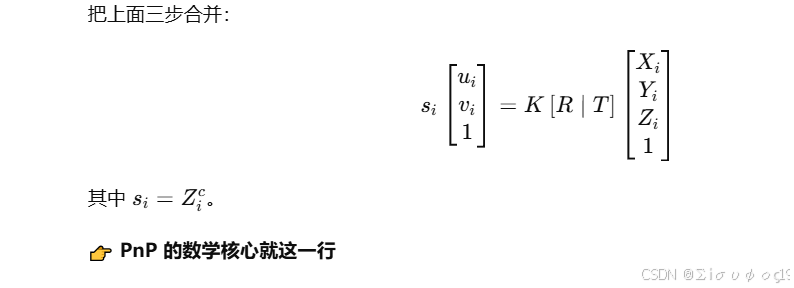
线性化（DLT 推导）

从投影矩阵分解出 R 和 T

真正的 PnP：非线性最小二乘

旋转的数学参数化（关键点）

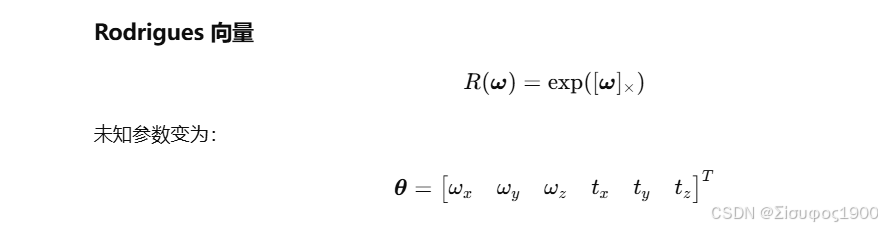
LM 优化推导（核心计算）

https://blog.csdn.net/weixin_39354845/article/details/130642106?sharetype=blogdetail&sharerId=130642106&sharerefer=PC&sharesource=weixin_39354845&spm=1011.2480.3001.8118

为什么至少需要 3 个点

三、P3P

简介

P3P是PnP的最小情形

P3P = PnP 在 n=3 时的解析几何解

PnP = 以 P3P 为初值的非线性最小二乘

本质：

P3P 的本质是：

利用三条已知射线夹角和三边长度，通过余弦定理消元，

得到一个四次多项式，其实根对应相机到三点的几何构型

计算流程

P3P 问题定义（最小情形）

关键几何转化（把问题变成三角形）

用余弦定理建立方程（核心）

消元 → 四次多项式（解析解的关键）

求解与物理筛选

由三点恢复位姿 R,T

为什么 P3P 会有多解？

几何原因：

相机与三点构成的空间四面体
关于某些平面对称 → 镜像解
三点几乎共线 / 共面 → 退化

📌 所以工程中：

P3P 只做初值
后面一定接 LM 优化（PnP）

MATLAB：P3P + LM（完整 PnP）实现

整体结构

输入：N ≥ 4 个 3D--2D 对应点 + 相机内参

↓

任选 3 点 → P3P

↓

得到 1~4 个 (R,T) 初值

↓

LM 优化（最小化重投影误差）

↓

输出最优 (R,T)

主程序（P3P_main.m）

cs 复制代码

clc; clear;

%% ========= 1. 数据 =========
% --- 世界坐标点 (>=4) ---
Pw = [
    0    0    0;
    0.1  0    0;
    0    0.1  0;
    0.1  0.1  0
];

% --- 像素点 ---
uv = [
    520 410;
    610 415;
    515 500;
    605 505
];

% --- 相机内参 ---
fx = 800; fy = 800;
cx = 640; cy = 360;
K = [fx 0 cx;
     0 fy cy;
     0  0  1];

%% ========= 2. 用前三点做 P3P =========
[R0, T0] = p3p_initial(Pw(1:3,:), uv(1:3,:), K);

%% ========= 3. LM 优化 =========
x0 = pose_to_vector(R0, T0);

opts = optimoptions('lsqnonlin',...
    'Algorithm','levenberg-marquardt',...
    'Display','iter',...
    'FunctionTolerance',1e-10);

x_opt = lsqnonlin(@(x) reproj_residual(x, Pw, uv, K), ...
                  x0, [], [], opts);

%% ========= 4. 输出 =========
[R, T] = vector_to_pose(x_opt);

disp('Optimized Rotation R =');
disp(R);
disp('Optimized Translation T =');
disp(T');

四次多项式构造函数（核心）

cs 复制代码

function coeffs = p3p_polynomial(a,b,c,ca,cb,cg)
% 返回 x 的四次多项式系数 [A B C D E]

A = (a^2 - b^2)^2 - 4*a^2*b^2*cg^2;
B = 4*(a^2 - b^2)*(b^2*(1-ca*cb) - a^2*(1-ca^2));
C = 2*( ...
    (a^2 - b^2)^2 ...
    + 2*(a^2 + b^2)*(a^2*ca^2 + b^2*cb^2 - a^2 - b^2) ...
    + 4*a^2*b^2*ca*cb*cg ...
);
D = 4*(b^2*(1-ca*cb) - a^2*(1-ca^2))*(a^2 - b^2);
E = (a^2 - b^2)^2 - 4*a^2*b^2*ca^2;

coeffs = [A B C D E];
end

P3P 初值函数

cs 复制代码

function [bestR, bestT] = p3p_initial(Pw, uv, K)

% 像素 → 单位方向
u = zeros(3,3);
for i = 1:3
    x = K \ [uv(i,:) 1]';
    u(i,:) = x'/norm(x);
end

a = norm(Pw(2,:) - Pw(3,:));
b = norm(Pw(1,:) - Pw(3,:));
c = norm(Pw(1,:) - Pw(2,:));

ca = dot(u(2,:),u(3,:));
cb = dot(u(1,:),u(3,:));
cg = dot(u(1,:),u(2,:));

coeffs = p3p_polynomial(a,b,c,ca,cb,cg);
xs = roots(coeffs);

bestErr = inf;

for i = 1:length(xs)
    x = xs(i);
    if ~isreal(x) || x<=0, continue; end

    y = (b^2 - a^2*x^2 + 2*a^2*x*ca - a^2) / ...
        (2*(b^2*cb - a^2*x*ca));
    if y<=0, continue; end

    d1 = sqrt(c^2 / (1 + x^2 - 2*x*cg));
    d2 = x*d1;
    d3 = y*d1;

    Pc = [
        d1*u(1,:);
        d2*u(2,:);
        d3*u(3,:);
    ];

    [R,T] = rigid_transform_3D(Pw, Pc);
    err = reprojection_error(Pw, uv, R, T, K);

    if err < bestErr
        bestErr = err;
        bestR = R;
        bestT = T;
    end
end
end

LM 优化的数学核心

位姿参数化（Rodrigues）

cs 复制代码

function x = pose_to_vector(R, T)
r = rotm2axang(R);
x = [r(1:3)*r(4); T];
end

cs 复制代码

function [R,T] = vector_to_pose(x)
theta = norm(x(1:3));
if theta < 1e-12
    R = eye(3);
else
    k = x(1:3)/theta;
    R = axang2rotm([k' theta]);
end
T = x(4:6);
end

LM 残差（重投影误差）

cs 复制代码

function r = reproj_residual(x, Pw, uv, K)

[R,T] = vector_to_pose(x);
N = size(Pw,1);
r = zeros(2*N,1);

for i = 1:N
    Pc = R*Pw(i,:)' + T;
    p = K*(Pc/Pc(3));
    r(2*i-1:2*i) = p(1:2) - uv(i,:)';
end
end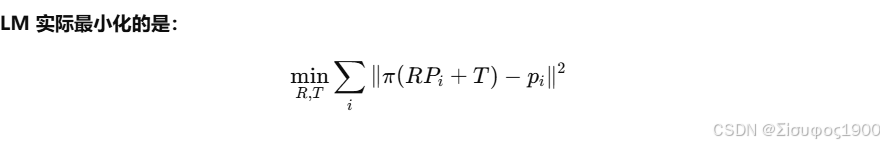

四、常见 PnP 算法名字

P3P（3 点解）
EPnP（高效）
DLT
LM-PnP（优化）
OpenCV：solvePnP
HALCON：find_marks_and_pose