核心概念基础
范式（Normal Form）是关系模式规范化程度的标准。讨论范式前，需明确两个关键概念：
-
函数依赖 ：设R(U)是属性集U上的关系模式，X，Y是U的子集。若对于R(U)的任意一个可能的关系r，r中不可能存在两个元组在X上的属性值相等，而在Y上的属性值不等，则称 "X函数确定Y" 或 "Y函数依赖于X"，记作X→Y。
-
码（键） ：设K为R<U, F>中的属性或属性组合，若U完全函数依赖于K，则K称为R的一个候选码 。若关系模式中有多个候选码，则选定其中一个作为主码 。包含在任何一个候选码中的属性称为主属性 ；不包含在任何候选码中的属性称为非主属性。
-
超码 ：如果U部分依赖 于K，即
，则K称为超码。
范式定义
1. 第一范式（1NF）
-
定义 ：如果一个关系模式R的所有属性都是不可分的基本数据项，则R∈1NF。
-
实质：关系的每一个分量必须是原子的，即不允许表中嵌套表。这是关系数据库模式最基本的要求。
2. 第二范式（2NF）
-
定义 ：若R∈1NF，且每一个非主属性完全函数依赖于任何一个候选码，则R∈2NF。
-
实质 ：消除了非主属性对码的部分函数依赖。如果码是单属性，则1NF自然满足2NF。
3. 第三范式（3NF）
-
定义 ：设关系模式R<U, F>∈1NF，若R中不存在这样的码X、属性组Y以及非主属性Z（Z ⊈ Y），使得X→Y，Y→Z成立，且Y不函数依赖于X，则称R<U, F>∈3NF。
-
等价定义 ：若R∈1NF，且每一个非主属性既不部分依赖于码，也不传递依赖于码，则R∈3NF。
-
实质 ：消除了非主属性对码的传递函数依赖。
4. BC范式（BCNF，Boyce Codd Normal Form）
-
定义 ：设关系模式R<U, F>∈1NF，若对于R中的每一个非平凡的函数依赖X→Y（Y ⊈ X），X都含有码，则R∈BCNF。
-
实质 ：BCNF是修正的第三范式，它要求所有不平凡的函数依赖的决定因素都必须是候选码 。BCNF比3NF更为严格，消除了主属性对非码属性的部分和传递依赖。
-
结论：如果R∈BCNF，则R一定∈3NF；反之则不一定成立。
总结关系
范式级别从低到高为：1NF ⊃ 2NF ⊃ 3NF ⊃ BCNF
规范化过程是通过模式分解，将一个低一级范式的关系模式转换为若干个高一级范式的关系模式的集合，以逐步消除数据依赖中的不合理部分，减少数据冗余和操作异常。
判断给定关系模式最高属于什么范式
假设关系模式R(U,F)已满足第一范式（1NF），即所有属性都是原子的。
1.求候选键
找出 R 的所有候选键（候选码），并区分主属性（包含在任一候选键中的属性）与非主属性。
求候选码的步骤在前面的文章写过，这里不再赘述。
2.判断2NF（ 仅当候选键为复合属性时才需要检查。若候选键为单属性，则自动满足2NF**）**
-
检查部分函数依赖 ：是否存在非主属性对某个候选键的部分函数依赖（即非主属性依赖于候选键的真子集）。
-
结论：如果存在部分依赖，则 R 最高属于1NF；否则，R 至少满足2NF，进入第3步判断。
3.判断3NF
-
检查传递函数依赖 ：是否存在非主属性对候选键的传递函数依赖 。即是否存在候选键 X、属性组 Y 和非主属性 Z（
-
结论：如果存在传递依赖，则 R 最高属于2NF；否则，R 至少满足3NF，进入第4步判断。
4.判断BCNF
-
检查所有函数依赖 ：对于 F 中的每一个非平凡函数依赖 X→Y（
-
结论：如果所有非平凡依赖的决定因素 X 都是超键，则 R 满足BCNF；否则，R 最高属于3NF。
画个程序流程图来描述范式判断过程：
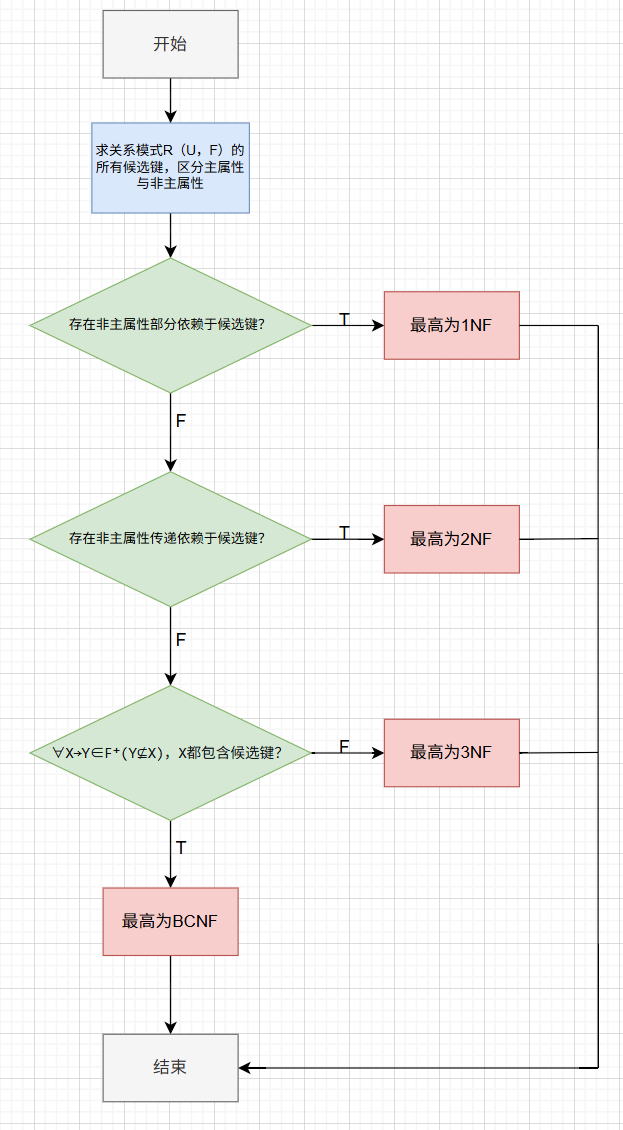
注：流程图中判断BC范式时，理论上应该检查F⁺，但实践中通常只检查F。
习题
#例1
R（U，F），U={A,B,C,D}，F={B→D，D→B，AB→C}。
解：
候选键是AB，AD。
主属性：A，B，D。
非主属性：C。
不存在非主属性部分依赖于候选键，满足2NF。
不存在非主属性对候选键的传递依赖，满足3NF。
并非所有的非平凡依赖的决定因素都是超键（B→D，D→B），违反BCNF。
所以该模式最高属于3NF。
#例2
R（U，F），U={A,B,C}，F={A→B，B→A，A→C}。
解：
候选键是A，B。
主属性：A，B。
非主属性：C。
不存在非主属性部分依赖于候选键，满足2NF。
不存在非主属性对候选键的传递依赖，满足3NF。
所有的非平凡依赖的决定因素都是超键，满足BCNF。
所以该模式最高属于BCNF。