大家好, 我是印刻君. 今天我们来聊 矩阵 (matrix).
矩阵是 AI 背后的数学工具, 图像识别时会用到它, 同类推荐时会用到它, 大模型训练也会用到它. 它让 AI 能够批量处理数据. 如果我们想了解 AI 原理, 了解矩阵很有必要.
这篇文章, 我会以向量为基础, 引出 矩阵 的概念, 介绍矩阵的两种理解方式, 以及最常用的四种核心运算.
不熟悉向量相关概念? 可以看我的文章: 不再费脑,写给 AI 爱好者的向量 (Vector) 入门课
矩阵的两种理解方式
1. 给苹果打分: 矩阵是多个向量的组合
假设你是一家水果店的老板, 想知道一款苹果在大众心中的认可度, 于是你找来了 3 个员工小印, 小刻, 小君, 让他们根据自己的偏好给这款苹果打分 (分数无上限)
每个人的偏好都可以用一个向量表示, 打分过程就是偏好向量与苹果特征向量的计算
-
小印是 "颜值党", 他挑选苹果只看重颜色, 完全不在乎甜不甜、脆不脆, 他的偏好向量是 (10, 0, 0). 打分结果是:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ( 10 × 0.9 ) + ( 0 × 5 ) + ( 0 × 8 ) = 9 (10 \times 0.9) + (0 \times 5) + (0 \times 8) = 9 </math>(10×0.9)+(0×5)+(0×8)=9
-
小刻是 "口味党", 他完全不在乎颜色, 喜欢甜口但讨厌脆感, 他的偏好向量是 (0, 2, -1). 打分结果是:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ( 0 × 0.9 ) + ( 2 × 5 ) + ( − 1 × 8 ) = 2 (0 \times 0.9) + (2 \times 5) + (-1 \times 8) = 2 </math>(0×0.9)+(2×5)+(−1×8)=2
-
小君是 "综合党", 他兼顾颜色, 甜度和脆度, 他的偏好向量是 (1, 1, 1). 打分解果是:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ( 1 × 0.9 ) + ( 1 × 5 ) + ( 1 × 8 ) = 13.9 (1 \times 0.9 ) + (1 \times 5) + (1 \times 8) = 13.9 </math>(1×0.9)+(1×5)+(1×8)=13.9
为了简化记录, 我们可以把3位员工的偏好向量 "一排排叠起来" 组成一个矩阵 A, 把苹果的特征向量 "竖起来" 写成向量 x, 最终的打分结果也竖起来写成向量 b. 这样就有了下面的式子:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> [ 10 0 0 0 2 − 1 1 1 1 ] ⋅ [ 0.9 5 8 ] = [ 9 2 13.9 ] \begin{bmatrix} 10 & 0 & 0 \\ 0 & 2 & -1 \\ 1 & 1 & 1 \end{bmatrix}\cdot\begin{bmatrix} 0.9 \\ 5 \\ 8\end{bmatrix}=\begin{bmatrix} 9 \\ 2 \\ 13.9 \end{bmatrix} </math> 10010210−11 ⋅ 0.958 = 9213.9
简写为
<math xmlns="http://www.w3.org/1998/Math/MathML"> A x = b A x = b </math>Ax=b
这就是矩阵的第一种理解: 矩阵是多个向量的组合。它能帮我们一次性完成多组规则相同的计算, 不用逐个单独运算.
2. 反推苹果特征: 矩阵是方程组的系数
同样以水果店为例,这次我们换个场景: 你不知道苹果的具体特征(颜色、甜度、脆度都是未知的),但你手头有 3 位员工的打分结果,以及他们的评分标准. 现在你想反推这个苹果的具体特征, 应该怎么办呢?
我们假设颜色、甜度、脆度为 x1, x2, x3, 根据之前评分规则, 就可以列出一组方程:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> { 10 x 1 + 0 x 2 + 0 x 3 = 9 0 x 1 + 2 x 2 − 1 x 3 = 2 1 x 1 + 1 x 2 + 1 x 3 = 13.9 \begin{cases} 10x_1 + 0x_2 + 0x_3 &= 9 \\ 0x_1 + 2x_2 - 1x_3 &= 2 \\ 1x_1 + 1x_2 + 1x_3 &= 13.9 \end{cases} </math>⎩ ⎨ ⎧10x1+0x2+0x30x1+2x2−1x31x1+1x2+1x3=9=2=13.9
不难发现, 如果我们把 x1, x2, x3 的前面的系数提取出来, 它恰好就是一个矩阵:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> [ 10 0 0 0 2 − 1 1 1 1 ] \begin{bmatrix} 10 & 0 & 0 \\ 0 & 2 & -1 \\ 1 & 1 & 1 \end{bmatrix} </math> 10010210−11
因此, 上面的方程组可以简写为矩阵形式:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> [ 10 0 0 0 2 − 1 1 1 1 ] ⋅ [ x 1 x 2 x 3 ] = [ 9 2 13.9 ] \begin{bmatrix} 10 & 0 & 0 \\ 0 & 2 & -1 \\ 1 & 1 & 1 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}=\begin{bmatrix} 9 \\ 2 \\ 13.9 \end{bmatrix} </math> 10010210−11 ⋅ x1x2x3 = 9213.9
只要解这个矩阵方程, 我们就可以算出苹果的特征向量. 这就是矩阵的第二种核心理解:矩阵是线性方程组的系数集合。
矩阵的四种核心运算
理解了矩阵是什么之后, 我们再来看它的四种核心运算. 这里不深入讲解复杂的运算性质, 重点讲清基础规则, 再结合AI领域的实际场景, 说说每种运算的用途.
1. 矩阵的加法/减法
运算性质
矩阵的加法和减法有个前提: 两个矩阵必须形状相同 (也就是行数和列数都完全一致), 否则无法计算.
计算方法很简单: 把两个矩阵对应位置的元素直接相加或相减即可.
举个例子,现有两个 2×2 的矩阵 A 和 B:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> A = [ 1 2 3 4 ] B = [ 5 6 7 8 ] A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \quad B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} </math>A=[1324]B=[5768]
矩阵加法 A + B:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> [ 1 + 5 2 + 6 3 + 7 4 + 8 ] = [ 6 8 10 12 ] \begin{bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \end{bmatrix}= \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix} </math>[1+53+72+64+8]=[610812]
矩阵减法: A - B:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> [ 1 − 5 2 − 6 3 − 7 4 − 8 ] = [ − 4 − 4 − 4 − 4 ] \begin{bmatrix} 1 - 5 & 2 - 6 \\ 3 - 7 & 4 - 8 \end{bmatrix}= \begin{bmatrix} -4 & -4 \\ -4 & -4 \end{bmatrix} </math>[1−53−72−64−8]=[−4−4−4−4]
AI 领域的应用例子
下面我们各举一下加法和减法在 AI 应用场景中的例子, 帮助你理解矩阵加法和减法的实际价值:
加法例子: 大模型的位置编码
大模型的 Transformer 架构中, Token 是被并行处理的, 本身没有位置信息, 比如它分不清 "我爱吃苹果" 和 "苹果爱吃我".
不熟悉 Transformer 架构, 可以看我的文章: 数学不好也能懂: 解读 AI 经典论文《Attention is All You Need》与大模型生成原理
为了解决这个问题, 我们需要给每个词向量增加位置信息.
按照我们之前说的 矩阵是向量的组合, Transfromer 会先把词向量组合成一个 "词向量矩阵", 再生成一个记录位置信息的 "位置向量矩阵". 通过矩阵加法, 模型就能同时获取 "每个 Token 的含义" 和 "每个词的位置" 两个关键信息.
减法例子: 监控中的运动检测
我们先补充一点图像知识: 如果是黑白监控, 一帧画面里的每个像素点都能转换成一个亮度数值:
- 0 = 纯黑
- 255 = 纯白
- 128 = 灰色
这样一来, 一帧画面就可以看成一个 "像素矩阵".
运动检测的核心逻辑很简单: 先把没有物体移动的 "背景画面" 转换成 "背景矩阵", 再用实时的 "当前画面矩阵" 减去 "背景矩阵". 如果结果矩阵里的数值几乎都是 0, 说明画面静止; 如果某一块区域有明显数值, 就说明这块区域有物体在移动. 这就是最基础的运动检测算法
2. 矩阵的乘法
运算性质
矩阵乘法的规则比加减复杂一点, 首先要满足一个前提: 第一个矩阵的列数, 必须等于第二个矩阵的行数, 否则无法计算.
它的计算方式是, 第一个矩阵的每一行的元素, 去和第二个矩阵的每一列的元素对应位置的元素相乘后, 再把所有的乘积加起来
听起来有点难懂, 我们举个例子, 假如有个 2 * 3 和 3 * 2 的矩阵 A 和 B
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> A = [ 1 2 3 4 5 6 ] B = [ 1 2 3 4 5 6 ] A = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \end{bmatrix} \quad B = \begin{bmatrix} 1 & 2\\ 3 & 4\\ 5 & 6 \end{bmatrix} </math>A=[142536]B= 135246
二者相乘
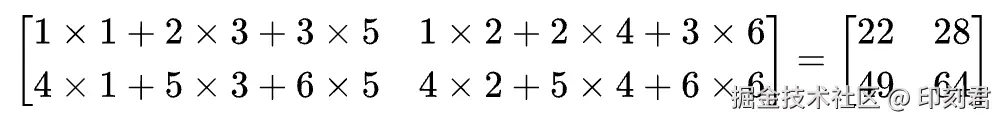
-
我们先拿 A 的第一行和 B 的第一列对应相乘再相加
<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 × 1 + 2 × 3 + 3 × 5 = 22 1 \times 1 + 2 \times 3 + 3 \times 5 = 22 </math>1×1+2×3+3×5=22
-
再拿 A 的第一行和 B 的第一列对应相乘再相加
<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 × 2 + 2 × 4 + 3 × 6 = 28 1 \times 2 + 2 \times 4 + 3 \times 6 = 28 </math>1×2+2×4+3×6=28
-
再拿 A 的第二行和 B 的第一列对应相乘再相加
<math xmlns="http://www.w3.org/1998/Math/MathML"> 4 × 1 + 5 × 3 + 6 × 5 = 49 4 \times 1 + 5 \times 3 + 6 \times 5 = 49 </math>4×1+5×3+6×5=49
-
最后拿 A 的第二行和 B 的第二列对应相乘再相加
<math xmlns="http://www.w3.org/1998/Math/MathML"> 4 × 2 + 5 × 4 + 6 × 6 = 64 4 \times 2 + 5 \times 4 + 6 \times 6 = 64 </math>4×2+5×4+6×6=64
AI 应用例子
矩阵乘法在推荐系统中用得很多, 比如视频 APP, 购物平台的 "猜你喜欢" 功能.
我们以推荐电影为例:
- 构建一个用户矩阵 U: 每一行代表一个用户, 每一列代表一个用户特征 (比如 "喜欢科幻", "喜欢恐怖" 等);
- 构建一个电影矩阵 M: 每一行代表一个电影特征 (和用户特征对应, 比如 "科幻程度", "恐怖程度" 等). 每一列代表一部电影;
- 把用户矩阵 U 和电影矩阵 M 相乘, 得到一个 "兴趣矩阵 R". R里的每个数值, 都代表某个用户对某部电影的感兴趣程度. 数值越大, 越可能喜欢; 数值越小, 越不感兴趣.
其实这个过程的本质, 就是用矩阵乘法计算 "用户向量" 和 "电影向量" 的相似度.
整个矩阵运算过程, 就是从用户矩阵中取出一行行的用户向量 u 去和电影向量 m 相乘:
向量的乘法公式是:
<math xmlns="http://www.w3.org/1998/Math/MathML"> u ⃗ ⋅ v ⃗ = ∣ u ⃗ ∣ × ∣ m ⃗ ∣ × c o s ( θ ) \vec{u} \cdot \vec{v} = |\vec{u}| \times |\vec{m}| \times cos(\theta) </math>u ⋅v =∣u ∣×∣m ∣×cos(θ)
其中 cos(θ) 是余弦相似度, 用来判断两个向量是否相似
如果我们把向量 u 和向量 m 都进行归一化处理, 也就是让它们都长度都为 1, 那么结果就变成了
<math xmlns="http://www.w3.org/1998/Math/MathML"> u ⃗ ⋅ m ⃗ = c o s ( θ ) \vec{u} \cdot \vec{m} = cos(\theta) </math>u ⋅m =cos(θ)
所以矩阵的乘法, 本质上就是批量计算多个向量之间的相似度.
3. 矩阵的转置
运算性质
矩阵的转置很简单, 就是把矩阵沿着对角线 (从左上到右下) 进行翻转, 通常写作 AT 或者 A′
简单来说, 就是把矩阵的行写成列, 把列写成行
举个例子:
假设有一个 2 行 3 列的矩阵 A:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> A = [ 1 2 3 4 5 6 ] A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix} </math>A=[142536]
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> A T = [ 1 4 2 5 3 6 ] A^T = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \\ \end{bmatrix} </math>AT= 123456
AI 应用例子
转置在 AI 中的核心作用, 是解决"矩阵形状不匹配"的问题. 我们之前说过, 矩阵乘法有个前提: 第一个矩阵的列数要等于第二个矩阵的行数.
在神经网络计算中, 经常会遇到两个矩阵包含有用数据, 但形状对不上, 无法直接相乘的情况. 这时候就可以用转置调整其中一个矩阵的行数和列数, 让它们满足乘法条件.
转置就像一个 "适配器", 帮两个矩阵顺利完成后续计算.
4. 矩阵的哈达玛积
运算性质
需要注意, 哈达玛积的计算规则, 和我们之前说的矩阵乘法完全不同, 它要求两个矩阵的形状完全一致, 也就是行数和列数相同. 它的计算方法是对应位置的元素直接相乘, 结果矩阵的形状和原来保持一致.
哈达玛积通常写作:
<math xmlns="http://www.w3.org/1998/Math/MathML"> A ⊙ B A \odot B </math>A⊙B
举个例子, 假设有两个 2 行 2 列的矩阵 A 和 B:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> A = [ 1 2 3 4 ] B = [ 5 6 7 8 ] A = \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix} \quad B = \begin{bmatrix} 5 & 6\\ 7 & 8 \end{bmatrix} </math>A=[1324]B=[5768]
它们的哈达玛积为:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> [ 1 × 5 2 × 6 3 × 7 4 × 8 ] = [ 5 12 21 32 ] \begin{bmatrix} 1 \times 5 & 2 \times 6 \\ 3 \times 7 & 4 \times 8 \end{bmatrix} = \begin{bmatrix} 5 & 12 \\ 21 & 32 \end{bmatrix} </math>[1×53×72×64×8]=[5211232]
AI 应用例子
哈达玛积的核心用途是 "筛选有效信息, 屏蔽无效信息", 最典型的场景是 Transformer 的掩码机制和图像处理的抠图.
Transformer 的掩码机制
Transformer 处理文本时, 为了防止 Transformer "偷看" 后面还没处理的词语, 需要用到 "掩码".
掩码的一种方法, 就是会生成一个由 0 和 1 的 "掩码矩阵", 再与输入特征进行哈达玛积, 结果矩阵中, 0 对应的位置会被屏蔽, 1 对应的位置保留原始信息, 从而实现 "不偷看" 的效果.
图像处理中的抠图
如果我们想把一个图像中的人像抠出来, 可以先做一个 "掩膜矩阵": 它的人像区域数值全是 1, 其余背景部分数值全部是 0
把图片对应的像素矩阵和掩膜矩阵做哈达玛积, 最终得到的矩阵就只保留了人像. 这就是最基础的抠图逻辑.
总结
总结一下, 本文我们核心介绍了矩阵的两个核心理解和四种核心运算:
-
矩阵的两个核心理解: a. 多个向量的组合; b. 线性方程组的系数集合;
-
矩阵的四种核心运算: a. 加/减法 (形状相同, 对应元素运算); b. 乘法 (批量计算向量相似度); c. 转置 (调整形状, 适配运算); d. 哈达玛积 (筛选信息, 屏蔽无效内容).
这些运算看似基础, 却是 AI 领域 (比如大模型, 推荐系统, 图像处理) 的核心数学工具, 理解它们的逻辑, 能帮我们更好地看懂AI技术的底层原理.
我是印刻君, 一位探索 AI 的前端程序员, 关注我, 让 AI 知识有温度, 技术落地有深度.