面试题：推导一下softmax中为啥要除以根号d

我整理好的1000+面试题，请看
大模型面试题总结-CSDN博客

或者

https://gitee.com/lilitom/ai_interview_questions/blob/master/README.md

最好将URL复制到浏览器中打开，不然可能无法直接打开

好了，我们今天针对上面的问题，

推导一下softmax中为啥要除以根号d

先看下具体的详细推导，文末有代码来可视化的证明。

1. 定义与假设 这里我们需要事先做一个假设：
和是两个独立的随机矩阵，维度均为。
每个元素和是独立同分布（i.i.d.）的随机变量，满足：
- 均值，
- 方差。

计算的任意一个元素 =。

2. 计算均值 由于和独立且均值为 0：

3. 计算方差 方差定义为：

由于，第二项为 0，因此：

展开平方项：

因此：

由于和独立：

对于交叉项：

因为和独立（），且，同理。
对于平方项：

综上：

4. 缩放因子的作用 为了控制方差，使的方差为 1（便于 Softmax 计算和梯度稳定），我们对其除以：

此时，方差变为：

5. 直观解释
未缩放时：的方差随线性增长，导致 Softmax 输入值过大，输出接近 one-hot 分布，梯度消失。
缩放后：方差稳定为 1，Softmax 输入分布更平滑，梯度传播更稳定。

让LLM写了一段代码

复制代码

import numpy as np
import matplotlib.pyplot as plt

def verify_scaled_dot_product_variance(d_k=64, num_samples=10000):
    """
    验证缩放点积注意力中QK^T的方差计算
    参数:
        d_k: 键/查询向量的维度
        num_samples: 采样次数
    """
    # 存储未缩放和缩放后的方差结果
    variances_unscaled = []
    variances_scaled = []
    
    for _ in range(num_samples):
        # 生成随机矩阵Q和K (元素服从标准正态分布 N(0,1))
        Q = np.random.randn(1, d_k)  # 1 x d_k
        K = np.random.randn(1, d_k)  # 1 x d_k
        
        # 计算点积 QK^T (这里Q和K都是单行向量，点积即内积)
        dot_product = np.dot(Q, K.T)[0, 0]  # 提取标量值
        
        # 缩放后的点积
        scaled_dot_product = dot_product / np.sqrt(d_k)
        
        variances_unscaled.append(dot_product ** 2)  # 因为E[QK^T]=0，方差=E[(QK^T)^2]
        variances_scaled.append(scaled_dot_product ** 2)
    
    # 转换为numpy数组
    variances_unscaled = np.array(variances_unscaled)
    variances_scaled = np.array(variances_scaled)
    
    # 计算统计方差
    empirical_var_unscaled = np.mean(variances_unscaled)
    empirical_var_scaled = np.mean(variances_scaled)
    
    # 理论值
    theoretical_var_unscaled = d_k
    theoretical_var_scaled = 1.0
    
    print(f"理论方差 (未缩放): {theoretical_var_unscaled:.2f}")
    print(f"实际方差 (未缩放): {empirical_var_unscaled:.2f}")
    print(f"理论方差 (缩放后): {theoretical_var_scaled:.2f}")
    print(f"实际方差 (缩放后): {empirical_var_scaled:.2f}")
    
    # 绘制结果
    plt.figure(figsize=(10, 5))
    plt.subplot(1, 2, 1)
    plt.hist(variances_unscaled, bins=50, alpha=0.7)
    plt.axvline(theoretical_var_unscaled, color='r', linestyle='--', label='理论方差')
    plt.title(f"未缩放点积方差 (d_k={d_k})")
    plt.xlabel("方差")
    plt.ylabel("频次")
    plt.legend()
    
    plt.subplot(1, 2, 2)
    plt.hist(variances_scaled, bins=50, alpha=0.7, color='orange')
    plt.axvline(theoretical_var_scaled, color='r', linestyle='--', label='理论方差')
    plt.title(f"缩放后点积方差 (除以√{d_k})")
    plt.xlabel("方差")
    plt.legend()
    
    plt.tight_layout()
    plt.show()

# 运行验证 (默认d_k=64)
verify_scaled_dot_product_variance()

# 测试不同d_k值的影响
for d_k in [16, 64, 256]:
    print(f"\n验证 d_k = {d_k}:")
    verify_scaled_dot_product_variance(d_k=d_k, num_samples=10000)

运行结果如下：

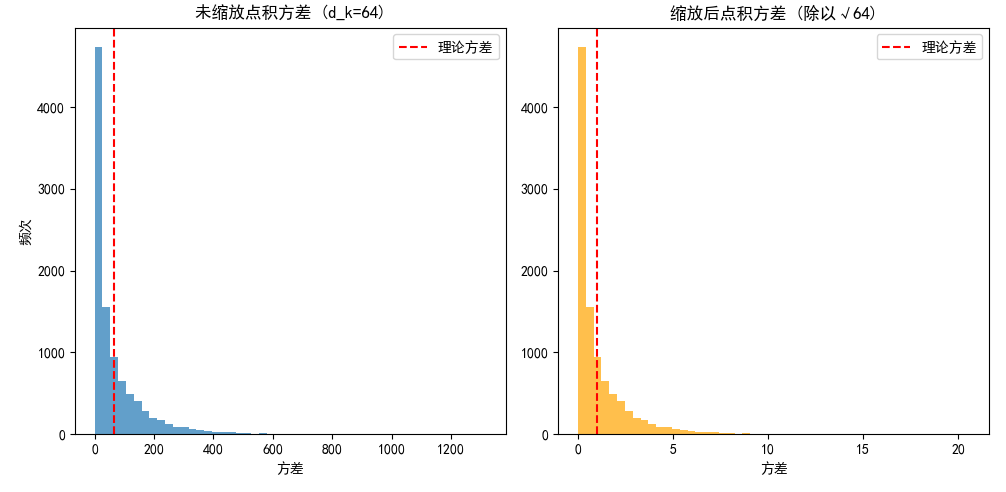
看到没，哥哥