马尔可夫跳变系统（Markovian Jump Systems, MJS）是一类具有随机切换特性的动态系统，其模态切换由马尔可夫过程描述。镇定此类系统的核心是通过控制器设计，确保系统在随机切换下保持稳定。
一、系统模型
对于固定于概率空间中的马尔可夫跳变系统，可以表示为：
其中，为系统状态，
是控制信号，
为系统模态，
为模态依赖的系统矩阵。
系统模态由马尔可夫过程
所确定，其对应的转移概率矩阵可概括为：
其中，与
等价均是系统模态，
是一个无穷小时间且满足
。
是马尔可夫过程中从模态
跳变至
的转移速率，其满足
且
。
通常，最简单的控制器是根据线性反馈设置控制率：
其中，为控制器增益。
因此，闭环系统方程化简为：
二、控制增益求解
可以利用李雅普诺夫第二法求解控制器增益。
构造模态依赖的李雅普诺夫函数：
其中为某一待定的正定矩阵，
。接下来需求得合适控制器增益
使得李雅普诺夫函数
的导数小于0，这样可以判定系统具有李雅普诺夫稳定。但是我们所研究的马尔可夫跳变系统是随机系统，不具备确定系统的随机稳定性概念，因此借用随机稳定的概念使系统镇定，即
也就是在数学期望范围内满足李雅普诺夫稳定性就行了。
简单求导，我们可以得到：
要使得，需保证
注意到上述不等式方程中有些项同时存在和
，这无法利用LMI直接求解，因此需要将上述不等式等价变换，两边同时前后同乘
借以消除。但注意到，
在前后同乘
会变复杂，因此需要优先对
进行处理。注意到，
根据舒尔补不等式引理，上述不等式等价于
为了便于书写和计算，定义，上式等价于
再定义，
，上述等式前后同乘正定矩阵
和
，不等式性质不变，可得
注意到正定矩阵满足
，上式可重写为
上述不等式可以用LMI直接求解和
，控制增益由下式直接求得
三、仿真测试
用最简单的参数测试一下。假设该马尔可夫跳变系统仅具有2个模态，各模态参数设置如下：
模态1：
模态2：
不难发现，这两个系统都是不完全可控的。但是，模态1是不可镇定的，不能够通过LMI求解出控制增益。而模态2是可镇定的，可以得到
。
在无控制器下，各模态在初始状态为时，其系统状态响应曲线如下图所示。
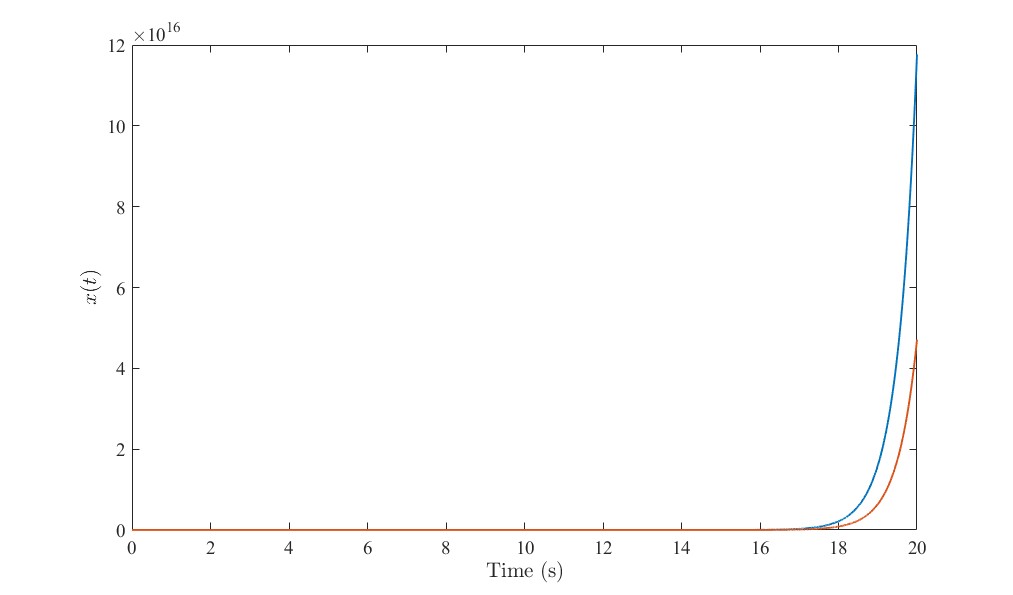模态1状态下的系统
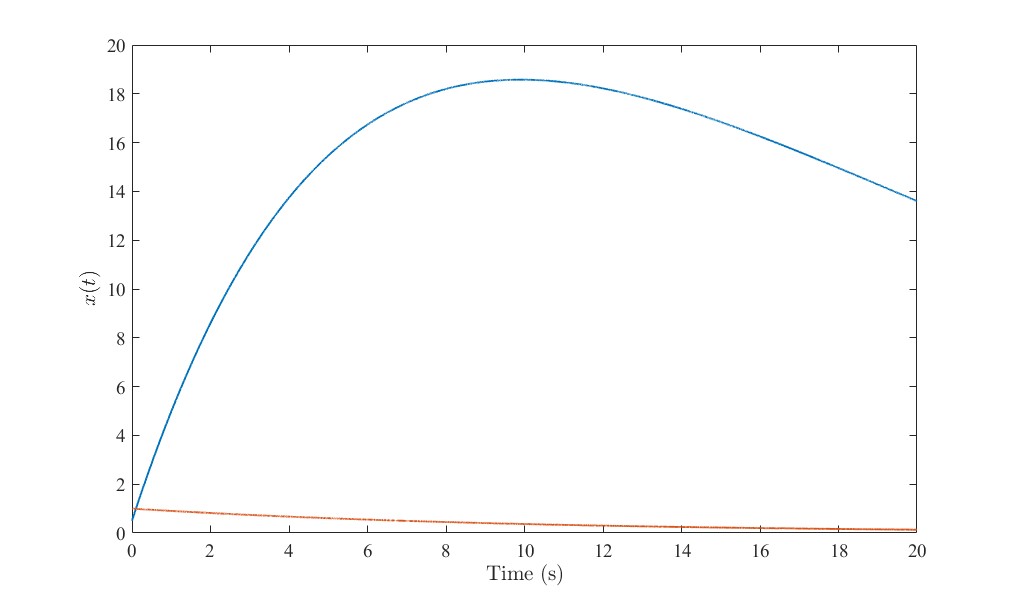模态2状态下的系统
可以看到，模态1状态下的开环系统是发散的，模态2状态下的开环系统有收敛的趋势，但极其缓慢。这二者都需要设计控制器使其镇定。
如果仅对单一模态分别设计状态反馈控制器，利用MATLAB求解LMI得到控制增益：
对于模态1，因为系统无法镇定且不完全可控，所以求解不出控制增益。
对于模态2，
仅对模态系统1用状态反馈控制是失败的。如果仅是对单一模态2下的子系统在同样初始状态下进行控制，我们通过SIMULINK进行仿真，可得
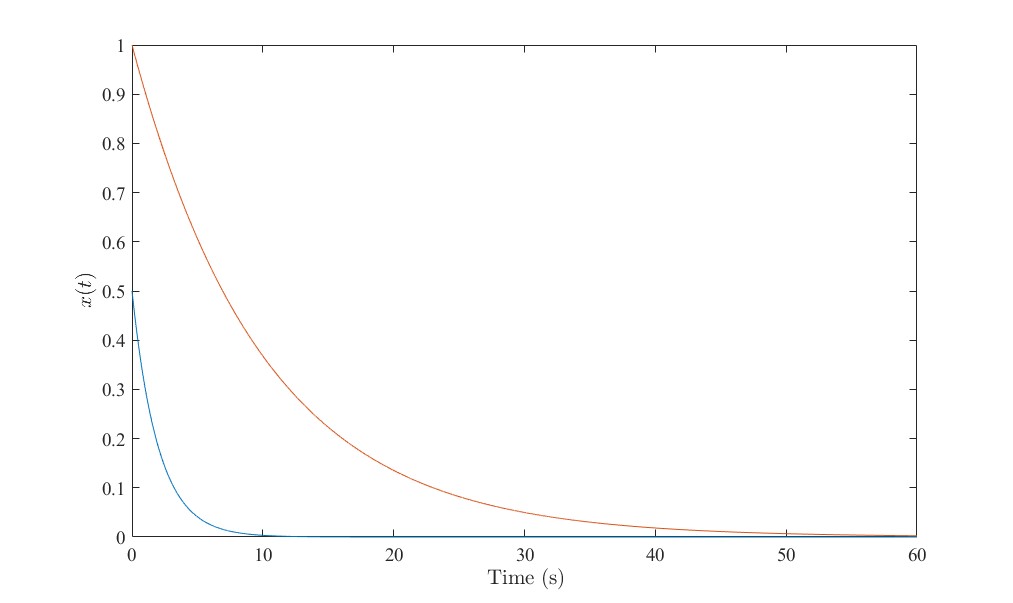模态2下的闭环系统响应曲线
可以看到，按照传统的控制器设计方法开环系统2在控制器的作用下能逐渐收敛镇定，但是系统1却求不出控制器增益没有相应控制方式。
但是如果是切换系统，系统在这两个模态中来回切换，则有可能实现镇定。
首先假设假设连续系统马尔可夫过程转移速率矩阵如下：
这是一种慢切换的方式，跃迁速率都很低，模态切换很慢。模态1的控制器无解问题对切换系统的影响很大，此时通过LMI无法得到控制器的解。
系统模态一种可能的模态切换如下图所示。
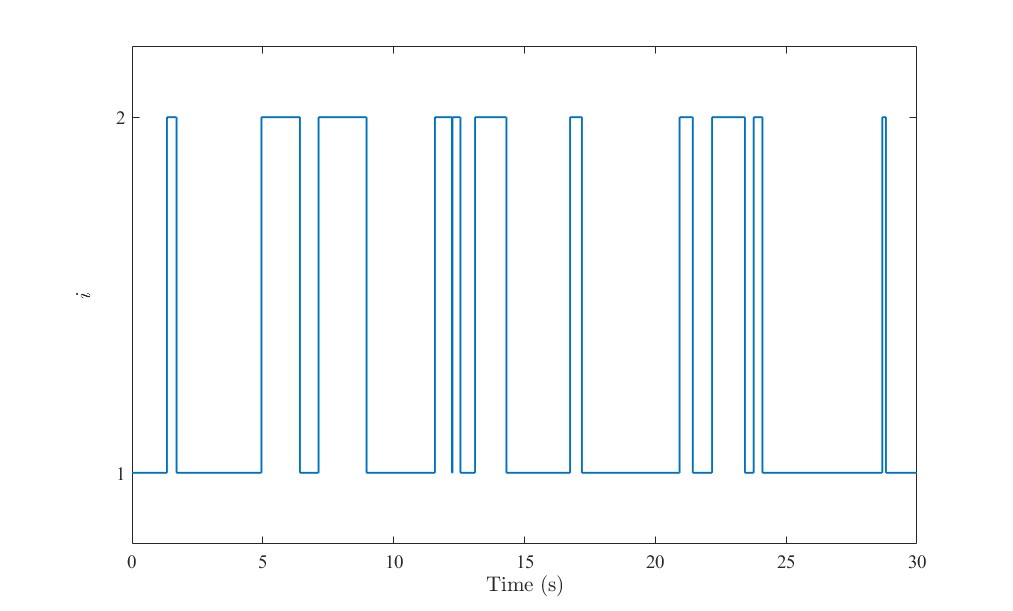[-0.5 0.5; 1 -1]下的系统模态变化
可以看到，系统倾向于呆在模态1下。因为从2跃迁到1快，而从1跃迁到2慢。
注意到，模态1的平均驻留时间为，模态2的平均驻留时间为
。
系统响应曲线如下图所示。
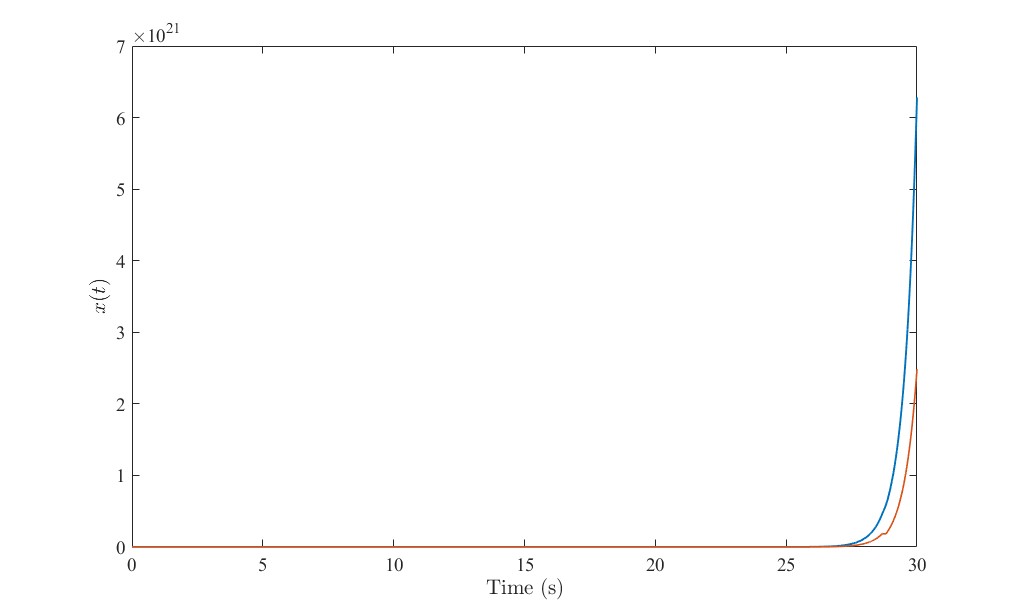开环切换系统响应曲线
可以看到，该系统在模态切换间发散的更快了。
如果将系统转移速率增大，则系统将在模态1不稳定状态下驻留时间更短，系统便有可能能够镇定。假设连续系统马尔可夫过程转移速率矩阵如下：
此时模态1的平均驻留时间为，模态2的平均驻留时间为
，确实切换更频繁了，而且模态更倾向于保留在模态2上。
通过SIMULINK可以得到系统的模态变化，可以验证上述结论。
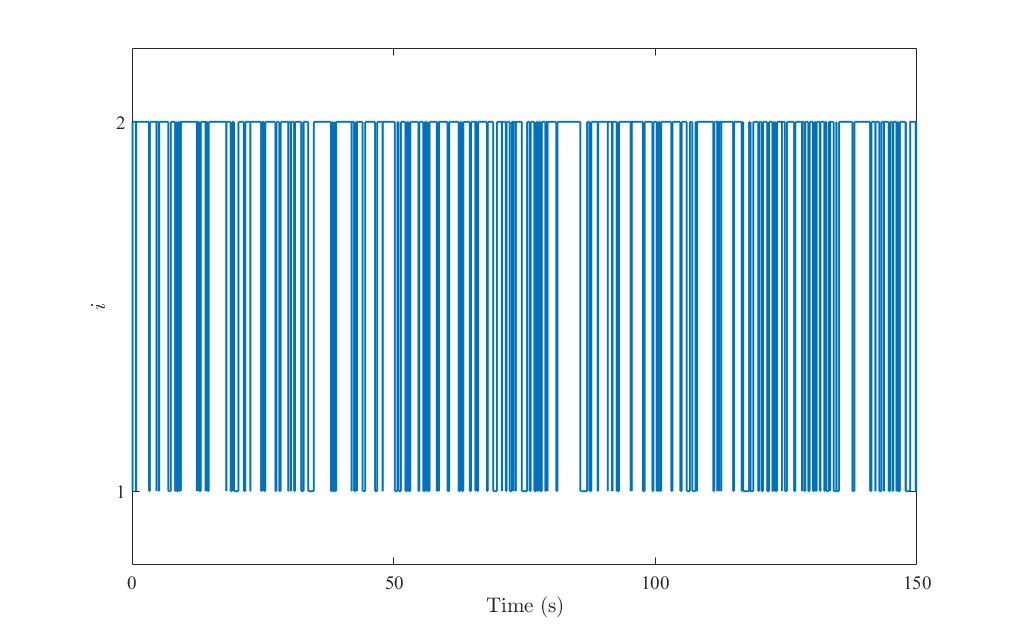[-5 5; 1 -1]下的系统模态变化
开环系统同样可仿真得出切换开环系统的响应曲线：
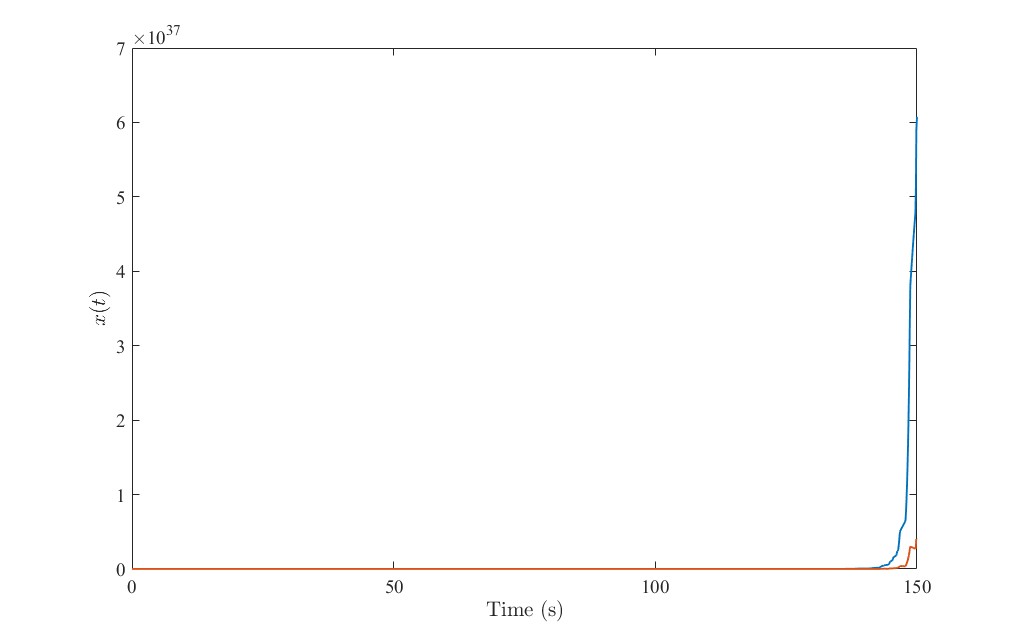[-5 5; 1 -1]下的开环切换系统响应曲线
可以发现，由于系统在不稳定的模态1下运行的时间减少，其发散速度有所减缓，但是系统仍旧是发散的，需要用LMI设计控制器来镇定。
根据转移速率矩阵信息，通过LMI求解可得切换系统模态依赖的控制器增益为：
放入反馈控制器中在SIMULINK中仿真可以得到闭环系统的响应曲线：
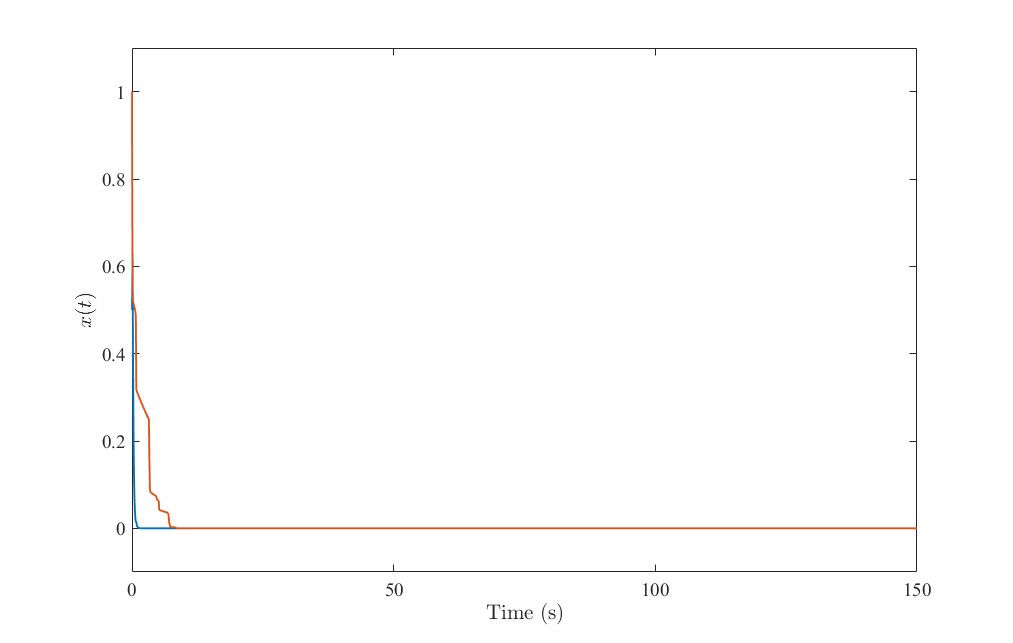[-5 5; 1 -1]下的闭环切换系统响应曲线
可以看到，系统在短时间内很好地镇定了。
与之对比，如果不考虑转移概率信息，可以通过LMI求得模态2下的控制器增益，但是模态1下的控制器增益是无解的。也就是说，我们只能对模态1下的系统不设控制器，或者用模态2的控制器。
（1）如果不设置控制器，那么，
，可以得到
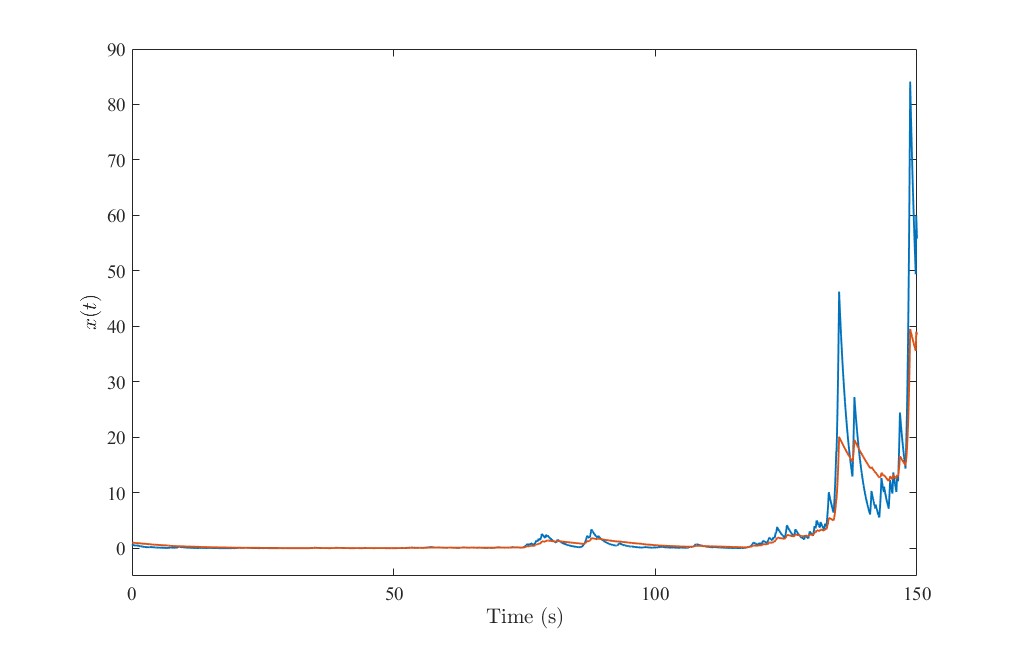模态1不设控制增益的闭环系统响应曲线
（2）如果沿用模态2的控制器给模态1，则，可以得到
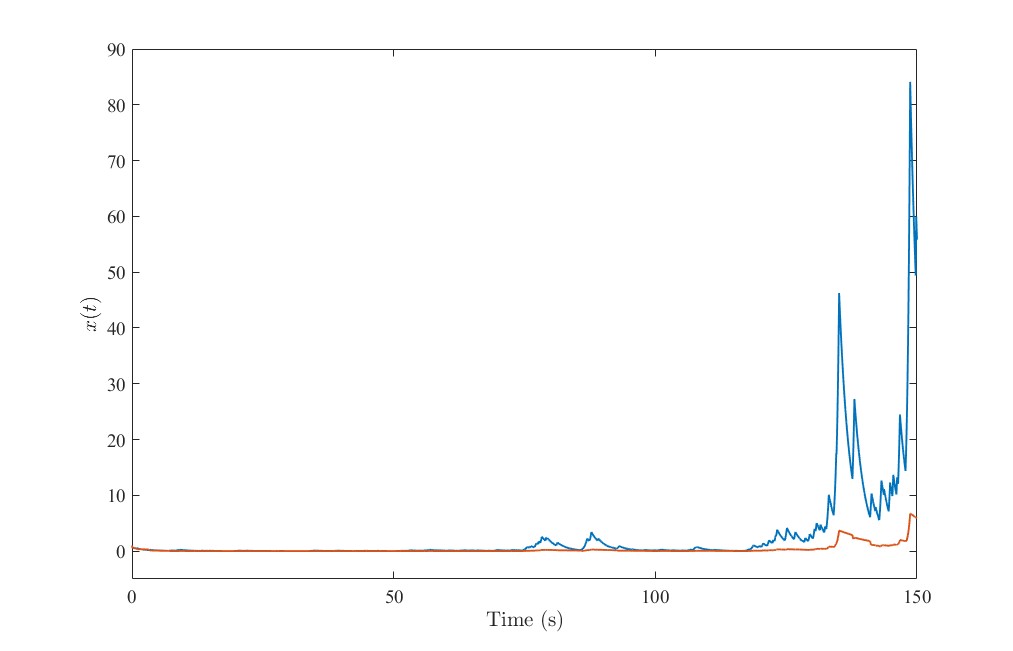模态1借用模态2的控制增益的闭环系统响应曲线
可以看到，上述两种情况下的闭环系统都未收敛。当然这仅是某一种可能模态下系统是发散的，在其它切换规律性这两种控制方法均无法有效镇定系统，而利用转移速率来进行控制器设计的控制策略可以实现系统镇定。
四、结论
利用转移速率矩阵信息进行控制设计，该方法的优势并非总表现为"镇定速度更快"或"超调更小"，而主要体现在保守性和理论保证上。
-
充分利用系统信息，降低保守性
后两种控制方法考虑的是系统"最坏情况"设计。它必须保证在任何可能的切换序列下（哪怕是最恶劣的、导致抖振的切换）系统都稳定。这种要求非常苛刻，导致其设计结果通常非常保守。控制器增益 Ki可能会"过度设计"，以抵御不存在的恶意切换。而本文研究的控制策略利用了切换的统计规律（转移速率）。它知道某些切换频繁，某些罕见，某些甚至不可能（λij=0）。它允许在切换瞬间存在短暂的"能量"上升（李雅普诺夫函数不要求单调递减，只要求其数学期望递减）。这极大地降低了设计的保守性，求得的 Ki是专门为这个特定切换过程"量身定制"的，理论上更"精准"。
-
严格应对切换的随机性
后两种控制方法设计出的控制器，在确定性切换下可能工作良好，但无法从理论上保证在随机切换下的稳定性。当切换由马尔可夫链驱动时，其稳定性需要更严格的条件（随机稳定性）。而本文研究的控制策略的LMI条件直接保证了马尔可夫跳变系统的随机稳定性。这是一个更强的、与模型匹配的理论保证。注意到本文所提出的问题，假如一种模态无法求解控制增益，传统的控制策略必然失效，那么试试本文所提出的切换系统控制求解方式未尝不是一种可能的解决方案。
从现代工业角度上看，马尔可夫跳变系统在工程领域的应用核心在于处理其固有的多模态与随机切换特性。该方法将系统连续运行中离散的状态变化------如双足机器人的步态相位切换、抓取操作中的接触状态转移、多机编队的拓扑重构或环境交互中的地形属性突变------建模为受马尔可夫链驱动的模态跳变过程。相较于独立设计各模态控制器，该方法通过嵌入描述切换规律的转移概率矩阵，实现了多控制器的协同优化设计。这使得系统不仅能保证在任意随机切换序列下的稳定性，更能显著降低传统鲁棒控制的保守性，从而在复杂环境和复杂任务下，实现更优的统计性能指标，如更低的平均能耗、更快的平均任务完成时间或更小的跟踪误差方差。
