复杂表达式的三角平方和化简及其几何意义

在数学和工程问题中，我们常常遇到包含多个三角函数项的复杂表达式。对这些表达式进行化简，将其转化为更简洁的形式，不仅有助于进一步分析，也能揭示隐藏的数学结构。本文考虑一个具体的例子：计算如下平方根表达式

(−ax+rtcos⁡θe)2+(rtθesin⁡λcot⁡β+rt(−sin⁡2λcos⁡λ+1cos⁡λ)sin⁡θe+aysin⁡2λ−ay−azsin⁡λcos⁡λcos⁡λ)2. \sqrt{ (-a_x + r_t \cos\theta_e)^2 + \left( r_t \theta_e \sin\lambda \cot\beta + r_t \left(-\frac{\sin^2\lambda}{\cos\lambda} + \frac{1}{\cos\lambda}\right) \sin\theta_e + \frac{a_y \sin^2\lambda - a_y - a_z \sin\lambda \cos\lambda}{\cos\lambda} \right)^2 }. (−ax+rtcosθe)2+(rtθesinλcotβ+rt(−cosλsin2λ+cosλ1)sinθe+cosλaysin2λ−ay−azsinλcosλ)2 .

我们的目标是将平方根内的部分化为标准形式 (a1sin⁡λ+b1cos⁡λ)2+c12(a_1 \sin\lambda + b_1 \cos\lambda)^2 + c_1^2(a1sinλ+b1cosλ)2+c12，并确定系数 a1a_1a1、b1b_1b1 和 c1c_1c1。这种形式在优化和几何解释中往往更有用，因为它将变量 λ\lambdaλ 的影响分离为一个线性组合的平方加上一个常数项。

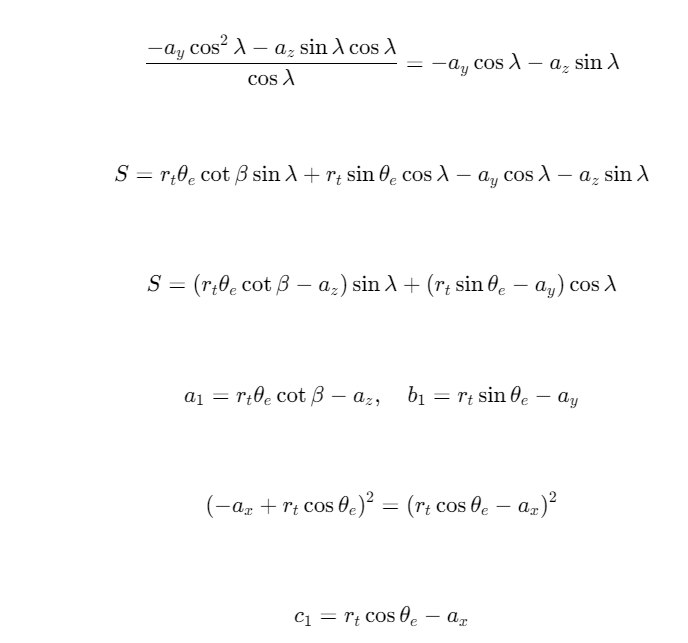
首先，注意到平方根内是两项平方和。第一项 (−ax+rtcos⁡θe)2(-a_x + r_t \cos\theta_e)^2(−ax+rtcosθe)2 不依赖于变量 λ\lambdaλ，我们将其记为 c12c_1^2c12，其中 c1=rtcos⁡θe−axc_1 = r_t \cos\theta_e - a_xc1=rtcosθe−ax。第二项是一个较复杂的表达式，记为 S2S^2S2，其中 SSS 为括号内的部分。我们重点化简 SSS。

观察 SSS 的构成，它包含三项。将第二项中的分式合并：

−sin⁡2λcos⁡λ+1cos⁡λ=1−sin⁡2λcos⁡λ=cos⁡2λcos⁡λ=cos⁡λ. -\frac{\sin^2\lambda}{\cos\lambda} + \frac{1}{\cos\lambda} = \frac{1 - \sin^2\lambda}{\cos\lambda} = \frac{\cos^2\lambda}{\cos\lambda} = \cos\lambda. −cosλsin2λ+cosλ1=cosλ1−sin2λ=cosλcos2λ=cosλ.

于是，SSS 可重写为

S=rtθesin⁡λcot⁡β+rtcos⁡λsin⁡θe+aysin⁡2λ−ay−azsin⁡λcos⁡λcos⁡λ. S = r_t \theta_e \sin\lambda \cot\beta + r_t \cos\lambda \sin\theta_e + \frac{a_y \sin^2\lambda - a_y - a_z \sin\lambda \cos\lambda}{\cos\lambda}. S=rtθesinλcotβ+rtcosλsinθe+cosλaysin2λ−ay−azsinλcosλ.

接下来，处理第三项的分式。将其拆分为两项之和：

aysin⁡2λ−ay−azsin⁡λcos⁡λcos⁡λ=ay(sin⁡2λ−1)cos⁡λ−azsin⁡λ. \frac{a_y \sin^2\lambda - a_y - a_z \sin\lambda \cos\lambda}{\cos\lambda} = \frac{a_y (\sin^2\lambda - 1)}{\cos\lambda} - a_z \sin\lambda. cosλaysin2λ−ay−azsinλcosλ=cosλay(sin2λ−1)−azsinλ.

利用三角恒等式 sin⁡2λ−1=−cos⁡2λ\sin^2\lambda - 1 = -\cos^2\lambdasin2λ−1=−cos2λ，则

ay(sin⁡2λ−1)cos⁡λ=−aycos⁡λ. \frac{a_y (\sin^2\lambda - 1)}{\cos\lambda} = -a_y \cos\lambda. cosλay(sin2λ−1)=−aycosλ.

因此，第三项简化为 −aycos⁡λ−azsin⁡λ-a_y \cos\lambda - a_z \sin\lambda−aycosλ−azsinλ。代入 SSS 得到

S=rtθesin⁡λcot⁡β+rtcos⁡λsin⁡θe−aycos⁡λ−azsin⁡λ. S = r_t \theta_e \sin\lambda \cot\beta + r_t \cos\lambda \sin\theta_e - a_y \cos\lambda - a_z \sin\lambda. S=rtθesinλcotβ+rtcosλsinθe−aycosλ−azsinλ.

现在，将 SSS 按 sin⁡λ\sin\lambdasinλ 和 cos⁡λ\cos\lambdacosλ 合并同类项：

S=sin⁡λ(rtθecot⁡β−az)+cos⁡λ(rtsin⁡θe−ay). S = \sin\lambda \left( r_t \theta_e \cot\beta - a_z \right) + \cos\lambda \left( r_t \sin\theta_e - a_y \right). S=sinλ(rtθecotβ−az)+cosλ(rtsinθe−ay).

由此可见，SSS 是 sin⁡λ\sin\lambdasinλ 和 cos⁡λ\cos\lambdacosλ 的线性组合。于是，平方根内的表达式变为

(c1)2+(a1sin⁡λ+b1cos⁡λ)2, (c_1)^2 + \bigl( a_1 \sin\lambda + b_1 \cos\lambda \bigr)^2, (c1)2+(a1sinλ+b1cosλ)2,

其中

a1=rtθecot⁡β−az,b1=rtsin⁡θe−ay,c1=rtcos⁡θe−ax. a_1 = r_t \theta_e \cot\beta - a_z, \quad b_1 = r_t \sin\theta_e - a_y, \quad c_1 = r_t \cos\theta_e - a_x. a1=rtθecotβ−az,b1=rtsinθe−ay,c1=rtcosθe−ax.

最终，原表达式可简洁地写为

(a1sin⁡λ+b1cos⁡λ)2+c12. \sqrt{ (a_1 \sin\lambda + b_1 \cos\lambda)^2 + c_1^2 }. (a1sinλ+b1cosλ)2+c12 .

这种化简不仅使表达式更加紧凑，还突出了变量 λ\lambdaλ 的作用方式：它仅通过线性组合 a1sin⁡λ+b1cos⁡λa_1 \sin\lambda + b_1 \cos\lambdaa1sinλ+b1cosλ 影响整体值，而 c1c_1c1 作为常数偏移。这种形式在后续的优化中可能有用，例如求极值或积分。此外，若从几何角度理解，该表达式可以解释为三维空间中某点到某直线的距离，其中 λ\lambdaλ 是旋转参数。无论如何，化简后的形式为理论分析和实际计算都带来了便利。