文章目录
本文由Jzwalliser原创，发布在CSDN平台上，遵循CC 4.0 BY-SA协议。
因此，若需转载/引用本文，请注明作者并附原文链接，且禁止删除/修改本段文字。
违者必究，谢谢配合。
前言
笔者高中牲，之前学习三角函数有关知识时，总容易忘这忘那，所以特意整理了一下，方便复习，这里也分享给大家。
诱导公式
"奇变偶不变，符号看象限"
| 公式一 | 公式二 | 公式三 |
|---|---|---|
| sin ( α + 2 k π ) = sin α \sin(\alpha+2k\pi)=\sin \alpha sin(α+2kπ)=sinα ( k ∈ Z ) (k\in\mathbb Z) (k∈Z) | sin ( − α ) = − sin α \sin(-\alpha)=-\sin \alpha sin(−α)=−sinα | sin ( π − α ) = sin α \sin (\pi-\alpha)=\sin \alpha sin(π−α)=sinα |
| cos ( α + 2 k π ) = cos α \cos(\alpha+2k\pi)=\cos \alpha cos(α+2kπ)=cosα ( k ∈ Z ) (k\in\mathbb Z) (k∈Z) | cos ( − α ) = cos α \cos(-\alpha)=\cos \alpha cos(−α)=cosα | cos ( π − α ) = − cos α \cos (\pi-\alpha)=-\cos \alpha cos(π−α)=−cosα |
| tan ( α + 2 k π ) = tan α \tan(\alpha+2k\pi)=\tan \alpha tan(α+2kπ)=tanα ( k ∈ Z ) (k\in\mathbb Z) (k∈Z) | tan ( − α ) = − tan α \tan (-\alpha)=-\tan \alpha tan(−α)=−tanα | tan ( π − α ) = − tan α \tan (\pi-\alpha)=-\tan \alpha tan(π−α)=−tanα |
| 公式四 | 公式五 | 公式六 |
|---|---|---|
| sin ( π + α ) = − sin α \sin (\pi+\alpha)=-\sin \alpha sin(π+α)=−sinα | sin ( π 2 − α ) = cos α \sin (\dfrac{\pi}{2}-\alpha)=\cos \alpha sin(2π−α)=cosα | sin ( π 2 + α ) = cos α \sin (\dfrac{\pi}{2}+\alpha)=\cos \alpha sin(2π+α)=cosα |
| cos ( π + α ) = − cos α \cos (\pi+\alpha)=-\cos \alpha cos(π+α)=−cosα | cos ( π 2 − α ) = sin α \cos (\dfrac{\pi}{2}-\alpha)=\sin \alpha cos(2π−α)=sinα | cos ( π 2 + α ) = − sin α \cos (\dfrac{\pi}{2}+\alpha)=-\sin \alpha cos(2π+α)=−sinα |
| tan ( π + α ) = tan α \tan (\pi+\alpha)=\tan \alpha tan(π+α)=tanα | tan ( π 2 − α ) = 1 tan α \tan (\dfrac{\pi}{2}-\alpha)=\dfrac{1}{\tan \alpha} tan(2π−α)=tanα1 | tan ( π 2 + α ) = − 1 tan α \tan (\dfrac{\pi}{2}+\alpha)=-\dfrac{1}{\tan \alpha} tan(2π+α)=−tanα1 |
基本公式
同角三角函数关系
sin 2 α + cos 2 α = 1 \sin^2\alpha+\cos^2\alpha=1 sin2α+cos2α=1
sin α cos α = tan α \dfrac{\sin\alpha}{\cos\alpha}=\tan\alpha cosαsinα=tanα
如图所示，取一单位圆 x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1，在单位圆上任取一点 P ( x , y ) P(x,y) P(x,y)
根据正、余弦和正切函数在单位圆内的定义，可得 sin α = y r = y \sin\alpha=\dfrac{y}{r}=y sinα=ry=y， cos α = x r = x \cos\alpha=\dfrac{x}{r}=x cosα=rx=x， tan α = y x \tan\alpha=\dfrac{y}{x} tanα=xy
∴ sin 2 α + cos 2 α = y 2 + x 2 = 1 ， sin α cos α = y x = tan α \therefore \sin^2\alpha+\cos^2\alpha=y^2+x^2=1，\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{y}{x}=\tan\alpha ∴sin2α+cos2α=y2+x2=1，cosαsinα=xy=tanα
和差公式
S ( α ± β ) : sin ( α ± β ) = sin α cos β ± cos α sin β S_{(\alpha\pm\beta)}:\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta S(α±β):sin(α±β)=sinαcosβ±cosαsinβ
C ( α ± β ) : cos ( α ± β ) = cos α cos β ∓ sin α sin β C_{(\alpha\pm\beta)}:\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta C(α±β):cos(α±β)=cosαcosβ∓sinαsinβ
T ( α ± β ) : tan ( α ± β ) = tan α ± tan β 1 ∓ tan α tan β T_{(\alpha\pm\beta)}:\tan(\alpha\pm\beta)=\dfrac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta} T(α±β):tan(α±β)=1∓tanαtanβtanα±tanβ
如图所示，取一单位圆 x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1，在单位圆上取两点 A A A、 B B B，记 ∠ A O x = α \angle AOx=\alpha ∠AOx=α， ∠ B O x = β \angle BOx=\beta ∠BOx=β
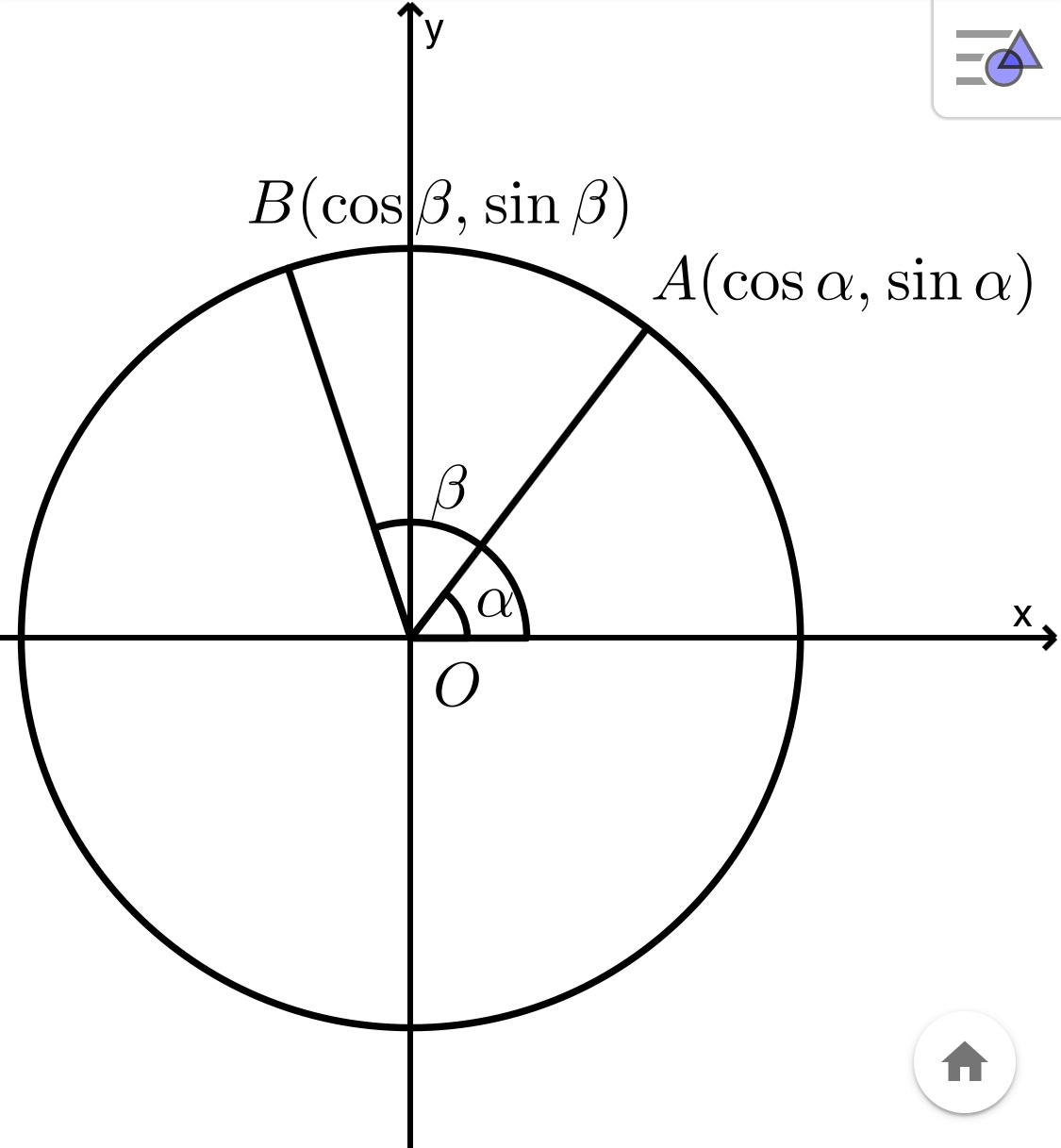（图似乎画的有点问题， α \alpha α、 β \beta β其实应该调换一下位置的，我有时间再改吧）
根据圆的参数方程，可设 A ( cos α , sin α ) A(\cos \alpha,\sin \alpha) A(cosα,sinα)， B ( cos β , sin β ) B(\cos \beta,\sin \beta) B(cosβ,sinβ)
∴ O A → = ( cos α , sin α ) \therefore \overrightarrow{OA}=(\cos \alpha,\sin \alpha) ∴OA =(cosα,sinα)， O B → = ( cos β , sin β ) \overrightarrow{OB}=(\cos \beta,\sin \beta) OB =(cosβ,sinβ)
∵ \because ∵单位圆的半径 r = 1 r=1 r=1
∴ ∣ O A → ∣ = 1 \therefore |\overrightarrow{OA}|=1 ∴∣OA ∣=1， ∣ O B → ∣ = 1 |\overrightarrow{OB}|=1 ∣OB ∣=1
∴ O A → ⋅ O B → = ∣ O A → ∣ ∣ O B → ∣ cos ( α − β ) = 1 × 1 × cos ( α − β ) \therefore \overrightarrow{OA}\cdot\overrightarrow{OB}=|\overrightarrow{OA}||\overrightarrow{OB}|\cos(\alpha-\beta)=1\times1\times\cos(\alpha-\beta) ∴OA ⋅OB =∣OA ∣∣OB ∣cos(α−β)=1×1×cos(α−β)
O A → ⋅ O B → = cos α cos β + sin α sin β \overrightarrow{OA}\cdot\overrightarrow{OB}=\cos\alpha\cos\beta+\sin\alpha\sin\beta OA ⋅OB =cosαcosβ+sinαsinβ
∴ cos ( α − β ) = cos α cos β + sin α sin β \therefore \cos(\alpha-\beta)=\cos \alpha\cos \beta+\sin \alpha\sin \beta ∴cos(α−β)=cosαcosβ+sinαsinβ
用 − β -\beta −β代替掉原来 β \beta β的位置，可得 cos ( α + β ) = cos α cos ( − β ) + sin α sin ( − β ) = cos α cos β − sin α sin β \cos(\alpha+\beta)=\cos \alpha\cos (-\beta)+\sin\alpha\sin (-\beta)=\cos \alpha\cos \beta-\sin \alpha\sin\beta cos(α+β)=cosαcos(−β)+sinαsin(−β)=cosαcosβ−sinαsinβ
用 π 2 − α \dfrac{\pi}{2}-\alpha 2π−α代替掉 cos ( α − β ) = cos α cos β + sin α sin β \cos(\alpha-\beta)=\cos \alpha\cos \beta+\sin \alpha\sin \beta cos(α−β)=cosαcosβ+sinαsinβ中 α \alpha α的位置，可得 cos [ ( π 2 − α ) − β ] = cos ( π 2 − α ) cos β + sin ( π 2 − α ) sin β \cos[(\dfrac{\pi}{2}-\alpha)-\beta]=\cos (\dfrac{\pi}{2}-\alpha)\cos \beta+\sin (\dfrac{\pi}{2}-\alpha)\sin \beta cos[(2π−α)−β]=cos(2π−α)cosβ+sin(2π−α)sinβ
对等式两侧使用诱导公式，可得
sin ( α + β ) = sin α cos β + cos α sin β \sin (\alpha+\beta)=\sin \alpha\cos \beta+\cos \alpha\sin \beta sin(α+β)=sinαcosβ+cosαsinβ
用 − β -\beta −β代替掉原来 β \beta β的位置，可得 sin ( α + β ) = sin α cos ( − β ) + cos α sin ( − β ) = cos α cos β + sin α − β ) \sin(\alpha+\beta)=\sin \alpha\cos (-\beta)+\cos\alpha\sin (-\beta)=\cos \alpha\cos \beta+\sin \alpha-\beta) sin(α+β)=sinαcos(−β)+cosαsin(−β)=cosαcosβ+sinα−β)
由此得到 sin ( α ± β ) = sin α cos β ± cos α sin β \sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta sin(α±β)=sinαcosβ±cosαsinβ、 cos ( α ± β ) = cos α cos β ∓ sin α sin β \cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta cos(α±β)=cosαcosβ∓sinαsinβ
∴ tan ( α ± β ) = sin ( α ± β ) cos ( α ± β ) = sin α cos β ± cos α sin β cos α cos β ∓ sin α sin β = tan α ± tan β 1 ∓ tan α tan β \therefore\tan(\alpha\pm\beta)=\dfrac{\sin(\alpha\pm\beta)}{\cos(\alpha\pm\beta)}=\dfrac{\sin\alpha\cos\beta\pm\cos\alpha\sin\beta}{\cos\alpha\cos\beta\mp\sin\alpha\sin\beta}=\dfrac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta} ∴tan(α±β)=cos(α±β)sin(α±β)=cosαcosβ∓sinαsinβsinαcosβ±cosαsinβ=1∓tanαtanβtanα±tanβ（上下同时除以 cos α cos β \cos\alpha\cos\beta cosαcosβ）
二倍角公式
S 2 α : sin 2 α = 2 sin α cos α S_{2\alpha}:\sin2\alpha=2\sin\alpha\cos\alpha S2α:sin2α=2sinαcosα
C 2 α : cos 2 α = cos 2 α − sin 2 α C_{2\alpha}:\cos2\alpha=\cos^2\alpha-\sin^2\alpha C2α:cos2α=cos2α−sin2α
T 2 α : tan 2 α = 2 tan α 1 − tan 2 α T_{2\alpha}:\tan2\alpha=\dfrac{2\tan\alpha}{1-\tan^{2}\alpha} T2α:tan2α=1−tan2α2tanα
sin 2 α = sin ( α + α ) = sin α cos α + cos α sin α = 2 sin α cos α \sin2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\cos\alpha\sin\alpha=2\sin\alpha\cos\alpha sin2α=sin(α+α)=sinαcosα+cosαsinα=2sinαcosα
cos 2 α = cos ( α + α ) = cos α cos α − sin α sin α = cos 2 α − sin 2 α \cos2\alpha=\cos(\alpha+\alpha)=\cos\alpha\cos\alpha-\sin\alpha\sin\alpha=\cos^2\alpha-\sin^2\alpha cos2α=cos(α+α)=cosαcosα−sinαsinα=cos2α−sin2α
tan 2 α = tan ( α + α ) = tan α + tan α 1 − tan α tan α 2 tan α 1 − tan 2 α \tan2\alpha=\tan(\alpha+\alpha)=\dfrac{\tan\alpha+\tan\alpha}{1-\tan\alpha\tan\alpha}\dfrac{2\tan\alpha}{1-\tan^2\alpha} tan2α=tan(α+α)=1−tanαtanαtanα+tanα1−tan2α2tanα
辅助角公式
a sin α + b cos α = a 2 + b 2 sin ( α + φ ) = a 2 + b 2 cos ( α − θ ) a \sin \alpha+ b \cos \alpha= \sqrt{a^2 + b^2} \sin(\alpha+ \varphi) = \sqrt{a^2 + b^2} \cos(\alpha - \theta) asinα+bcosα=a2+b2 sin(α+φ)=a2+b2 cos(α−θ)
其中 tan φ = b a \tan \varphi= \dfrac{b}{a} tanφ=ab， tan θ = a b \tan \theta = \dfrac{a}{b} tanθ=ba
重要公式
升幂公式
1 + cos 2 α = 2 cos 2 α 1 + \cos 2\alpha= 2 \cos^2 \alpha 1+cos2α=2cos2α
1 − cos 2 α = 2 sin 2 α 1 - \cos 2\alpha= 2 \sin^2 \alpha 1−cos2α=2sin2α
1 + sin 2 α = ( sin α + cos α ) 2 1 + \sin 2\alpha= (\sin \alpha + \cos \alpha)^2 1+sin2α=(sinα+cosα)2
1 − sin 2 α = ( sin α − cos α ) 2 1 - \sin 2\alpha= (\sin \alpha - \cos \alpha)^2 1−sin2α=(sinα−cosα)2
∵ cos 2 α = cos 2 α − sin 2 α \because \cos2\alpha=\cos^2\alpha-\sin^2\alpha ∵cos2α=cos2α−sin2α
∴ cos 2 α = sin 2 α + cos 2 α \therefore \cos^2\alpha=\sin^2\alpha+\cos2\alpha ∴cos2α=sin2α+cos2α
cos 2 α + cos 2 α = sin 2 α + cos 2 α + cos 2 α \cos^2\alpha+\cos^2\alpha=\sin^2\alpha+\cos^2\alpha+\cos 2\alpha cos2α+cos2α=sin2α+cos2α+cos2α
2 cos 2 α = sin 2 α + cos 2 α + cos 2 α 2\cos^2\alpha=\sin^2\alpha+\cos^2\alpha+\cos2\alpha 2cos2α=sin2α+cos2α+cos2α
2 cos 2 α = 1 + cos 2 α 2\cos^2\alpha=1+\cos2\alpha 2cos2α=1+cos2α
∵ cos 2 α = cos 2 α − sin 2 α \because \cos2\alpha=\cos^2\alpha-\sin^2\alpha ∵cos2α=cos2α−sin2α
∴ sin 2 α = cos 2 α − cos 2 α \therefore \sin^2\alpha=\cos^2\alpha-\cos2\alpha ∴sin2α=cos2α−cos2α
sin 2 α + sin 2 α = cos 2 α + sin 2 α − cos 2 α \sin^2\alpha+\sin^2\alpha=\cos^2\alpha+\sin^2\alpha-\cos 2\alpha sin2α+sin2α=cos2α+sin2α−cos2α
2 sin 2 α = cos 2 α + sin 2 α − cos 2 α 2\sin^2\alpha=\cos^2\alpha+\sin^2\alpha-\cos2\alpha 2sin2α=cos2α+sin2α−cos2α
2 sin 2 α = 1 − cos 2 α 2\sin^2\alpha=1-\cos2\alpha 2sin2α=1−cos2α
1 + sin 2 α = sin 2 α + cos 2 α + 2 sin α cos α = ( sin α + cos α ) 2 1+\sin 2\alpha=\sin^2\alpha+\cos^2\alpha+2\sin \alpha\cos \alpha=(\sin \alpha+\cos \alpha)^2 1+sin2α=sin2α+cos2α+2sinαcosα=(sinα+cosα)2
1 − sin 2 α = sin 2 α + cos 2 α − 2 sin α cos α = ( sin α − cos α ) 2 1-\sin 2\alpha=\sin^2\alpha+\cos^2\alpha-2\sin \alpha\cos \alpha=(\sin \alpha-\cos \alpha)^2 1−sin2α=sin2α+cos2α−2sinαcosα=(sinα−cosα)2
降幂公式
sin 2 α = 1 2 ( 1 − cos 2 α ) \sin^2 \alpha = \dfrac{1}{2}(1 - \cos 2\alpha) sin2α=21(1−cos2α)
cos 2 α = 1 2 ( 1 + cos 2 α ) \cos^2 \alpha= \dfrac{1}{2}(1 + \cos 2\alpha) cos2α=21(1+cos2α)
∵ 2 sin 2 α = 1 − cos 2 α \because 2\sin^2\alpha=1-\cos2\alpha ∵2sin2α=1−cos2α
∴ sin 2 α = 1 2 ( 1 − cos 2 α ) \therefore \sin^2\alpha=\dfrac12(1-\cos2\alpha) ∴sin2α=21(1−cos2α)
∵ 2 cos 2 α = 1 + cos 2 α \because 2\cos^2\alpha=1+\cos2\alpha ∵2cos2α=1+cos2α
∴ cos 2 α = 1 2 ( 1 + cos 2 α ) \therefore \cos^2\alpha=\dfrac12(1+\cos2\alpha) ∴cos2α=21(1+cos2α)
逆用倍角公式
sin α = sin 2 α 2 cos α \sin \alpha = \dfrac{\sin 2\alpha}{2 \cos \alpha} sinα=2cosαsin2α
cos α = sin 2 α 2 sin α \cos \alpha = \dfrac{\sin 2\alpha}{2 \sin \alpha} cosα=2sinαsin2α
tan α = tan 2 α ( 1 − tan 2 α ) 2 \tan \alpha = \dfrac{\tan 2\alpha(1 - \tan^2 \alpha)}{2} tanα=2tan2α(1−tan2α)
( cos α + sin α ) ( cos α − sin α ) = cos 2 α − sin 2 α = cos 2 α (\cos \alpha + \sin \alpha)(\cos \alpha - \sin \alpha)=\cos^2 \alpha - \sin^2 \alpha = \cos2\alpha (cosα+sinα)(cosα−sinα)=cos2α−sin2α=cos2α
2 cos 2 α − 1 = 1 − 2 sin 2 α = cos 2 α 2 \cos^2 \alpha - 1 = 1 - 2 \sin^2 \alpha = \cos 2\alpha 2cos2α−1=1−2sin2α=cos2α
∵ sin 2 α = 2 sin α cos α \because\sin 2\alpha=2\sin \alpha\cos \alpha ∵sin2α=2sinαcosα
∴ sin α = sin 2 α 2 cos α \therefore\sin \alpha = \dfrac{\sin 2\alpha}{2 \cos \alpha} ∴sinα=2cosαsin2α， cos α = sin 2 α 2 sin α \cos \alpha = \dfrac{\sin 2\alpha}{2 \sin \alpha} cosα=2sinαsin2α
∵ tan 2 α = 2 tan α 1 − tan 2 α \because \tan2\alpha=\dfrac{2\tan\alpha}{1-\tan^{2}\alpha} ∵tan2α=1−tan2α2tanα
∴ tan α = tan 2 α ( 1 − tan 2 α ) 2 \therefore \tan \alpha = \dfrac{\tan 2\alpha(1 - \tan^2 \alpha)}{2} ∴tanα=2tan2α(1−tan2α)
∵ cos 2 α = cos 2 α − sin 2 α \because\cos2\alpha=\cos^2\alpha-\sin^2\alpha ∵cos2α=cos2α−sin2α
∴ ( cos α + sin α ) ( cos α − sin α ) = cos 2 α − sin 2 α = cos 2 α \therefore(\cos \alpha + \sin \alpha)(\cos \alpha - \sin \alpha)=\cos^2 \alpha - \sin^2 \alpha = \cos2\alpha ∴(cosα+sinα)(cosα−sinα)=cos2α−sin2α=cos2α
∵ sin 2 α = 1 2 ( 1 − cos 2 α ) \because\sin^2 \alpha = \dfrac{1}{2}(1 - \cos 2\alpha) ∵sin2α=21(1−cos2α)， cos 2 α = 1 2 ( 1 + cos 2 α ) \cos^2 \alpha= \dfrac{1}{2}(1 + \cos 2\alpha) cos2α=21(1+cos2α)
∴ 2 cos 2 α − 1 = 1 − 2 sin 2 α = cos 2 α \therefore 2 \cos^2 \alpha - 1 = 1 - 2 \sin^2 \alpha = \cos 2\alpha ∴2cos2α−1=1−2sin2α=cos2α
积化和差
cos α cos β = 1 2 [ cos ( α + β ) + cos ( α − β ) ] \cos\alpha\cos\beta=\dfrac{1}{2}[\cos(\alpha+\beta)+\cos(\alpha-\beta)] cosαcosβ=21[cos(α+β)+cos(α−β)]
sin α sin β = − 1 2 [ cos ( α + β ) − cos ( α − β ) ] \sin\alpha\sin\beta=-\dfrac{1}{2}[\cos(\alpha+\beta)-\cos(\alpha-\beta)] sinαsinβ=−21[cos(α+β)−cos(α−β)]
sin α cos β = 1 2 [ sin ( α + β ) + sin ( α − β ) ] \sin\alpha\cos\beta=\dfrac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha-\beta)] sinαcosβ=21[sin(α+β)+sin(α−β)]
cos α sin β = 1 2 [ sin ( α + β ) − sin ( α − β ) ] \cos\alpha\sin\beta=\dfrac{1}{2}[\sin(\alpha+\beta)-\sin(\alpha-\beta)] cosαsinβ=21[sin(α+β)−sin(α−β)]
1 2 [ cos ( α + β ) + cos ( α − β ) ] = 1 2 ( cos α cos β − sin α sin β + cos α cos β + sin α sin β ) = 1 2 ⋅ 2 cos α cos β = cos α cos β \dfrac{1}{2}[\cos(\alpha+\beta)+\cos(\alpha-\beta)]=\dfrac12(\cos\alpha\cos \beta-\sin \alpha\sin \beta+\cos \alpha\cos \beta+\sin \alpha\sin \beta)=\dfrac12\cdot2\cos \alpha\cos \beta=\cos \alpha\cos \beta 21[cos(α+β)+cos(α−β)]=21(cosαcosβ−sinαsinβ+cosαcosβ+sinαsinβ)=21⋅2cosαcosβ=cosαcosβ
− 1 2 [ cos ( α + β ) − cos ( α − β ) ] = − 1 2 ( cos α cos β − sin α sin β − cos α cos β − sin α sin β ) = − 1 2 ⋅ ( − 2 sin α sin β ) = sin α sin β -\dfrac{1}{2}[\cos(\alpha+\beta)-\cos(\alpha-\beta)]=-\dfrac12(\cos \alpha\cos \beta-\sin \alpha\sin \beta-\cos \alpha\cos \beta-\sin \alpha\sin \beta)=-\dfrac12\cdot(-2\sin \alpha\sin \beta)=\sin \alpha\sin \beta −21[cos(α+β)−cos(α−β)]=−21(cosαcosβ−sinαsinβ−cosαcosβ−sinαsinβ)=−21⋅(−2sinαsinβ)=sinαsinβ
1 2 [ sin ( α + β ) + sin ( α − β ) ] = 1 2 ( sin α cos β + sin β cos α + sin α cos β − sin β cos α ) = 1 2 ⋅ 2 sin α cos β = sin α cos β \dfrac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha-\beta)]=\dfrac12(\sin \alpha\cos \beta+\sin \beta\cos \alpha+\sin \alpha\cos \beta-\sin \beta\cos \alpha)=\dfrac12\cdot2\sin \alpha\cos \beta=\sin \alpha\cos \beta 21[sin(α+β)+sin(α−β)]=21(sinαcosβ+sinβcosα+sinαcosβ−sinβcosα)=21⋅2sinαcosβ=sinαcosβ
1 2 [ sin ( α + β ) − sin ( α − β ) ] = 1 2 ( sin α cos β + sin β cos α − sin α cos β + sin β cos α ) = 1 2 ⋅ 2 sin β cos α = cos α sin β \dfrac{1}{2}[\sin(\alpha+\beta)-\sin(\alpha-\beta)]=\dfrac12(\sin \alpha\cos \beta+\sin \beta\cos \alpha-\sin \alpha\cos \beta+\sin \beta\cos \alpha)=\dfrac12\cdot2\sin \beta\cos \alpha=\cos \alpha\sin \beta 21[sin(α+β)−sin(α−β)]=21(sinαcosβ+sinβcosα−sinαcosβ+sinβcosα)=21⋅2sinβcosα=cosαsinβ
和差化积
cos α + cos β = 2 cos α + β 2 cos α − β 2 \cos\alpha+\cos\beta=2\cos\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2} cosα+cosβ=2cos2α+βcos2α−β
cos α − cos β = − 2 sin α + β 2 sin α − β 2 \cos\alpha-\cos\beta=-2\sin\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2} cosα−cosβ=−2sin2α+βsin2α−β
sin α + sin β = 2 sin α + β 2 cos α − β 2 \sin\alpha+\sin\beta=2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2} sinα+sinβ=2sin2α+βcos2α−β
sin α − sin β = 2 cos α + β 2 sin α − β 2 \sin\alpha-\sin\beta=2\cos\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2} sinα−sinβ=2cos2α+βsin2α−β
令 A + B = α A+B=\alpha A+B=α， A − B = β A-B=\beta A−B=β
∴ { A + B = α A − B = β \therefore\left\{ \begin{aligned}&A+B=\alpha\\&A-B=\beta\end{aligned}\right. ∴{A+B=αA−B=β
解得 { A = α + β 2 B = α − β 2 \left\{ \begin{aligned}&A=\dfrac{\alpha+\beta}{2}\\&B=\dfrac{\alpha-\beta}{2}\end{aligned}\right. ⎩ ⎨ ⎧A=2α+βB=2α−β
cos α + cos β = cos ( A + B ) + cos ( A − B ) = cos A cos B − sin A sin B + cos A cos B + sin A sin B = 2 cos A cos B = 2 cos α + β 2 cos α − β 2 \cos\alpha+\cos\beta=\cos (A+B)+\cos (A-B)=\cos A\cos B-\sin A\sin B+\cos A\cos B+\sin A\sin B=2\cos A\cos B=2\cos\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2} cosα+cosβ=cos(A+B)+cos(A−B)=cosAcosB−sinAsinB+cosAcosB+sinAsinB=2cosAcosB=2cos2α+βcos2α−β
cos α − cos β = cos ( A + B ) − cos ( A − B ) = cos A cos B − sin A sin B − cos A cos B − sin A sin B = − 2 sin A sin B = − 2 sin α + β 2 sin α − β 2 \cos\alpha-\cos\beta=\cos (A+B)-\cos (A-B)=\cos A\cos B-\sin A\sin B-\cos A\cos B-\sin A\sin B=-2\sin A\sin B=-2\sin\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2} cosα−cosβ=cos(A+B)−cos(A−B)=cosAcosB−sinAsinB−cosAcosB−sinAsinB=−2sinAsinB=−2sin2α+βsin2α−β
sin α + sin β = sin ( A + B ) + sin ( A − B ) = sin A cos B + sin B cos A + sin A cos B − sin B cos A = 2 sin A cos B = 2 sin α + β 2 cos α − β 2 \sin\alpha+\sin\beta=\sin (A+B)+\sin (A-B)=\sin A\cos B+\sin B\cos A+\sin A\cos B-\sin B\cos A=2\sin A\cos B=2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2} sinα+sinβ=sin(A+B)+sin(A−B)=sinAcosB+sinBcosA+sinAcosB−sinBcosA=2sinAcosB=2sin2α+βcos2α−β
sin α − sin β = sin ( A + B ) − sin ( A − B ) = sin A cos B + sin B cos A − sin A cos B + sin B cos A = 2 sin B cos A = 2 cos α + β 2 sin α − β 2 \sin\alpha-\sin\beta=\sin (A+B)-\sin (A-B)=\sin A\cos B+\sin B\cos A-\sin A\cos B+\sin B\cos A=2\sin B\cos A=2\cos\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2} sinα−sinβ=sin(A+B)−sin(A−B)=sinAcosB+sinBcosA−sinAcosB+sinBcosA=2sinBcosA=2cos2α+βsin2α−β
半角公式
sin α 2 = ± 1 − cos α 2 \sin\dfrac{\alpha}{2}=\pm\sqrt{\dfrac{1-\cos\alpha}{2}} sin2α=±21−cosα
cos α 2 = ± 1 + cos α 2 \cos\dfrac{\alpha}{2}=\pm\sqrt{\dfrac{1+\cos\alpha}{2}} cos2α=±21+cosα
tan α 2 = ± 1 − cos α 1 + cos α \tan\dfrac{\alpha}{2}=\pm\sqrt{\dfrac{1-\cos\alpha}{1+\cos\alpha}} tan2α=±1+cosα1−cosα
tan α 2 = 1 − cos α sin α = sin α 1 + cos α \tan\dfrac{\alpha}{2}=\dfrac{1-\cos\alpha}{\sin\alpha}=\dfrac{\sin\alpha}{1+\cos\alpha} tan2α=sinα1−cosα=1+cosαsinα
∵ 1 + cos 2 α = 2 cos 2 α \because1+\cos 2\alpha=2\cos^2\alpha ∵1+cos2α=2cos2α
∴ 1 + cos α = 2 cos 2 α 2 \therefore1+\cos \alpha=2\cos^2\dfrac{\alpha}{2} ∴1+cosα=2cos22α
∴ cos α 2 = ± 1 + cos α 2 \therefore\cos\dfrac{\alpha}{2}=\pm\sqrt{\dfrac{1+\cos\alpha}{2}} ∴cos2α=±21+cosα
∵ 1 − cos 2 α = 2 sin 2 α \because1-\cos 2\alpha=2\sin^2\alpha ∵1−cos2α=2sin2α
∴ 1 − cos α = 2 sin 2 α 2 \therefore1-\cos \alpha=2\sin^2\dfrac{\alpha}{2} ∴1−cosα=2sin22α
∴ sin α 2 = ± 1 − cos α 2 \therefore\sin\dfrac{\alpha}{2}=\pm\sqrt{\dfrac{1-\cos\alpha}{2}} ∴sin2α=±21−cosα
∴ tan α 2 = sin α 2 cos α 2 = ± 1 − cos α 1 + cos α \therefore\tan\dfrac{\alpha}{2}=\dfrac{\sin\dfrac{\alpha}{2}}{\cos \dfrac{\alpha}{2}}=\pm\sqrt{\dfrac{1-\cos\alpha}{1+\cos\alpha}} ∴tan2α=cos2αsin2α=±1+cosα1−cosα
tan α 2 = sin α 2 cos α 2 = 2 sin α 2 cos α 2 2 cos 2 α 2 = sin α 1 + cos α \tan \dfrac{\alpha}{2}=\dfrac{\sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}}=\dfrac{2\sin \frac{\alpha}{2}\cos \frac{\alpha}{2}}{2\cos^2\frac{\alpha}{2}}=\dfrac{\sin \alpha}{1+\cos \alpha} tan2α=cos2αsin2α=2cos22α2sin2αcos2α=1+cosαsinα
tan α 2 = sin α 2 cos α 2 = 2 sin 2 α 2 2 sin α 2 cos α 2 = 1 − cos α sin α \tan \dfrac{\alpha}{2}=\dfrac{\sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}}=\dfrac{2\sin^2\frac{\alpha}{2}}{2\sin \frac{\alpha}{2}\cos\frac{\alpha}{2}}=\dfrac{1-\cos \alpha}{\sin \alpha} tan2α=cos2αsin2α=2sin2αcos2α2sin22α=sinα1−cosα
其它公式
三倍角公式
sin 3 α = 3 sin α − 4 sin 3 α \sin 3\alpha = 3 \sin \alpha - 4 \sin^3 \alpha sin3α=3sinα−4sin3α
cos 3 α = 4 cos 3 α − 3 cos α \cos 3\alpha = 4 \cos^3 \alpha - 3 \cos \alpha cos3α=4cos3α−3cosα
tan 3 α = 3 tan α − tan 3 α 1 − 3 tan 2 α \tan 3\alpha = \dfrac{3 \tan \alpha - \tan^3 \alpha}{1 - 3 \tan^2 \alpha} tan3α=1−3tan2α3tanα−tan3α
sin 3 α = sin ( 2 α + α ) = sin 2 α cos α + cos 2 α sin α = 2 sin α ( 1 − sin 2 α ) + ( 1 − 2 sin 2 α ) sin α = 3 sin α − 4 sin 3 α \sin 3\alpha=\sin (2\alpha+\alpha)=\sin 2\alpha\cos \alpha+\cos 2\alpha\sin \alpha=2\sin \alpha(1-\sin^2\alpha)+(1-2\sin^2\alpha)\sin \alpha=3\sin \alpha-4\sin^3\alpha sin3α=sin(2α+α)=sin2αcosα+cos2αsinα=2sinα(1−sin2α)+(1−2sin2α)sinα=3sinα−4sin3α
cos 3 α = cos ( 2 α + α ) = cos 2 α cos α − sin 2 α sin α = ( 2 cos 2 α − 1 ) cos α − 2 ( 1 − cos 2 α ) cos α = 4 cos 3 α − 3 cos α \cos 3\alpha=\cos (2\alpha+\alpha)=\cos 2\alpha\cos \alpha-\sin 2\alpha\sin \alpha=(2\cos^2\alpha-1)\cos \alpha-2(1-\cos^2\alpha)\cos \alpha=4\cos^3\alpha-3\cos \alpha cos3α=cos(2α+α)=cos2αcosα−sin2αsinα=(2cos2α−1)cosα−2(1−cos2α)cosα=4cos3α−3cosα
tan 3 α = sin 3 α cos 3 α = sin ( α + 2 α ) cos ( α + 2 α ) = sin α cos 2 α + cos α sin 2 α cos α cos 2 α − sin α sin 2 α = sin α ( cos 2 α − sin 2 α ) + cos α ⋅ 2 sin α cos α cos α ( cos 2 α − sin 2 α ) − sin α ⋅ 2 sin α cos α = sin α cos 2 α − sin 3 α + 2 sin α cos 2 α cos 3 α − sin 2 α cos α − 2 sin 2 α cos α = 3 sin α cos 2 α − sin 3 α cos 3 α − 3 sin 2 α cos α = 3 tan α − tan 3 α 1 − 3 tan 2 α \tan 3\alpha=\dfrac{\sin 3\alpha}{\cos 3\alpha}=\dfrac{\sin (\alpha+2\alpha)}{\cos (\alpha+2\alpha)}=\dfrac{\sin \alpha\cos 2\alpha+\cos \alpha\sin 2\alpha}{\cos \alpha\cos 2\alpha-\sin \alpha\sin 2\alpha}=\dfrac{\sin \alpha(\cos^2\alpha-\sin ^2\alpha)+\cos \alpha\cdot2\sin \alpha\cos\alpha}{\cos \alpha(\cos ^2\alpha-\sin ^2\alpha)-\sin \alpha\cdot2\sin \alpha\cos \alpha}=\dfrac{\sin \alpha\cos^2\alpha-\sin^3\alpha+2\sin \alpha\cos^2\alpha}{\cos^3\alpha-\sin ^2\alpha\cos \alpha-2\sin^2\alpha\cos \alpha}=\dfrac{3\sin \alpha\cos^2\alpha-\sin^3\alpha}{\cos^3\alpha-3\sin^2\alpha\cos \alpha}=\dfrac{3\tan \alpha-\tan^3\alpha}{1-3\tan^2\alpha} tan3α=cos3αsin3α=cos(α+2α)sin(α+2α)=cosαcos2α−sinαsin2αsinαcos2α+cosαsin2α=cosα(cos2α−sin2α)−sinα⋅2sinαcosαsinα(cos2α−sin2α)+cosα⋅2sinαcosα=cos3α−sin2αcosα−2sin2αcosαsinαcos2α−sin3α+2sinαcos2α=cos3α−3sin2αcosα3sinαcos2α−sin3α=1−3tan2α3tanα−tan3α
万能公式
sin α = 2 tan α 2 tan 2 α 2 + 1 \sin \alpha=\dfrac{2\tan \dfrac{\alpha}{2}}{\tan^2\dfrac{\alpha}{2}+1} sinα=tan22α+12tan2α
cos α = 1 − tan 2 α 2 1 + tan 2 α 2 \cos \alpha=\dfrac{1-\tan^2\dfrac{\alpha}{2}}{1+\tan^2\dfrac{\alpha}{2}} cosα=1+tan22α1−tan22α
tan α = 2 tan α 2 1 − tan 2 α 2 \tan \alpha=\dfrac{2\tan \dfrac{\alpha}{2}}{1-\tan^2\dfrac{\alpha}{2}} tanα=1−tan22α2tan2α
sin α = 2 sin α 2 cos α 2 = 2 sin α 2 cos α 2 2 sin 2 α 2 + cos 2 α 2 = 2 tan α 2 tan 2 α 2 + 1 \sin \alpha=2\sin\dfrac{\alpha}{2}\cos \dfrac{\alpha}{2}=\dfrac{2\sin \dfrac{\alpha}{2}\cos \dfrac{\alpha}{2}}{2\sin^2\dfrac{\alpha}{2}+\cos^2\dfrac{\alpha}{2}}=\dfrac{2\tan \dfrac{\alpha}{2}}{\tan^2\dfrac{\alpha}{2}+1} sinα=2sin2αcos2α=2sin22α+cos22α2sin2αcos2α=tan22α+12tan2α
cos α = cos 2 α 2 − sin 2 α 2 = cos 2 α 2 − sin 2 α 2 sin 2 α 2 + cos 2 α 2 = 1 − tan 2 α 2 1 + tan 2 α 2 \cos \alpha=\cos^2\dfrac{\alpha}{2}-\sin^2\dfrac{\alpha}{2}=\dfrac{\cos^2\dfrac{\alpha}{2}-\sin^2\dfrac{\alpha}{2}}{\sin^2\dfrac{\alpha}{2}+\cos^2\dfrac{\alpha}{2}}=\dfrac{1-\tan^2\dfrac{\alpha}{2}}{1+\tan^2\dfrac{\alpha}{2}} cosα=cos22α−sin22α=sin22α+cos22αcos22α−sin22α=1+tan22α1−tan22α
tan α = 2 tan α 2 1 − tan 2 α 2 \tan \alpha=\dfrac{2\tan \dfrac{\alpha}{2}}{1-\tan^2\dfrac{\alpha}{2}} tanα=1−tan22α2tan2α
类平方差公式
sin 2 α − sin 2 β = sin ( α + β ) sin ( α − β ) \sin^2 \alpha - \sin^2 \beta = \sin(\alpha + \beta) \sin(\alpha - \beta) sin2α−sin2β=sin(α+β)sin(α−β)
cos 2 α − cos 2 β = − sin ( α + β ) sin ( α − β ) \cos^2 \alpha - \cos^2 \beta = -\sin(\alpha + \beta) \sin(\alpha - \beta) cos2α−cos2β=−sin(α+β)sin(α−β)
cos 2 α − sin 2 β = cos ( α + β ) cos ( α − β ) \cos^2 \alpha - \sin^2 \beta = \cos(\alpha + \beta) \cos(\alpha - \beta) cos2α−sin2β=cos(α+β)cos(α−β)
sin ( α + β ) sin ( α − β ) = ( sin α cos β + sin β cos α ) ( sin α cos β − sin β cos α ) = sin 2 α cos 2 β − sin 2 β cos 2 α = sin 2 α ( 1 − sin 2 β ) − sin 2 β ( 1 − sin 2 α ) = sin 2 α − sin 2 α sin 2 β − sin 2 β + sin 2 α sin 2 β = sin 2 α − sin 2 β \sin(\alpha + \beta) \sin(\alpha - \beta)=(\sin \alpha\cos \beta+\sin \beta\cos \alpha)(\sin \alpha\cos \beta-\sin \beta\cos \alpha)=\sin^2\alpha\cos^2\beta-\sin^2\beta\cos^2\alpha=\sin^2\alpha(1-\sin^2\beta)-\sin^2\beta(1-\sin^2\alpha)=\sin^2\alpha-\sin^2\alpha\sin^2\beta-\sin^2\beta+\sin^2\alpha\sin^2\beta=\sin^2 \alpha - \sin^2 \beta sin(α+β)sin(α−β)=(sinαcosβ+sinβcosα)(sinαcosβ−sinβcosα)=sin2αcos2β−sin2βcos2α=sin2α(1−sin2β)−sin2β(1−sin2α)=sin2α−sin2αsin2β−sin2β+sin2αsin2β=sin2α−sin2β
− sin ( α + β ) sin ( α − β ) = − ( sin α cos β + sin β cos α ) ( sin α cos β − sin β cos α ) = − ( sin 2 α cos 2 β − sin 2 β cos 2 α ) = − [ ( 1 − cos 2 α ) cos 2 β − ( 1 − cos 2 β ) cos 2 α ] = − ( cos 2 β − cos 2 α cos 2 β − cos 2 α + cos 2 α cos 2 β ) = − ( cos 2 β − cos 2 α ) = cos 2 α − cos 2 β -\sin(\alpha+\beta)\sin (\alpha-\beta)=-(\sin \alpha\cos \beta+\sin \beta\cos \alpha)(\sin \alpha\cos \beta-\sin \beta\cos \alpha)=-(\sin^2\alpha\cos^2\beta-\sin^2\beta\cos^2\alpha)=-[(1-\cos^2\alpha)\cos^2\beta-(1-\cos^2\beta)\cos^2\alpha]=-(\cos^2\beta-\cos^2\alpha\cos^2\beta-\cos^2\alpha+\cos^2\alpha\cos^2\beta)=-(\cos^2\beta-\cos^2\alpha)=\cos^2 \alpha - \cos^2 \beta −sin(α+β)sin(α−β)=−(sinαcosβ+sinβcosα)(sinαcosβ−sinβcosα)=−(sin2αcos2β−sin2βcos2α)=−[(1−cos2α)cos2β−(1−cos2β)cos2α]=−(cos2β−cos2αcos2β−cos2α+cos2αcos2β)=−(cos2β−cos2α)=cos2α−cos2β
cos ( α + β ) cos ( α − β ) = ( cos α cos β − sin α sin β ) ( cos α cos β + sin α sin β ) = cos 2 α cos 2 β − sin 2 α sin 2 β = cos 2 α ( 1 − sin 2 β ) − ( 1 − cos 2 α ) sin 2 β = cos 2 α − cos 2 α sin 2 β − sin 2 β + sin 2 β cos 2 α = cos 2 α − sin 2 β \cos(\alpha + \beta) \cos(\alpha - \beta)=(\cos \alpha\cos \beta-\sin \alpha\sin \beta)(\cos \alpha\cos \beta+\sin \alpha\sin \beta)=\cos^2\alpha\cos^2\beta-\sin^2\alpha\sin^2\beta=\cos^2\alpha(1-\sin^2\beta)-(1-\cos^2\alpha)\sin^2\beta=\cos^2\alpha-\cos^2\alpha\sin^2\beta-\sin^2\beta+\sin^2\beta\cos^2\alpha=\cos^2 \alpha - \sin^2 \beta cos(α+β)cos(α−β)=(cosαcosβ−sinαsinβ)(cosαcosβ+sinαsinβ)=cos2αcos2β−sin2αsin2β=cos2α(1−sin2β)−(1−cos2α)sin2β=cos2α−cos2αsin2β−sin2β+sin2βcos2α=cos2α−sin2β
重要结论
常见辅助角结论
sin x ± cos x = 2 sin ( x ± π 4 ) \sin x \pm \cos x = \sqrt{2} \sin(x \pm \dfrac{\pi}{4}) sinx±cosx=2 sin(x±4π)
cos x ± sin x = 2 cos ( α ∓ π 4 ) \cos x \pm \sin x = \sqrt{2} \cos(\alpha \mp \dfrac{\pi}{4}) cosx±sinx=2 cos(α∓4π)
sin x ± 3 cos x = 2 sin ( x ± π 3 ) \sin x \pm \sqrt{3} \cos x = 2 \sin(x \pm \dfrac{\pi}{3}) sinx±3 cosx=2sin(x±3π)
cos x ± 3 sin x = 2 cos ( x ∓ π 3 ) \cos x \pm \sqrt{3} \sin x = 2 \cos(x \mp \dfrac{\pi}{3}) cosx±3 sinx=2cos(x∓3π)
特殊三角函数
| 1 5 ∘ 15^\circ 15∘ | 1 8 ∘ 18^\circ 18∘ | 3 6 ∘ 36^\circ 36∘ |
|---|---|---|
| sin 1 5 ∘ = 6 − 2 4 \sin15^{\circ}=\dfrac{\sqrt{6}-\sqrt2}{4} sin15∘=46 −2 | sin 1 8 ∘ = 5 − 1 4 \sin18^{\circ}=\dfrac{\sqrt{5}-1}{4} sin18∘=45 −1 | sin 3 6 ∘ = 10 − 2 5 4 \sin36^{\circ}=\dfrac{\sqrt{10-2\sqrt{5}}}{4} sin36∘=410−25 |
| cos 1 5 ∘ = 6 + 2 4 \cos15^{\circ}=\dfrac{\sqrt{6}+\sqrt{2}}{4} cos15∘=46 +2 | cos 1 8 ∘ = 10 + 2 5 4 \cos18^{\circ}=\dfrac{\sqrt{10+2\sqrt{5}}}{4} cos18∘=410+25 | cos 3 6 ∘ = 5 + 1 4 \cos36^{\circ}=\dfrac{\sqrt5+1}{4} cos36∘=45 +1 |
| tan 1 5 ∘ = 2 − 3 \tan15^{\circ}=2-\sqrt{3} tan15∘=2−3 | tan 1 8 ∘ = 5 − 1 10 + 2 5 \tan18^{\circ}=\dfrac{\sqrt{5}-1}{\sqrt{10+2\sqrt{5}}} tan18∘=10+25 5 −1 | tan 3 6 ∘ = 10 − 2 5 5 + 1 \tan36^{\circ}=\dfrac{\sqrt{10-2\sqrt{5}}}{\sqrt{5}+1} tan36∘=5 +110−25 |
三角形内常见结论
sin A + sin B + sin C = 4 cos A 2 cos B 2 cos C 2 \sin A+\sin B+\sin C=4\cos \dfrac{A}{2}\cos \dfrac{B}{2}\cos \dfrac{C}{2} sinA+sinB+sinC=4cos2Acos2Bcos2C
tan A + tan B + tan C = tan A ⋅ tan B ⋅ tan C \tan A+\tan B+\tan C=\tan A\cdot\tan B\cdot\tan C tanA+tanB+tanC=tanA⋅tanB⋅tanC（斜三角形）