正弦函数与椭圆的关系

在数学领域中，正弦函数与椭圆之间的关系是一个既深刻又迷人的话题。这种联系不仅体现在直观的几何表示上，更深入到数学分析的核心领域。本文将全面探讨正弦函数与椭圆之间的双重关系：浅层的参数方程联系和深层的椭圆函数联系，揭示数学概念之间的内在统一性。

椭圆参数方程：直观的几何联系

圆的参数方程是我们熟悉的数学表达：对于单位圆，其参数方程为 x=cos⁡(t)x = \cos(t)x=cos(t)，y=sin⁡(t)y = \sin(t)y=sin(t)，其中参数 ttt 表示圆上一点与原点连线和x轴正方向的夹角。

椭圆可以视为圆在坐标轴方向上按不同比例拉伸的结果。因此，中心在原点、半长轴为 aaa、半短轴为 bbb 的椭圆参数方程自然可以表示为：

x=a⋅cos⁡(t)x = a \cdot \cos(t)x=a⋅cos(t)
y=b⋅sin⁡(t)y = b \cdot \sin(t)y=b⋅sin(t)

这里的参数 ttt 被称为偏心角，虽然不再具有圆中那样直观的角度意义，但仍然是描述椭圆轨迹的极佳参数。

从参数方程的角度看，正弦和余弦函数是构建椭圆轨迹的基础数学元素，这是两者最直接、最易于理解的关系。

椭圆积分与椭圆函数：数学本质的深度联系

圆弧长问题的启示

要理解正弦函数与椭圆的深层联系，最佳起点是经典的圆弧长问题。对于单位圆 y=1−x2y = \sqrt{1-x^2}y=1−x2 ，从 x=0x=0x=0 到 x=Xx=Xx=X 的弧长公式为：

s=∫0Xdx1−x2s = \int_{0}^{X} \frac{dx}{\sqrt{1-x^2}}s=∫0X1−x2 dx

这个积分的解就是反正弦函数：s=arcsin⁡(X)s = \arcsin(X)s=arcsin(X)

如果将这个过程逆转，即已知弧长 uuu，求对应的 xxx 坐标，我们就得到了正弦函数：X=sin⁡(u)X = \sin(u)X=sin(u)。因此，正弦函数可以被定义为"弧长积分"的逆运算。

椭圆弧长问题的挑战

当我们转向椭圆弧长问题时，情况变得复杂。对于椭圆 x2a2+y2b2=1\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1a2x2+b2y2=1，其弧长积分会呈现更复杂的形式。计算从 x=0x=0x=0 到 x=Xx=Xx=X 的弧长，会得到如下积分：

s=∫0Xdx(1−x2)(1−k2x2)s = \int_{0}^{X} \frac{dx}{\sqrt{(1-x^2)(1-k^2x^2)}}s=∫0X(1−x2)(1−k2x2) dx

其中 kkk 是与椭圆离心率相关的参数（模数）。

数学家们发现，这类积分无法用初等函数（三角函数、指数函数、对数函数等）表示，它们构成了一类全新的函数------椭圆积分。

椭圆函数的诞生

面对这一难题，数学家采取了与定义正弦函数相似的策略：对椭圆积分进行逆运算。

定义第一类不完全椭圆积分：

u=∫0ϕdθ1−k2sin⁡2θu = \int_{0}^{\phi} \frac{d\theta}{\sqrt{1-k^2\sin^2\theta}}u=∫0ϕ1−k2sin2θ dθ

然后将这个关系逆转，定义 ϕ\phiϕ 为 uuu 的函数：

ϕ=am⁡(u,k)（"am"代表振幅）\phi = \operatorname{am}(u, k) \quad \text{（"am"代表振幅）}ϕ=am(u,k)（"am"代表振幅）

接着，仿照从振幅定义正弦和余弦的方法，定义了两个核心的椭圆函数：

sn⁡(u,k)=sin⁡(ϕ)=sin⁡(am⁡(u,k))\operatorname{sn}(u, k) = \sin(\phi) = \sin(\operatorname{am}(u, k))sn(u,k)=sin(ϕ)=sin(am(u,k))
cn⁡(u,k)=cos⁡(ϕ)=cos⁡(am⁡(u,k))\operatorname{cn}(u, k) = \cos(\phi) = \cos(\operatorname{am}(u, k))cn(u,k)=cos(ϕ)=cos(am(u,k))

这里的 sn⁡\operatorname{sn}sn 和 cn⁡\operatorname{cn}cn 就是雅可比椭圆函数。

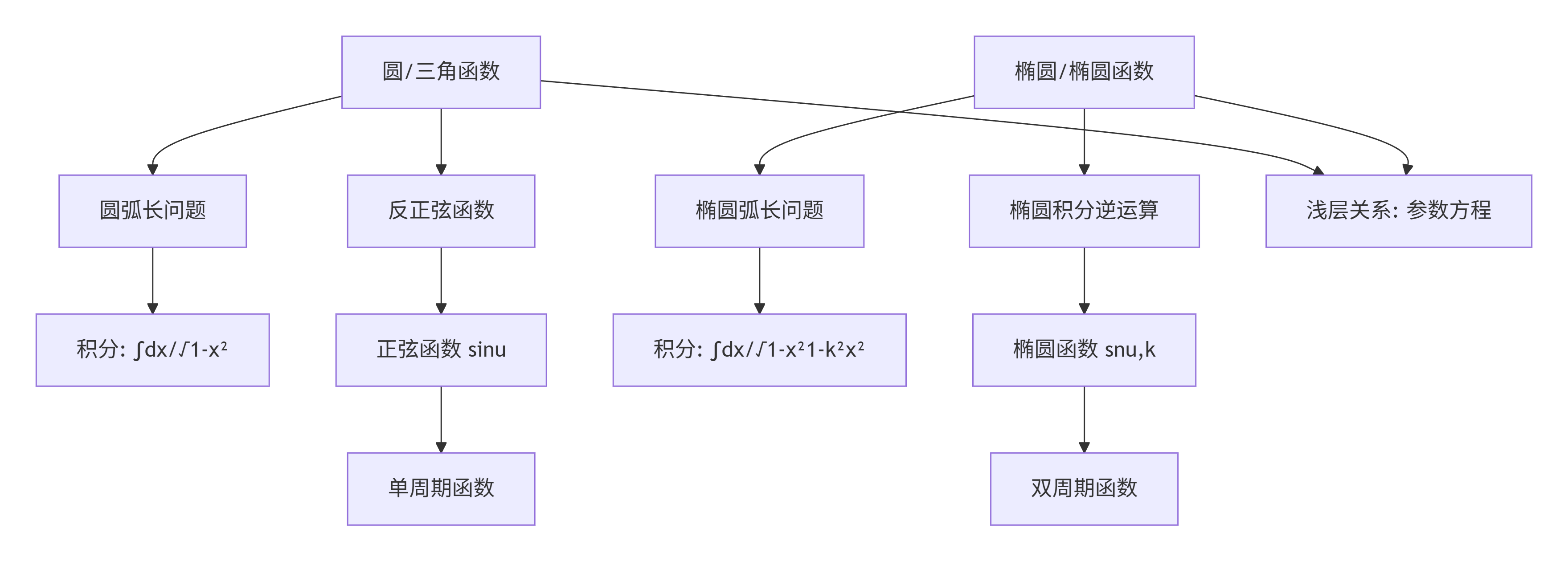
圆与椭圆的数学类比

特征	圆/三角函数	椭圆/椭圆函数
核心问题	圆弧长计算	椭圆弧长计算
产生的积分	∫dx1−x2\int \frac{dx}{\sqrt{1-x^2}}∫1−x2 dx	∫dx(1−x2)(1−k2x2)\int \frac{dx}{\sqrt{(1-x^2)(1-k^2x^2)}}∫(1−x2)(1−k2x2) dx
积分结果	arcsin⁡(x)\arcsin(x)arcsin(x)	椭圆积分
逆运算定义	sin⁡(u)\sin(u)sin(u), cos⁡(u)\cos(u)cos(u)	sn⁡(u,k)\operatorname{sn}(u,k)sn(u,k), cn⁡(u,k)\operatorname{cn}(u,k)cn(u,k)
周期性	单周期函数	双周期函数

这一类比极为深刻：正弦函数是圆弧长积分的逆运算，而椭圆函数是椭圆弧长积分的逆运算。因此，椭圆函数被视为三角函数在椭圆领域的自然推广，共享许多性质（如周期性、代数关系），但更为复杂丰富，特别是具有双周期性这一关键特性。

椭圆周长的计算与正弦函数的核心作用

椭圆周长问题的难点

圆的周长公式 C=2πrC=2\pi rC=2πr 简洁优美，这源于圆的高度对称性。而椭圆（方程 x2a2+y2b2=1\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1a2x2+b2y2=1，其中 aaa 为半长轴，bbb 为半短轴）的对称性较低，导致其周长计算更为复杂。

通过微积分推导椭圆弧长，标准弧长公式为：

s=∫1+(dydx)2dxs = \int \sqrt{1 + \left( \frac{dy}{dx} \right)^2} dxs=∫1+(dxdy)2 dx

对椭圆方程进行隐函数求导和代数变换后，最终得到的椭圆周长公式为：

C=4a∫0π/21−e2sin⁡2θdθC = 4a \int_{0}^{\pi/2} \sqrt{1 - e^2\sin^2\theta} d\thetaC=4a∫0π/21−e2sin2θ dθ

其中：

• aaa 是半长轴
• eee 是椭圆离心率，定义为 e=1−b2a2e = \sqrt{1 - \frac{b^2}{a^2}}e=1−a2b2
• θ\thetaθ 是椭圆参数方程中的参数

第二类完全椭圆积分

积分 ∫0π/21−e2sin⁡2θdθ\int_{0}^{\pi/2} \sqrt{1 - e^2\sin^2\theta} d\theta∫0π/21−e2sin2θ dθ 在数学上称为第二类完全椭圆积分，通常表示为 E(e)E(e)E(e) 或 E(k)E(k)E(k)（其中 k=ek=ek=e 为模数）。

因此，椭圆周长的精确公式可简洁表示为：

C=4a⋅E(e)C = 4a \cdot E(e)C=4a⋅E(e)

这就是正弦函数与椭圆周长最直接的关系：椭圆周长的精确值等于4倍半长轴乘以一个以离心率为模数的第二类完全椭圆积分，而这个积分的被积函数核心就是 1−e2sin⁡2θ\sqrt{1 - e^2\sin^2\theta}1−e2sin2θ 。

近似计算方法

由于精确公式涉及复杂积分，实际应用中常使用近似公式。最著名的是拉马努金近似公式：

C≈π[3(a+b)−(3a+b)(a+3b)]C \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right]C≈π[3(a+b)−(3a+b)(a+3b) ]

此公式精度极高，是对包含正弦函数的积分进行代数近似的结果。

其他常见近似包括基于平均半径的方法：

C≈2πa2+b22或C≈2πa4+b424C \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}} \quad \text{或} \quad C \approx 2\pi \sqrt[4]{\frac{a^4 + b^4}{2}}C≈2π2a2+b2 或C≈2π42a4+b4

椭圆函数的性质与应用

椭圆函数不仅具有理论价值，在物理学和工程学中也有广泛应用：

1. 双周期性：椭圆函数在复平面上有两个周期，这一性质在晶体学中有重要应用。

2. 非线性振动：许多非线性振动系统可以用椭圆函数描述，如大振幅摆的运动。

3. 信号处理：椭圆滤波器在信号处理中提供锐利的截止特性。

4. 密码学：椭圆曲线密码学基于椭圆曲线的数学性质，是现代密码学的重要分支。

结论

正弦函数与椭圆的关系存在两个层面：

1. 浅层关系：正弦和余弦是描述椭圆轨迹的参数方程组成部分，这一关系直观且易于理解。

2. 深层关系：通过椭圆积分的逆运算定义的椭圆函数，是正弦函数概念的直接推广和深化。正如正弦函数解决圆弧长问题，椭圆函数解决椭圆弧长问题。

这种关系体现了数学的统一性与深度，展示了简单概念如何通过推广和发展，形成更为丰富复杂的数学理论。正弦函数与椭圆的联系不仅是数学美的体现，也是数学工具在实际问题中强大应用能力的证明。

附录

数学术语词汇表

单词（短语）	音标	词性	词根/词缀	释义	搭配	例句
elliptic	/ɪˈlɪptɪk/	adj.	ellips(is)+tic	椭圆的	elliptic integral, elliptic function	Elliptic functions have two distinct periods.
eccentricity	/ˌeksenˈtrɪsəti/	n.	ec+centr+icity	离心率	orbital eccentricity	The eccentricity of an ellipse measures its deviation from a circle.
parameterization	/pəˌræmɪtəraɪˈzeɪʃən/	n.	para+meter+ization	参数化	curve parameterization	The parameterization of the ellipse uses trigonometric functions.
periodicity	/ˌpɪəriəˈdɪsəti/	n.	period+icity	周期性	double periodicity	Elliptic functions exhibit double periodicity in the complex plane.
integral	/ˈɪntɪɡrəl/	n.	in+tegral	积分	elliptic integral, definite integral	The arc length of an ellipse leads to an elliptic integral.
amplitude	/ˈæmplɪtjuːd/	n.	ampli+tude	振幅	Jacobian amplitude	The amplitude function is central to defining Jacobian elliptic functions.
modulus	/ˈmɒdjʊləs/	n.	mod(e)+ulus	模数	elliptic modulus	The modulus k determines the shape of elliptic functions.
approximation	/əˌprɒksɪˈmeɪʃən/	n.	ap+proxim+ation	近似法	Ramanujan's approximation	Ramanujan developed accurate approximations for elliptic integrals.

核心关键词

1. 椭圆积分 (Elliptic Integral)
2. 椭圆函数 (Elliptic Function)
3. 参数方程 (Parametric Equation)
4. 离心率 (Eccentricity)
5. 双周期性 (Double Periodicity)
6. 弧长 (Arc Length)
7. 雅可比椭圆函数 (Jacobi Elliptic Functions)
8. 第二类完全椭圆积分 (Complete Elliptic Integral of the Second Kind)
9. 模数 (Modulus)

Python示例：椭圆周长计算

import numpy as np
from scipy.special import ellipe

def ellipse_perimeter(a, b, method='exact'):
    """
    计算椭圆周长
    
    参数:
    a -- 半长轴
    b -- 半短轴
    method -- 计算方法: 'exact'（精确）或 'ramanujan'（拉马努金近似）
    
    返回:
    椭圆周长值
    """
    if method == 'exact':
        # 精确计算方法：使用第二类完全椭圆积分
        e_sq = 1 - (b**2 / a**2)  # 离心率平方
        # 使用SciPy的ellipe函数计算第二类完全椭圆积分
        return 4 * a * ellipe(e_sq)
    elif method == 'ramanujan':
        # 拉马努金近似公式
        h = ((a - b) / (a + b))**2  # 椭圆形状参数
        return np.pi * (a + b) * (1 + 3*h / (10 + np.sqrt(4 - 3*h)))
    else:
        raise ValueError("方法参数必须是 'exact' 或 'ramanujan'")

# 示例计算
a, b = 5, 3  # 半长轴和半短轴

# 精确计算
exact_perimeter = ellipse_perimeter(a, b, method='exact')
print(f"椭圆精确周长: {exact_perimeter:.6f}")

# 拉马努金近似
ramanujan_perimeter = ellipse_perimeter(a, b, method='ramanujan')
print(f"拉马努金近似周长: {ramanujan_perimeter:.6f}")

# 计算误差
error = abs(exact_perimeter - ramanujan_perimeter) / exact_perimeter * 100
print(f"近似误差: {error:.4f}%")

这段代码演示了计算椭圆周长的两种方法：精确方法使用第二类完全椭圆积分，近似方法使用拉马努金公式。通过比较可以看出拉马努金公式的高精度特性。