https://mp.weixin.qq.com/s/ozk-7YFH32vGG3b40_YJSQ
大脑是人类最神秘的器官,其工作方式极其复杂。但人脑终究是由很多个神经元细胞构成,就像电脑是由很多个最基础的电子元器件组成。 要探索人脑究竟是如何运转的,需要先了解每一个神经元细胞如何工作。
本文将从数学建模的角度介绍单个神经元细胞的工作方式,并推广至多个神经元细胞构成的神经网络。
一、神经元细胞------工作机理及其数学模型
神经元细胞,有其独特的形态 ,如下图所示:
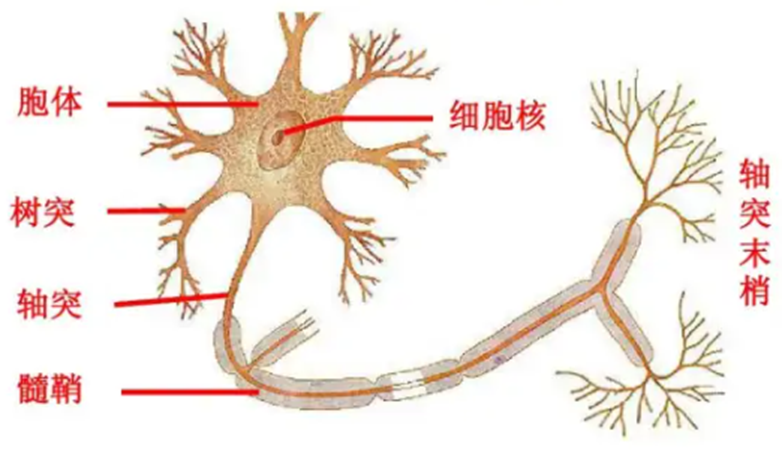
图1.1
神经递质作用于轴突后膜,打开离子通道,让
离子流入后神经元。 离子所到之处,正电荷浓度增加,从而显示出较高的电势。 电势,可以用来刻画一个神经元细胞的状态,以及神经元之间传递信号的能力。
下面建立神经元细胞最基本的模型: 设一个神经元的电势为
,他由从树突收集到的输入信号决定。 n 个输入信号分别为 ,此神经元的电势由这些输入线性决定,即。 一个神经元细胞的输出由其本身的状态决定,设为 。其中
是一个非线性函数,不妨称其为"输出函数"。
将这个模型简化,可得到如下示意图。
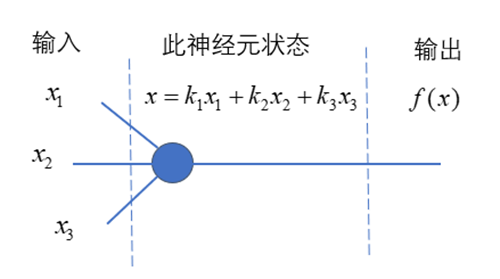
图1.2
思考:
为何取输出函数
为非线性函数,而输入均为线性? 能否将二者都取非线性函数?
二、感受机制------神经网络
末端神经元受到的刺激要传到大脑里,不是一个神经元细胞就能完成的。通常需要很多个神经元首尾相接,层层传递。 由于末端需要很多神经元来收集信号,因此每一层需要若干个神经元细胞。如下图所示
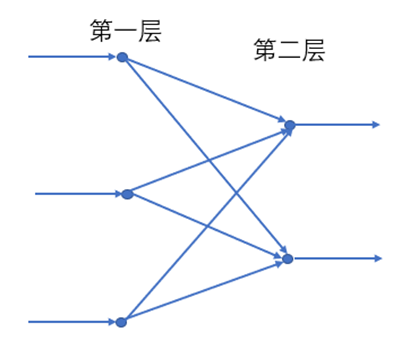
图2.1
多层神经元细胞相互连接,构成一个网络,称为 神经网络。
图中第 i 层的第 j 个神经元的状态记作
, 。第 i 层的第 j 个神经元细胞接收的第 k 个信号源(预先排好顺序,而不是根据接收信号的时间先后顺序)的输入系数记作
。
例如在上图中,第 2 层第 1 个神经元细胞接收到的来自第 1 层的信号为
获得此状态后再以
为输出传递给下一层神经元。
三、神经网络在人工智能中的应用
自从计算机问世以来,人类一直在探索用电脑代替人脑来思考。人工智能,就是人如此探索的产物。 在模拟人的思考方式时,有一类问题很是麻烦:非线性分类。
线性分类是比较简单的,比如将人按年龄分为"年轻"、"年长"两类,可以设置一个界限(例如 40 岁)。超过这个界限为"年长",不足为"年轻"。但非线性分类就很麻烦:如果在下图中画出一条分界线,将红点和蓝点分开,这条线将十分不规则。这种分界线并非直线、平面等规则图形的分类问题,就是非线性分类。
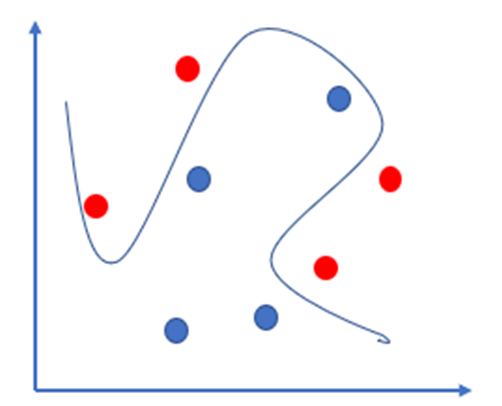
应用背景补充:
非线性分类在人工智能中应用十分广泛。比如很常见的人脸识别:
计算机将扫描到的人脸特征转化为数据。多种原因导致人在识别时的相貌与登记数据时的相貌略有不同。 人脸识别的原理在于将扫描到的相貌数据与计算机认识(即已储存相貌数据)的人做对比,哪个最相似,就确认为哪个人。
也就是说,每一个人的相貌对应的数据集合相当于一个"类",计算机要将输入的相貌数据处理后输出一个分类。
比如张三和李四两个人长得比较像,那么计算机需要在这两个人的相貌之间找到一个边界。实践验证表明,这个边界通常是非线性的。 如果采用的算法不够好,那么计算机就有可能把张三认成李四。
在计算机算法中引人神经网络能够胜任这个任务。
考虑一个简单的非线性分类案例:异或运算(曾在本公众号文章《尼姆博弈》中介绍)
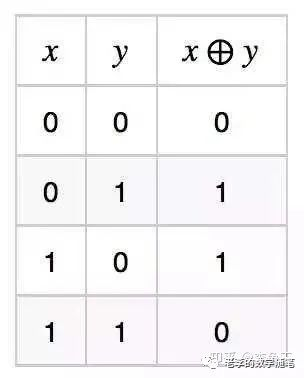
图3.2
采用类似图3.1的方式可画出如下图:
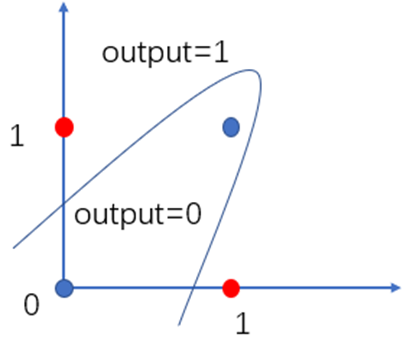
图3.3
为了解决这个问题,采用如下结构的神经网络:
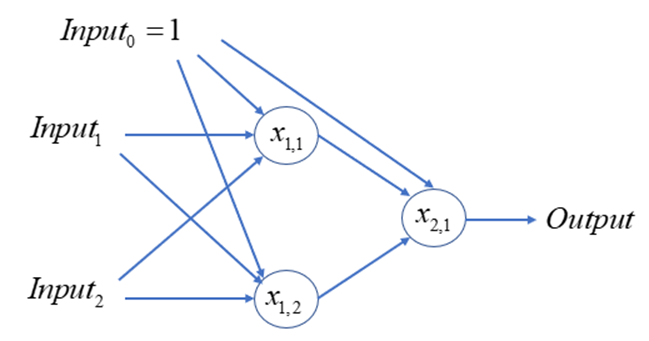
图3.4
其中
为三个神经元的状态。 两个输入信号 的取值范围如图3.2所示。 除此以外还有一个恒定输入
。 取各个神经元的输出函数(在人工智能中称为"激活函数")为半符号函数,即
若取各个输入系数为
,,
,则可满足异或运算的功能。 (这并不是唯一答案,只是不等式组的其中一个解。有兴趣的同学可以自行探索这种输入系数的取法是如何得到的,以及找到更多的解。)
四、联想记忆机制------Hopfield 神经网络
回到人脑。 前两节所述的神经网络有一个局限:信号的传递并不是在若干个神经元细胞之间任意传递。这种结构虽然能够模拟触觉等从末梢到中枢单向传递的感觉机制,但并不能模拟大脑内部的功能。
比如联想记忆,可以从"同位角相等"联想到"两条直线平行",反之也可以从两条直线平行联想到同位角相等。
背景补充:
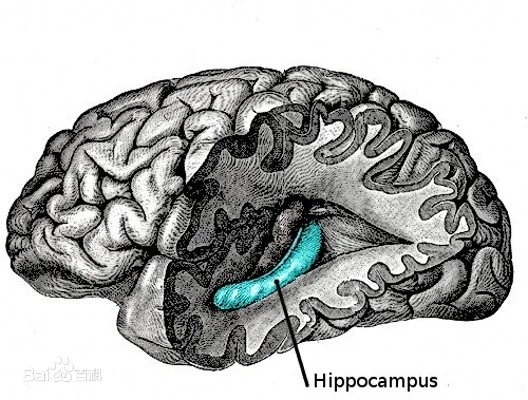
人脑中掌管记忆的部分是"海马体",得名于其形状像海马。
(上图中这个区域并不像海马。事实上,人们首先研究的是猴子、狗等动物脑部的相关区域。这些动物脑中的记忆区域形状像海马)
这种每个神经元之间都有信息传递渠道的网络,称为 Hopfield 神经网络,其结构如下图所示。
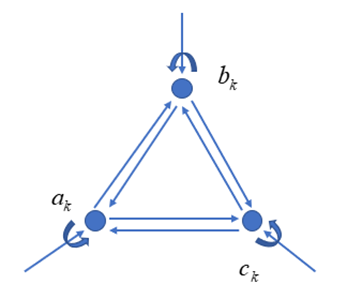
图4.1
为了方便计算,将时间取离散的值。在这种条件下,每个神经元的状态是一个数列,即上图中
。 就神经元 a 而言,其在每一时刻的状态 受上一时刻 的影响,同时也受这一时刻外界输入
的影响。 同样假设这些影响都是线性的, 可以列出如下关系式。
在上式中,输入系数的含义是两个神经元之间的 连接强度。比如是否能从"四点共圆"这个条件很快地联想到相应的角相等。有的同学可能一下子就能想到,这表明存储这两个信息的神经元之间连接强度很强;但对于多年没接触数学的人来说,可能想半天才想起来,甚至想不起来,这表明连接强度很弱。
思考:连接强度如何随时间变化而变化?
经过一定时间的遗忘,连接强度会逐渐削弱。而每一次回忆,连接强度又会增强。 请同学们自行尝试建立数学模型描述这种规律。