好的,我们接下来进入第八单元,是关于低噪声放大器设计的一个简化版介绍。复杂版本的内容我们以后有时间再探讨,这部分我们先不录。
噪声类型
首先,我们来了解一下噪声有哪些主要类型。

噪声主要可以分为两大类:高频噪声 和低频噪声,这两部分是需要重点理解的。
- 高频噪声
这部分,主要分两种:热噪声和散粒噪声。
这两种噪声的频谱都很宽,所以在高频电路里影响特别大。- 第一种是 热噪声(Thermal noise) ,也叫约翰逊噪声或奈奎斯特噪声。顾名思义,它是由晶格的热振动产生的。在金属或半导体中,晶格会持续不规则地振动。同时,内部有电子在移动,这些电子在移动过程中可能会与振动的晶格发生碰撞。温度越高,晶格振动越剧烈,电子撞上的几率就越高,由此产生的随机波动噪声也就越大。
- 散粒噪声(shot noise)不一样,它是因为电流不是连续的水流,而是一个个电子随机通过PN结这样的势垒。就像雨滴打在屋顶上,"啪嗒、啪嗒"声音不规律。电流越大,这种"电子雨滴"的噪声就越明显。
这里注意的是,虽然我们说它们是"高频噪声",但它们的噪声谱本身是平坦的------就是说在各个频率上噪声功率都差不多。那为什么高频电路里它们影响更大呢?因为晶体管在高频时增益会下降 ,信号弱了,噪声相对就显得更大了。
所以做高频电路,特别是LNA(低噪声放大器),一定要处理好这两种噪声。
- 低频噪声 :
- 低频噪声通常称为 闪烁噪声 ,也叫 1/f 噪声。它主要与器件表面或界面状态有关。
- 以MOSFET为例,电子在沟道(例如从源极流向漏极)中运动时,会撞击到半导体与氧化层之间的界面(表面)。这种撞击可能导致界面态捕获或释放电子,这个过程相对缓慢,因此产生的噪声频率成分集中在低频段。
所以,器件的表面积或界面越大,这种噪声通常就越严重。例如,在MOSFET或某些结型器件中,这个问题比较明显。 - 但是,像双极型晶体管(BJT)这种结构则有所不同。以NPN型为例,电子从发射极射出,垂直穿越很薄的基区到达集电极。这个过程中,载流子主要是在体内运动,与表面的相互作用非常少。因此,BJT的闪烁噪声通常很低。现代技术还可以通过设计保护环等措施进一步抑制它,使其噪声性能可能比MOSFET更好。
- 那么,谁会担心低频噪声呢?对于数字电路,低频噪声影响不大。但对于模拟电路,比如振荡器,由于晶体管是非线性器件,低频噪声会通过调制等机制上变频到工作频率附近,造成相位噪声等问题。这种噪声的特点是,频率越低,其噪声功率密度越大,通常与频率成反比关系(1/f^n,n可能为1、2、3或更高),因此被称为"1/f噪声"。
所以,在设计振荡器时,需要特别注意晶体管的非线性特性。这个非线性成分会将其他的噪声频率调制到载波信号的附近。这就是为什么设计振荡器的主要任务之一,就是想办法压低噪声性能 ,特别是中心频率附近的相位噪声 。这些旁边的噪声就是由于非线性造成的频率调制。
当然,一个可行的研究方向就是设法抑制晶体管本身的非线性,从而获得更好的噪声性能,这对于从事射频电路研究的人来说是一个值得考虑的方向。
那么,基于这个原理,我们来思考一个问题:如果要设计一个振荡器,你会选择使用FET 还是BJT ?你更希望器件的高频噪声低 ,还是低频噪声低 ?
对于振荡器来说,显然是BJT 更优。因为BJT的闪烁噪声(1/f噪声)非常低,这对于抑制相位噪声至关重要。
所以,高性能的振荡器设计通常都会选择BJT或者HBT来实现,效果最好。
当然,有些应用为了成本考虑,必须使用CMOS工艺。但用CMOS做出来的振荡器,其相位噪声性能通常会差很多。不过,对于像蓝牙 这类对相位噪声容忍度较高、规格要求较松的应用,CMOS还是可以接受的。但如果是像微波点对点通信 这类要求苛刻的应用,最好还是用BJT或相关工艺来实现。这主要是在规格和成本之间进行取舍。
那对于低噪声放大器呢?我们讲了半天,用哪种器件比较好?
BJT的高频噪声 性能相对较差(但近年来技术改进后也还不错,处于可接受的中等水平),而FET的低频噪声 又比较大。
综合来看,HBT做出来的性能有时反而相当不错,是可以接受的方案。
噪声系数
好了,了解了这些背景,我们来简要介绍一下最后要测量的核心指标------噪声系数 。噪声系数,也叫噪声因数 ,一般用 F 表示。
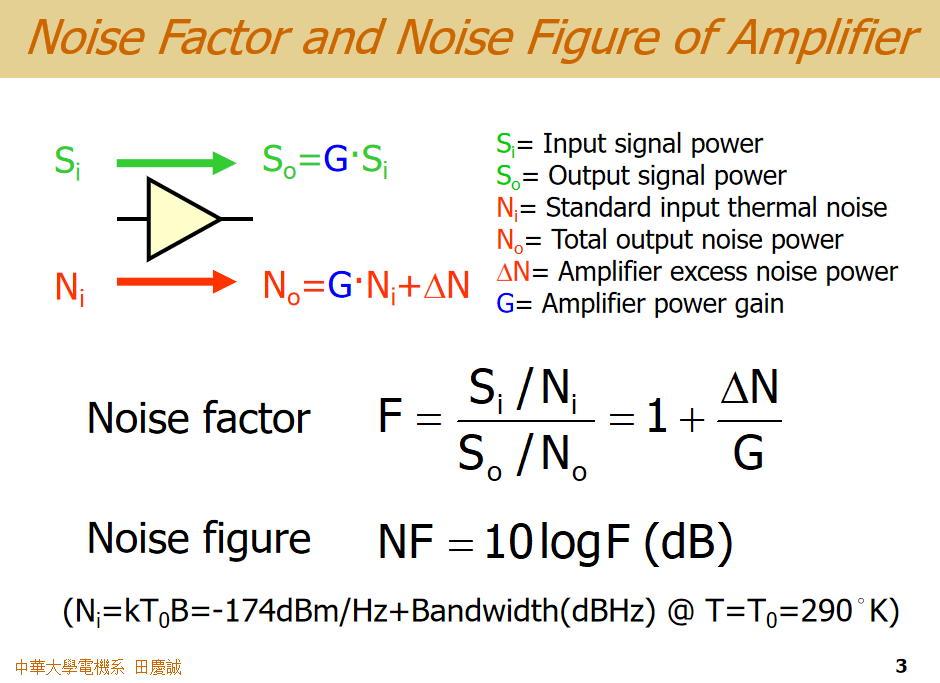
那**噪声系数(Noise factor)和 噪声指数(Noise figure)**有什么区别呢?
噪声指数其实就是把噪声系数取 10*log₁₀ 得到的(注意是10log,不是20log,因为下面定义中涉及的都是功率之比.20log用于电压比,而功率比一定是用10log
我们来看一下定义。假设一个放大器:
- 输入信号功率为 Si。
- 放大器的功率增益为 G。
- 那么,输出的信号功率就是 G × Si(在线性标度下是相乘,换算成dB则是相加)。
同时,我们送入一个标准噪声 源进行测量,这非常重要。这个标准噪声的功率谱密度是 k∗T₀k*T_₀k∗T₀。其中,k是玻尔兹曼常数,T₀是标准温度(290K),k∗T₀k*T_₀k∗T₀计算出来是一个常数,即 -174 dBm/Hz 。
为什么要"每赫兹"呢?因为噪声功率与带宽相关 ,kT₀代表的是单位带宽(1Hz)内的噪声功率。
这个标准噪声 Ni*经过理想放大器后,输出应该只有G×NiG × N_iG×Ni。但实际放大器内部会产生额外的噪声功率 ,记作 ΔN 。
所以,总输出噪声是G×Ni+ΔNG × N_i + ΔNG×Ni+ΔN。
噪声系数就是用来量化这个"额外噪声"有多严重的。它的定义是:输入信噪比 与输出信噪比 的比值。
请问大家,分子大还是分母大?输出信噪比和输入信噪比,哪个更差?
经过一个实际放大器后,信噪比一定是变差的 。因为放大器在放大信号的同时,也增加了额外的噪声(ΔN),使得噪声相对于信号更显著了。所以,输出信噪比一定小于输入信噪比。
因此,我们把 (输入信噪比 / 输出信噪比) 定义为噪声系数 F 。它代表了信噪比恶化了多少倍。再将这个倍数取10log₁₀,就得到了以dB为单位的噪声指数 NF 。
根据公式推导(将Si、So、Ni、NoS_i、S_o、N_i、N_oSi、So、Ni、No的表达式代入信噪比公式),可以得到噪声系数 F 的表达式:(恒大于等于1)
F=1+ΔNG×NiF = 1 + \frac{ΔN}{G × N_i}F=1+G×NiΔN
这里的"1"代表什么意思呢?它对应理想情况,即ΔN = 0,输出信噪比与输入信噪比相同 ,放大器不引入额外噪声。但现实中不存在这样的放大器,总会有额外噪声。
所以,实际噪声系数就是"1"加上一个多余项。这个多余项就是 放大器内部产生的额外噪声功率 与 经放大器放大的标准输入噪声功率 的比值。这清楚地表明了放大器自身噪声的贡献。
那公式中这一项ΔNG×Ni\frac{ΔN}{G × N_i}G×NiΔN代表什么呢?
- G × Ni 是理想的输出噪声功率,即放大器自身不产生噪声时,输入噪声被放大后的结果。
- ΔN 则是放大器内部额外产生的噪声功率。
所以,这一项衡量的就是 "多出来的噪声" 相对于 "理想的输出噪声" 的比例。
大家在推导这个公式时,一定要理解它的物理意义,不要只是机械地计算。通过推导,你会明白为什么要定义噪声系数------就是因为输出信噪比一定会变差 。公式最终表示为 1 + 一项多余项 ,这非常直观。
因此,噪声系数 F 一定是大于或等于 1 的。那么,对应的噪声指数 NF 呢?
- 如果 F = 1(理想情况),则 NF = 10log₁₀(1) = 0 dB。
- 如果 F > 1(实际情况),则 NF > 0 dB。
所以,噪声指数 NF 也是大于等于 0 dB 的,数值越大,代表放大器自身引入的噪声越严重。
关于这个基本概念,还有一种很直观的图形化理解方法,我顺便给大家介绍一下。
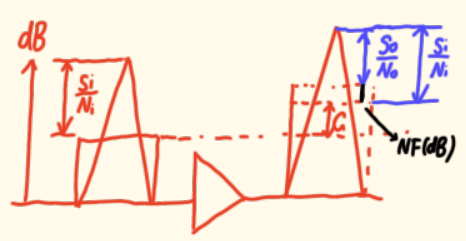
假设我们用 dB 刻度来表示功率。放大器的输入,信号功率在一个电平(图中三角形),噪声功率在另一个较低的电平(图中的矩形),两者之差就是输入信噪比 。
放大器具有增益 G(dB),所以输出信号功率会提升 G dB。理想情况下,输出噪声功率也应该只提升 G dB,这样输出信噪比就和输入信噪比相同。
但实际上,由于放大器内部产生了额外的噪声 ΔN,总输出噪声功率 会比理想值更高,抬升到了一个更高的电平。
这样一来,输出信噪比 就变差了,它等于新的输出信号电平和更高的总输出噪声电平之差。
那么,噪声指数 NF 在图上对应哪一段呢?它就是 输入信噪比(dB值) 与 输出信噪比(dB值) 的差值(图中黑色线段)。
也就是说,输入输出之间信噪比被压缩了多少 dB,这个压缩量就是噪声指数。这样理解就很清楚了。
微波领域的噪声理论
公式
好的,接下来我们要进入微波领域的噪声理论。相关的公式在微波教材中都有,它长成这样

这个公式是怎么来的?它的推导非常复杂,涉及二端口网络理论和晶体管模型,早在上世纪70年代的论文里就已经完成了。我们这里就不重复推导了,现在所有EDA软件(如ADS)都能根据你给的模型直接算出这些参数。
简单来说,对于一个线性二端口网络 (比如我们的晶体管),其噪声性能可以用这个公式来描述。它包含四个关键参数,比如 ΓsΓₛΓs (源反射系数)和 ΓoptΓₒₚₜΓopt (最佳噪声反射系数),以及几个噪声参数(如 Fmin,rnFₘᵢₙ, rₙFmin,rn等)。
这里注意:为什么是四个参数?因为 ΓoptΓ_{opt}Γopt(最佳噪声匹配点) 是一个复数,有实部和虚部(或者说大小和相位),所以Fmin、RnF_{min}、R_nFmin、Rn加上ΓoptΓ_{opt}Γopt的两个分量,一共就是四个。
这个公式以及相关的噪声参数,都与晶体管的小信号模型参数紧密相关。通常,在晶体管的数据手册里,厂家应该提供这四个关键的噪声参数 。有了它们,我们才能进行低噪声设计。
不过,要精确测量这些参数非常困难,也极其昂贵。它对测试环境极其敏感------连接器的损耗、接触压力、甚至环境电磁干扰(比如旁边的Wi-Fi路由器)都会导致测量结果飘忽不定。要想测准,通常需要造价高昂的屏蔽室和专业设备。
所以,对于大多数研发来说,更实际的做法是直接利用芯片厂家或研究机构已经测量并公布的可靠数据。
PS1:
这里的 F 是噪声系数(Noise Factor),是无量纲的线性标度值,不是以dB为单位的噪声指数(Noise Figure)。
PS2:
对于一个晶体管,在特定偏置条件Bias 下,它能达到的最低噪声系数称为 FminF_{min}Fmin 。这是测量或计算得到的。
所有噪声参数(以及S参数)都是偏置依赖的 。不同的偏置点对应不同的小信号模型,进而得到不同的噪声参数。所以,拿到噪声参数表的第一件事,就是确认它是在哪个Vds、Id等偏置条件下测得的,不能乱用。
那么,什么时候能达到这个FminF_{min}Fmin呢?看公式:当源反射系数 Γₛ 等于最佳噪声反射系数 ΓoptΓ_{opt}Γopt 时,公式中后面那一项就为零了,此时 F = FminF_{min}Fmin。非常简单明了。
如果ΓsΓₛΓs不等于ΓoptΓ_{opt}Γopt,噪声系数就会升高。这时我们需要另一个参数:等效噪声电阻 RnR_nRn。它也是测量或推导出来的一个参数。
当然,不要看很复杂,正如前面我们已经提到过,现在所有的主流EDA软件都内置了这个功能:只要你提供了准确的小信号模型,软件就能帮你计算出这些噪声参数。
这时很多同学会问:"老师,既然模型能算,为什么还要费劲去测量呢?"
这个问题问到了关键!模型计算的前提是,模型本身在我们将要使用的偏置区域和频率点是高度准确的 。然而,芯片厂商提供的模型,通常只重点验证和保证了某个常用工作区域 (比如FET的饱和区、BJT的放大区)的直流特性和S参数的准确性。对于其他区域(如截止区、深饱和/深线性区)或像噪声参数这类极其敏感的特性,模型的准确性往往没有经过充分验证 ,很可能不准。
同样,一些非常规用法(比如把晶体管当变容二极管用)更是超出了模型原本的验证范围,模拟结果和实际测试会相差甚远。
所以,模型绝非万能 。它通常只在特定区域可靠,更重要的作用是提供设计趋势参考 和进行原理性仿真 ,帮助我们完成初步的Reference Design。
但要实现最终的、高性能的电路优化,必须依靠工程师的经验和对实际器件特性的深刻理解。软件能带我们走完前三分之一的路,剩下的三分之二,需要我们凭借经验下车,一步步探索和调试才能到达目的地。因此,在射频设计中,经验至关重要。
前置知识
现在,在我们来看看这个噪声公式里的变量之前。先复习一下 ΓsΓₛΓs(源反射系数) 是什么。
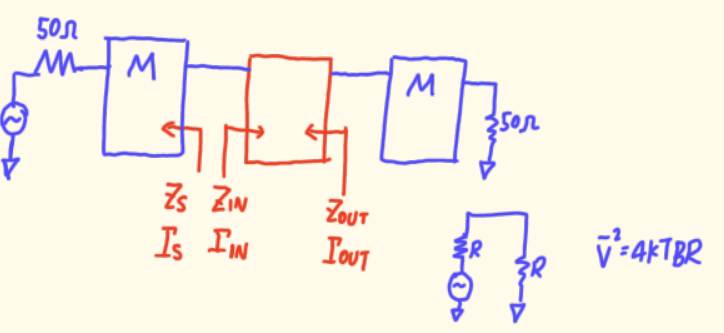
考虑一个晶体管,我们从输入端看进去。实际电路是:信号源(通常内阻为50欧姆)通过一个匹配网络 ,再连接到晶体管。这个"匹配网络+50欧姆源"整体,从晶体管输入端看回去所呈现的阻抗,决定了 ΓsΓₛΓs 。
所以,ΓsΓₛΓs 是一个变量 ,它完全由你设计的这个源端输入匹配网络 决定。当你调整匹配网络的元件时,ΓsΓₛΓs 就会改变。
这时可能会有同学问:"老师,公式里怎么没有体现输出端(负载)的匹配呢?我负载这边也有匹配网络,也是接50欧姆啊。"
这是一个非常好的问题,也是噪声理论的一个关键点:
在二端口网络的噪声系数公式中,噪声系数只与源端的匹配状态(ΓsΓₛΓs)有关,而与负载端的匹配无关。
这是因为我们定义的噪声系数,衡量的是信号从源端进入放大器时,信噪比的恶化程度。这个恶化过程主要发生在放大器的输入端及其内部,负载端的影响(比如它可能影响增益)并不改变放大器自身引入噪声的特性 。当然,负载匹配会影响总增益、稳定性等,但不直接影响 FminFₘᵢₙFmin 等噪声参数本身。这是一个需要理解的重要概念。
另外一个重要概念,我们来思考一下噪声在各级放大器中的影响 。假设晶体管自身会产生噪声(ΔN),前一级产生的噪声进入本级后,会被增益G放大,变得非常大。而后一级产生的噪声虽然也存在,但它不会被本级放大,其功率相对很小。因此,整个系统的噪声性能主要被前级 所主导。
所以,在设计低噪声放大器(LNA)时,第一级 是最关键的。这一级的元件选择,比如电感,如果品质较差、自身电阻较大,就会产生显著的热噪声。
噪声的一个根本来源是电阻。一个电阻R会产生热噪声电压,其均方值公式为 4kTRB 。其中k是玻尔兹曼常数,T是绝对温度,B是带宽。这个4倍的系数是怎么来的呢?我们可以把它等效为一个理想噪声电压源与一个无噪声电阻R串联。
这个噪声源能输出的最大噪声功率是多少?
根据最大功率传输定理,当负载电阻也等于R时,输出功率最大 ,为 kTB 。从这个关系(P = V²/(4R))反推,就可以得到噪声电压的均方值为 4kTRB 。所以,kTB是它能输送的最大噪声功率。
那么,这个噪声会不会被反射呢?会的 。如果源端阻抗不匹配,噪声就会被部分反射回去,无法完全进入放大器。这恰恰就是低噪声设计的关键之一:你可以通过故意调整源端匹配网络(ΓsΓₛΓs) ,使其偏离最大功率传输点(通常意味着失配),来让部分噪声"进不来"。
这样虽然可能牺牲一点增益,但却能有效降低系统的噪声系数(F)。因此,噪声系数与增益(G)是相互关联、需要权衡的。
参数解析
了解了这些前置知识,我们回到核心的噪声系数公式。

- FminF_{min}Fmin (Minimum Noise Factor) : 在源反射系数(ΓsΓₛΓs)等于最佳噪声反射系数(ΓoptΓ_{opt}Γopt)时达到的最小噪声系数(线性值)。
- ΓoptΓ_{opt}Γopt : 使噪声系数达到 FminF_{min}Fmin 时对应的源反射系数,它是一个复数,包含模值和相位(或实部和虚部)。
- rnr_nrn (Equivalent Noise Resistance): 归一化噪声电阻。这是一个关键的参数。
很多人会问:rnr_nrn 是越大越好,还是越小越好?它的物理意义是什么?
我们来看公式:噪声系数 F=Fmin+(rn/Gs)∗∣Γs−Γopt∣2F = F_{min} + (r_n / G_s) * |Γ_s - Γ_{opt}|²F=Fmin+(rn/Gs)∗∣Γs−Γopt∣2
(其中 GsG_sGs 是源电导等导出的归一化因子)
直觉告诉我们,rnr_nrn 越小越好 。为什么?
因为 rnr_nrn直接乘以"失配项" ∣Γs−Γopt∣|Γ_s - Γ_{opt}|∣Γs−Γopt∣²。当你的实际匹配ΓsΓₛΓs偏离最佳点 ΓoptΓ_{opt}Γopt时,噪声系数就会上升。rnr_nrn越大,意味着只要ΓsΓₛΓs稍微偏离ΓoptΓ_{opt}Γopt 一点点,噪声系数就会急剧恶化 。
所以,rnr_nrn的物理意义就是噪声系数对源端失配的"敏感度"或"上升斜率" 。
我们可以用一个三维图来形象理解:
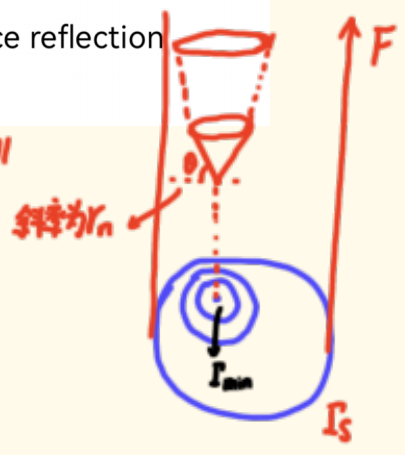
- 水平面是源反射系数ΓsΓₛΓs的复平面(史密斯圆图)。
- 垂直轴是噪声系数 F(或 NF)。
- 这个曲面在ΓsΓₛΓs= ΓoptΓ_{opt}Γopt处有一个"谷底",对应FminF_{min}Fmin。
- 当你从谷底(ΓoptΓ_{opt}Γopt)向任何方向移动(即ΓsΓₛΓs发生失配),噪声系数都会上升。rnr_nrn决定了这个"谷壁"的陡峭程度 。rnr_nrn越大,"谷壁"越陡,系统对匹配误差的容忍度就越差;rnr_nrn越小,"谷"就越平坦,匹配即使有偏差,噪声也不会恶化得太厉害。
安捷伦(是德科技)的仪器界面和很多教科书上都有这种漂亮的噪声系数等高线图。
那么,具体得到这些参数呢?需要使用噪声参数测试系统。通过一个可调的"源调谐器"(Source Tuner)来系统地改变ΓsΓₛΓs,在每一个频率点测量无数个ΓsΓₛΓs下的噪声系数,然后通过算法拟合,就能得到FminF_{min}Fmin、ΓoptΓ_{opt}Γopt和rnr_nrn这四个参数。
实际例子
接下来,我们看一个实际晶体管的噪声参数表(例如 ATF-10136,一个安捷伦的低噪声晶体管)。

观察这些参数随频率变化的趋势:
- FminF_{min}Fmin (或 NF_min) :随着频率升高,噪声系数明显上升。这很容易理解,频率越高,载流子与晶格碰撞的几率越大,热噪声越显著。
- rnr_nrn :这里有一个有趣的现象。在低频段(如4GHz),rnr_nrn值较大;到了高频(如12GHz),rnr_nrn值变小了。这意味着什么?
- 低频时,虽然FminF_{min}Fmin可能较低,但 rnr_nrn很大,噪声系数"谷"非常陡峭。如果你的实际匹配ΓsΓₛΓs因为元件公差、生产变异等原因稍微偏离了设计的最佳点ΓoptΓ_{opt}Γopt,噪声性能就会急剧恶化 ,导致生产良率可能出问题。
- 高频时,尽管FminF_{min}Fmin变差了(谷底升高了),但rnr_nrn变小了,谷变得相对平坦。即使匹配有偏差,性能也不会下降得那么厉害,系统鲁棒性更好。
- 因此,选择晶体管时,不能只看 FminF_{min}Fmin,还要看rnr_nrn 。一个 FminF_{min}Fmin很低但rnr_nrn很大的管子,可能并不适合量产。
此外,我们还会看到 Associated Gain(关联增益) 。它是指在噪声系数达到FminF_{min}Fmin(即 Γ_s = ΓoptΓ_{opt}Γopt)时,放大器所能提供的增益。这个增益通常不是最大可用增益(Gmax) 。因为为了达到最佳噪声匹配(ΓsΓₛΓs = ΓoptΓ_{opt}Γopt),输入端通常是失配的(ΓinΓ_{in}Γin ≠ Γs∗Γₛ^*Γs∗),这会牺牲一部分增益。
因此,在设计中需要在 "最低噪声" 和 "较高增益/良好输入匹配(VSWR)" 之间进行权衡和折衷,这是低噪声放大器设计的核心难点之一。
最后,这些参数还是 偏置依赖(Bias Dependent) 的。我们来看一张 FminF_{min}Fmin随漏极电流 Ids 变化的曲线图。
- 曲线通常呈"U"形。电流太小或太大,FminF_{min}Fmin都会变差,存在一个最优的中间值。
- 这里需要特别警惕一个常见的误解:有些理论或简单模型可能会推导出"噪声系数与功耗成反比"的结论,暗示功率越大噪声越好。这只在很小的信号范围内近似成立。当功率大到晶体管进入强非线性区(如大信号区、压缩区)时,小信号模型和推导公式已经失效,实际情况是噪声会急剧恶化。
- 任何公式和模型都有其适用范围。我们不能把在特定条件下推导出的结论当作普遍真理。当你使用一个公式或模型时,必须清楚它的前提假设和有效区间。这也是工程师经验的价值所在:能够辨别理论的适用边界,并在实践中做出正确的判断和取舍。
好的,我们继续。在晶体管的模型文件中,除了S参数,通常还会提供噪声参数。这些参数会标注其对应的测试偏置点(Bias),使用时必须注意匹配。
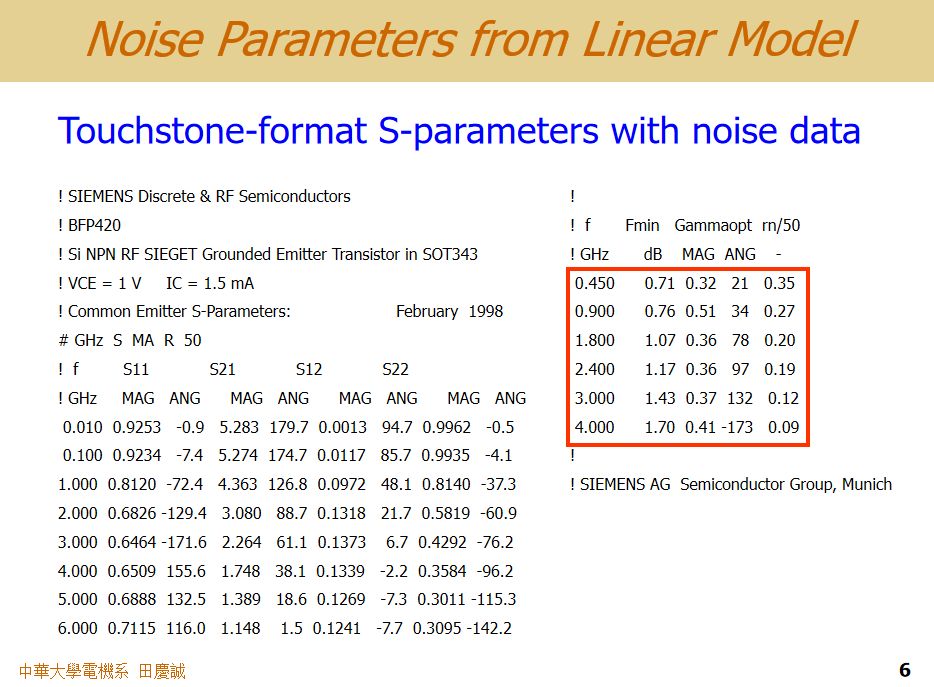
这些噪声参数(如 F_min, Γ_opt)一般以 dB 和角度(或实部/虚部)的形式给出,同时也会给出归一化噪声电阻 R_n。
在设计过程中,当我们确定了晶体管的直流偏置电路后,就可以得到相应的小信号模型(例如,BJT的π模型或FET的小信号等效电路)。利用这个小信号模型,EDA软件(如 ADS、AWR Microwave Office)的噪声分析功能可以计算出噪声参数。你可以在"噪声分析"或"小信号分析"的选项中找到相关设置,输入模型后,软件会自动为你计算Fmin、Γopt和rnF_{min}、Γ_{opt} 和 r_nFmin、Γopt和rn。
但这里必须再次强调:软件基于模型计算出的噪声参数,其绝对精度不一定足够,更多是提供一种趋势参考。最终的优化和确定还需要结合实际测试或更精确的模型数据。
等噪声系数圆
有了噪声系数的理论公式,我们可以推导并在史密斯圆图上绘制出 等噪声系数圆。这个推导过程比较复杂,有兴趣的同学可以查阅参考书。

等噪声系数圆(Constant Noise Figure Circle)的物理意义非常重要:
- 它在源反射系数 ΓsΓ_sΓs 的复平面(即史密斯圆图上)作图。
- 你在这个平面上选择任意一点,都代表你为放大器输入端设计了一个具体的输入匹配网络,使得从晶体管输入端看回去的源阻抗对应那个 Γ_s 值。
- 神奇的是,在同一个圆上的所有点(即无数种不同的源匹配状态),都会产生完全相同的噪声系数 F。
- 这些同心圆的中心点,就是 ΓoptΓ_{opt}Γopt ,对应着最低噪声系数 FminF_{min}Fmin。
- 离中心越远的圆,代表的噪声系数值越大。
要绘制这些圆,你需要输入目标噪声系数 F(或 NF),以及晶体管的四个噪声参数(FminF_{min}Fmin, ΓoptΓ_{opt}Γopt,rnr_nrn)。软件或公式就能计算出对应圆的圆心和半径。
我们来看一张由软件生成的示意图:
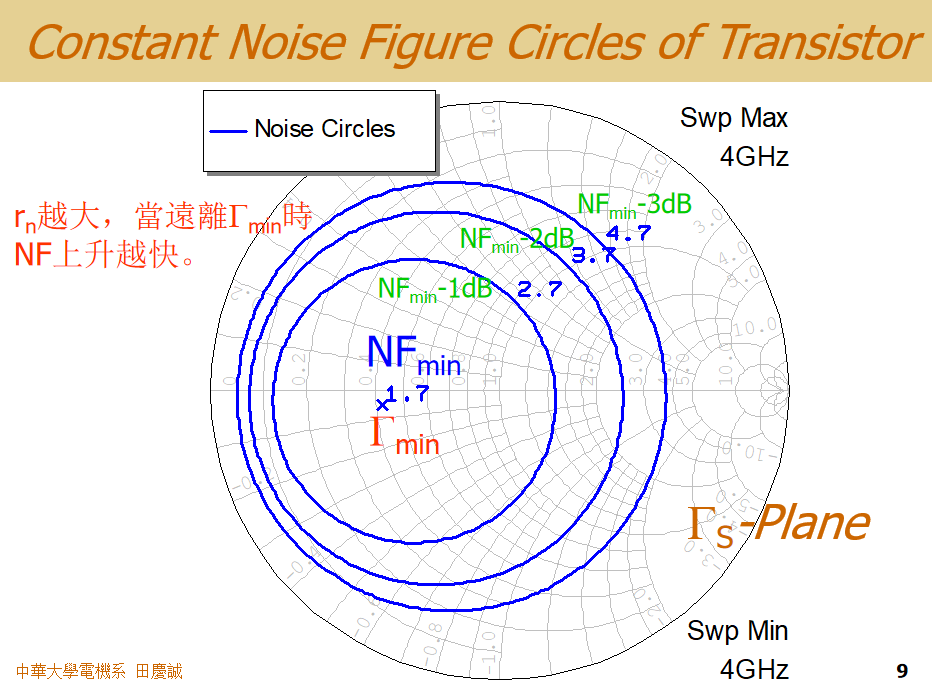
- 中心点就是ΓoptΓ_{opt}Γopt,对应最低噪声指数(例如 1.7 dB)。
- 围绕它的一系列同心圆,分别代表噪声指数增加1 dB、2 dB、3 dB......的等值线。
- rnr_nrn的大小直接影响了这些圆的疏密 。rnr_nrn越大,圆与圆之间的间隔越紧密,这意味着ΓsΓ_{s}Γs只要稍微偏离ΓoptΓ_{opt}Γopt(圆心),噪声系数就会急剧上升("谷壁"很陡)。反之,rnr_nrn小则圆间距大,系统对匹配误差的容忍度更高。
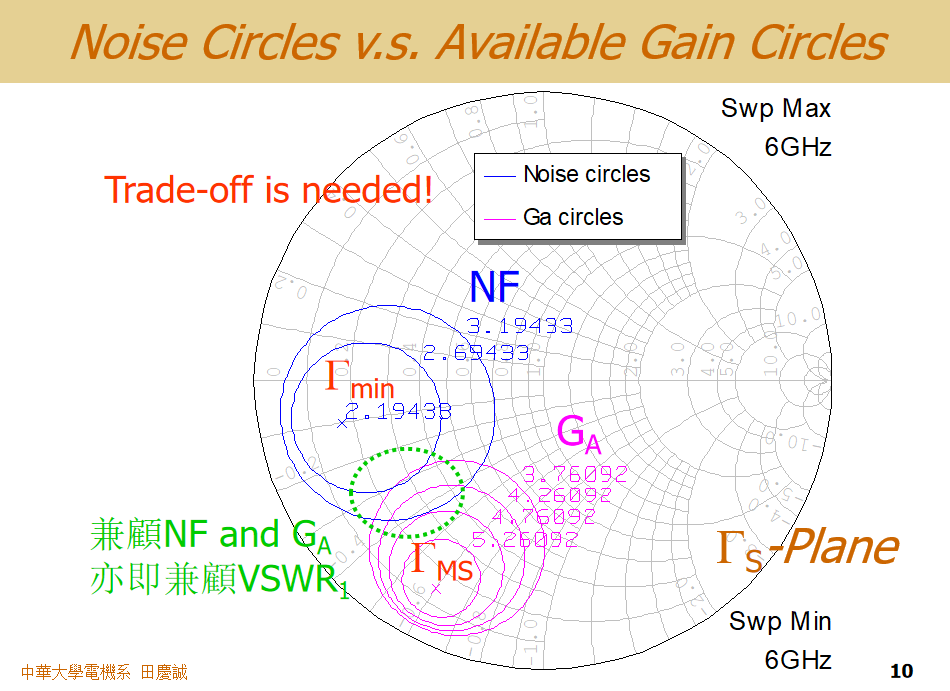
在实际设计低噪声放大器时,我们必须将等噪声系数圆 和 等可用增益圆 放在一起综合考量,即兼顾VSWR1。
什么是等可用增益圆?
- 当放大器的输出端共轭匹配(以获得最大输出功率)时,其增益被称为"可用增益"。
- 这个可用增益与输入端的匹配状态ΓsΓ_{s}Γs密切相关。
- 在史密斯圆图上,也存在一组 等可用增益圆 。圆心通常不是ΓoptΓ_{opt}Γopt,而是另一个点(通常是ΓinΓ_{in}Γin的共轭点附近)。
- 只有当ΓsΓ_{s}Γs等于某一个特定值时,才能同时满足输入输出共轭匹配,此时达到理论上的最大可用增益 GmaxG_{max}Gmax,这在图上通常缩为一点。
- 一旦ΓsΓ_{s}Γs偏离这个最佳增益点,可用增益就会下降。离得越远,增益下降得越多。
这就引出了LNA设计的经典权衡:
观察软件生成的叠加图,你会发现:
- 实现最低噪声的匹配点(ΓoptΓ_{opt}Γopt),和实现最大可用增益的匹配点,几乎从来不重合。
- 如果你将ΓsΓ_{s}Γs设置在ΓoptΓ_{opt}Γopt以获得最低噪声,此时的增益可能会大幅下降(比如从5.7 dB掉到1 dB左右)。
- 反之,如果你追求最大增益,噪声性能就会变差。
因此,设计者需要在 噪声性能(Noise Figure) 和 增益(Gain) 之间找到一个可接受的折衷点。这个点通常位于最低噪声圆和较高增益圆的交汇区域。完美的"最大增益且最低噪声"的晶体管几乎不存在,这正是电路设计的挑战与价值所在。你需要根据系统指标要求,在史密斯圆图上选择一个合适的ΓsΓ_{s}Γs设计值,并据此设计输入匹配网络。
好的,那么在噪声和增益这两个性能指标相互冲突的情况下,我们该怎么办呢?
通常的解决办法是进行折衷(Trade-off) 。我们会在史密斯圆图上,在最低噪声圆(ΓoptΓ_{opt}Γopt附近) 和最大可用增益圆(GmaxG_{max}Gmax点附近) 之间,选择一个合适的中间区域。这个区域能够同时兼顾可接受的噪声性能 和可用的增益。
选择这个区域还有一个好处:它通常也能顾及到输入端的匹配 ,也就是电压驻波比(VSWR)。因为如果ΓsΓ_{s}Γs严重偏离共轭匹配点,VSWR肯定会变差。所以,找到一个折衷点,往往意味着噪声、增益和输入匹配三者达到一个平衡。
感性反馈
那么,有没有办法让这两个天生的"矛盾点"------最佳噪声点(ΓoptΓ_{opt}Γopt)和最大增益点(ΓmsΓ_{ms}Γms)------靠得更近一些呢?这样我们在设计时就会轻松很多。
答案是:有。一个在微波工程领域广为人知的经典技巧就是在晶体管的发射极(或源极)串联一个小电感 ,这被称为 "源极/发射极感性反馈"(Source/Emitter Inductive Feedback)。
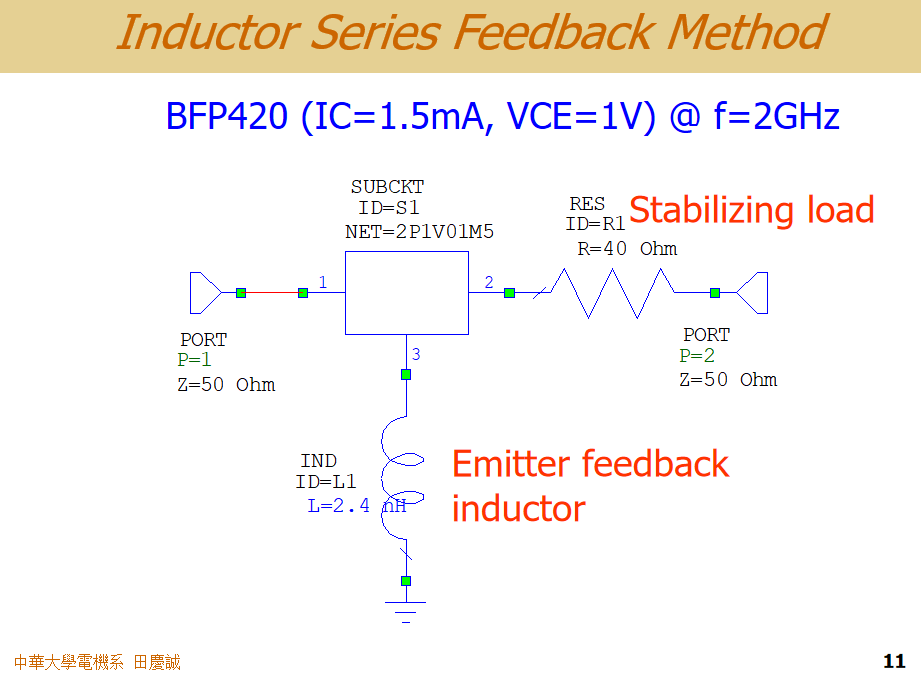
这个技巧的原理很简单:引入一个感性阻抗(jωL),它会同时改变晶体管的输入阻抗和噪声特性,从而影响ΓoptΓ_{opt}Γopt和ΓmsΓ_{ms}Γms在史密斯圆图上的位置。通过精心调整这个电感值,可以使这两个点相互靠近。
当然,这个电感值并非越大越好。需要利用仿真软件去"调谐",找到一个"刚刚好"的值。太大或太小都达不到理想效果。
举个例子:在设计一个低压低电流的放大器时,可能发现其在目标频率(如2GHz)下不稳定。为了稳定放大器,常见的做法是在输出端(负载侧)添加一个稳定电阻 。这里有一个重要原则:对于低噪声放大器(LNA),稳定电阻一律加在输出端。因为如果加在输入端,会直接引入噪声,彻底毁掉噪声性能。相反,对于功率放大器(PA),为了不损耗宝贵的输出功率,稳定电阻则应加在输入端。这是一个典型的设计取舍。
回到感性反馈,我们来看仿真结果:在没有电感(L=0)时,ΓoptΓ_{opt}Γopt和ΓmsΓ_{ms}Γms在圆图上相距甚远。随着我们逐渐增加电感值(例如0.2 nH, 0.4 nH, 0.8 nH...),可以观察到这两个点会沿着特定的轨迹移动。我们的目标就是找到一个电感值,使得这两个点之间的距离最短。例如,可能发现当L=0.8 nH时,两者最接近,达到了较好的折衷。
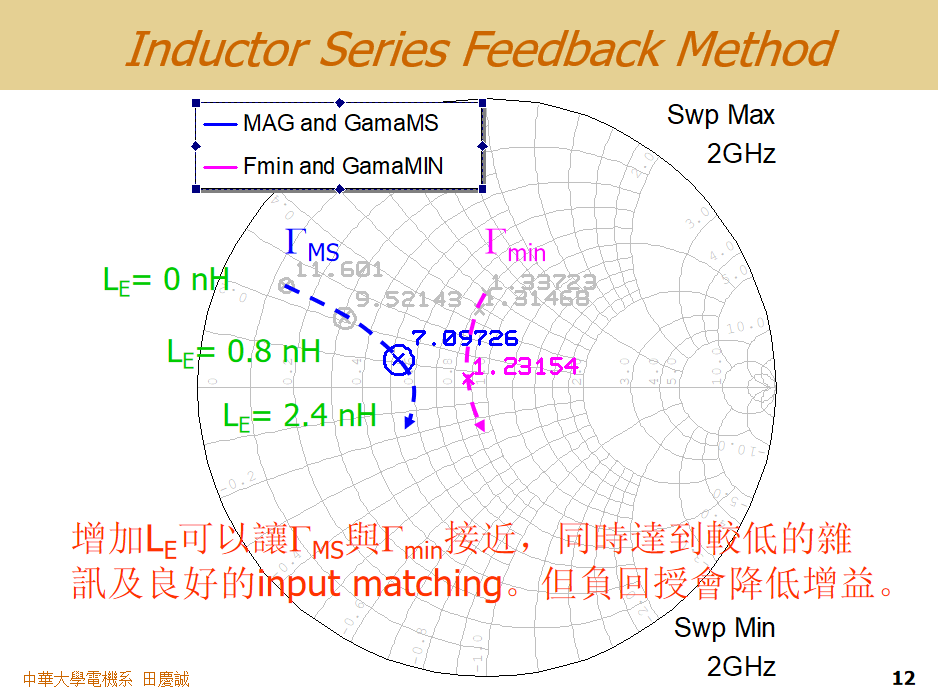
然而,这里又引入了新的权衡:
- 工艺实现:这个电感值通常非常小(可能在1 nH以下)。在标准CMOS或GaAs工艺中,工艺厂提供的最小电感值可能远大于此(例如最小的也有几十pH或更大)。这时就需要设计者自己设计并绘制一个定制化的微型电感(例如用传输线实现),并在流片前进行充分的仿真和验证。直接使用工艺库中的标准电感可能无法满足要求。
- 增益代价 :引入源极电感本质上是引入了负反馈 。负反馈在改善稳定性和调整阻抗的同时,必然会降低增益。从仿真数据可以看到,随着电感值增加,增益(Gain)会从最初的11.6 dB逐渐下降到9.52 dB、7 dB......如果电感加得太大,增益损失会非常严重。因此,你必须在"噪声与增益点的接近程度"和"可接受的增益损失"之间再次进行权衡。
结论 :通过添加一个适当大小的源极/发射极感性反馈,可以有效地使最佳噪声匹配点和最大增益匹配点相互靠近,从而让我们有可能同时实现较低的噪声 、良好的增益 和可接受的输入匹配。
但是,这个过程充满了各种取舍(Trade-offs):
- 电感值大小的取舍(影响点距和增益)。
- 性能与工艺可实现性的取舍。
- 稳定性、噪声、增益、匹配等多个指标间的综合取舍。
剩下的优化工作,就需要各位设计者在仿真软件中仔细探索和调试了,看你们能否为自己的设计找到那个最优的平衡点。这就是射频电路设计的艺术所在。