四大差错校验方法全解析

前言

本文基于《王道计算机网络》一书，梳理了计算机网络中常用的差错校验方法，重点关注位级差错（位错），而不涉及报文或帧级别的错误。值得注意的是，这些校验方法不仅适用于计算机网络，也可广泛应用于串口等各类数据传输场景。

奇偶校验

奇校验：通过调整检验位，使其整条数据中所有"1"的个数(包括校验位)为奇数

偶校验：通过调整检验位，使其整条数据中所有"1"的个数(包括校验位)为偶数

简单来说就是数据位+校验位中1的个数要保持为奇数(奇校验)或偶数(偶校验)。

例如我需要传输一个字节的数据：10110001

其中**"1"的数量为4个**。使用奇校验时，需将校验位设为"1"以使"1"的总数变为奇数；采用偶校验时，应设校验位为"0"以保持"1"的总数为偶数。

如图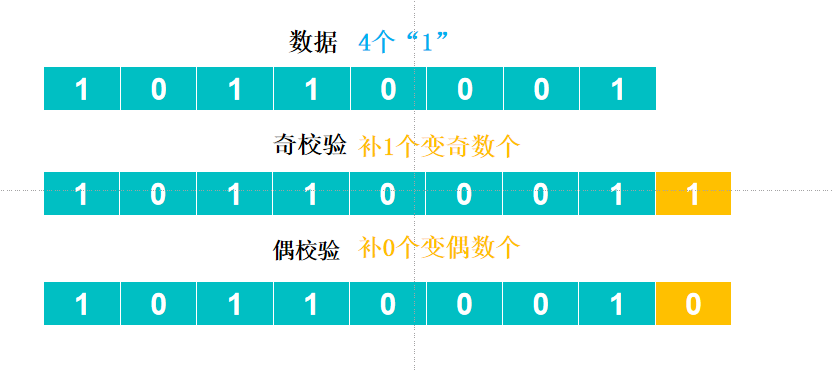

优势之处

方法简单，容易实现，计算开销特别小

不足之处

该机制仅能检测部分错误，例如单比特错误。当出现双比特错误时（实际上应指偶数个比特错误），检错功能会失效。不过由于数据错误本身是小概率事件，同时发生多个比特错误的概率更低，因此通常只讨论单比特和双比特的情况。此外，该机制无法定位错误的具体位置，也不具备纠错能力。

应用场景

奇偶校验的缺陷在于其检测能力有限且不具备纠错功能。因此，这种校验方式通常应用于对数据可靠性要求较低的场景，或是短距离、干扰小的环境。

串行通信：如UART协议，RS232，RS485等

网络协议：在数据链路层或者一些其他对数据可靠性要求不高的场合中常用

循环冗余校验(CRC校验)

CRC（Cyclic Redundancy Check）是一种基于多项式计算的校验算法，广泛应用于数据通信和存储中检测数据传输或存储时的错误。其核心思想是将数据视为一个二进制多项式，通过模2除法生成校验码。

基本原理

CRC校验通过对数据位串进行多项式模2除法运算，生成固定长度的校验码（余数）。发送方将校验码附加到原始数据后传输，接收方用相同算法重新计算校验码并与接收到的校验码对比，判断数据是否出错。

步骤

选择一个生成多项式 .多项式最高次数项的次数记为。通常为固定标准，如CRC-16、CRC-32等。多项式决定了校验的位数和性能。
将原始数据左移（补零）位/位 ，为生成多项式位数减1(多项式的最高项次数）。例如，CRC-16生成多项式为16位，需补15个0。
用补零后的数据作为被除数，生成多项式作为除数，进行模2除法（按位异或操作）。除法过程忽略借位，每一步仅需判断当前最高位是否为1。

举例说明

当前有一个数据M=101001，计算其循环冗余码。

首先选择多项式：即
将数据位后面加0，共3个(最高项次数为3/多项式位数为4，4-1=3）
通过模2运算得出余数R为001，该值即为循环冗余校验码R=FCS=001

注：该图来自2026王道计算机网络 59页

M+R组成一个带有CRC功能的数据，接收方可以用收到的数据进行模2除法，得到余数为0则数据无误。

需要注意的是，虽然理论上存在误码但余数为0的可能性，但这种概率极低。因此我们通常认为：当余数为0时数据正确，余数不为0则数据必然存在错误。

优势方面

CRC校验能够有效检测单比特、双比特、奇数位及突发错误。它具有计算效率高、硬件实现简单的特点，特别适合实时系统应用。其校验强度取决于所选生成多项式。由于可以完全通过硬件实现，CRC的校验码添加和数据提取速度非常快。

不足之处

CRC校验码相对较长。虽然在某些特殊情况下具备1比特纠错能力，但多数情况下仍无法纠正错误。若采用纯软件实现，其计算开销相对较大。

校验和

校验和是一种用于检测数据传输或存储过程中错误的技术。其核心思想是通过对原始数据执行特定计算，生成一个简短的校验值。接收方重新计算校验值并与发送方的校验值比对，若不一致则说明数据可能出错。

校验和是一种通过较短校验码验证长数据完整性的方法。我们以8位校验为例进行说明（实际应用中通常使用16位或32位校验）。

举例说明

示例数据为3字节：10011010 10100011 10101011

将数据划分为固定大小的块（此处每块8位）
将所有分块数据进行二进制相加
对求和结果取反即得到校验和

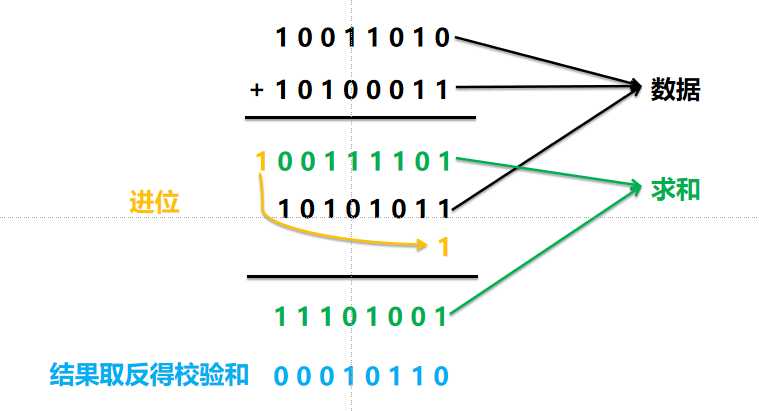
如图所示，校验和为00010110 。接收端在获取数据及校验和后，可将两者相加，若结果为全1则数据正确，否则表明存在传输错误。

需要说明的是，实际应用中通常采用16位校验和，校验数据的长度范围一般为几十字节至数万字节。此处仅为演示用途，但基本原理和方法相同。

优势方面

实现简单：校验和的软硬件实现都非常便捷
高效验证：可用少量校验数据检验大量原始数据

典型应用场景

网络协议：如TCP/IP协议栈中的UDP和TCP协议均采用校验和机制

海明码

海明码简介

海明码（Hamming Code）是一种用于检测和纠正单比特错误的线性纠错码，由理查德·海明（Richard Hamming）于1950年提出。其核心思想是通过添加冗余校验位，在数据传输或存储过程中实现错误定位与修正。

海明码原理

海明码的校验位数量由数据位长度决定，满足关系：

其中：

为数据位
为检验位

海明码编码步骤

1. 确定校验位数量

假设数据位为 1011 （），则需满足，解得，总位数。

2. 确定校验位位置

检验位在海明位号为的位置上

复制代码

海明位号: 1  2  3  4  5  6  7 
值:       _  _  1  _  0  1  1 
         P1 P2 D1 P3 D2 D3 D4

3. 分组

确定每个校验位覆盖特定位置的比特。分组条件：数据位的海明号=检验该数据位的检验位的海明号的和。

例如：数据位对应的海明位号为3；检验位号的海明位号为1，的海明位号为2；3=1+2则数据位的检验位号为

同理的检验位号为；的检验位号为；的检验位号为；

以此我们确定了每个检验位覆盖的数据位为：

注：在这个过程中我们可以清楚的感受到我们上一步确认校验位位置的绝妙之处，其实我们发现校验位所在的海明位号的组合可以代表所有数据位的位置。

4. 计算校验位

检验位的值=本身覆盖的数据位的值求异或

对于数据 1011：

最终编码：0110011

海明码解码与纠错

1. 计算综合征（Syndrome）

接收方重新计算校验位并与接收的校验位比较，通过异或得到错误位置。

综合征表示无错误。

若接收数据为 0110001（第6位错误）：

综合征（十进制6），表示错误在位置6。

纠错的实现原理用文字描述可能不够直观，但细心的读者已经注意到：海明码的校验位实际上采用的是偶校验方式。关键在于每个数据位都受到多个校验位的交叉验证，这些校验关系的组合具有唯一性，使得错误定位成为可能。

理解这个交叉验证机制时，图形展示确实比文字说明更直观。这里不得不赞叹王道教材对该知识点的讲解既精准又生动。因此我再次借鉴了王道PPT中的图解来说明这个原理。

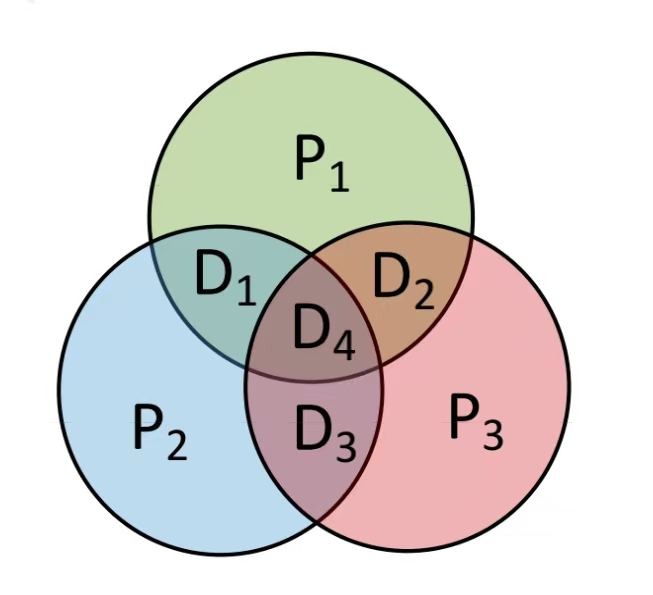
从图中我们可以看到每一个大圈都代表一个S，当其中一个数据位出现错误时，至少会影响到2个S，通过3个S的关系，我们可以锁定出错的数据位。

优势方面

纠错能力强

海明码能够检测并纠正单比特错误，对于双比特错误也能检测。这种能力使其在传输或存储过程中对抗噪声干扰时表现优异。例如，在内存（如ECC内存）中，海明码可以纠正因硬件故障或宇宙射线导致的单比特翻转。

编码效率较高

相比简单的奇偶校验码，海明码在冗余与纠错能力之间取得了较好的平衡。其冗余比特数量与数据比特长度的对数成正比，公式如下：冗余比特数 ( r ) 满足 ( 2^r \geq k + r + 1 )，其中 ( k ) 为数据比特长度。对于较长的数据块，海明码的冗余开销相对较低。

实现简单

海明码的编码和解码可以通过硬件或软件高效实现。编码时通过异或运算生成校验位，解码时通过计算综合征（syndrome）快速定位错误位置。

不足之处

法纠正多比特错误

标准海明码仅能纠正单比特错误。若发生两比特或更多比特错误，可能无法正确纠错，甚至可能误判。

冗余开销随数据增长

虽然海明码的冗余比特较少，但对于极短的数据块（如4比特数据需3比特校验位），冗余比例较高。数据长度与校验位的关系是非线性的，可能导致某些场景下效率不足。

扩展性有限

海明码的纠错能力难以直接扩展到多比特纠错。若需更高容错能力（如纠正双比特错误），需使用更复杂的编码（如BCH码或Reed-Solomon码），这会显著增加计算复杂度和冗余。

应用场景

内存错误检测（ECC内存）
通信数据传输（如卫星通信）
存储系统（RAID、硬盘纠错）

海明码的优势在于高效的单比特纠错能力，但无法处理多比特错误。如需更高容错，可扩展为SEC-DED（单错纠正双错检测）码。