小试牛刀-基于几何要素分辨insar升降轨道数据

🔍 背景与挑战

在日常遥感数据处理中，我们经常遇到这样的挑战：如何从海量的SAR影像图幅覆盖矢量文件中，快速准确地识别出升降轨道信息？

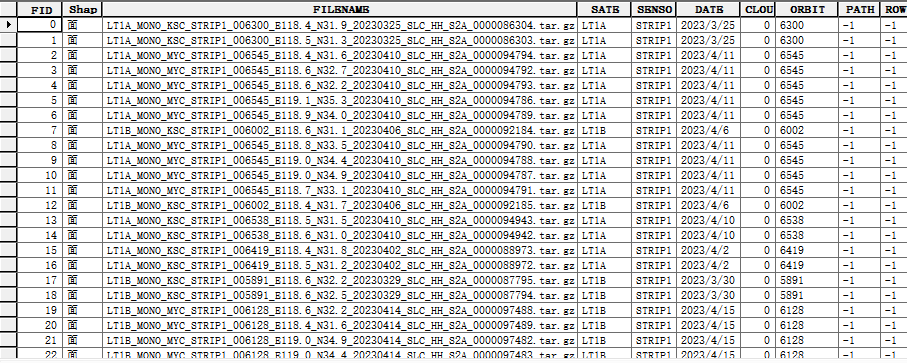
最近我收到这样一个需求：现有5000多个SAR影像的图幅覆盖矢量文件，但属性信息几乎无用（如下图所示）。如何仅通过图幅的矢量几何信息来区分升降轨道？这确实是个让人头疼的问题！

💡 关键发现：方位角的秘密

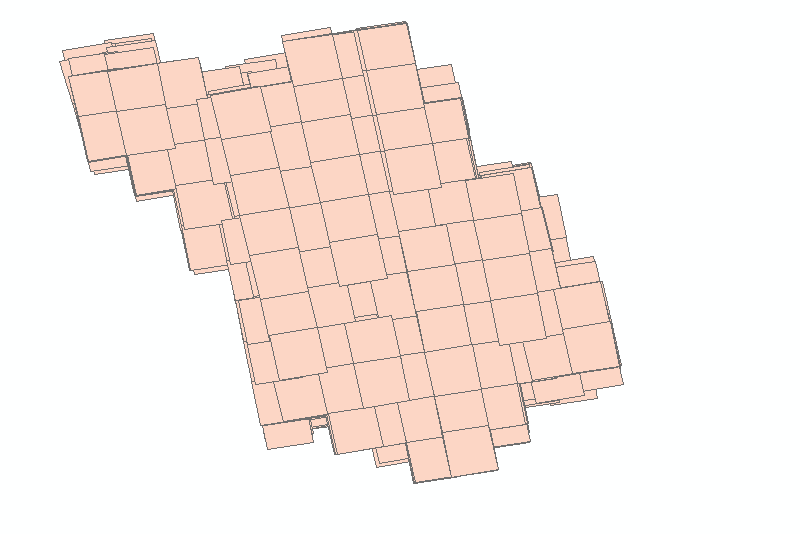
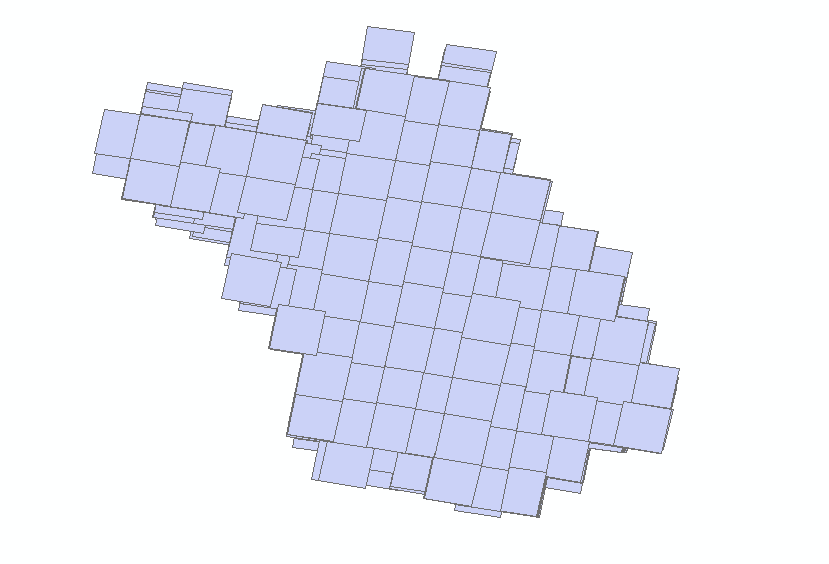
仔细观察矢量图幅后，我发现了升降轨道数据的一个关键区别：

从上图可以明显看出，升轨数据和降轨数据在图幅的倾斜方向上存在明显差异。这个发现让问题变得简单了！

🎯 解决方案：基于几何特征的自动化判别

核心思路
提取矩形边框：每个图幅矢量都是一个矩形
识别南北走向的边：找出矩形中代表卫星飞行方向的一边
计算斜率：通过边的斜率判断航向角的正负
自动分类：根据斜率正负自动标记升降轨道

📊 代码逻辑解析

1. 关键步骤说明

步骤1：获取矩形顶点

python 复制代码

for point in row[1].getPart(0):
    points.append([point.X, point.Y])

从几何对象中提取所有顶点坐标

步骤2：按X坐标排序

python 复制代码

points_sorted_by_x = sorted(points, key=lambda p: p[0])

按X坐标升序排列，最左边的点在前

步骤3：选取最左边的两个点

python 复制代码

if points_sorted_by_x[0] == points_sorted_by_x[1]: 
    min_x_point1 = points_sorted_by_x[1]
    min_x_point2 = points_sorted_by_x[2]

处理可能的重复顶点（多边形闭合时的首尾相同点）

步骤4：计算斜率并判断

python 复制代码

slope = (y2 - y1) / (x2 - x1)
if slope > 0:
    row[2] = "2"  # 降轨
else:
    row[2] = "1"  # 升轨

正斜率 → 线向右上方倾斜 → 降轨

负斜率 → 线向右下方倾斜 → 升轨

2. 数学原理

斜率公式：slope = ΔY / ΔX = (y2 - y1) / (x2 - x1)

地理意义：

当卫星由北向南飞行（降轨）时，轨迹线向右上方倾斜，斜率为正

当卫星由南向北飞行（升轨）时，轨迹线向右下方倾斜，斜率为负

3. 完整脚本

python 复制代码

import arcpy
... mapdoc = arcpy.mapping.MapDocument("CURRENT")  # 获取地图文档
... lyr = arcpy.mapping.ListLayers(mapdoc)[0]
... cursor = arcpy.da.UpdateCursor(lyr, ["OID@", "SHAPE@", "升降轨"])
... for row in cursor:
...     points=[]
...     for point in row[1].getPart(0):
...         points.append([point.X, point.Y])
...     points_sorted_by_x=sorted(points,key=lambda p:p[0])
...     if points_sorted_by_x[0] ==points_sorted_by_x[1]: 
...         min_x_point1 = points_sorted_by_x[1]
...         min_x_point2 = points_sorted_by_x[2]
...     else:
...         min_x_point1 = points_sorted_by_x[0]
...         min_x_point2 = points_sorted_by_x[1]
...     x1, y1 = min_x_point1
...     x2, y2 = min_x_point2
...     slope = (y2 - y1) / (x2 - x1)  # 计算斜率
...     if slope > 0:
...         row[2]="2"
...     else:
...         row[2]="1"
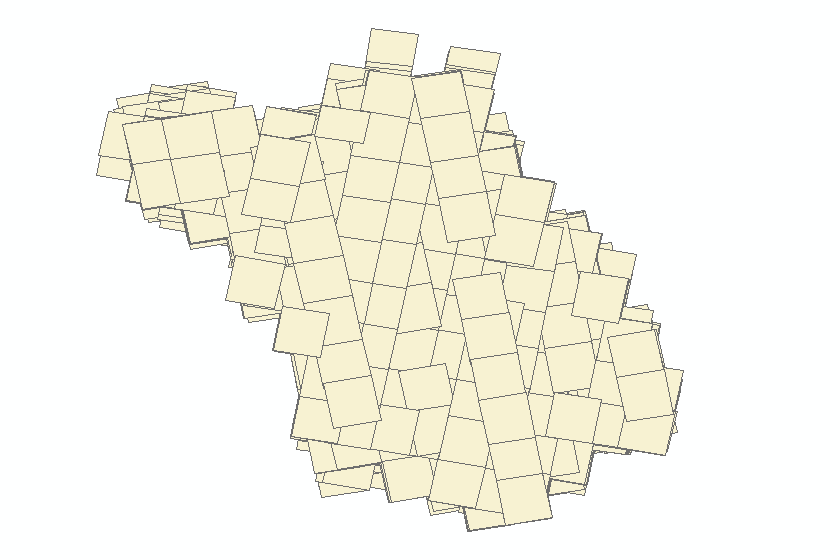
...     cursor.updateRow(row)

🖥️ 效果展示

运行上述脚本后，矢量文件中的"升降轨"字段被自动填充，可以通过符号化显示，直观查看分类效果：：