【深度拆解 Qwen3-Next】Gated DeltaNet 线性注意力的实现与优化

文章目录

• 前言
• 一、模型结构
• [二、init 函数 + 算子统计](#二、init 函数 + 算子统计)
• [三、forward 函数](#三、forward 函数)
• • [3.1 算子 - causal_conv1d_update - 增量更新卷积（推理模式）](#3.1 算子 - causal_conv1d_update - 增量更新卷积（推理模式）)
  • [3.2 算子 - causal_conv1d_fn - 全序列因果卷积（训练模式）](#3.2 算子 - causal_conv1d_fn - 全序列因果卷积（训练模式）)
  • [3.3 causal_conv1d_fn 和 causal_conv1d_update 的区别总结](#3.3 causal_conv1d_fn 和 causal_conv1d_update 的区别总结)
  • [3.4 算子 - chunk_gated_delta_rule](#3.4 算子 - chunk_gated_delta_rule)
  • • [3.4.1 代码](#3.4.1 代码)
    • [3.4.2 总体功能概览](#3.4.2 总体功能概览)
    • [3.4.3 源码逐行分析](#3.4.3 源码逐行分析)
    • [3.4.4 两个 mask 矩阵](#3.4.4 两个 mask 矩阵)
    • [3.4.5 chunk 的并行技术](#3.4.5 chunk 的并行技术)
    • [3.4.6 chunk 的并行技术原理解析](#3.4.6 chunk 的并行技术原理解析)
    • [3.4.7 总结：](#3.4.7 总结：)
  • [3.5 算子 - fused_recurrent_gated_delta_rule](#3.5 算子 - fused_recurrent_gated_delta_rule)
• 参考

前言

本文将深入解析 Qwen-3-next 模型中 class Qwen3NextGatedDeltaNet 的实现机制，该代码位于 GitHub 上的 transformers 项目。

源码路径：src/transformers/models/qwen3_next/modeling_qwen3_next.py

---

在 Transformer / 注意力机制代码中，(B, L, H, D) 是 HuggingFace 等多数 Transformer 层的输出格式

在 HuggingFace Transformers、绝大多数标准 Multi-Head Attention 实现里：

(Batch, Sequence_length, Num_heads, Head_dim)

也就是：

维度	含义
B	batch size
L	序列长度（token 数）
H	head 个数
D	每个 head 的特征维度

这是 Transformer encoder/decoder 层中最常用的形状。

一、模型结构

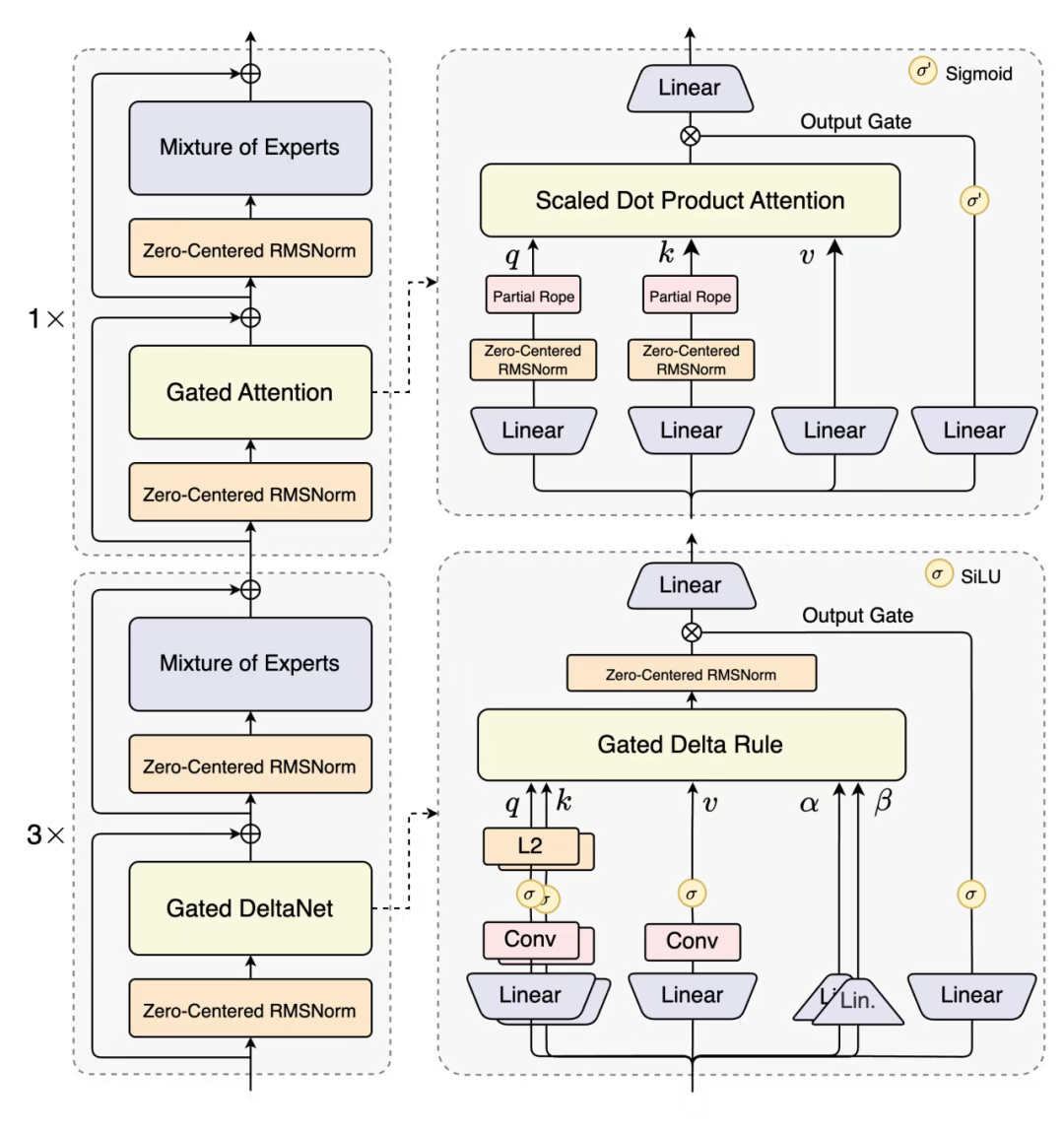
• 75% 采用 Gated DeltaNet（线性注意力）技术：轻松处理 32K、64K 乃至 256K 的超长文本，速度极快且内存占用仅呈线性增长 ，彻底解决"文本越长越卡顿"的问题。

• 25% 运用原创的 Gated Attention（门控注意力）机制：精准捕捉关键信息，**确保模型"重点记忆"**能力，避免在长文本处理过程中丢失重要内容 。（可以参考【Qwen 团队 NeurIPS 2025 重磅成果】门控注意力为何能革新大模型架构？）

二、init 函数 + 算子统计

输入 hidden_states 线性投影得到 Q \mathbf{Q} Q K \mathbf{K} K V \mathbf{V} V Z \mathbf{Z} Z α \mathbf{\alpha} α β \mathbf{\beta} β

class Qwen3NextGatedDeltaNet(nn.Module):
    def __init__(self, config: Qwen3NextConfig, layer_idx: int):
        super().__init__()
        self.hidden_size = config.hidden_size
        self.num_v_heads = config.linear_num_value_heads
        self.num_k_heads = config.linear_num_key_heads
        self.head_k_dim = config.linear_key_head_dim
        self.head_v_dim = config.linear_value_head_dim
        self.key_dim = self.head_k_dim * self.num_k_heads
        self.value_dim = self.head_v_dim * self.num_v_heads

        self.conv_kernel_size = config.linear_conv_kernel_dim
        self.layer_idx = layer_idx
        self.activation = config.hidden_act
        self.act = ACT2FN[config.hidden_act]
        self.layer_norm_epsilon = config.rms_norm_eps

        # QKV
        self.conv_dim = self.key_dim * 2 + self.value_dim
        # 因果卷积
        self.conv1d = nn.Conv1d(
            in_channels=self.conv_dim,
            out_channels=self.conv_dim,
            bias=False,
            kernel_size=self.conv_kernel_size,
            groups=self.conv_dim,
            padding=self.conv_kernel_size - 1,
        )

        # projection of the input hidden states
        # qkvz - [b, s, key_dim * 2 + value_dim * 2]
        projection_size_qkvz = self.key_dim * 2 + self.value_dim * 2
        # ba - [b, s, num_v_heads * 2]
        projection_size_ba = self.num_v_heads * 2
        
        self.in_proj_qkvz = nn.Linear(self.hidden_size, projection_size_qkvz, bias=False)
        self.in_proj_ba = nn.Linear(self.hidden_size, projection_size_ba, bias=False)

        # time step projection (discretization)
        # instantiate once and copy inv_dt in init_weights of PretrainedModel
        self.dt_bias = nn.Parameter(torch.ones(self.num_v_heads))

        A = torch.empty(self.num_v_heads).uniform_(0, 16)
        self.A_log = nn.Parameter(torch.log(A))
			
		
        self.norm = (
            Qwen3NextRMSNormGated(self.head_v_dim, eps=self.layer_norm_epsilon)
            if FusedRMSNormGated is None
            else FusedRMSNormGated(
                self.head_v_dim,
                eps=self.layer_norm_epsilon,
                activation=self.activation,
                device=torch.cuda.current_device(),
                dtype=config.dtype if config.dtype is not None else torch.get_default_dtype(),
            )
        )

        self.out_proj = nn.Linear(self.value_dim, self.hidden_size, bias=False)
        
		# 算子 - causal_conv1d_fn 
        self.causal_conv1d_fn = causal_conv1d_fn
        # 算子 - causal_conv1d_update
        self.causal_conv1d_update = causal_conv1d_update or torch_causal_conv1d_update
        # 算子 - chunk_gated_delta_rule
        self.chunk_gated_delta_rule = chunk_gated_delta_rule or torch_chunk_gated_delta_rule
        # 算子 - fused_recurrent_gated_delta_rule
        self.recurrent_gated_delta_rule = fused_recurrent_gated_delta_rule or torch_recurrent_gated_delta_rule

序号	注释中的算子名称	对应代码变量 / 函数	说明
1	causal_conv1d_fn	self.causal_conv1d_fn	CUDA/CPU fused causal conv1d 函数，用于 chunk 推理
2	causal_conv1d_update	self.causal_conv1d_update	用于增量推理（incremental decoding）的 causal conv1d 状态更新（state update）
3	chunk_gated_delta_rule	self.chunk_gated_delta_rule	chunk 维度上的增量 gating + delta rule 计算，用于一次处理多个 token
4	fused_recurrent_gated_delta_rule	self.recurrent_gated_delta_rule	fused recurrent 形式的 gated delta rule，用于 token-by-token 推理（纯增量）

关于双版本算子的使用说明 ：

1、优先使用高性能版本（编译版本）

• 示例算子： causal_conv1d_update 、 chunk_gated_delta_rule 、 fused_recurrent_gated_delta_rule
• 特性： 基于 flash-linear-attention（FLA）的 Triton/CUDA 编译算子 优势：
  • 运行速度更快
  • 内存占用更低
  • 延迟更小
• 适用场景：正式训练/推理环境

2、备选方案：PyTorch 参考版本

• 示例算子： torch_causal_conv1d_update 、torch_chunk_gated_delta_rule、 torch_recurrent_gated_delta_rule
• 特性： 纯 PyTorch 实现（慢速回退方案） 特点：
  • 保持计算逻辑完全一致
  • 执行效率较低（缺乏并行优化）
• 适用场景：
  • CPU 环境
  • 不支持 Triton 的环境
  • 调试环境

3、实现策略总结： 系统提供两套实现方案

• 高性能 Triton/CUDA 内核
• PyTorch 参考实现 运行时自动选择：优先采用高性能版本，若不可用则回退至 PyTorch 版本。两个版本保持严格的计算等价性，仅存在性能差异。

三、forward 函数

    def forward(
        self,
        hidden_states: torch.Tensor,
        cache_params: Optional[Qwen3NextDynamicCache] = None,
        cache_position: Optional[torch.LongTensor] = None,
        attention_mask: Optional[torch.Tensor] = None,
    ):
        hidden_states = apply_mask_to_padding_states(hidden_states, attention_mask)

        # Set up dimensions for reshapes later
        batch_size, seq_len, _ = hidden_states.shape

        use_precomputed_states = (
            cache_params is not None
            and cache_params.has_previous_state
            and seq_len == 1
            and cache_position is not None
        )

        # getting projected states from cache if it exists
        if cache_params is not None:
            conv_state = cache_params.conv_states[self.layer_idx]
            recurrent_state = cache_params.recurrent_states[self.layer_idx]

apply_mask_to_padding_states 函数说明：

该函数用于将 padding token 对应的隐藏状态置零，有效防止这些填充标记在后续的线性递归或卷积运算中产生干扰。若不进行清零处理，这些填充标记的隐藏状态会参与卷积/递归/线性计算，导致模型状态受到污染。通过清零操作，可以确保这些填充标记被视为"无效标记"。

该函数解决了 Mamba 类模型中已知的问题（issue #66）。

        projected_states_qkvz = self.in_proj_qkvz(hidden_states)
        projected_states_ba = self.in_proj_ba(hidden_states)
        query, key, value, z, b, a = self.fix_query_key_value_ordering(projected_states_qkvz, projected_states_ba)
        query, key, value = (x.reshape(x.shape[0], x.shape[1], -1) for x in (query, key, value))

这段代码首先通过线性变换将 hidden_states 投影为混合向量，随后使用 fix_query_key_value_ordering 将其分解为 Q/K/V/Z 和门控参数 b/a，最终将 Q/K/V 展平为单头维度以供后续计算使用。

fix_query_key_value_ordering 函数：

该函数负责将模型混合投影输出的向量序列重新组织，拆分为结构化的多头 Q、K、V、Z 矩阵及其对应的门控参数 b 和 a，以便后续进行注意力机制和线性递归计算。

        mixed_qkv = torch.cat((query, key, value), dim=-1)
        mixed_qkv = mixed_qkv.transpose(1, 2)

        if use_precomputed_states:
            # 2. Convolution sequence transformation
            # NOTE: the conv state is updated in `causal_conv1d_update`
            mixed_qkv = self.causal_conv1d_update(
                mixed_qkv,
                conv_state,
                self.conv1d.weight.squeeze(1),
                self.conv1d.bias,
                self.activation,
            )
        else:
            if cache_params is not None:
                conv_state = F.pad(mixed_qkv, (self.conv_kernel_size - mixed_qkv.shape[-1], 0))
                cache_params.conv_states[self.layer_idx] = conv_state
            if self.causal_conv1d_fn is not None:
                mixed_qkv = self.causal_conv1d_fn(
                    x=mixed_qkv,
                    weight=self.conv1d.weight.squeeze(1),
                    bias=self.conv1d.bias,
                    activation=self.activation,
                    seq_idx=None,
                )
            else:
                mixed_qkv = F.silu(self.conv1d(mixed_qkv)[:, :, :seq_len])

        mixed_qkv = mixed_qkv.transpose(1, 2)

该代码通过拼接 Q/K/V 并应用深度因果卷积（causal depthwise conv1d）实现时序特征变换，同时支持两种处理模式：

• 推理时增量更新（causal_conv1d_update）
• 训练时整序列处理（causal_conv1d_fn）

作为 Qwen3-Next 的核心设计，该方法用线性卷积替代了部分注意力机制的混合功能。具体实现步骤如下：

1. Q/K/V 拼接
   输入维度：

query: [b, s, key_dim]
key:   [b, s, key_dim]
value: [b, s, value_dim]

拼接后维度变为：

mixed_qkv: [b, s, key_dim*2 + value_dim]

2. 维度转换
   为适配 Conv1d 输入格式 [b, channels, seq_len]，将 mixed_qkv 转换为：

[b, c, s] 其中 c = key_dim*2 + value_dim

3. 卷积处理
   根据场景采用不同处理方式：

• （A）推理模式 ：使用增量状态更新（详见 3.1 节 causal_conv1d_update）
• （B）训练模式 / 全序列模式 ：（详见 3.2 节 causal_conv1d_fn）
  • 存储 conv_state（用于推理缓存）
  • 使用 fused CUDA 版本的 causal conv
  • 退化方案：PyTorch 普通卷积 + SiLU

模式	使用的算子	场景
训练 / 全序列推理	causal_conv1d_fn	一次处理整个序列
增量推理（token by token）	causal_conv1d_update	推理，每次只处理新 token

4. 输出转换
   最终将结果转回原始格式 [b, s, c]

---

3.1 和 3.2 节中的算子高性能实现代码源自：causal-conv1d 库

3.1 算子 - causal_conv1d_update - 增量更新卷积（推理模式）

torch_causal_conv1d_update

在现代大模型（LLM）如 Qwen3-next、Llama3、GPT-4.x 的架构设计中，卷积（Convolution）正在重新登场 。与传统 ResNet 中的大卷积不同，LLM 中的卷积更轻量、更局部、更高效，目的是补足 Transformer 的局部建模能力，并进一步提升推理速度。

def torch_causal_conv1d_update(
    hidden_states,
    conv_state,
    weight,
    bias=None,
    activation=None,
):
    _, hidden_size, seq_len = hidden_states.shape
    state_len = conv_state.shape[-1]

    hidden_states_new = torch.cat([conv_state, hidden_states], dim=-1).to(weight.dtype)
    conv_state.copy_(hidden_states_new[:, :, -state_len:])
    out = F.conv1d(hidden_states_new, weight.unsqueeze(1), bias, padding=0, groups=hidden_size)
    out = F.silu(out[:, :, -seq_len:])
    out = out.to(hidden_states.dtype)
    return out

简单讲，这段函数实现了：一种可用于增量推理（逐 token 推理）的因果卷积更新机制。

普通卷积需要一次性处理整个序列；而增量推理要求：

• 输入 token 是逐步到来的
• 不能重复计算整个历史
• 必须保证"因果性"（不能看到未来）

因此需要一个专门的机制将卷积的历史状态保存下来 ，这就是： conv_state（卷积缓存）

通过它，模型在生成每一个 token 时仅需计算一次卷积，而不必扫描全部历史。

---

① 获取输入维度

_, hidden_size, seq_len = hidden_states.shape
state_len = conv_state.shape[-1]

• hidden_states: 当前步新输入的 tokens 的隐层表示
• conv_state: 卷积需要的历史缓存（长度 = 卷积核大小 - 1）

② 拼接历史 + 新输入

hidden_states_new = torch.cat([conv_state, hidden_states], dim=-1)

卷积核若大小为 K，那么当前要卷积的位置必须能看到： 当前 token、前 K-1 个历史 token，这些历史内容由 conv_state 提供，因此必须拼接。

③ 更新 conv_state（关键）

conv_state.copy_(hidden_states_new[:, :, -state_len:])

这一步保证： 下次卷积时能继续使用这次序列的"尾部"、conv_state 长度固定，不会随序列增长，最终让卷积推理的复杂度变成 O(1)。

④ 执行 depthwise 1D 卷积

out = F.conv1d(
    hidden_states_new,
    weight.unsqueeze(1),
    bias,
    padding=0,
    groups=hidden_size,
)

这是 逐通道卷积（depthwise convolution）： 每个 channel 单独卷积、更轻量、更快、更适合局部特征提取。

⑤ 只保留当前输入对应的输出

out = out[:, :, -seq_len:]

在拼接了 conv_state + hidden_states 后卷积会产生更长的输出，但仅最后一段是我们需要的。

⑥ 激活 + dtype 转换

out = F.silu(out)
out = out.to(hidden_states.dtype)

---

动图式理解：因果卷积如何滑动？

下面用 ASCII 演示一个 kernel size=4 的因果卷积是如何滑动的：

Step 1：输入 t1

窗口: [?,?,?,t1] → out1

前 3 个位置由 conv_state 提供。

Step 2：输入 t2

窗口: [?,?,t1,t2] → out2

Step 3：输入 t3

窗口: [?,t1,t2,t3] → out3

Step 4：输入 t4

窗口: [t1,t2,t3,t4] → out4

卷积窗口完全铺满，能正常滑动。

Step 5：输入 t5

窗口: [t2,t3,t4,t5] → out5

每次滑动 1 格。 conv_state 保存了窗口的前 K-1 个位置。

这就是增量卷积的精髓：无需重复计算整个序列，只需依赖短暂的卷积状态。

---

Qwen3-next 为什么要引入卷积？

总结成 5 个核心原因：

① Transformer 在局部模式建模上有弱点，卷积可以补强

Attention 对长距离依赖很强，但对局部结构不够敏感。

卷积的专长就是：提取局部模式、利用固定大小的感受野、识别移动不变的结构，因此两者非常互补。

② 卷积比注意力更便宜（O(n) vs O(n²)）

在高效模型中（如 Qwen3、RWKV、Hyena），卷积都是提升吞吐与速度的利器。

③ 卷积具备"平移不变性"

即：不论模式出现在哪里，卷积都能识别出来。

这特别适用于 NLP 中的：固定短语、Byte-level pattern、边界相关模式。

④ 卷积增强 token-to-token 信息流

Transformer 的 MLP 层是 逐 token 运算（pointwise），看不到邻居 token。

加入卷积后：MLP → 具备局部感知能力的 MLP。训练更稳定，表现更好。

⑤ 卷积非常适合增量推理（Streaming）

只需要保存：KV Cache（注意力历史）、Conv Cache（卷积历史）。

即可做到：每生成一个 token，都只计算 O(1) 成本。

这正是 Qwen3-next 推理能如此高效的原因。

---

3.2 算子 - causal_conv1d_fn - 全序列因果卷积（训练模式）

高性能版本的简要介绍

1. 输入格式

x: [batch_size, channels, sequence_length]
weight: [channels, kernel_size]
bias: [channels] 或 None
activation: 可调用激活函数（如 SiLU）
seq_idx: None 或用于分块的序列索引

2. 输出格式

输出张量: [batch_size, channels, sequence_length]

3. 核心原理（类似标准卷积，但严格保持时序因果性）

以 kernel_size = 3 为例：

输出 y[t] 的计算公式：

y[t] = weight[0] * x[t] + weight[1] * x[t-1] + weight[2] * x[t-2]

关键说明：

• 当 t-1 < 0 时，输入值视为 0
• 深度可分离：每个通道使用独立的卷积核
• 因果性约束：禁止使用未来时刻的输入 x[t+1]

核心特性：

卷积窗口严格限制在过去时间方向

这正是"因果卷积(causal conv)"的本质特征。

4. 功能优势

• 训练时可对整个序列执行高效并行卷积
• 通过 CUDA 融合内核实现加速
• 支持基于分块的流式处理

3.3 causal_conv1d_fn 和 causal_conv1d_update 的区别总结

特性	causal_conv1d_fn	causal_conv1d_update
输入	整个序列 x[b,c,s]	单 token x[b,c,1]
输出	整个卷积结果	当前 token 的卷积输出
速度	训练时最快（CUDA fused）	推理时最快（O(1) update）
状态	不需要	需要维护 conv_state
用途	训练 / 批量推理	增量推理（LLM decode）

它们是 同一个数学操作的两个优化实现。

causal_conv1d_fn ：一次性对整条序列做因果卷积（训练用），实现 depthwise causal 1D convolution 的全序列并行形式 。
causal_conv1d_update ：像 RNN 一样只更新下一步卷积结果（推理用），实现该卷积的递推形式，使推理复杂度从 O(nk) 降至 O(k)。

---

继续 forward 函数：

        query, key, value = torch.split(
            mixed_qkv,
            [
                self.key_dim,
                self.key_dim,
                self.value_dim,
            ],
            dim=-1,
        )
        # query.shape = [B, T, num_k_heads, head_k_dim]
		# key.shape   = [B, T, num_k_heads, head_k_dim]
		# value.shape = [B, T, num_v_heads, head_v_dim]
		# B = batch T = token 个数（模型看到的序列长度）注意：这里的 T 遵循因果性约束
        query = query.reshape(query.shape[0], query.shape[1], -1, self.head_k_dim)
        key = key.reshape(key.shape[0], key.shape[1], -1, self.head_k_dim)
        value = value.reshape(value.shape[0], value.shape[1], -1, self.head_v_dim)

        beta = b.sigmoid()
        # If the model is loaded in fp16, without the .float() here, A might be -inf
        g = -self.A_log.float().exp() * F.softplus(a.float() + self.dt_bias)
 		...

这段代码从 QKV 的线性投影结果中分离出 query/key/value，并将 Q/K/V 重塑为多头格式 (num_heads, head_dim)，支持 K-head 和 V-head 数量不一致。同时计算 Linear Attention 的核心门控参数 β（gate）和衰减因子 g（decay factor）。

在 Qwen3-Next 的 Attention 状态递推中，数学公式表示为：

S t = α t S t − 1 + β t ( v t − α t S t − 1 k t ) k t ⊤ S_t = \alpha_t S_{t-1} + \beta_t (v_t - \alpha_t S_{t-1}k_t) k_t^\top St=αtSt−1+βt(vt−αtSt−1kt)kt⊤

这是 Gated ΔAttention 的标准形式，具有以下特性：

• 线性计算复杂度（O(T)）
• 可递推性（仅依赖 Sₜ₋₁）
• 保持因果性（无需 causal mask）

参数对应关系：

1. β（门控参数）

对应公式中的 β t \beta_t βt ，代码实现：beta = b.sigmoid()，作为每个时间步 t 的 input gate：

• 控制当前 key/value 信息的加入比例
• β=0 表示完全忽略当前 token
• β=1 表示完全信任当前 KV

2. g（衰减因子）

对应公式中的 α t \alpha_t αt ，代码实现：g = -self.A_log.float().exp() * F.softplus(a.float() + self.dt_bias)，经过exp(-g)处理后得到 α t = e − g t \alpha_t = e^{-g_t} αt=e−gt：

• 控制历史状态 Sₜ₋₁ 的衰减程度
• 决定记忆保留比例
• 由A_log和dt（通过softplus(a + dt_bias)）共同决定连续时间系统的离散化因子

参数对应关系总结：

数学符号	代码变量	功能描述
β t \beta_t βt	beta	输入门控（调节当前token信息吸收量）
α t \alpha_t αt	exp(-g)	衰减因子（控制历史记忆保留程度）

---

继续 forward 函数：

        if not use_precomputed_states:
            core_attn_out, last_recurrent_state = self.chunk_gated_delta_rule(
                query,
                key,
                value,
                g=g,
                beta=beta,
                initial_state=None,
                output_final_state=cache_params is not None,
                use_qk_l2norm_in_kernel=True,
            )

        else:
            core_attn_out, last_recurrent_state = self.recurrent_gated_delta_rule(
                query,
                key,
                value,
                g=g,
                beta=beta,
                initial_state=recurrent_state,
                output_final_state=cache_params is not None,
                use_qk_l2norm_in_kernel=True,
            )

        # Update cache
        if cache_params is not None:
            cache_params.recurrent_states[self.layer_idx] = last_recurrent_state

        z_shape_og = z.shape
        # reshape input data into 2D tensor
        core_attn_out = core_attn_out.reshape(-1, core_attn_out.shape[-1])
        z = z.reshape(-1, z.shape[-1])
        core_attn_out = self.norm(core_attn_out, z)
        core_attn_out = core_attn_out.reshape(z_shape_og)
        core_attn_out = core_attn_out.reshape(core_attn_out.shape[0], core_attn_out.shape[1], -1)

        output = self.out_proj(core_attn_out)
        return output

这段代码的核心计算流程：

1. 调用 ΔAttention 更新规则
   • chunk 模式：整序列处理（训练场景）
   • recurrent 模式：单 token 增量处理（推理场景）
2. 得到线性注意力输出（core_attn_out）和 ΔAttention 状态 Sₜ（缓存用）（last_recurrent_state）
3. 更新 KV 状态缓存（用于文本生成）
4. 对输出执行 Norm（注意力归一化：Qwen3NextRMSNormGated / FusedRMSNormGated）
5. 投影到输出维度（out_proj）

---

在 FLA（flash-linear-attention）框架中，3.4 和 3.5 章节所对应的原始算子实现可在 FLA 库 中找到。

3.4 算子 - chunk_gated_delta_rule

3.4.1 代码

FLA（flash-linear-attention）的 chunk 实现并不是完整的 DeltaAttention，而是 DeltaAttention 的 分块并行化计算的中间步骤。最终归一化是在 Qwen3-Next 的 Attention 层里做的，不在 chunk kernel 内部做。

def torch_chunk_gated_delta_rule(
    query,
    key,
    value,
    g,
    beta,
    chunk_size=64,
    initial_state=None,
    output_final_state=False,
    use_qk_l2norm_in_kernel=False,
):
    initial_dtype = query.dtype
    if use_qk_l2norm_in_kernel:
        query = l2norm(query, dim=-1, eps=1e-6)
        key = l2norm(key, dim=-1, eps=1e-6)
    query, key, value, beta, g = [
        x.transpose(1, 2).contiguous().to(torch.float32) for x in (query, key, value, beta, g)
    ]

    batch_size, num_heads, sequence_length, k_head_dim = key.shape
    v_head_dim = value.shape[-1]
    pad_size = (chunk_size - sequence_length % chunk_size) % chunk_size
    query = F.pad(query, (0, 0, 0, pad_size))
    key = F.pad(key, (0, 0, 0, pad_size))
    value = F.pad(value, (0, 0, 0, pad_size))
    beta = F.pad(beta, (0, pad_size))
    g = F.pad(g, (0, pad_size))
    total_sequence_length = sequence_length + pad_size
    scale = 1 / (query.shape[-1] ** 0.5)
    query = query * scale

    v_beta = value * beta.unsqueeze(-1)
    k_beta = key * beta.unsqueeze(-1)
    # reshape to chunks
    query, key, value, k_beta, v_beta = [
        x.reshape(x.shape[0], x.shape[1], -1, chunk_size, x.shape[-1]) for x in (query, key, value, k_beta, v_beta)
    ]
    g = g.reshape(g.shape[0], g.shape[1], -1, chunk_size)
    mask = torch.triu(torch.ones(chunk_size, chunk_size, dtype=torch.bool, device=query.device), diagonal=0)

    # chunk decay
    g = g.cumsum(dim=-1)
    decay_mask = ((g.unsqueeze(-1) - g.unsqueeze(-2)).tril().exp().float()).tril()
    attn = -((k_beta @ key.transpose(-1, -2)) * decay_mask).masked_fill(mask, 0)
    for i in range(1, chunk_size):
        row = attn[..., i, :i].clone()
        sub = attn[..., :i, :i].clone()
        attn[..., i, :i] = row + (row.unsqueeze(-1) * sub).sum(-2)
    attn = attn + torch.eye(chunk_size, dtype=attn.dtype, device=attn.device)
    value = attn @ v_beta
    k_cumdecay = attn @ (k_beta * g.exp().unsqueeze(-1))
    last_recurrent_state = (
        torch.zeros(batch_size, num_heads, k_head_dim, v_head_dim).to(value)
        if initial_state is None
        else initial_state.to(value)
    )
    core_attn_out = torch.zeros_like(value)
    mask = torch.triu(torch.ones(chunk_size, chunk_size, dtype=torch.bool, device=query.device), diagonal=1)

    # for each chunk
    for i in range(0, total_sequence_length // chunk_size):
        q_i, k_i, v_i = query[:, :, i], key[:, :, i], value[:, :, i]
        attn = (q_i @ k_i.transpose(-1, -2) * decay_mask[:, :, i]).masked_fill_(mask, 0)
        v_prime = (k_cumdecay[:, :, i]) @ last_recurrent_state
        v_new = v_i - v_prime
        attn_inter = (q_i * g[:, :, i, :, None].exp()) @ last_recurrent_state
        core_attn_out[:, :, i] = attn_inter + attn @ v_new
        last_recurrent_state = (
            last_recurrent_state * g[:, :, i, -1, None, None].exp()
            + (k_i * (g[:, :, i, -1, None] - g[:, :, i]).exp()[..., None]).transpose(-1, -2) @ v_new
        )

    if not output_final_state:
        last_recurrent_state = None
    core_attn_out = core_attn_out.reshape(core_attn_out.shape[0], core_attn_out.shape[1], -1, core_attn_out.shape[-1])
    core_attn_out = core_attn_out[:, :, :sequence_length]
    core_attn_out = core_attn_out.transpose(1, 2).contiguous().to(initial_dtype)
    return core_attn_out, last_recurrent_state

3.4.2 总体功能概览

该函数实现了一种分块（chunk）、门控（gated）、delta rule 累积记忆型注意力机制，类似于某些 RNN + Attention 混合结构（如 DeltaNet / RWKV / Gated Delta Networks 家族），通过：

• 将 Q,K,V 分块，减少全局注意力的复杂度
• 添加 g（门控衰减因子）+ β（重要性权重）
• 基于 delta rule 更新递归状态
• 在 chunk 内本地并行，在 chunk 间递归更新状态

最终输出一种高效近似注意力效果。

3.4.3 源码逐行分析

函数签名

def torch_chunk_gated_delta_rule(
    query,
    key,
    value,
    g,
    beta,
    chunk_size=64,
    initial_state=None,
    output_final_state=False,
    use_qk_l2norm_in_kernel=False,
):

定义一个函数，输入 Q,K,V 和门控参数 g, β，并按 chunk 计算 gated delta-rule attention。

数据预处理

    initial_dtype = query.dtype

记录原始 dtype，最后会把输出转换回去。

可选：对 Q/K 做 L2 归一化

    if use_qk_l2norm_in_kernel:
        query = l2norm(query, dim=-1, eps=1e-6)
        key = l2norm(key, dim=-1, eps=1e-6)

如果指定，则将 Q 与 K 每个向量归一化成 unit vector（常用于 Kernelized Attention）。

维度转置成 (B, H, L, D) 并转换为 float32

    query, key, value, beta, g = [
        x.transpose(1, 2).contiguous().to(torch.float32) for x in (query, key, value, beta, g)
    ]

如果原 shape 是 (B, L, H, D)，转换为 (B, H, L, D)。beta,g 也 reshape 成 (B, H, L)。

保存基本形状

    batch_size, num_heads, sequence_length, k_head_dim = key.shape
    v_head_dim = value.shape[-1]

• K 的最后维度就是 key 维度
• V 的最后维度是 value 维度

Padding 使 sequence 能被 chunk_size 整除

    pad_size = (chunk_size - sequence_length % chunk_size) % chunk_size

计算需要 pad 的 token 数。

    query = F.pad(query, (0, 0, 0, pad_size))
    key = F.pad(key, (0, 0, 0, pad_size))
    value = F.pad(value, (0, 0, 0, pad_size))
    beta = F.pad(beta, (0, pad_size))
    g = F.pad(g, (0, pad_size))

后面 reshape 每 chunk 等长时需要 pad，得到实际分块长度。

    total_sequence_length = sequence_length + pad_size

缩放 Query

    scale = 1 / (query.shape[-1] ** 0.5)
    query = query * scale

标准 attention 缩放法：1/sqrt(d_k)。

计算 V⋅β 与 K⋅β

    v_beta = value * beta.unsqueeze(-1)
    k_beta = key * beta.unsqueeze(-1)

把 β 当作权重，按 token 逐点缩放 Value / Key。β 控制 token 的"重要性"。

按 chunk 切分

    query, key, value, k_beta, v_beta = [
        x.reshape(x.shape[0], x.shape[1], -1, chunk_size, x.shape[-1]) for x in (query, key, value, k_beta, v_beta)
    ]

现在每个张量变成：形状是 (B, H, num_chunks, chunk_size, D)

对 g 分块

    g = g.reshape(g.shape[0], g.shape[1], -1, chunk_size)

构造 chunk 内上三角 mask

    mask = torch.triu(torch.ones(chunk_size, chunk_size, dtype=torch.bool, device=query.device), diagonal=0)

g 的累积和（表示 decay 累积）

    g = g.cumsum(dim=-1)

g 原本是 per-token 门控衰减值（负数）cumsum 之后用于构建指数衰减。

构造 chunk 内所有 token 两两之间的 decay mask

    decay_mask = ((g.unsqueeze(-1) - g.unsqueeze(-2)).tril().exp().float()).tril()

形状：(B, H, num_chunks, chunk_size, chunk_size)

含义：

• g[i] - g[j] 表示 token i → token j 的累计衰减
• 只取下三角（只能看过去）
• exp 后得到 decay（越远衰减越大）

计算 chunk 内自注意力矩阵

    attn = -((k_beta @ key.transpose(-1, -2)) * decay_mask).masked_fill(mask, 0)

步骤含义：

1. k_beta @ key^T：类似 attention score（但并不完全是 QK^T）
2. 乘 decay_mask，加入时间衰减
3. 取负号（说明这是某种 kernel-based 累积）
4. masked_fill 用 mask 清理未来 token（上三角）

对 chunk 内的 attention 做一个累积增强

    for i in range(1, chunk_size):
        row = attn[..., i, :i].clone()
        sub = attn[..., :i, :i].clone()
        attn[..., i, :i] = row + (row.unsqueeze(-1) * sub).sum(-2)

这段逻辑是 delta-rule 的核心：

• 逐行递归增强
• 类似 row += row * sub 的累积
• 这本质模拟 RNN-style recurrence in parallel

把对角线加 1 使矩阵可逆/稳定

    attn = attn + torch.eye(chunk_size, dtype=attn.dtype, device=attn.device)

应用注意力到 v_beta

    value = attn @ v_beta

得到 chunk 内加权的 value。

用衰减过的 key 构造一个"累积记忆项"

    k_cumdecay = attn @ (k_beta * g.exp().unsqueeze(-1))

这个项将在 chunk 之间递归更新。

初始递归状态

    last_recurrent_state = (
        torch.zeros(batch_size, num_heads, k_head_dim, v_head_dim).to(value)
        if initial_state is None
        else initial_state.to(value)
    )

last_recurrent_state 的形状是 (B, H, D_k, D_v)

表示跨 chunk 的记忆矩阵（类似 RNN 的 hidden state）。

core_attn_out 结果初始化

    core_attn_out = torch.zeros_like(value)

mask

    mask = torch.triu(torch.ones(chunk_size, chunk_size, dtype=torch.bool, device=query.device), diagonal=1)

跨 chunk 的递归（核心 RNN-like 更新）

    for i in range(0, total_sequence_length // chunk_size):

逐 chunk 处理。

取 chunk i 的 Q, K, V

        q_i, k_i, v_i = query[:, :, i], key[:, :, i], value[:, :, i]

计算 chunk 内 attention（包含 decay）

        attn = (q_i @ k_i.transpose(-1, -2) * decay_mask[:, :, i]).masked_fill_(mask, 0)

这是 QK^T * decay masking。

delta-rule 记忆预测值

        v_prime = (k_cumdecay[:, :, i]) @ last_recurrent_state

用递归状态预测当前 chunk 的 v。

v_new = 当前真实值 - 预测值（误差项）

        v_new = v_i - v_prime

delta-rule 的核心：用预测误差来更新状态。

q_i 通过门控衰减作用于记忆

        attn_inter = (q_i * g[:, :, i, :, None].exp()) @ last_recurrent_state

最终输出 chunk attention

        core_attn_out[:, :, i] = attn_inter + attn @ v_new

输出 =

• recurrence-based term（attn_inter）
• delta-based correction（attn @ v_new）

更新跨 chunk 的递归状态

        last_recurrent_state = (
            last_recurrent_state * g[:, :, i, -1, None, None].exp()
            + (k_i * (g[:, :, i, -1, None] - g[:, :, i]).exp()[..., None]).transpose(-1, -2) @ v_new
        )

分两部分：

1. last_state * decay ------ 旧记忆衰减
2. k_i * exp(delta g) @ v_new ------ 新信息按 delta-rule 替换/更新

如果不输出 final state，则置为 None

    if not output_final_state:
        last_recurrent_state = None

恢复到原来的 (B, L, H, D) 格式

    core_attn_out = core_attn_out.reshape(core_attn_out.shape[0], core_attn_out.shape[1], -1, core_attn_out.shape[-1])
    core_attn_out = core_attn_out[:, :, :sequence_length]
    core_attn_out = core_attn_out.transpose(1, 2).contiguous().to(initial_dtype)

最终返回

    return core_attn_out, last_recurrent_state

总结（核心概念）

功能	描述
chunking	将长序列拆成 chunk，每段内部并行计算
g（门控衰减）	控制 token 之间的信息流衰减
β（重要性权重）	对 K/V 进行缩放，类似 attention mask
delta rule	v_new = v_real - v_pred，用误差更新递归状态
递归状态（跨 chunk）	类似 RNN hidden state，存储长期依赖
并行 + 递归混合	chunk 内并行，chunk 间递归

这是一个非常高效但复杂的 RNN+Attention 混合结构。

3.4.4 两个 mask 矩阵

关于代码中的两个 mask 矩阵，需要明确：

它们不属于注意力机制范畴，而是线性代数求解的技巧性设计。要理解 DeltaAttention（Qwen3-Next）作为"线性注意力"的关键在于：

问题核心 ：既然线性注意力不需要显式因果 mask，为何torch_chunk_gated_delta_rule中会出现torch.triu()这样的"因果矩阵"？这看似矛盾。

本质 ：这段代码中的 mask 并非"注意力因果矩阵"，而是 chunk 扫描（block-scan）为实现并行结构必须引入的"计算图约束 mask"，与 softmax/transformer 中的因果 mask 概念完全不同。

mask 的真实用途 ：确保 (I - A) S = B 这个线性系统成为严格下三角结构，从而可通过 prefix-scan（并行）求解递推关系。具体而言：

• 强制矩阵 A 成为"严格下三角矩阵"
• 实现三个目标：
  1. 高效求逆
  2. 可分块并行计算
  3. 防止块内递推时信息泄漏到未来块

关键区分：这是"线性代数结构 mask"，而非 attention mask。

为何需要块下三角结构？

DeltaAttention 的递推方程：
S t = α t S t − 1 + v t k t ⊤ S_t = \alpha_t S_{t-1} + v_t k_t^\top St=αtSt−1+vtkt⊤
本质是时间递推（RNN），无法直接并行。

FLA（flash-linear-attention）的解决方案：

将递推转化为块内线性系统求解：(I - A)S = B

其中 A 设计为下三角矩阵：

[1 0 0 0]
[a 1 0 0]
[b c 1 0]
[d e f 1]

为实现严格下三角特性，需要：

mask = torch.triu(..., diagonal=0)
attn = attn.masked_fill(mask, 0)

核心目的 ：确保矩阵可逆性 & 可并行化，而非实现因果性。

三角形状的数学意义：

1. 下三角矩阵 A ⇒ (I - A) 可并行求逆
2. 其幂 A², A³ 在有限步内归零（A 具有幂零性/nilpotent）
3. 可表示为有限前缀和：
   ( I − A ) − 1 = I + A + A 2 + A 3 + ... (I-A)^{-1} = I + A + A^2 + A^3 + \dots (I−A)−1=I+A+A2+A3+...

这正是 FLA 采用 GPU 并行 block-scan 算法的数学基础。

关键结论 ：

此 mask 的实质功能：

功能	类型
约束矩阵 A 结构	线性代数结构性 mask
确保并行可计算性	block-scan mask
维持严格下三角特性	数学条件
实现 ΔAttention 高效并行	工程优化

最终定义 ：

此 mask 是"块内递推方程并行求解所需的下三角强制掩码"，属于线性代数求解技巧，与注意力机制无关。

3.4.5 chunk 的并行技术

ΔAttention（Delta Rule）本质上是一个"像 RNN 一样"的递推结构，天然不能并行，但 FLA（flash-linear-attention）的 chunk 技术，把原来必须逐步计算的递推变成了可以在一个"块内部"并行计算的形式。

1、chunk_gated_delta_rule 计算的是未归一化的分子 ( S t q t ) (S_t q_t) (Stqt)

它不计算 softmax、也不计算归一化项 ( Z t Z_t Zt)。

因为 chunk 算子只负责计算 Delta Attention 的"记忆状态 S t S_t St" 。
S t S_t St 是 softmax attention 中的"分子部分"，但是 softmax attention 的最终输出还需要分母（归一化）：

o t = S t q t Z t q t o_t = \frac{S_t q_t}{Z_t q_t} ot=ZtqtStqt

chunk 算子只是 operator，不负责完整注意力逻辑。
Z t Z_t Zt 是在 Qwen3-Next Attention 层里计算的，不是在算子内部。

chunk 内做的事： 只算 ( S t q t S_t q_t Stqt)、 不算 ( Z t Z_t Zt)、不算归一化（softmax-like 分母）。

2、chunk 内不在计算注意力，而是求解 ΔAttention 的线性系统表示 (I - A)⁻¹

它是在解递推，不是在算注意力，是为了 把 RNN-式递推 S t = f ( S t − 1 , x t ) S_t = f(S_{t-1}, x_t) St=f(St−1,xt) 改写成可并行处理的形式。

ΔAttention 原始递推形式：

S t = α t S t − 1 + β t k t ( v t − S t − 1 k t ) ⊤ S_t = \alpha_t S_{t-1} + \beta_t k_t(v_t - S_{t-1}k_t)^\top St=αtSt−1+βtkt(vt−St−1kt)⊤

这是 严格顺序依赖 的：

必须先算 S₁，再算 S₂，再算 S₃......

chunk 技术做的事：

把多个时间步组合成一个线性系统：

S c h u n k = ( I − A ) − 1 B S_{chunk} = (I - A)^{-1} B Schunk=(I−A)−1B

这样就能：

• chunk 内 并行地 得到多个 S t S_t St
• chunk 间保持顺序

关键理解：

chunk 内看见的 mask、下三角矩阵、A 矩阵，不是注意力权重，而是用于"数值求解递推"的中间结构。

它们只是为了让 ΔAttention 能够并行。

3、虽然 chunk 内可以并行，但 chunk 与 chunk 之间仍然严格按时间顺序递推

块内可以并行，不代表整个序列并行。

chunk 内： 把 64 个 token 一起求解、是数学意义上的 局部求解 。

chunk 间： 必须按顺序更新 S t S_t St、因为 S t + 1 S_{t+1} St+1 依赖 S t S_t St、 S t S_t St 是注意力状态本质（像 RNN hidden state）、完整因果结构仍然保持。

图示：

Chunk 0 → Chunk 1 → Chunk 2 → ...
   ↓         ↓          ↓
 S_64     S_128      S_192   ...（顺序递推）

3.4.6 chunk 的并行技术原理解析

1、通俗易懂解析：

"递推"不能并行，但"求解递推方程"可以并行

普通递推：

S1 = f(S0, x1)
S2 = f(S1, x2)
S3 = f(S2, x3)
...

只能一个接一个算，因此是串行。

但 FLA 不是像这样直接算，而是：

把整个"块"的递推结构 改写成一个线性代数问题：解一个下三角线性方程组。

例如 4 个 token 的递推：

S0 → S1 → S2 → S3 → S4

被改写成：

(I - A) * S = B

其中 A 是下三角矩阵 （未来依赖过去 → 因果结构），这样的线性系统 可以一次性并行求解（block-scan）。

2、专业解析：

DeltaAttention 的核心更新式：

S t = α t S t − 1 + β t k t ( v t − S t − 1 k t ) ⊤ S_t = \alpha_t S_{t-1} + \beta_t k_t (v_t - S_{t-1}k_t)^\top St=αtSt−1+βtkt(vt−St−1kt)⊤

这是一个 线性-外积形式 的更新。

展开可得到：整体结构是前缀和（prefix-sum）形式：Sₜ = ∑贡献(i→t)，（这种结构天然是结合律友好的）

也就是说：

( S 3 = S 2 + C 3 ) , ( S 2 = S 1 + C 2 ) , ( S 1 = S 0 + C 1 ) (S_3 = S_2 + C_3), \quad (S_2 = S_1 + C_2), \quad (S_1 = S_0 + C_1) (S3=S2+C3),(S2=S1+C2),(S1=S0+C1)

可以变成：

S 3 = S 0 + C 1 + C 2 + C 3 S_3 = S_0 + C_1 + C_2 + C_3 S3=S0+C1+C2+C3

前缀和满足结合律，因此可以并行。

chunk 内矩阵 A 是什么？

FLA 构造的 A 是：

A i j = { − β j   k j ⊤ k i ⋅ α i : j , j < i 0 , j ≥ i A_{ij} = \begin{cases} -\beta_j \, \boldsymbol{k}_j^\top \boldsymbol{k}i \cdot \alpha{i:j}, & j < i \\ 0, & j \ge i \end{cases} Aij={−βjkj⊤ki⋅αi:j,0,j<ij≥i

即 A 是严格下三角。

于是：

S = ( I − A ) − 1 B S = (I - A)^{-1} B S=(I−A)−1B

而下三角的线性系统 可以通过 parallel scan 求解：

(I - A)⁻¹ = I + A + A² + A³ + ...

因为 A 是下三角且满足 Aᵏ = 0 (当 k > chunk_size)，这是一个有限级数。

prefix-scan 正好可以并行地计算：

I + A + A² + ...

这与 GPU 完美契合。

3.4.7 总结：

• ΔAttention（Delta Rule）本质上是一个"像 RNN 一样"的递推结构，天然不能并行，但 FLA（flash-linear-attention）的 chunk 技术，把原来必须逐步计算的递推变成了可以在一个"块内部"并行计算的形式。

• chunk operator 不是注意力，是 DeltaAttention 的并行化求解器：它算出未归一化的记忆态 ( S t S_t St)，而完整注意力（含归一化）在 Qwen3-Next 的 Attention 层里完成。

• chunk 本质上不是直接并行递推，而是把递推结构转化成一个"可并行求解的数学形式"（递推本来不能并行，但 ΔAttention 的特殊结构让递推可以改写为"前缀和"，前缀和可以并行求解，因此 chunk 可以并行。）。 这样全局看仍是递推，本地块内变成可并行。

---

3.5 算子 - fused_recurrent_gated_delta_rule

torch_recurrent_gated_delta_rule

def torch_recurrent_gated_delta_rule(
    query, key, value, g, beta, initial_state, output_final_state, use_qk_l2norm_in_kernel=False
):
    initial_dtype = query.dtype
    if use_qk_l2norm_in_kernel:
        query = l2norm(query, dim=-1, eps=1e-6)
        key = l2norm(key, dim=-1, eps=1e-6)
    query, key, value, beta, g = [
        x.transpose(1, 2).contiguous().to(torch.float32) for x in (query, key, value, beta, g)
    ]

    batch_size, num_heads, sequence_length, k_head_dim = key.shape
    v_head_dim = value.shape[-1]
    scale = 1 / (query.shape[-1] ** 0.5)
    query = query * scale

    core_attn_out = torch.zeros(batch_size, num_heads, sequence_length, v_head_dim).to(value)
    last_recurrent_state = (
        torch.zeros(batch_size, num_heads, k_head_dim, v_head_dim).to(value)
        if initial_state is None
        else initial_state.to(value)
    )

    for i in range(sequence_length):
        q_t = query[:, :, i]
        k_t = key[:, :, i]
        v_t = value[:, :, i]
        g_t = g[:, :, i].exp().unsqueeze(-1).unsqueeze(-1)
        beta_t = beta[:, :, i].unsqueeze(-1)

        last_recurrent_state = last_recurrent_state * g_t
        kv_mem = (last_recurrent_state * k_t.unsqueeze(-1)).sum(dim=-2)
        delta = (v_t - kv_mem) * beta_t
        last_recurrent_state = last_recurrent_state + k_t.unsqueeze(-1) * delta.unsqueeze(-2)
        core_attn_out[:, :, i] = (last_recurrent_state * q_t.unsqueeze(-1)).sum(dim=-2)

    if not output_final_state:
        last_recurrent_state = None
    core_attn_out = core_attn_out.transpose(1, 2).contiguous().to(initial_dtype)
    return core_attn_out, last_recurrent_state

这个函数实现了 Qwen3-next 使用的一种 RNN 化的注意力机制 。它不使用传统 Transformer 的 Softmax Attention，而改用一种 动态记忆矩阵 M_t 来处理序列。

核心思想：随着序列前进，用 key/value 逐步更新一个 d_k × d_v 的记忆矩阵，再用 query 从中读取输出。

整个过程是在线更新记忆矩阵，不用保存所有过去的 K/V 值，所以推理非常高效。

---

（1）预处理输入

• 可选：对 query/key 做 L2 归一化
• 把维度转成 (B, H, L, D)
• 转成 float32 计算
• 对 query 做 scale 缩放（同传统 attention）

（2）初始化记忆矩阵 M

last_recurrent_state  # shape = (B, H, d_k, d_v)

• 这是 attention 的"动态 KV 记忆"
• 初始为全 0 或给定初始状态

（3）对序列逐 token 处理（核心循环）

对每一步 t，执行如下操作：

---

（a） 读出 q_t, k_t, v_t, 门控 g_t 和学习率 beta_t

（b） 用 g_t 对记忆做遗忘衰减

M_t ← g_t * M_{t-1}

g_t = exp(g) 确保门控 > 0。

（c） 计算当前记忆 M 对 v_t 的预测

kv_mem = M_t @ k_t

也就是根据 key 方向从记忆读出 predicted value。

（d） 根据误差更新记忆（Delta Rule）

delta = (v_t - kv_mem) * beta_t
M_t ← M_t + k_t ⊗ delta

含义：

• (v_t - kv_mem) 是"模型对 v 的预测误差"
• beta_t 是动态学习率
• 外积更新 k_t ⊗ delta 是 往记忆写入信息

这部分是整个算法的核心。

（e） 用 query 读出当前注意力输出

output_t = M_t @ q_t

等价于：query 是"读指针"，key 是"写指针"，value 是内容。

（4）返回整段序列的输出与最终记忆

---

总结

这段代码实现的不是传统 Attention，而是：

一个带遗忘门 (g)、带学习率 (β) 的动态记忆 RNN Attention：用 key/value 的误差信号不断更新记忆矩阵，再用 query 读取输出。

其结构比 Softmax Attention 轻得多，适合长序列和 KV cache 替代。

参考

• src/transformers/models/qwen3_next/modeling_qwen3_next.py
• Qwen3-Next模型剖析
• Gated Delta Networks: Improving Mamba2 with Delta Rule
• Gated Attention for Large Language Models: Non-linearity, Sparsity, and Attention-Sink-Free
• Auxiliary-Loss-Free Load Balancing Strategy for Mixture-of-Experts
• Qwen/Qwen3-Next-80B-A3B-Instruct