摘要
大型语言模型已被广泛采用,但推理过程需要大量 GPU 内存。我们针对 Transformer 中的前馈层和注意力投影层 ,提出了一种 8 位整数(Int8)矩阵乘法方案,该方案能将推理所需内存减少一半,同时保持全精度性能。借助我们的方法,一个 1750 亿参数的 16 位 / 32 位模型检查点可以被加载、转换为 8 位格式,并立即投入使用,且不会出现性能下降。
这一成果的实现,得益于我们对 Transformer 语言模型中高度系统性涌现特征的理解与适配 ------ 这些特征主导着注意力机制和模型的预测性能。为应对这些特征,我们设计了两阶段量化方案 LLM.int8 ():首先,采用向量级量化,为矩阵乘法中的每个内积分配独立的归一化常数,对大部分特征进行量化;
其次,针对涌现出的异常值特征,提出一种新的混合精度分解策略,将异常值特征维度分离出来进行 16 位矩阵乘法,而其余超过 99.9% 的数值仍采用 8 位乘法。实证结果表明,使用 LLM.int8 () 可以在高达 1750 亿参数的大型语言模型上进行推理,且无任何性能损失。这一结果极大地提升了此类模型的可访问性,例如,使得在配备消费级 GPU 的单台服务器上运行 OPT-175B/BLOOM 成为可能。我们已开源相关软件 3。
3 https://github.com/TimDettmers/bitsandbytes
1 引言
大规模预训练语言模型在自然语言处理领域得到了广泛应用(Vaswani 等人,2017;Radford 等人,2019;Brown 等人,2020;Zhang 等人,2022),但它们的推理过程需要占用大量内存。对于参数规模达到并超过 67 亿的大型 Transformer 语言模型,前馈层、注意力投影层及其矩阵乘法操作占据了 95% 的模型参数,且贡献了 65%-85% 的计算量(Ilharco 等人,2020)2。减少参数占用空间的一种方法是将参数量化为更低的比特数,并采用低比特精度矩阵乘法。为此,研究人员已开发出针对 Transformer 的 8 位量化方法(Chen 等人,2020;Lin 等人,2020;Zafrir 等人,2019;Shen 等人,2020)。
然而,这些方法虽能减少内存使用,却会导致性能下降,通常需要在训练后进一步调整量化参数,且仅在参数小于 3.5 亿的模型上进行过研究。目前,对于参数高达 3.5 亿的模型,无性能损失的量化技术仍缺乏深入理解,而数十亿参数模型的量化更是一项开放性挑战。其他参数主要来自嵌入层,仅有少量来自归一化层和偏置项。
本文首次提出一种适用于数十亿参数规模 Transformer 的 8 位整数量化方案,该方案不会造成任何性能损失。借助这一方案,我们可以加载 16 位或 32 位权重的 1750 亿参数 Transformer 模型,将其前馈层和注意力投影层转换为 8 位格式,然后直接用于推理,且性能不受影响。
这一成果的实现,解决了两个关键挑战:一是参数规模超过 10 亿时对更高量化精度的需求;二是明确表征稀疏但系统性的大振幅异常值特征 ------ 这类特征在模型参数达到 67 亿规模后,会出现在所有 Transformer 层中,破坏量化精度。如图 1 所示,一旦这些异常值特征出现,C4 数据集上的推理困惑度(第 3 节)和零样本准确率都会因精度损失而下降。
我们的研究表明,通过方案的第一部分 ------ 向量级量化,可以在参数规模高达 27 亿的模型上保持性能不变。向量级量化将矩阵乘法视为一系列独立的行向量与列向量内积运算,因此可为每个内积分配独立的量化归一化常数,以提高量化精度。在进行下一步运算前,通过列归一化常数与行归一化常数的外积进行反归一化,即可恢复矩阵乘法的输出结果。
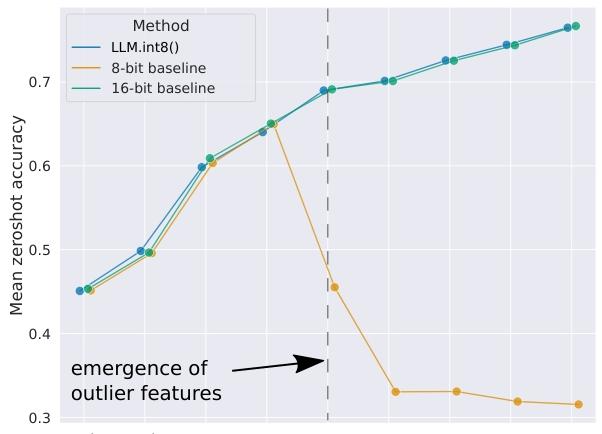
图 1:OPT 模型在 WinoGrande、HellaSwag、PIQA 和 LAMBADA 数据集上的平均零样本准确率。图中展示了 16 位精度基线、此前最精确的 8 位量化方法基线以及我们提出的新 8 位量化方法 LLM.int8 ()。可以看到,当参数规模达到 67 亿时,系统性异常值特征开始出现,传统量化方法失效,而 LLM.int8 () 仍能保持 16 位精度的性能。
要实现参数规模超过 67 亿的模型无性能损失量化,关键在于理解推理过程中隐藏状态特征维度中极端异常值的涌现规律。为此,我们进行了新的描述性分析,结果表明:振幅高达其他维度 20 倍的大特征,首先出现在约 25% 的 Transformer 层中 ,随着模型参数规模扩大到60 亿,这些特征会逐渐扩散到其他层;
当参数规模达到约 67 亿时,会发生相位转变 ,所有 Transformer 层和 75% 的序列维度都会受到大振幅特征的影响。这些异常值具有高度系统性 :在 67 亿参数规模下,每个序列会出现 15 万个异常值,但它们仅集中在整个 Transformer 的 6 个特征维度中。
尽管这些异常值特征仅占全部输入特征的约 0.1%,但将其置零后,注意力机制的 top-1 softmax 概率值会下降超过 20%,验证困惑度会恶化 600%-1000%;相比之下,随机移除相同数量的普通特征,概率值最大仅下降 0.3%,困惑度仅恶化约 0.1%。
为了在存在此类极端异常值的情况下实现有效量化,我们开发了方案的第二部分 ------ 混合精度分解。对于异常值特征维度,我们采用 16 位矩阵乘法;对于其余 99.9% 的维度,仍采用 8 位矩阵乘法。我们将向量级量化与混合精度分解相结合,命名为 LLM.int8 ()。实证结果表明,使用 LLM.int8 () 可以在高达 1750 亿参数的大型语言模型上进行推理,且无任何性能损失。该方法不仅揭示了异常值特征对模型性能的影响机制,还首次使得超大型模型(如 OPT-175B/BLOOM)能够在配备消费级 GPU 的单台服务器上运行。
尽管本文的核心目标是在不损失性能的前提下提高大型语言模型的可访问性,但附录 D 的实验结果表明,对于 BLOOM-176B 等大型模型,我们的方法能保持端到端推理 的运行时性能,且对于参数规模 67 亿 及以上的 GPT-3 模型, 可实现适度的矩阵乘法加速。我们已开源相关软件 3,并与 Hugging Face Transformers(Wolf 等人,2019)集成,使得所有支持线性层的 Hugging Face 托管模型都能使用该方法。
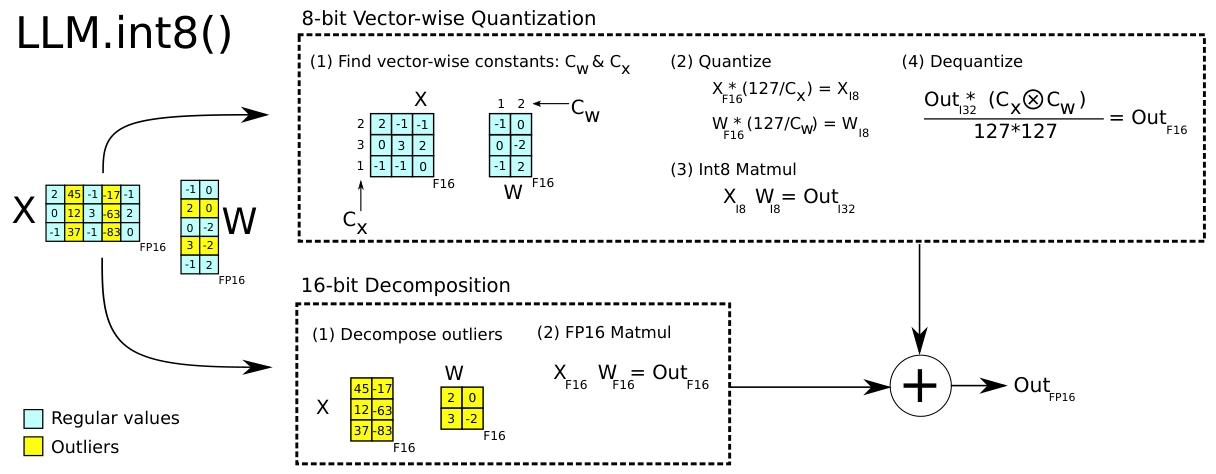
图 2:LLM.int8 () 的原理示意图。给定 16 位浮点输入Xf16和权重Wf16,首先将特征和权重分解为大振幅特征子矩阵和普通值子矩阵。异常值特征矩阵采用 16 位乘法运算,其余所有值采用 8 位乘法运算。8 位向量级乘法的实现过程为:通过行和列的绝对最大值Cx和Cw进行缩放,然后将输出量化为 8 位整数。对 32 位整数矩阵乘法的输出Outi32,通过归一化常数的外积Cx⊗Cw进行反量化。最后,将异常值特征的运算结果与普通特征的运算结果累加到 16 位浮点输出中。
2 背景
本研究将量化技术推向极限,探索其在 Transformer 模型规模扩大过程中的表现。我们重点关注两个问题:量化技术在何种规模下会失效、为何失效,以及这与量化精度之间的关系 ?为解答这些问题,我们研究了高精度非对称量化(零点量化)和对称量化(绝对最大值量化)。零点量化通过充分利用数据类型的全比特范围,可实现较高精度,但受实际条件限制,应用较少;绝对最大值量化则是目前最常用的量化技术。
2.1 8 位数据类型与量化方法
绝对最大值(Absmax)量化通过因子\( s_{x_{f16}} \)将输入缩放到8位整数范围[-127, 127],其中\( s_{x_{f16}} \)等于127除以整个张量的绝对最大值,相当于除以无穷范数后乘以127。因此,对于16位浮点输入矩阵\( X_{f16} \in \mathbb{R}^{s×h} \),8位整数绝对最大值量化可表示为:
\( X_{i8}=\left\lfloor \frac {127\cdot X_{f16}}{\operatorname* {max}{ij}\left( \left| X{f16_{ij}}\right| \right) }\right\rceil =\left\lfloor \frac {127}{\left\| X_{f16}\right\| {\infty }}X{f16}\right\rceil =\left\lfloor s_{x_{f16}}X_{f16}\right\rceil \)
其中,⌊⌉表示四舍五入到最近整数。
零点(Zeropoint)量化通过归一化动态范围\( nd_{x} \)进行缩放,再通过零点\( zp_x \)进行偏移,将输入分布映射到全范围[-127, 127]。通过这种仿射变换,任何输入张量都能充分利用数据类型的所有比特位,从而减少非对称分布的量化误差。例如,对于ReLU激活函数的输出,绝对最大值量化中[-127, 0)的比特位完全未被使用,而零点量化则能充分利用[-127, 127]的全部范围。零点量化的计算公式如下:
\( nd_{x_{f16}}=\frac{2 \cdot 127}{max {ij}\left(X{f16}^{ij}\right)-min {ij}\left(X{f16}^{ij}\right)} (1) \)
\( zp_{x_{i16}}=\left\lfloor X_{f16} \cdot min {ij}\left(X{f16}^{ij}\right)\right\rceil (2) \)
\( X_{i8}=\left\lfloor nd_{x_{f16}}X_{f16}\right\rfloor (3) \)
在运算中使用零点量化时,需将张量\( X_{i8} \)和零点\( zp_{x_{i16}} \)输入到特殊指令4中,该指令在执行16位整数运算前,会将\( zp_{x_{i16}} \)加到\( X_{i8} \)的每个元素上。例如,要计算两个零点量化数\( A_{i8} \)和\( B_{i8} \)(及其对应的零点\( zp_{a_{i16}} \)和\( zp_{b_{i16}} \))的乘积,公式如下:
\( C_{i32}={multiply}{i16}(A{zp_{a_{i16}}},B_{zp_{b_{i16}}})=(A_{i8}+zp_{a_{i16}})(B_{i8}+zp_{b_{i16}}) (4) \)
如果GPU或TPU等设备不支持multiplyi16指令,则需要展开计算:
\( C_{i32}=A_{i8}B_{i8}+A_{i8}zp_{b_{i16}}+B_{i8}zp_{a_{i16}}+zp_{a_{i16}}zp_{b_{i16}} (5) \)
其中,\( A_{i8}B_{i8} \)以8位整数精度计算,其余部分以16位或32位整数精度计算。在上述两种情况下,输出结果均以32位整数\( C_{i32} \)存储。要对\( C_{i32} \)进行反量化,需除以缩放常数\( nd_{a_{f16}} \)和\( nd_{b_{f16}} \)。
4 https://www.felixcloutier.com/x86/pmaddubsw
**输入和输出为16位浮点的8位整数矩阵乘法**:给定序列维度为s、特征维度为h、输出维度为o的隐藏状态\( X_{f16} \in \mathbb{R}^{s×h} \)和权重\( W_{f16} \in \mathbb{R}^{h×o} \),输入和输出为16位浮点的8位整数矩阵乘法运算如下:
\( \begin{array} {rl}{X_{f16}W_{f16}=C_{f16}}&{\approx \frac {1}{c_{x_{f16}}c_{w_{f16}}}C_{i32}=S_{f16}\cdot C_{i32}}\\ &{\approx S_{f16}\cdot A_{i8}B_{i8}=S_{f16}\cdot Q\left(A_{f16}\right) Q\left(B_{f16}\right) ,}\end{array} \)
其中,\( Q(\cdot) \)表示绝对最大值量化或零点量化,\( c_{x_{f16}} \)和\( c_{w_{f16}} \)分别为绝对最大值量化的张量级缩放常数\( s_x \)和\( s_w \),或零点量化的张量级缩放常数\( nd_x \)和\( nd_w \)。
3 大规模 8 位整数矩阵乘法
对于每个张量仅使用单个缩放常数的量化方法,一个关键挑战是:单个异常值会降低所有其他值的量化精度。因此,理想情况下应为每个张量分配多个缩放常数(如块级常数(Dettmers 等人,2022)),以将异常值的影响限制在单个块内。我们对一种常用的分块量化方法 ------ 行级量化(Khudia 等人,2021)进行了改进,提出了向量级量化,具体细节如下。
对于参数规模超过 67 亿的 Transformer 模型,所有层都会出现大振幅异常值特征,此时向量级量化已不再适用。为此,我们开发了混合精度分解技术:将占比约 0.1% 的大振幅特征维度以 16 位精度表示,其余 99.9% 的数值仍采用 8 位乘法。由于大部分数据仍以低精度表示,与 16 位精度相比,内存占用可减少约 50%。例如,对于 BLOOM-176B 模型,内存占用可减少 1.96 倍。
向量级量化和混合精度分解的原理如图 2 所示。LLM.int8 () 方法是绝对最大值向量级量化与混合精度分解的结合。
3.1 向量级量化
提高矩阵乘法缩放常数数量的一种方法是将矩阵乘法视为一系列独立的内积运算。给定隐藏状态\( X_{f16} \in \mathbb{R}^{b×h} \)和权重矩阵\( W_{f16} \in \mathbb{R}^{h×o} \),可为\( X_{f16} \)的每一行分配不同的缩放常数\( c_{x_{f16}} \),为\( W_{f16} \)的每一列分配不同的缩放常数\( c_w \)。反量化时,需通过\( 1/(c_{x_{f16}}c_{w_{f16}}) \)对每个内积结果进行反归一化。对于整个矩阵乘法,这相当于通过外积\( c_{x_{f16}} \otimes c_{w_{f16}} \)(其中\( c_x \in \mathbb{R}^s \),\( c_w \in \mathbb{R}^o \))进行反归一化。因此,带有行常数和列常数的矩阵乘法完整公式如下:
\( C_{f16} \approx \frac{1}{c_{x_{f16}} \otimes c_{w_{f16}}} C_{i32}=S \cdot C_{i32}=S \cdot A_{i8} B_{i8}=S \cdot Q\left(A_{f16}\right) Q\left(B_{f16}\right) (7) \)
我们将这种方法称为矩阵乘法的向量级量化。
3.2 LLM.int8 () 的核心:混合精度分解
我们的分析表明,数十亿参数规模8位Transformer量化面临的一个重要问题是:模型中存在对性能至关重要的大振幅特征(列向量),这类特征需要高精度量化。然而,作为我们最优的量化技术,向量级量化是对隐藏状态的每一行进行量化,无法有效处理异常值特征。幸运的是,这些异常值特征在实际应用中具有极高的稀疏性和系统性,仅占所有特征维度的约0.1%,这使得我们能够开发一种新的分解技术,专门针对这些维度进行高精度乘法运算。
研究发现,对于输入矩阵\( X_{f16} \in \mathbb{R}^{s×h} \),异常值特征在几乎所有序列维度s中都会系统性出现,但仅局限于特定的特征/隐藏维度h。因此,我们提出矩阵乘法的混合精度分解方法 :将异常值特征维度分离到集合\( O=\{i | i \in \mathbb{Z}, 0 ≤i ≤h\} \)中 ,该集合包含所有至少存在一个振幅大于阈值α的异常值的h维度。
本研究中,我们发现α=6.0足以将Transformer模型的性能损失降至接近零的水平。采用爱因斯坦求和符号(所有指标均为上标),给定权重矩阵\( W_{f16} \in \mathbb{R}^{h×o} \),矩阵乘法的混合精度分解定义如下:
\( C_{f16} \approx \sum {h \in O}X{f16}^{h} W_{f16}^{h}+S_{f16}\cdot \sum {h \notin O} X{i8}^{h} W_{i8}^{h} (8) \)
其中,\( S_{f16} \)是8位输入张量\( X_{i8} \)和权重矩阵\( W_{i8} \)的反归一化项。
这种8位与16位精度的分离设计,既实现了异常值特征的高精度乘法运算,又通过8位权重矩阵乘法保证了99.9%数值的内存高效性。对于参数规模高达130亿的Transformer模型,异常值特征维度数量不超过7(|O| ≤7),因此这种分解操作仅会增加约0.1%的内存占用。
3.3 实验设置
我们评估了不同量化方法在多种公开预训练语言模型上的鲁棒性,模型参数规模最高达 1750 亿。本研究的核心关注点并非单一模型上的量化性能,而是量化方法随模型规模扩大的性能变化趋势。
实验采用两种设置:一是基于语言建模困惑度(我们发现这是一种对量化损失高度敏感的鲁棒性指标),用于比较不同量化基线;二是评估 OPT 模型在一系列下游任务上的零样本准确率损失,并与 16 位精度基线进行对比。
在语言建模设置中,我们使用基于 fairseq(Ott 等人,2019)训练的稠密自回归 Transformer 模型,参数规模范围为 1.25 亿至 130 亿。这些 Transformer 模型在 Books(Zhu 等人,2015)、英文维基百科、CC-News(Nagel,2016)、OpenWebText(Gokaslan 和 Cohen,2019)、CC-Stories(Trinh 和 Le,2018)以及英文 CC100(Wenzek 等人,2020)数据集上进行预训练。关于这些预训练模型的训练细节,可参考 Artetxe 等人(2021)的研究。
为评估 8 位整数量化后的语言建模性能损失,我们在 C4 语料库(Raffel 等人,2019)的验证集上测试 8 位 Transformer 模型的困惑度,该语料库是 Common Crawl 语料库的一个子集 5。本实验使用 NVIDIA A40 GPU。
为衡量零样本性能损失,我们采用 OPT 模型(Zhang 等人,2022),并在 EleutherAI 语言模型评估框架(Gao 等人,2021)上进行评估。
3.4 主要结果
表 1 展示了参数规模从 1.25 亿到 130 亿的 8 位整数模型在 C4 语料库上的语言建模困惑度结果。可以看到,随着模型规模扩大,绝对最大值量化、行级量化和零点量化都会失效 ------ 参数超过 27 亿后,模型性能反而低于更小参数规模的模型;零点量化则在参数超过 67 亿后失效。我们提出的 LLM.int8 () 是唯一能保持困惑度不变的方法,因此也是唯一具有良好缩放趋势的量化方法。
表 1:不同规模(1.25 亿至 130 亿参数)Transformer 模型的量化方法在 C4 数据集上的验证困惑度。可以看到,随着模型规模扩大,绝对最大值量化、行级量化、零点量化和向量级量化都会导致显著的性能损失,尤其是在 130 亿参数规模下,8 位量化模型的困惑度甚至低于 67 亿参数规模的 8 位量化模型。使用 LLM.int8 () 可以在模型规模扩大时恢复全精度困惑度。由于零点量化是一种非对称量化方法,因此具有一定优势,但在结合混合精度分解后,这种优势会消失。
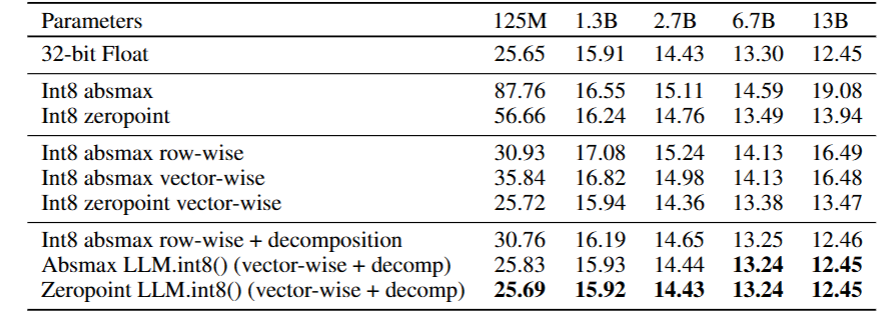
图 1 展示了 OPT 模型在 EleutherAI 语言模型评估框架上的零样本性能缩放趋势。可以看到,LLM.int8 () 在模型参数从 1.25 亿扩大到 1750 亿的过程中,始终保持 16 位精度的性能;而基线方法(绝对最大值向量级量化)的缩放性能较差,最终会退化为随机性能水平。
尽管本研究的核心重点是节省内存,但我们也对 LLM.int8 () 的运行时间进行了测量。与 16 位浮点基线相比,量化和分解的额外开销会导致参数小于 67 亿的模型推理速度变慢。然而,这类模型通常可以适配大多数 GPU,实际应用中对量化的需求较低。对于 1750 亿参数模型中的大型矩阵乘法,LLM.int8 () 的运行速度约为 16 位精度的两倍。附录 D 提供了这些实验的详细信息。
4 大规模 Transformer 中的大振幅涌现特征
随着 Transformer 模型规模扩大,会涌现出大振幅异常值特征,这些特征会对所有层及其量化过程产生强烈影响。给定隐藏状态X∈Rs×h(其中 s 为序列 / 令牌维度,h 为隐藏 / 特征维度),我们将某个特定维度hi定义为一个特征。本研究分析了特定特征维度hi在给定 Transformer 所有层中的表现。
研究发现,异常值特征对注意力机制和 Transformer 的整体预测性能具有显著影响。对于 130 亿参数模型,每个 2048 令牌序列中最多存在 15 万个异常值特征,但这些特征具有高度系统性,仅对应最多 7 个独特的特征维度hi。这一分析结论对混合精度分解技术的开发至关重要,同时也解释了零点量化的优势、混合精度分解为何会抵消这种优势,以及小型模型与大型模型在量化性能上的差异。
4.1 异常值特征的识别
对涌现现象进行定量分析面临两大挑战:一是需选择少量特征进行分析,以确保结果清晰易懂且不过于复杂;二是需捕捉重要的概率模式和结构模式。为此,我们采用实证方法确定识别约束条件,将异常值特征定义为满足以下标准的特征:振幅至少为 6.0、影响至少 25% 的层、影响至少 6% 的序列维度。
更正式地说,给定一个具有 L 层的 Transformer 模型,其隐藏状态为Xl∈Rs×h(l=0...L,其中 s 为序列维度,h 为特征维度),我们将任意隐藏状态xli中的特定维度hi定义为一个特征。我们追踪满足以下条件的维度hi(0 ≤i ≤h):该维度中至少存在一个振幅α≥6的值;且这些异常值在至少 25% 的 Transformer 层(0...L)中的同一特征维度hi出现,并在所有隐藏状态xl的至少 6% 的序列维度 s 中出现。由于特征异常值仅出现在注意力投影层(键 / 查询 / 值 / 输出)和前馈网络扩展层(第一个子层),因此本分析忽略注意力函数和前馈网络收缩层(第二个子层)。
设定上述阈值的原因如下:研究发现,使用混合精度分解时,若将振幅≥6 的特征视为异常值特征,可避免困惑度损失;对于异常值影响的层数量,大型模型中的异常值特征具有系统性 ------ 要么在大多数层中出现,要么完全不出现,而小型模型中的异常值特征则具有随机性 ------ 仅在部分序列的部分层中出现。
因此,我们设定的层影响阈值可确保在最小的 1.25 亿参数模型中仅检测到一个异常值特征,该阈值对应 "至少 25% 的 Transformer 层在同一特征维度中出现异常值"。第二常见的异常值仅在单个层(占总层数的 2%)中出现,这表明该阈值具有合理性。对于序列维度影响阈值,我们采用相同的方法确定:在 1.25 亿参数模型中,异常值至少影响 6% 的序列维度。
本研究测试的模型参数规模最高达 130 亿。为确保观察到的现象并非由软件漏洞导致,我们评估了基于三种不同软件框架训练的 Transformer 模型:4 个使用 OpenAI 软件的 GPT-2 模型、5 个使用 Fairseq(Ott 等人,2019)的 Meta AI 模型,以及 1 个使用 Tensorflow-Mesh(Shazeer 等人,2018)的 EleutherAI GPT-J 模型。附录 C 提供了更多细节。此外,我们还在两种不同的推理软件框架(Fairseq 和 Hugging Face Transformers(Wolf 等人,2019))中进行了分析。
4.2 异常值特征的影响测量
为验证异常值特征对注意力机制和预测性能的重要性,我们在将隐藏状态xl输入注意力投影层之前,将异常值特征置零,然后将 top-1 softmax 概率与保留异常值特征的常规 softmax 概率进行对比。为避免级联误差并隔离异常值特征的影响,我们对所有层独立进行该操作,即向前传播常规 softmax 概率值。同时,我们还报告了移除异常值特征维度(将其置零)并将修改后的隐藏状态传播通过整个 Transformer 后的困惑度损失。作为对照,我们对随机选择的非异常值特征维度执行相同操作,并记录注意力机制和困惑度的损失情况。
主要定量结果可总结为以下四点:
(1)以参数数量为衡量标准,大振幅特征在 Transformer 所有层中的涌现具有突发性 ------ 如图 3a 所示,当参数规模在 60 亿至 67 亿之间时,受影响的层比例从 65% 跃升至 100%,受影响的序列维度比例从 35% 迅速增至 75%。这一突变与量化方法开始失效的节点一致。
(2)以困惑度为衡量标准,大振幅特征在 Transformer 所有层中的涌现呈现平滑的指数增长趋势 ------ 随着困惑度降低,涌现特征逐渐增多(如图 3b 所示)。这表明特征涌现并非突然发生,通过研究小型模型的指数趋势,我们可能在相位转变发生前就检测到涌现特征。同时,这也意味着特征涌现不仅与模型规模相关,还与困惑度有关,而困惑度又受到训练数据量、数据质量等多种因素的影响(Hoffmann 等人,2022;Henighan 等人,2020)。
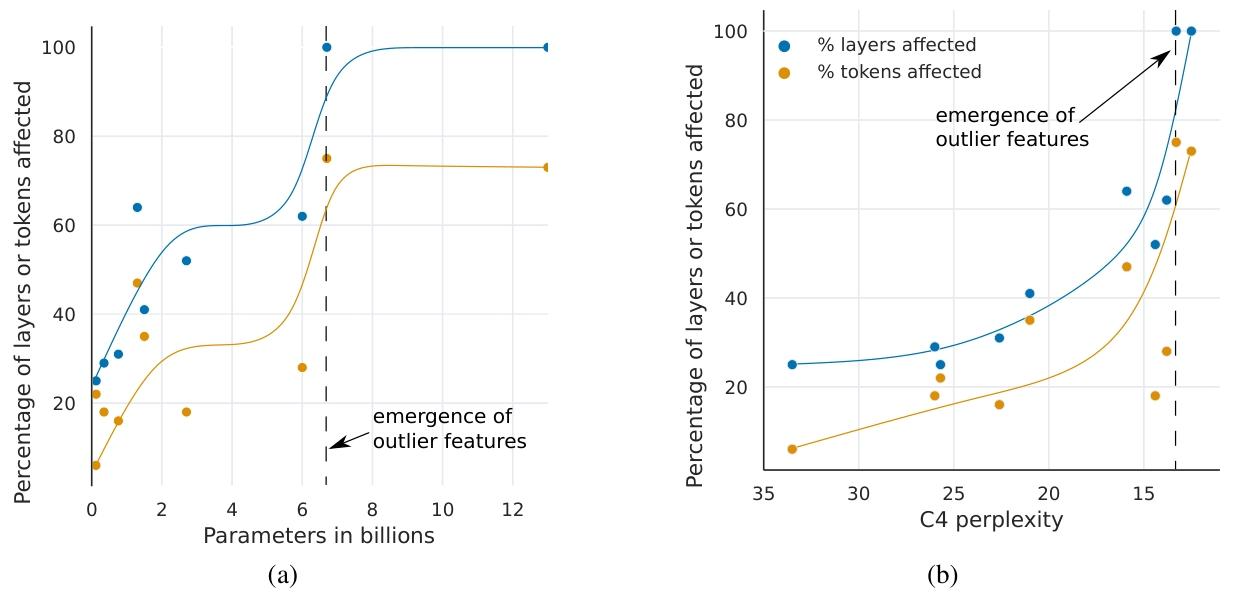
图 3:(a)按模型参数规模统计,(b)按 C4 数据集困惑度统计,Transformer 中受大振幅异常值特征影响的层比例和所有序列维度比例。图中线条为(a)4 段和(b)9 段线性分段的 B 样条插值。相位转变发生后,所有层都会出现异常值特征,约 75% 的序列维度会受到影响。(a)显示参数规模突变,(b)显示随着困惑度降低,相位转变呈渐进式指数增长。(a)中的显著突变与量化方法性能突然下降的节点一致。
(3)如图 4a 所示,一旦所有 Transformer 层中都出现异常值特征,异常值特征的中值振幅会迅速增大。异常值特征的大振幅及其非对称分布会破坏 8 位整数量化精度,这是量化方法在参数规模达到 67 亿后失效的核心原因 ------ 量化分布的范围过大,导致大多数量化区间为空,小量化值被量化为零,本质上造成了信息丢失。我们推测,除 8 位整数推理外,参数规模超过 67 亿后,常规 16 位浮点训练也会因异常值特征而变得不稳定 ------ 若与振幅为 60 的向量相乘,很可能会超出 16 位浮点的最大值 65535。
(4)如图 4b 所示,异常值特征的数量随 C4 数据集困惑度降低而严格单调增加,而与模型规模的关系则非单调。这表明,决定相位转变的是模型困惑度,而非单纯的模型规模。我们推测,模型规模只是实现特征涌现所需的众多重要协变量之一。
图 4:(a)最大异常值特征的中值振幅显示异常值规模存在突变,这似乎是量化方法在特征涌现后失效的主要原因。尽管异常值特征维度的数量与模型规模仅呈粗略的比例关系,但(b)显示,在所有分析的模型中,异常值特征的数量与困惑度呈严格单调关系。图中线条为 9 段线性分段的 B 样条插值。
相位转变发生后,这些异常值特征具有高度系统性。例如,对于序列长度为 2048 的 67 亿参数 Transformer 模型,整个模型的每个序列中约有 15 万个异常值特征,但这些特征仅集中在 6 个不同的隐藏维度中。
这些异常值特征对 Transformer 的性能至关重要:若移除异常值特征,平均 top-1 softmax 概率会从约 40% 降至约 20%,验证困惑度会增加 600%-1000%,尽管异常值特征维度最多仅为 7 个。相比之下,若随机移除 7 个特征维度,top-1 概率仅下降 0.02%-0.3%,困惑度仅增加 0.1%。这凸显了这些特征维度的关键作用 ------ 异常值特征的量化精度至关重要,即使是微小的误差也会对模型性能产生重大影响。
4.3 量化性能的解读
我们的分析表明,异常值特征在大型 Transformer 模型中普遍存在,且这些特征维度对模型性能至关重要。由于行级量化和向量级量化是对隐藏状态的每个序列维度 s(行)进行缩放,而异常值特征出现在特征维度 h(列)中,因此这两种方法都无法有效处理异常值特征 ------ 这也是绝对最大值量化方法在特征涌现后迅速失效的原因。
然而,几乎所有异常值特征都具有严格的非对称分布(仅为正值或仅为负值,见附录 C)。零点量化作为一种非对称量化方法,可将这些异常值特征缩放到全范围 [-127, 127],因此对异常值特征具有特别好的处理效果 ------ 这也解释了表 1 中量化缩放基准测试的结果。但在 130 亿参数规模下,由于量化误差累积和异常值振幅快速增大(如图 4a 所示),即使是零点量化也会失效。
若使用完整的 LLM.int8 () 方法(结合混合精度分解),零点量化的优势会消失,这表明分解后剩余的特征具有对称性。但向量级量化仍优于行级量化,这表明要保持全精度预测性能,需要提高模型权重的量化精度。
5 相关工作
以下将介绍与量化数据类型和 Transformer 量化相关的密切相关工作。附录 B 提供了卷积网络量化的更多相关工作。
8 位数据类型:本研究聚焦于 8 位整数(Int8)数据类型的量化技术,因为它是目前 GPU 唯一支持的 8 位数据类型。其他常见的 8 位数据类型包括定点或浮点 8 位数据类型(FP8),这类数据类型通常包含一个符号位,以及不同的指数位和尾数位组合。例如,一种常见的 FP8 数据类型包含 5 个指数位和 2 个尾数位(Wang 等人,2018;Sun 等人,2019;Cambier 等人,2020;Mellempudi 等人,2019),无需缩放常数或采用零点缩放。由于仅含 2 个尾数位,这类数据类型对大振幅值的误差较大,但对小振幅值的精度较高。Jin 等人(2022)的研究深入分析了针对特定标准差的输入,何种定点指数位 / 尾数位宽度最为最优。我们认为,FP8 数据类型的性能优于 Int8 数据类型,但目前 GPU 和 TPU 均不支持该数据类型。
语言模型中的异常值特征:语言模型中的大振幅异常值特征已被研究过(Timkey 和 van Schijndel,2021;Bondarenko 等人,2021;Wei 等人,2022;Luo 等人,2021)。已有研究证明了 Transformer 中异常值特征的出现与层归一化、令牌频率分布之间的理论关系(Gao 等人,2019)。类似地,Kovaleva 等人(2021)将 BERT 模型家族中异常值特征的出现归因于层归一化(LayerNorm),而 Puccetti 等人(2022)通过实证研究表明,异常值特征的涌现与训练分布中的令牌频率相关。本研究进一步扩展了这些工作,揭示了自回归模型规模与异常值特征涌现特性之间的关系,并证明了对异常值特征进行适当建模对于实现有效量化的关键作用。
数十亿参数规模 Transformer 量化:有两项与本研究并行开展的工作:nuQmm(Park 等人,2022)和 ZeroQuant(Yao 等人,2022)。这两种方法均采用分组量化方案,其量化归一化常数的粒度比向量级量化更细。该方案可提供更高的量化精度,但需要自定义 CUDA 内核。nuQmm 和 ZeroQuant 的目标是加速推理并减少内存占用,而本研究的重点是在 8 位内存占用下保持预测性能。nuQmm 和 ZeroQuant 评估的最大模型分别为 27 亿参数和 200 亿参数 Transformer,其中 ZeroQuant 实现了 200 亿参数模型 8 位量化的零性能损失。本研究则证明,我们的方法可实现高达 1760 亿参数模型的零性能损失量化。nuQmm 和 ZeroQuant 的研究表明,更细粒度的量化是大型模型量化的有效手段,这些方法与 LLM.int8 () 具有互补性。另一项并行工作是 GLM-130B,该模型借鉴了本研究的思路,实现了零性能损失的 8 位量化(Zeng 等人,2022)。GLM-130B 采用 8 位权重存储,结合全 16 位精度矩阵乘法。
6 讨论与局限性
本文首次证明,数十亿参数规模的 Transformer 模型可以被量化为 8 位整数格式,并立即用于推理,且不会造成任何性能损失。这一成果的实现,得益于我们对大规模模型中大振幅涌现特征的分析,并据此开发了混合精度分解技术,将异常值特征分离出来进行独立的 16 位矩阵乘法。结合向量级量化,我们提出了 LLM.int8 () 方法,实证结果表明,该方法可恢复高达 1750 亿参数模型的全精度推理性能。
本研究的主要局限性在于:分析仅针对 Int8 数据类型,未涉及 8 位浮点(FP8)数据类型。由于目前 GPU 和 TPU 均不支持 FP8 数据类型,因此我们认为这一主题更适合作为未来的研究方向,但同时也相信,从 Int8 数据类型中获得的许多见解可直接应用于 FP8 数据类型。第二个局限性是,我们仅在参数规模高达 1750 亿的模型上进行了研究 ------ 尽管我们实现了 1750 亿参数模型的 8 位量化且无性能损失,但在更大规模的模型上,可能会出现新的涌现特性,从而破坏我们的量化方法。
第三个局限性是,我们未将 8 位乘法应用于注意力函数。由于本研究的重点是减少内存占用,而注意力函数不包含任何参数,因此这并非必需。但初步探索表明,要解决这一问题,需要开发超出本研究范围的额外量化技术,因此我们将其留作未来的研究方向。
最后一个局限性是,本研究聚焦于推理过程,未涉及训练或微调。附录 E 提供了大规模 8 位整数微调与训练的初步分析。大规模 8 位整数训练需要在量化精度、训练速度和工程复杂度之间进行复杂权衡,是一项极具挑战性的任务,因此我们同样将其留作未来的研究方向。
7 更广泛影响
本研究的主要影响是提高了大型模型的可访问性 ------ 此前这些模型因 GPU 内存限制无法运行,而现在,资源有限的研究人员也能开展相关研究和应用(见表 3 中无需性能损失即可运行的模型 / GPU 组合)。然而,本研究也可能加剧资源差距:拥有大量 GPU 的资源丰富型组织可在相同数量的 GPU 上部署更多模型,从而扩大与资源匮乏型组织的差距。
表 2:不同硬件配置下,16 位精度与 8 位精度方法可运行的最大模型。可以看到,我们的 8 位精度方法使许多此前无法访问的模型变得可用,尤其是 OPT-175B/BLOOM。
我们认为,大型预训练模型的公开发布(例如最近的 Open Pretrained Transformers(OPT)(Zhang 等人,2022)),结合我们提出的用于零样本和少样本提示的 8 位整数推理技术,将为学术机构开辟新的研究方向 ------ 此前这些研究因资源限制无法开展。此类大规模模型的广泛可访问性可能会对社会产生有益和有害的双重影响,具体后果难以预测。
附录 A 与 16 位精度的内存占用对比
表 3 对比了不同开源模型在 16 位精度推理与 LLM.int8 () 方法下的内存占用。可以看到,LLM.int8 () 允许在配备消费级 GPU 的单节点上运行最大的开源模型 OPT-175B 和 BLOOM-176B。
表 3:不同硬件配置下,16 位精度与 8 位精度方法可运行的最大模型。可以看到,我们的 8 位精度方法使许多此前无法访问的模型变得可用,尤其是 OPT-175B/BLOOM。
附录 B 补充相关工作
参数小于 10 亿的 Transformer 量化:Transformer 量化研究此前主要集中在参数小于 10 亿的掩码语言模型(MLM),包括 BERT(Devlin 等人,2018)和 RoBERTa(Liu 等人,2019)。8 位精度的 BERT/RoBERTa 变体包括 Q8BERT(Zafrir 等人,2019)、QBERT(Shen 等人,2020)、带量化噪声的乘积量化(Fan 等人,2020)、TernaryBERT(Zhang 等人,2020)和 BinaryBERT(Bai 等人,2021)。Zhao 等人(2021)的研究同时涉及量化和剪枝。所有这些模型都需要量化感知微调或训练后量化,才能在低精度下使用。相比之下,我们的方法无需这些步骤,可直接使用,且无性能损失。
若将矩阵乘法视为 1×1 卷积,则向量级量化相当于卷积的通道级量化与行量化相结合(Khudia 等人,2021)。Wu 等人(2020)将这种方法用于 BERT 规模的 Transformer 模型(3.5 亿参数),而本研究首次将向量级量化应用于自回归模型和大规模模型。据我们所知,另一项针对非 BERT 类 Transformer 的量化研究是 Chen 等人(2020),该研究在正向传播中采用零点量化,在反向传播中采用行级零点量化,但仍局限于参数小于 10 亿的 Transformer 模型。我们的评估对比了零点量化和行级量化,且无需训练后量化。
低比特宽度与卷积网络量化:比特宽度小于 8 位的数据类型量化研究通常针对卷积网络(CNN),目的是减少内存占用、提高移动设备的推理速度,同时最大限度地减少模型性能损失。研究人员已对不同比特宽度的方法进行了探索:1 位方法(Courbariaux 和 Bengio,2016;Rastegari 等人,2016;Courbariaux 等人,2015)、2-3 位方法(Zhu 等人,2017;Choi 等人,2019)、4 位方法(Li 等人,2019)、更高比特宽度方法(Courbariaux 等人,2014)或可变比特宽度方法(Gong 等人,2019)。更多相关工作可参考 Qin 等人(2020)的综述。我们认为,数十亿参数规模的 Transformer 模型可采用比特宽度小于 8 位的量化方法,但会造成一定性能损失;而本研究聚焦于无性能损失的 8 位精度 Transformer 量化,这类模型可借助支持 8 位整数张量核心的常用 GPU 加速推理。
卷积网络量化的另一研究方向是通过学习调整量化过程来减少量化误差。例如,利用海森矩阵信息(Dong 等人,2019)、步长量化(Esser 等人,2019)、软量化(Gong 等人,2019)、基于线性规划优化的混合精度量化(Yao 等人,2021)以及其他学习型量化方法(Zhang 等人,2018;Gholami 等人,2021)。
附录 C 异常值特征详细数据
表 4 提供了异常值特征分析的制表数据,包括每个 Transformer 模型中最常见异常值的四分位数,以及单侧异常值(即分布不跨零的非对称分布异常值)的数量。
表 4:振幅≥6、影响至少 25% 的层和至少 6% 的序列维度的异常值特征统计摘要。可以看到,C4 验证集困惑度越低,异常值特征数量越多。异常值特征通常为单侧分布,其四分位数的最大范围表明,异常值特征的振幅是其他特征维度最大振幅的 3-20 倍 ------ 其他特征维度的振幅范围通常为 [-3.5, 3.5]。随着模型规模扩大,异常值特征在 Transformer 所有层中的出现频率越来越高,且几乎覆盖所有序列维度。当参数规模达到 67 亿时,会发生相位转变 ------ 同一异常值特征在所有层的同一特征维度中出现,且覆盖约 75% 的序列维度(SDim)。尽管异常值特征仅占所有特征的约 0.1%,但对获得较大的 softmax 概率至关重要 ------ 若移除异常值特征,平均 top-1 softmax 概率会下降约 20%。由于异常值特征在序列维度 s 上大多呈非对称分布,因此这些异常值维度会破坏对称的绝对最大值量化,更适合非对称的零点量化 ------ 这也解释了我们的验证困惑度分析结果。这些观察结果具有普遍性:在不同软件框架(fairseq、OpenAI、Tensorflow-mesh)训练的模型中均存在,在不同推理框架(fairseq、Hugging Face Transformers)中也均存在;且对 Transformer 架构的微小变化(旋转嵌入、嵌入归一化、残差缩放、不同初始化方式)具有鲁棒性。
附录 D 推理速度提升与下降
D.1 矩阵乘法基准测试
尽管本研究的重点是提高内存效率以增强模型可访问性,但 8 位整数方法也常用于加速推理。我们发现,量化和分解的额外开销相当显著,仅当整个 GPU 被充分饱和时,8 位整数矩阵乘法才能体现优势 ------ 这仅在大型矩阵乘法中成立,即仅适用于模型维度≥4096 的大型语言模型。
表 5 展示了原始矩阵乘法和量化额外开销的详细基准测试结果。可以看到,在模型维度为 5140(隐藏层维度为 20560)时,cuBLASLt 中的原始 8 位整数矩阵乘法开始比 cuBLAS 快两倍。若输入需要量化、输出需要反量化(若并非整个 Transformer 都采用 8 位整数格式,则这是必需步骤),则在模型维度为 5140 时,与 16 位精度相比,速度提升会降至 1.6 倍。模型维度≤2560 的模型推理速度会变慢。添加混合精度分解会进一步降低推理速度,因此仅 130 亿参数和 1750 亿参数模型能实现速度提升。
通过为混合精度分解优化 CUDA 内核,这些数值有望显著改善。然而,我们也发现,与使用默认 PyTorch 和 NVIDIA 提供的量化内核(除 1750 亿参数模型外,所有矩阵乘法的速度都会变慢)相比,现有的自定义 CUDA 内核要快得多。
表 5:不同规模 GPT-3 模型前馈网络第一层隐藏层的矩阵乘法推理速度与 16 位精度的对比。隐藏层维度是模型维度的 4 倍。"无额外开销的 8 位精度" 速度提升假设无需进行量化或反量化。小于 1.0x 的值表示速度下降。仅当模型维度和隐藏层维度较大时,8 位整数矩阵乘法才能加速推理。
D.2 端到端基准测试
除矩阵乘法基准测试外,我们还在 Hugging Face 框架中测试了 BLOOM-176B 模型的端到端推理速度。Hugging Face 采用带缓存注意力值的优化实现。由于这类推理是分布式的,且依赖通信,因此我们预计 8 位整数推理的整体速度提升和下降幅度会较小 ------ 因为整体推理运行时间中,固定的通信开销占比较大。
我们将 8 位整数推理与 16 位精度进行基准测试对比,并尝试在 8 位整数推理中使用更大的批次大小或更少的 GPU(因为 8 位整数模型可在更少的设备上适配)。表 6 展示了基准测试结果。总体而言,8 位整数推理的速度略慢于 16 位精度,但每个令牌的延迟非常接近。
表 6:BLOOM-176B 模型不同推理类型的 GPU 数量消融研究。我们对比了量化后的 BLOOM-176B 模型与原生 BLOOM-176B 模型使用的 GPU 数量,并报告了不同批次大小下每个令牌的生成速度(毫秒)。我们的方法与 Hugging Face 的 transformers(Wolf 等人,2019)集成,并借助 Hugging Face 的 accelerate 库处理多 GPU 推理。通过使用比原生模型更少的 GPU,我们的方法可实现与原生模型相近的性能。
附录 E 训练结果
我们在多种训练设置下测试了 8 位整数训练,并与 32 位精度基线进行对比。测试设置包括:Transformer 的前馈网络采用 8 位整数格式(注意力层的线性投影是否采用 8 位整数格式分为两种情况)、注意力机制本身采用 8 位整数格式,所有设置均与 32 位精度性能进行对比。我们在两项任务上进行了测试:(1)语言建模 ------ 使用 RoBERTa 语料库的部分数据,包括 Books(Zhu 等人,2015)、CC-News(Nagel,2016)、OpenWebText(Gokaslan 和 Cohen,2019)和 CC-Stories(Trinh 和 Le,2018);(2)神经机器翻译(NMT)(Ott 等人,2018)------ 使用 WMT14+WMT16 数据集(Macháček 和 Bojar,2014;Sennrich 等人,2016)。
表 7 和表 8 展示了测试结果。可以看到,在训练过程中,注意力线性投影采用 8 位整数数据类型和向量级量化会导致神经机器翻译(NMT)和 11 亿参数语言模型的性能下降,但对 2.09 亿参数语言模型无影响。使用混合精度分解后,结果略有改善,但在大多数情况下仍无法恢复全精度性能。这表明,前馈网络(FFN)层的 8 位整数训练相对简单,而其他层则需要额外的技术或不同于 8 位整数的数据类型,才能实现大规模无性能损失的 8 位训练。
表 7:小型和大型语言建模的初步结果。注意力机制采用 8 位整数格式会导致严重的性能下降,即使使用混合精度分解也无法完全恢复性能。对于小型语言模型,前馈网络(FFN)和注意力层的线性投影均采用 8 位整数格式时,性能接近基线;但在大型模型中,性能会下降。
表 8:WMT14+16 数据集上,前馈网络(FFN)和注意力线性层采用 8 位整数格式的神经机器翻译结果。"Decomp" 表示采用 16 位精度矩阵乘法的比例。BLEU 分数为 3 个随机种子的中值。
附录 F 微调结果
我们还在 RoBERTa-large 模型上测试了 8 位整数微调,微调任务为 GLUE。我们采用两种不同的设置:(1)与其他 8 位整数方法进行对比;(2)对比前馈网络(FFN)层和 / 或注意力投影层采用 8 位整数格式与 32 位精度的微调性能损失。微调过程使用 5 个随机种子,结果报告中值。
表 9 对比了不同现有 8 位整数微调方法,结果表明向量级量化优于其他方法。表 10 展示了前馈网络(FFN)和 / 或注意力线性投影采用 8 位整数格式的性能,以及使用混合精度分解后的性能改善。我们发现,前馈网络(FFN)层采用 8 位整数格式不会导致性能损失;而注意力线性投影采用 8 位整数格式时,若不结合混合精度分解(至少将振幅最大的 2% 维度采用 16 位精度计算),则会导致性能下降。这些结果表明,若要实现无性能损失的微调,当注意力线性投影也转换为 8 位整数格式时,混合精度分解至关重要。
表 9:前馈层采用 8 位整数格式、其余部分采用 16 位精度的 GLUE 微调结果(未使用混合精度分解)。可以看到,向量级量化优于基线方法。
表 10:前馈网络(FFN)和注意力线性层采用 8 位整数格式的 GLUE 微调性能分解(分数为 5 个随机种子的中值)。"Decomp" 表示分解为 16 位精度矩阵乘法的比例。与推理相比,若注意力线性层也转换为 8 位整数格式,微调需要更高的分解比例。