目录
-
- 摘要
- [1 引言](#1 引言)
-
- [1.1 量化技术的现状与挑战](#1.1 量化技术的现状与挑战)
- [1.2 OmniQuant的核心设计](#1.2 OmniQuant的核心设计)
- [1.3 OmniQuant的资源效率与性能优势](#1.3 OmniQuant的资源效率与性能优势)
- [1.4 本文贡献](#1.4 本文贡献)
- [2 相关工作](#2 相关工作)
-
- [2.1 量化方法分类](#2.1 量化方法分类)
- [2.2 大型语言模型的量化方向](#2.2 大型语言模型的量化方向)
-
- [2.2.1 仅权重量化](#2.2.1 仅权重量化)
- [2.2.2 权重-激活值联合量化](#2.2.2 权重-激活值联合量化)
- [3 OmniQuant方法](#3 OmniQuant方法)
-
- [3.1 LLM量化的核心挑战](#3.1 LLM量化的核心挑战)
- [3.2 块级量化误差最小化框架](#3.2 块级量化误差最小化框架)
-
- [3.2.1 优化目标](#3.2.1 优化目标)
- [3.2.2 框架优势](#3.2.2 框架优势)
- [3.3 可学习权重裁剪(LWC)](#3.3 可学习权重裁剪(LWC))
-
- [3.3.1 核心公式](#3.3.1 核心公式)
- [3.3.2 关键特性](#3.3.2 关键特性)
- [3.4 可学习等价变换(LET)](#3.4 可学习等价变换(LET))
-
- [3.4.1 核心思路](#3.4.1 核心思路)
- [3.4.2 线性层的等价变换](#3.4.2 线性层的等价变换)
- [3.4.3 注意力操作的等价变换](#3.4.3 注意力操作的等价变换)
- [4 实验](#4 实验)
-
- [4.1 实验设置](#4.1 实验设置)
-
- [4.1.1 量化配置](#4.1.1 量化配置)
- [4.1.2 训练参数](#4.1.2 训练参数)
- [4.1.3 模型与评估](#4.1.3 模型与评估)
- [4.2 仅权重量化结果](#4.2 仅权重量化结果)
-
- [4.2.1 泛化性强](#4.2.1 泛化性强)
- [4.2.2 低比特场景优势显著](#4.2.2 低比特场景优势显著)
- [4.2.3 适配多种量化方式](#4.2.3 适配多种量化方式)
- [4.3 权重-激活值联合量化结果](#4.3 权重-激活值联合量化结果)
-
- [4.3.1 显著提升低比特性能](#4.3.1 显著提升低比特性能)
- [4.3.2 超越QAT方法](#4.3.2 超越QAT方法)
- [4.3.3 W6A6配置下保持高精度](#4.3.3 W6A6配置下保持高精度)
- [4.4 指令微调模型的量化结果](#4.4 指令微调模型的量化结果)
-
- [4.4.1 LLaMA-2-7B-chat](#4.4.1 LLaMA-2-7B-chat)
- [4.4.2 LLaMA-2-13B-chat](#4.4.2 LLaMA-2-13B-chat)
- [4.5 实际设备上的推理加速](#4.5 实际设备上的推理加速)
-
- [4.5.1 显著降低内存占用](#4.5.1 显著降低内存占用)
- [4.5.2 大幅提升推理速度](#4.5.2 大幅提升推理速度)
- [4.5.3 硬件兼容性](#4.5.3 硬件兼容性)
- [5 结论](#5 结论)
- 致谢
- 附录(节选)
-
- [A1 OmniQuant算法伪代码](#A1 OmniQuant算法伪代码)
- [A2 与现有等价变换方法的区别](#A2 与现有等价变换方法的区别)
- [A3 消融实验(节选)](#A3 消融实验(节选))
-
- [A3.1 LWC与LET的协同作用](#A3.1 LWC与LET的协同作用)
- [A3.2 训练数据效率](#A3.2 训练数据效率)
- [A4 LLaMA系列模型的训练时间](#A4 LLaMA系列模型的训练时间)
- [A8 完整实验结果(节选)](#A8 完整实验结果(节选))
-
- [A8.1 Falcon-180B的仅权重量化结果](#A8.1 Falcon-180B的仅权重量化结果)
- 参考文献(节选)
摘要
大型语言模型(LLMs)彻底改变了自然语言处理任务,但巨大的内存与计算需求阻碍了其实际部署。尽管近年来的训练后量化(PTQ)方法在降低LLM内存占用、提升计算效率方面效果显著,但这些方法依赖人工设计量化参数,导致性能不佳,在极低比特量化场景下问题尤为突出。为解决这一问题,本文提出一种面向大型语言模型的全向校准量化技术(OmniQuant)。该技术通过高效优化各类量化参数,在多种量化设置下均能实现优异性能,同时保持训练后量化的计算效率。
OmniQuant包含两个创新组件:可学习权重裁剪(LWC)与可学习等价变换(LET)。其中,可学习权重裁剪通过优化裁剪阈值来调整权重极值;可学习等价变换则通过将量化难题从激活值转移到权重上,解决激活值异常值问题。OmniQuant基于块级误差最小化的可微框架运行,能够高效优化仅权重量化与权重-激活值联合量化过程。
例如,仅需128个样本,在单块A100-40G GPU上即可完成对LLaMA-2系列(70亿-700亿参数)模型的量化,耗时不超过116小时。大量实验验证了OmniQuant在多种量化配置(如W4A4(4比特权重、4比特激活值)、W6A6、W4A16、W3A16、W2A16)下的卓越性能。此外,OmniQuant在指令微调模型中同样有效,且在实际设备上能显著提升推理速度、减少内存占用。
代码开源地址:https://github.com/OpenGVLab/OmniQuant
1 引言
大型语言模型(如GPT-4(Bubeck等人,2023)、LLaMA(Touvron等人,2023a))在各类自然语言基准测试(Hendrycks等人,2020;Zellers等人,2019)中展现出惊人性能。此外,LLM固有的语言理解能力可成功迁移至多模态模型(Mu等人,2023;徐等人,2023;张等人,2023a;黄等人,2024;2023),因此LLM可被视为通用人工智能的重要前驱(Bubeck等人,2023)。
然而,LLM庞大的计算与内存需求带来了巨大挑战(张等人,2023b;胡等人,2023)。例如,GPT-3模型(Brown等人,2020)以FP16格式加载参数时需350G内存,这意味着推理至少需要5块A100-80G GPU。对计算资源的高额需求及随之而来的通信开销,阻碍了LLM在实际应用中的部署。
1.1 量化技术的现状与挑战
量化技术被证明是缓解LLM计算与内存开销的有效手段,主要分为两类:量化感知训练(QAT)与训练后量化(PTQ)。两种方法的对比与局限如下:
- 量化感知训练(QAT):通过在训练过程中模拟量化效果,能实现更具竞争力的精度,但需对整个模型进行重新训练,训练成本极高,不适用于超大规模LLM。
- 训练后量化(PTQ) :无需重新训练模型,效率更高,是现有LLM量化的主流选择。例如:
- 部分PTQ方法(Frantar等人,2022;Lin等人,2023;Dettmers等人,2023b)通过仅权重量化(量化权重、保持激活值全精度)降低内存消耗;
- 另一类PTQ方法(Xiao等人,2023;魏等人,2022;袁等人,2023)通过权重-激活值联合量化(将两者均量化为低比特)进一步减少计算开销,支持低比特矩阵乘法。
现有PTQ方法虽在W4A16(4比特权重、16比特激活值)、W8A8(8比特权重、8比特激活值)等配置下取得成果,但在W2A16、W4A4等极低比特场景下性能骤降(如图1(b)(c)所示)。核心原因在于这些方法依赖人工设计的量化参数(如迁移强度、缩放因子),无法适配复杂模型特性。
尽管QAT(如LLM-QAT(Liu等人,2023b))能优化量化参数,但资源消耗极高:例如,GPTQ(PTQ方法)量化LLaMA-13B仅需1小时、128个样本,而LLM-QAT需10万个样本、数百GPU小时。这引发核心问题:能否在保持PTQ时间与数据效率的同时,实现QAT级别的性能?
1.2 OmniQuant的核心设计
本文提出的OmniQuant技术有效解决了上述问题,其核心特性如下:
- 精度与效率兼顾:在多种量化场景(尤其是极低比特)下实现当前最优性能,同时保持PTQ的资源效率(如图1所示)。
- 轻量优化策略:冻结原始全精度权重,仅引入少量可学习量化参数,避免QAT的全局权重优化成本。
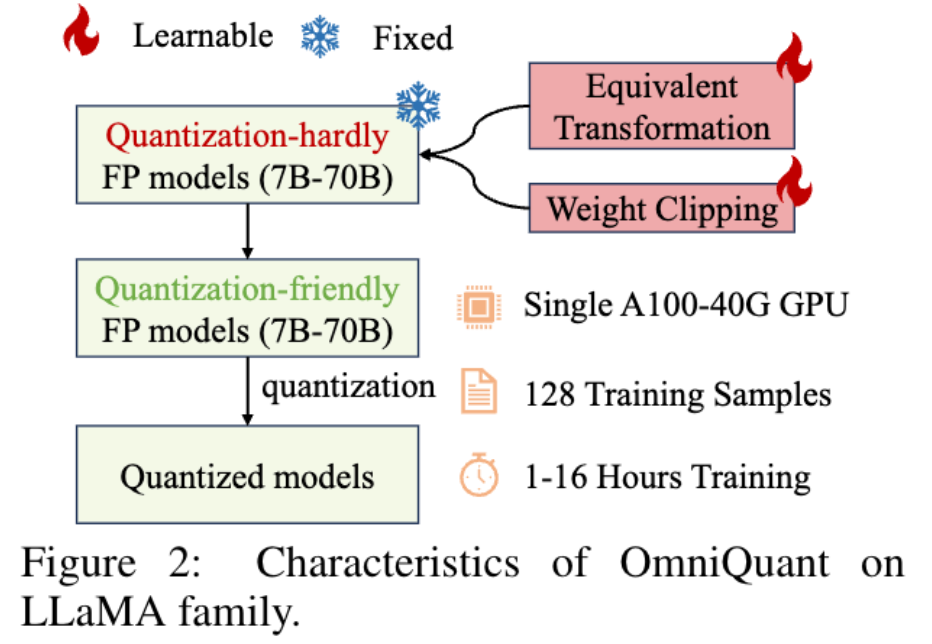
- 两大核心组件 (如图2所示):
- 可学习权重裁剪(LWC):通过优化裁剪阈值,调整权重极值,降低权重量化难度;
- 可学习等价变换(LET):在Transformer编码器中学习数学等价变换,将激活值量化的难题转移到权重上,解决激活值异常值问题。
- 块级优化框架:逐层量化Transformer块参数,基于块级误差最小化实现高效随机梯度下降(SGD)优化,且不引入额外计算或参数(裁剪阈值与等价因子可融合到量化权重中)。
1.3 OmniQuant的资源效率与性能优势
OmniQuant部署门槛低,即使资源有限也易于实现:
- 以LLaMA-2系列(70亿-700亿参数)为例,单块A100-40G GPU、128个训练样本即可完成量化,训练时间仅1-16小时(随模型规模变化);
- 性能优势显著:例如,LLaMA-13B量化为W2A16时,OmniQuant的困惑度仅13.21,而GPTQ的困惑度高达3832;W4A4量化场景下也呈现类似优势。
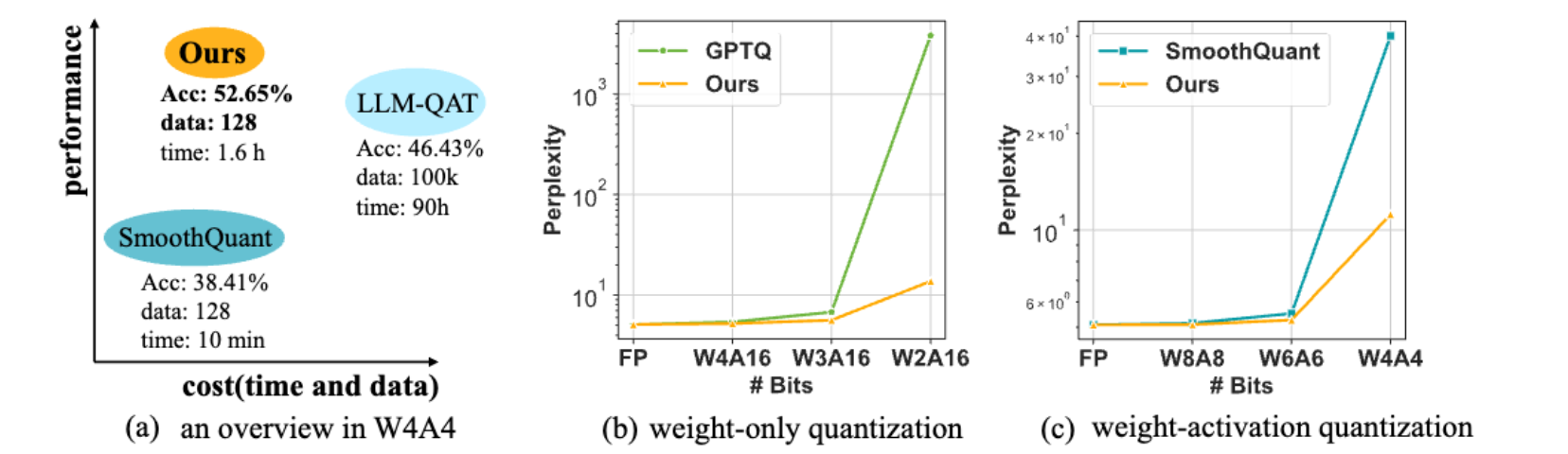
(a)W4A4量化整体情况 (b)仅权重量化 (c)权重-激活值量化
1.4 本文贡献
- 新型量化流程:提出OmniQuant框架,冻结全精度权重、引入少量可学习参数,在量化中融入梯度更新的同时保持PTQ效率;
- 核心组件创新:LWC与LET分别优化权重与激活值的量化兼容性,适配多种量化场景;
- 泛化性与实用性:在多种量化配置(W4A16、W3A16、W2A16、W6A6、W4A4)、模型系列(OPT、LLaMA、LLaMA-2、LLaMA-2-chat、Falcon)及规模(125M-180B)下均优于现有方法,且在实际设备上验证了加速与内存 reduction效果。
2 相关工作
2.1 量化方法分类
量化技术通过降低神经网络比特精度实现模型压缩与推理加速,主要分为两类:
| 方法类型 | 核心思路 | 优势 | 劣势 |
|---|---|---|---|
| 量化感知训练(QAT) | 训练过程中模拟量化,优化量化参数 | 精度高,适配复杂场景 | 训练成本极高,需全量数据与长时间训练,不适用于LLM |
| 训练后量化(PTQ) | 训练完成后对模型参数进行量化,无需重新训练 | 效率高,资源需求低 | 依赖人工设计参数,低比特场景下性能受限 |
现有PTQ方法如AdaRound(Nagel等人,2020)、BRECQ(Li等人,2021)虽通过梯度优化确定舍入方式,但需调优全量权重,无法适配数十亿参数的LLM。因此,主流LLM量化方法(Xiao等人,2023;Frantar等人,2022)优先选择"无训练PTQ",但此类方法在低比特场景下性能不足。本文目标是在LLM量化中融入梯度更新(借鉴QAT),同时保留PTQ的效率。
2.2 大型语言模型的量化方向
根据量化对象不同,LLM量化可分为仅权重量化 与权重-激活值联合量化 两类:
2.2.1 仅权重量化
专注于将权重转换为低比特,核心方法与局限如下:
- GPTQ(Frantar等人,2022):通过块级重构实现3/4比特量化,效率高但低比特性能有限;
- SpQR(Dettmers等人,2023b)、OWQ(Lee等人,2023):强调高幅度激活值相关权重的重要性,采用混合精度量化保护关键权重,但硬件兼容性差;
- AWQ(Lin等人,2023):通过通道级缩放避免混合精度的硬件低效,但依赖人工设计缩放参数;
- Qlora(Dettmers等人,2023a)、INT2.1(Chee等人,2023):通过参数高效微调恢复量化模型性能,但未直接优化量化过程。
OmniQuant与上述方法互补,通过直接优化量化过程提升性能,而非依赖微调补偿损失。
2.2.2 权重-激活值联合量化
同时压缩权重与激活值,核心方法与局限如下:
- SmoothQuant(Xiao等人,2023)、LLM.int8()(Dettmers等人,2022):通过通道级缩放或混合精度分解处理激活值异常值,实现W8A8量化,但低比特(如W4A4)性能不足;
- 异常值抑制+(Outlier Suppression+)(魏等人,2023):引入通道级偏移实现W6A6量化,但依赖人工设计参数;
- RPTQ(袁等人,2023):实现W4A4量化,但采用对部署不友好的分组激活值量化;
- LLM-QAT(Liu等人,2023b):通过QAT实现W4A4量化,但训练成本极高。
OmniQuant的优势在于:通过对部署友好的逐token量化实现W4A4量化,同时保持PTQ效率,且通过梯度优化而非人工参数提升性能。
3 OmniQuant方法
3.1 LLM量化的核心挑战
LLM量化面临两大关键难题,现有方法难以有效解决:
- 激活值量化难度高:激活值存在通道特异性异常值,尽管权重分布平坦均匀,但SmoothQuant、异常值抑制+等方法依赖预定义迁移强度或网格搜索,无法找到最优参数;
- 权重量化误差影响大:与激活值相关的权重对模型性能至关重要,但SpQR、AWQ等方法依赖人工设计的裁剪/缩放参数,在极低比特场景下误差显著。
OmniQuant通过可微量化技术 与两大创新组件解决上述问题,核心是通过灵活学习量化参数,而非依赖人工设计。
3.2 块级量化误差最小化框架
为解决传统PTQ方法(如AdaRound、BRECQ)在超大规模模型上的优化难题,OmniQuant提出块级量化误差最小化框架,逐层优化Transformer块的量化参数,而非对全量模型进行优化。
3.2.1 优化目标
框架的优化目标定义为:
arg min Θ 1 , Θ 2 ∥ F ( W , X ) − F ( Q w ( W ; Θ 1 , Θ 2 ) , Q a ( X , Θ 2 ) ) ∥ ( 1 ) \arg \min_{\Theta_{1}, \Theta_{2}} \left\| \mathcal{F}(W, X) - \mathcal{F}\left(Q_{w}\left(W ; \Theta_{1}, \Theta_{2}\right), Q_{a}\left(X, \Theta_{2}\right)\right) \right\| \quad (1) argΘ1,Θ2min∥F(W,X)−F(Qw(W;Θ1,Θ2),Qa(X,Θ2))∥(1)
其中:
- F \mathcal{F} F:LLM中Transformer块的映射函数;
- W W W、 X X X:分别为全精度权重与激活值;
- Q w ( ⋅ ) Q_{w}(\cdot) Qw(⋅)、 Q a ( ⋅ ) Q_{a}(\cdot) Qa(⋅):分别为权重量化器与激活值量化器;
- Θ 1 \Theta_{1} Θ1:可学习权重裁剪(LWC)的量化参数(如裁剪强度);
- Θ 2 \Theta_{2} Θ2:可学习等价变换(LET)的量化参数(如缩放、偏移因子)。
3.2.2 框架优势
- 多场景适配:可联合优化LWC与LET参数,同时支持仅权重量化与权重-激活值联合量化;
- 资源需求低:仅需优化少量量化参数,而非全量权重,单块A100-40G GPU、128个样本即可完成LLaMA-2系列模型量化。
3.3 可学习权重裁剪(LWC)
LWC模块通过优化裁剪强度而非直接优化裁剪阈值,降低权重量化难度,适配LLM的权重分布特性。
3.3.1 核心公式
LWC的量化过程公式如下:
W q = clamp ( ⌊ W h ⌉ + z , 0 , 2 N − 1 ) W_{q} = \text{clamp}\left(\lfloor \frac{W}{h} \rceil + z, 0, 2^{N} - 1\right) Wq=clamp(⌊hW⌉+z,0,2N−1)
其中:
- h = γ ⋅ max ( W ) − β ⋅ min ( W ) 2 N − 1 h = \frac{\gamma \cdot \max(W) - \beta \cdot \min(W)}{2^{N} - 1} h=2N−1γ⋅max(W)−β⋅min(W)(权重归一化因子);
- z = − ⌊ β ⋅ min ( W ) h ⌉ z = -\left\lfloor \frac{\beta \cdot \min(W)}{h} \right\rceil z=−⌊hβ⋅min(W)⌉(零点值);
- ⌊ ⋅ ⌉ \lfloor \cdot \rceil ⌊⋅⌉:舍入操作;
- N N N:目标量化比特数;
- γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ∈[0,1]、 β ∈ [ 0 , 1 ] \beta \in [0,1] β∈[0,1]:可学习裁剪强度(分别控制权重上界与下界的裁剪比例,通过sigmoid函数实例化,确保取值在合理范围);
- clamp \text{clamp} clamp:将量化后权重约束在 [ 0 , 2 N − 1 ] [0, 2^{N} - 1] [0,2N−1](N比特整数范围)。
3.3.2 关键特性
- 兼容性强 :当 γ = 1 \gamma=1 γ=1且 β = 1 \beta=1 β=1时,退化为传统MinMax量化,可无缝适配现有PTQ流程;
- 优化难度低 :仅需调整裁剪强度 γ \gamma γ、 β \beta β即可确定最优裁剪阈值,无需优化全量权重;
- 性能优势:通过最优阈值裁剪,权重极值被合理调整,量化误差显著降低(实验表明,LWC在仅权重量化场景下显著优于GPTQ、AWQ等方法,见表1)。
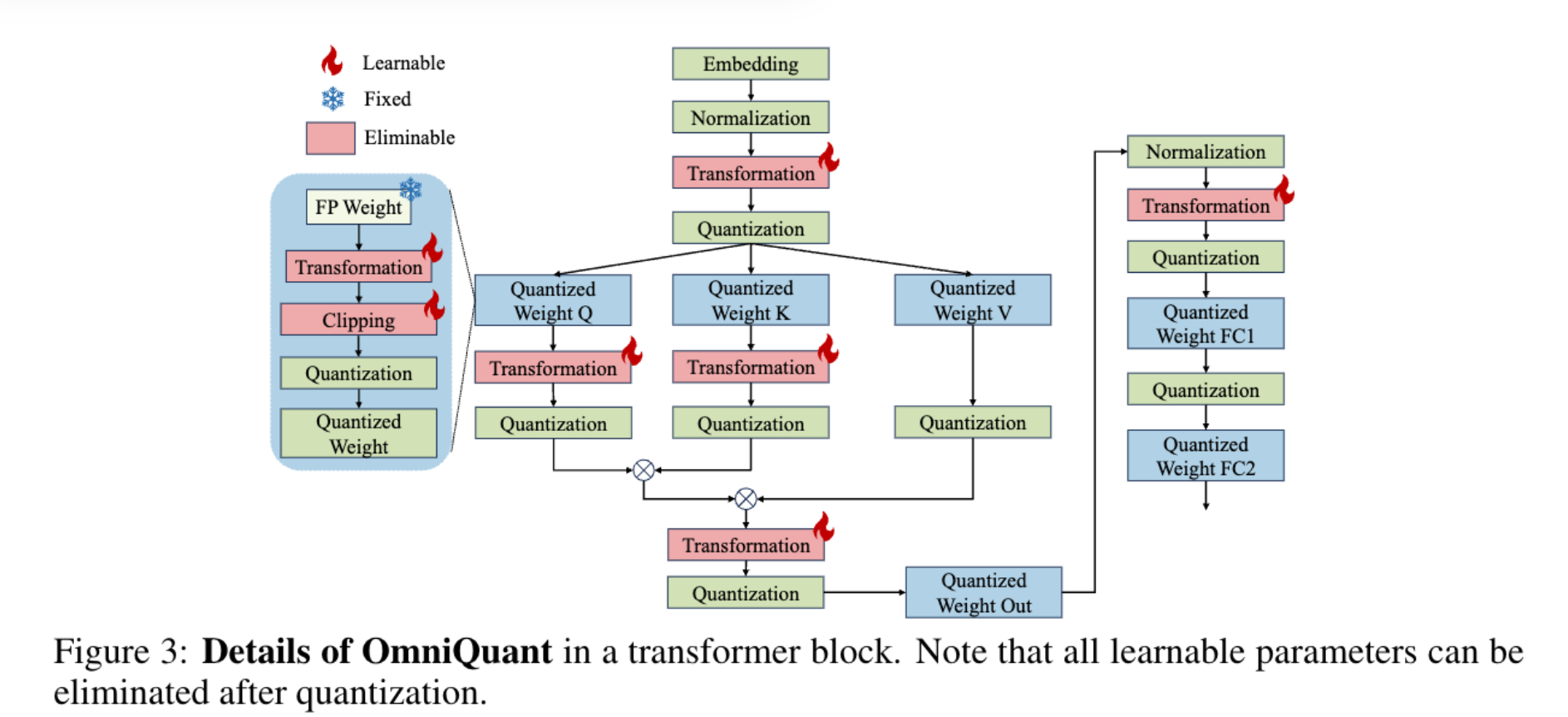
3.4 可学习等价变换(LET)
LET模块通过数学等价变换,将激活值量化的难题转移到权重上(权重可通过LWC进一步优化),解决激活值异常值问题。
3.4.1 核心思路
激活值异常值具有通道特异性,LET通过通道级缩放( s s s) 与通道级偏移( δ \delta δ) 调整激活值分布,同时保证变换前后模型输出等价(数学严谨性)。LET分别在线性层 与注意力操作中实现,覆盖LLM的核心计算模块。
3.4.2 线性层的等价变换
线性层的输入为 X ∈ R T × C i n X \in \mathbb{R}^{T \times C_{in}} X∈RT×Cin( T T T为token长度, C i n C_{in} Cin为输入通道数),输出为权重矩阵 W ∈ R C i n × C o u t W \in \mathbb{R}^{C_{in} \times C_{out}} W∈RCin×Cout与偏置 B ∈ R 1 × C o u t B \in \mathbb{R}^{1 \times C_{out}} B∈R1×Cout的乘积。LET的等价变换公式如下:
Y = X W + B = ( X − δ ) ⊘ s ⏟ X ^ ⋅ s ⊙ W ⏟ W ^ + B + δ W ⏟ B ^ ( 3 ) Y = XW + B = \underbrace{(X - \delta) \oslash s}{\hat{X}} \cdot \underbrace{s \odot W}{\hat{W}} + \underbrace{B + \delta W}_{\hat{B}} \quad (3) Y=XW+B=X^ (X−δ)⊘s⋅W^ s⊙W+B^ B+δW(3)
其中:
- X ^ \hat{X} X^、 W ^ \hat{W} W^、 B ^ \hat{B} B^:分别为变换后的等价激活值、权重、偏置;
- ⊘ \oslash ⊘、 ⊙ \odot ⊙:分别为元素级除法与乘法;
- s s s、 δ \delta δ:通道级可学习参数(分别控制缩放与偏移,通过块级误差最小化优化)。
量化过程 :对变换后的 X ^ \hat{X} X^(激活值)与 W ^ \hat{W} W^(权重)进行量化,公式如下:
Y = Q a ( X ^ ) Q w ( W ^ ) + B ^ ( 4 ) Y = Q_{a}(\hat{X}) Q_{w}(\hat{W}) + \hat{B} \quad (4) Y=Qa(X^)Qw(W^)+B^(4)
其中, Q a Q_{a} Qa为标准MinMax量化器, Q w Q_{w} Qw为融合LWC的MinMax量化器(确保权重适配量化)。
关键特性 :变换参数( s s s、 δ \delta δ)可融入前序归一化层或线性层,不引入额外计算或参数;仅排除FFN的第二个线性层(因非线性层后特征稀疏度高,易导致梯度不稳定)。
3.4.3 注意力操作的等价变换
注意力操作占LLM计算量的重要比例,且自回归特性需存储KV缓存(长序列场景内存需求高)。LET通过等价变换优化Q/K矩阵的量化,公式如下:
P = Softmax ( Q K T ) = Softmax ( Q ⊘ s a ⏟ Q ^ ⋅ s a ⊙ K T ⏟ K ^ T ) ( 5 ) P = \text{Softmax}(QK^{T}) = \text{Softmax}\left( \underbrace{Q \oslash s_{a}}{\hat{Q}} \cdot \underbrace{s{a} \odot K^{T}}_{\hat{K}^{T}} \right) \quad (5) P=Softmax(QKT)=Softmax Q^ Q⊘sa⋅K^T sa⊙KT (5)
其中:
- s a ∈ R 1 × C o u t s_{a} \in \mathbb{R}^{1 \times C_{out}} sa∈R1×Cout:注意力亲和矩阵的可学习缩放因子;
- Q ^ \hat{Q} Q^、 K ^ T \hat{K}^{T} K^T:变换后的等价Q矩阵与K矩阵转置。
量化过程 :对 Q ^ \hat{Q} Q^、 K ^ T \hat{K}^{T} K^T采用MinMax量化,公式如下:
P = Softmax ( Q a ( Q ^ ) Q a ( K ^ T ) ) P = \text{Softmax}(Q_{a}(\hat{Q}) Q_{a}(\hat{K}^{T})) P=Softmax(Qa(Q^)Qa(K^T))
关键特性 : s a s_{a} sa可融入查询/键投影的线性权重;无需对V矩阵显式变换(其分布已通过输出投影层的逆变换调整)。
4 实验
4.1 实验设置
4.1.1 量化配置
| 量化类型 | 默认设置 | 说明 |
|---|---|---|
| 仅权重量化 | INT4/INT3/INT2 通道级量化;分组量化用"g"标识(如W3A16g128表示128分组的3比特仅权重量化) | 仅量化权重,激活值保持全精度 |
| 权重-激活值联合量化 | INT6/INT4 通道级权重量化 + 逐token激活值量化 | 所有中间激活值量化为低比特,SoftMax输出因长尾分布保持全精度 |
4.1.2 训练参数
- 参数初始化:通道级缩放因子用SmoothQuant初始化,偏移因子用异常值抑制+初始化;
- 优化器:AdamW(权重衰减=0);
- 学习率:LWC为5e-3,LET为1e-2;
- 校准数据:128个随机选取的2048-token WikiText2片段(Merity等人,2016);
- 训练环境:单块NVIDIA A100 GPU,批大小=1,训练轮次=20(W2A16量化为40轮);
- 组件启用规则:权重-激活值量化启用LWC+LET;仅权重量化中,OPT启用LWC+LET,LLaMA仅启用LWC(LET对LLaMA提升微弱,见表A3)。
4.1.3 模型与评估
- 测试模型:OPT(125M-66B)、LLaMA(7B-65B)、LLaMA-2(7B-70B)、Falcon-180B、指令微调模型LLaMA-2-chat(验证泛化性);
- 评估指标 :
- 语言生成:WikiText2(Merity等人,2016)、PTB(Marcus等人,1994)、C4(Raffel等人,2020)数据集的困惑度(Perplexity,越低越好);
- 零样本任务:PIQA(Bisk等人,2020)、ARC(Clark等人,2018)、BoolQ(Clark等人,2019)、HellaSwag(Clark等人,2018)的准确率(越高越好);
- 基线方法 :
- 仅权重量化:RTN(标准舍入量化)、GPTQ、AWQ;
- 权重-激活值量化:SmoothQuant、异常值抑制+(OS+)、RPTQ、LLM-QAT(QAT方法)。
4.2 仅权重量化结果
LLaMA系列模型的仅权重量化结果见表1(WikiText2困惑度),OPT模型结果见附录A8。核心结论如下:
4.2.1 泛化性强
OmniQuant在多种量化配置(W2A16、W2A16g128、W2A16g64、W3A16、W3A16g128、W4A16、W4A16g128)与模型系列(OPT、LLaMA-1、LLaMA-2)下均持续优于基线方法。例如:
- W2A16配置下,LLaMA-1-13B的OmniQuant困惑度为13.21,而GPTQ为55.91、AWQ为2.8e5;
- W3A16g128配置下,LLaMA-2-70B的OmniQuant困惑度为3.78,而GPTQ为3.85、AWQ为-(未报告)。
4.2.2 低比特场景优势显著
量化比特数越低,OmniQuant的性能优势越明显。例如:
- W2A16(2比特权重)配置下,LLaMA-1-7B的OmniQuant困惑度为15.47,而GPTQ为2.1e3、RTN为1.1e5;
- W3A16(3比特权重)配置下,LLaMA-1-30B的OmniQuant困惑度为4.74,而GPTQ为5.84、AWQ为10.07。
4.2.3 适配多种量化方式
AWQ在分组量化中表现较好,但OmniQuant在通道级与分组量化中均优于基线。例如:
- W2A16g64(64分组)配置下,LLaMA-1-13B的OmniQuant困惑度为7.34,而GPTQ为10.06、AWQ为2.7e5;
- W4A16g128(128分组)配置下,LLaMA-2-13B的OmniQuant困惑度为4.95,而GPTQ为4.98、AWQ为4.97。
表1:LLaMA-1与LLaMA-2模型仅权重量化结果(WikiText2困惑度,越低越好)
(注:C4数据集困惑度见附录表A19)
| LLaMA1&2 / 困惑度(↓) | 配置 | 方法 | 1-7B(FP16:5.68) | 1-13B(FP16:5.09) | 1-30B(FP16:4.10) | 1-65B(FP16:3.53) | 2-7B(FP16:5.47) | 2-13B(FP16:4.88) | 2-70B(FP16:3.31) |
|---|---|---|---|---|---|---|---|---|---|
| W2A16 | RTN | 1.1e5 | 6.8e4 | 2.4e4 | 2.2e4 | 3.8e4 | 5.6e4 | 2.0e4 | |
| GPTQ | 2.1e3 | 5.5e3 | 499.75 | 55.91 | 2.1e3 | - | 77.95 | ||
| OmniQuant | 15.47 | 13.21 | 8.71 | 7.58 | 37.37 | 17.21 | 7.81 | ||
| W2A16 g128 | RTN | 1.9e3 | 781.20 | 68.04 | 15.08 | 4.2e3 | 122.08 | 27.27 | |
| GPTQ | 44.01 | 15.60 | 10.92 | 9.51 | 36.77 | 28.14 | NAN | ||
| AWQ | 2.6e5 | 2.8e5 | 2.4e5 | 7.4e4 | 2.2e5 | 1.2e5 | - | ||
| OmniQuant | 9.72 | 7.93 | 7.12 | 5.95 | 11.06 | 8.26 | 6.55 | ||
| W2A16 g64 | RTN | 188.32 | 101.87 | 19.20 | 9.39 | 431.97 | 26.22 | 10.31 | |
| GPTQ | 22.10 | 10.06 | 8.54 | 8.31 | 20.85 | 22.44 | NAN | ||
| AWQ | 2.5e5 | 2.7e5 | 2.3e5 | 7.4e4 | 2.1e5 | 1.2e5 | - | ||
| OmniQuant | 8.90 | 7.34 | 6.59 | 5.65 | 9.62 | 7.56 | 6.11 | ||
| W3A16 | RTN | 25.73 | 11.39 | 14.95 | 10.68 | 539.48 | 10.68 | 7.52 | |
| GPTQ | 8.06 | 6.76 | 5.84 | 5.06 | 8.37 | 6.44 | 4.82 | ||
| AWQ | 11.88 | 7.45 | 10.07 | 5.21 | 24.00 | 10.45 | - | ||
| OmniQuant | 6.49 | 5.68 | 4.74 | 4.04 | 6.58 | 5.58 | 3.92 | ||
| W3A16 g128 | RTN | 7.01 | 5.88 | 4.87 | 4.24 | 6.66 | 5.51 | 3.97 | |
| GPTQ | 6.55 | 5.62 | 4.80 | 4.17 | 6.29 | 5.42 | 3.85 | ||
| AWQ | 6.46 | 5.51 | 4.63 | 3.99 | 6.24 | 5.32 | - | ||
| OmniQuant | 6.15 | 5.44 | 4.56 | 3.94 | 6.03 | 5.28 | 3.78 | ||
| W4A16 | RTN | 6.43 | 5.55 | 4.57 | 3.87 | 6.11 | 5.20 | 3.67 | |
| GPTQ | 6.13 | 5.40 | 4.48 | 3.83 | 5.83 | 5.13 | 3.58 | ||
| AWQ | 6.08 | 5.34 | 4.39 | 3.76 | 6.15 | 5.12 | - | ||
| OmniQuant | 5.86 | 5.21 | 4.25 | 3.71 | 5.74 | 5.02 | 3.47 | ||
| W4A16 g128 | RTN | 5.96 | 5.25 | 4.23 | 3.67 | 5.72 | 4.98 | 3.46 | |
| GPTQ | 5.85 | 5.20 | 4.23 | 3.65 | 5.61 | 4.98 | 3.42 | ||
| AWQ | 5.81 | 5.20 | 4.21 | 3.62 | 5.62 | 4.97 | - | ||
| OmniQuant | 5.77 | 5.17 | 4.19 | 3.62 | 5.58 | 4.95 | 3.40 |
4.3 权重-激活值联合量化结果
实验重点关注W6A6(6比特权重、6比特激活值)与W4A4(4比特权重、4比特激活值)配置(W8A8配置下SmoothQuant已接近无损,无需对比)。LLaMA系列模型的零样本任务准确率结果见表2,困惑度结果见附录A23、A24,OPT模型结果见附录A25。核心结论如下:
4.3.1 显著提升低比特性能
W4A4(极低比特)配置下,OmniQuant的平均准确率比基线方法提升4.99%-11.80%。例如:
- LLaMA-1-7B:OmniQuant平均准确率为52.65%,而SmoothQuant为38.41%、LLM-QAT+SQ为46.43%、OS+为48.43%;
- LLaMA-1-65B:OmniQuant平均准确率为59.22%,而SmoothQuant为47.71%、OS+为52.52%。
4.3.2 超越QAT方法
在LLaMA-1-7B的W4A4配置下,OmniQuant的平均准确率(52.65%)比LLM-QAT(QAT方法,41.27%)高11.38%,比LLM-QAT+SQ(46.43%)高6.22%,证明"少量可学习量化参数+PTQ效率"的策略优于"全量权重优化+QAT高成本"。
4.3.3 W6A6配置下保持高精度
W6A6(中比特)配置下,OmniQuant的性能接近全精度模型,且优于基线方法。例如:
- LLaMA-1-30B:OmniQuant平均准确率为67.23%,仅比全精度模型(67.44%)低0.21%,而SmoothQuant为65.20%、OS+为67.01%;
- LLaMA-1-65B:OmniQuant平均准确率为70.28%,比全精度模型(71.04%)低0.76%,而SmoothQuant为69.80%、OS+为68.76%。
表2:LLaMA模型权重-激活值联合量化结果(6个零样本任务准确率,越高越好)
(注:困惑度结果见附录表A23、A24)
| LLaMA / 准确率(↑) | 比特数 | 方法 | PIQA | ARC-e | ARC-c | BoolQ | HellaSwag | Winogrande | 平均值 |
|---|---|---|---|---|---|---|---|---|---|
| LLaMA-1-7B | FP16 | - | 77.47 | 52.48 | 41.46 | 73.08 | 73.00 | 67.07 | 64.09 |
| W6A6 | SmoothQuant | 76.75 | 51.64 | 39.88 | 71.75 | 71.67 | 65.03 | 62.81 | |
| W6A6 | OS+ | 76.82 | 51.35 | 41.13 | 72.08 | 71.42 | 65.98 | 61.13 | |
| W6A6 | OmniQuant | 77.09 | 51.89 | 40.87 | 72.53 | 71.61 | 65.03 | 63.17 | |
| W4A4 | SmoothQuant | 49.80 | 30.40 | 25.80 | 49.10 | 27.40 | 48.00 | 38.41 | |
| W4A4 | LLM-QAT | 51.50 | 27.90 | 23.90 | 61.30 | 31.10 | 51.90 | 41.27 | |
| W4A4 | LLM-QAT+SQ | 55.90 | 35.50 | 26.40 | 62.40 | 47.80 | 50.60 | 46.43 | |
| W4A4 | OS+ | 62.73 | 39.98 | 30.29 | 60.21 | 44.39 | 52.96 | 48.43 | |
| W4A4 | OmniQuant | 66.15 | 45.20 | 31.14 | 63.51 | 56.44 | 53.43 | 52.65 | |
| LLaMA-1-13B | FP16 | - | 79.10 | 59.89 | 44.45 | 68.01 | 76.21 | 70.31 | 66.33 |
| W6A6 | SmoothQuant | 77.91 | 56.60 | 42.40 | 64.95 | 75.36 | 69.36 | 64.43 | |
| W6A6 | OS+ | 78.29 | 56.90 | 43.09 | 66.98 | 75.09 | 69.22 | 64.92 | |
| W6A6 | OmniQuant | 78.40 | 57.28 | 42.91 | 67.00 | 75.82 | 68.27 | 64.95 | |
| W4A4 | SmoothQuant | 61.04 | 39.18 | 30.80 | 61.80 | 52.29 | 51.06 | 49.36 | |
| W4A4 | OS+ | 63.00 | 40.32 | 30.38 | 60.34 | 53.61 | 51.54 | 49.86 | |
| W4A4 | OmniQuant | 69.69 | 47.39 | 33.10 | 62.84 | 58.96 | 55.80 | 54.37 | |
| LLaMA-1-30B | FP16 | - | 80.08 | 58.92 | 45.47 | 68.44 | 79.21 | 72.53 | 67.44 |
| W6A6 | SmoothQuant | 77.14 | 57.61 | 42.91 | 65.56 | 78.07 | 69.92 | 65.20 | |
| W6A6 | OS+ | 80.14 | 58.92 | 45.05 | 68.02 | 77.96 | 71.98 | 67.01 | |
| W6A6 | OmniQuant | 79.81 | 58.79 | 45.22 | 68.38 | 78.95 | 72.21 | 67.23 | |
| W4A4 | SmoothQuant | 58.65 | 35.53 | 27.73 | 60.42 | 35.56 | 48.06 | 44.83 | |
| W4A4 | OS+ | 67.63 | 46.17 | 34.40 | 60.70 | 54.32 | 52.64 | 52.62 | |
| W4A4 | OmniQuant | 71.21 | 49.45 | 34.47 | 65.33 | 64.65 | 59.19 | 56.63 | |
| LLaMA-1-65B | FP16 | - | 80.79 | 58.71 | 46.24 | 82.29 | 80.72 | 77.50 | 71.04 |
| W6A6 | SmoothQuant | 80.25 | 57.92 | 45.50 | 80.22 | 80.18 | 74.76 | 69.80 | |
| W6A6 | OS+ | 79.67 | 55.68 | 45.22 | 80.02 | 78.03 | 73.95 | 68.76 | |
| W6A6 | OmniQuant | 81.01 | 58.12 | 46.33 | 80.64 | 79.91 | 75.69 | 70.28 | |
| W4A4 | SmoothQuant | 64.47 | 40.44 | 29.82 | 59.38 | 39.90 | 52.24 | 47.71 | |
| W4A4 | OS+ | 68.06 | 43.98 | 35.32 | 62.75 | 50.73 | 54.30 | 52.52 | |
| W4A4 | OmniQuant | 71.81 | 48.02 | 35.92 | 73.27 | 66.81 | 59.51 | 59.22 |
4.4 指令微调模型的量化结果
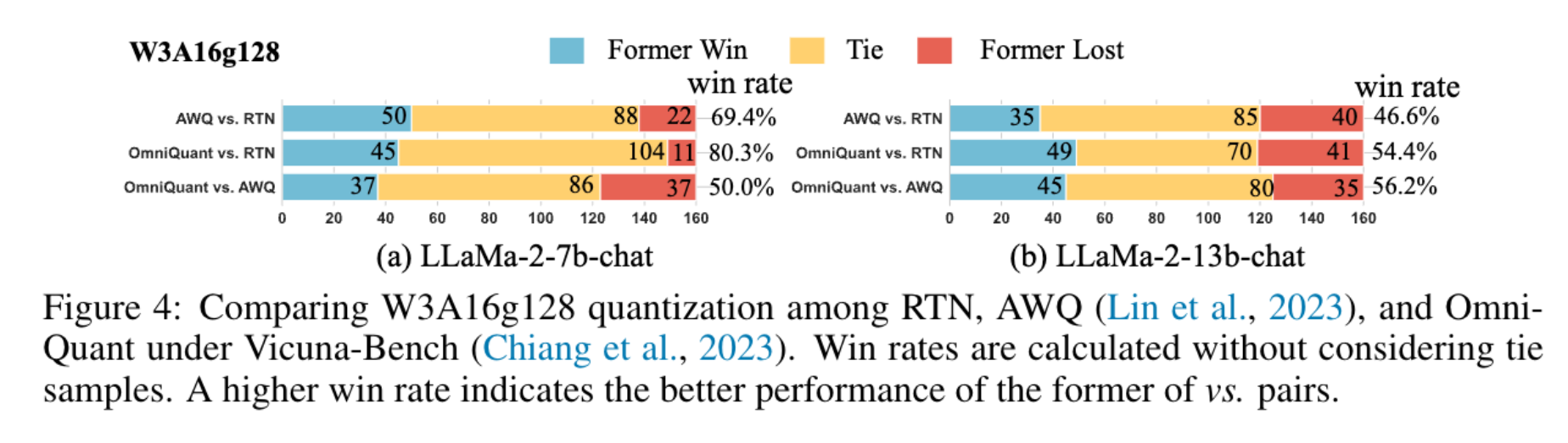
为验证OmniQuant的泛化性,实验在指令微调模型LLaMA-2-chat上进行,采用GPT-4评估协议(Chiang等人,2023),在包含80个问题的Vicuna基准(Chiang等人,2023)上测试,每个对比对进行160次试验(消除位置偏差)。结果如图4所示,核心结论如下:
4.4.1 LLaMA-2-7B-chat
- OmniQuant与AWQ对RTN的胜率分别为80.3%与69.4%,OmniQuant显著优于RTN;
- OmniQuant与AWQ的胜率为50%,两者性能相当,但OmniQuant资源效率更高。
4.4.2 LLaMA-2-13B-chat
- AWQ对RTN的胜率仅46.6%(性能倒退),而OmniQuant对RTN的胜率为56.2%、对AWQ的胜率为54.4%,持续提升量化模型性能。
4.5 实际设备上的推理加速
实验基于MLC-LLM(https://github.com/mlc-ai/mlc-llm)部署,验证OmniQuant在NVIDIA A100-80G GPU上的内存占用与推理速度(生成512个token的耗时)。结果见表3,核心结论如下:
4.5.1 显著降低内存占用
量化模型的权重内存(WM)与运行内存(RM)均远低于FP16全精度模型。例如:
- LLaMA-2-70B:W4A16g128配置的WM为33.0G、RM为41.0G,而FP16的WM为60.6G、RM为66.1G(内存占用降低约40%);
- LLaMA-2-7B:W2A16g128配置的WM为2.2G、RM为4.1G,而FP16的WM为12.6G、RM为14.4G(内存占用降低约70%)。
4.5.2 大幅提升推理速度
低比特量化模型的推理速度接近FP16模型的2倍。例如:
- LLaMA-2-7B:W4A16g128配置的推理速度为134.2 token/s,而FP16为69.2 token/s(提速约94%);
- LLaMA-2-13B:W2A16g128配置的推理速度为92.6 token/s,而FP16为52.5 token/s(提速约76%)。
4.5.3 硬件兼容性
OmniQuant不引入额外操作,可无缝适配MLC-LLM;但当前MLC-LLM对INT3/INT2的支持尚不完善(尤其是INT3),未来将优化低比特推理速度。
表3:基于MLC-LLM的仅权重量化部署结果(NVIDIA A100-80G,WM=权重内存,RM=运行内存,token/s=推理速度)
| LLaMA | 配置 | 7B - WM | 7B - RM | 7B - token/s | 13B - WM | 13B - RM | 13B - token/s | 30B - WM | 30B - RM | 30B - token/s | 65B - WM | 65B - RM | 65B - token/s |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FP16 | - | 12.6G | 14.4G | 69.2 | 24.3G | 27.1G | 52.5 | 60.6G | 66.1G | 23.9 | - | OOM | - |
| W4A16g128 | - | 3.8G | 5.7G | 134.2 | 7.0G | 10.0G | 91.3 | 16.7G | 21.7G | 43.6 | 33.0G | 41.0G | 24.3 |
| W3A16g128 | - | 3.2G | 5.1G | 83.4 | 5.8G | 8.7G | 57.6 | 13.7G | 18.7G | 29.0 | 27.0G | 35.1G | 15.2 |
| W2A16g128 | - | 2.2G | 4.1G | 83.9 | 4.0G | 7.5G | 92.6 | 9.2G | 14.1G | 36.7 | 18.0G | 25.6G | 24.8 |
5 结论
本文提出OmniQuant技术,推动仅权重量化与权重-激活值联合量化向低比特格式发展,核心贡献与优势总结如下:
- 核心原则:冻结原始全精度权重,引入少量可学习量化参数,在量化中融入梯度更新的同时保持PTQ的时间与数据效率;
- 创新组件 :
- 可学习权重裁剪(LWC):通过优化裁剪强度调整权重极值,降低权重量化难度;
- 可学习等价变换(LET):通过数学等价变换将激活值量化难题转移到权重上,解决激活值异常值问题;
- 性能优势:在多种量化配置、模型系列与规模下均优于现有方法,尤其在极低比特(W2A16、W4A4)场景下优势显著;
- 实用性强:适配指令微调模型,且在实际设备上显著降低内存占用、提升推理速度,硬件兼容性好(可学习参数可融合到量化权重中,无额外开销)。
未来工作将进一步优化INT3/INT2量化的硬件支持,提升极低比特场景的推理速度。
致谢
本研究部分受中国国家重点研发计划(项目编号:2022ZD0161000)与香港研究资助局通用研究基金(项目编号:17200622)支持。感谢商汤科技的刘文涛博士提供LLM部署相关的宝贵建议,感谢Apache TVM的冯思源博士协助在MLC-LLM项目中部署OmniQuant。
附录(节选)
A1 OmniQuant算法伪代码
OmniQuant的完整训练算法通过块级校准实现,包含三个核心步骤:可学习参数初始化、参数训练、模型变换与量化。伪代码如下:
算法1:OmniQuant整体算法
输入:校准数据集X、预训练LLM模型M
输出:量化后的模型
1: Xfp = Xq = X # 初始化全精度与量化模型的输入
2: for Bi in M do: # 块级校准(逐Transformer块处理)
3: Xfp = Bi(Xfp) # 更新全精度模型的输入
4: 初始化可学习权重裁剪参数Θ1
5: 初始化可学习等价变换参数Θ2
6: for k in 训练轮次 do: # 训练可学习参数
7: for (xq, xfp) in (Xq, Xfp) do:
8: B'i = 基于LWC的量化(Bi, Θ1) # 公式(2)
9: B'i = 基于LET的变换(B'i, Θ2) # 公式(3)(5)
10: x'q = B'i(xq) # 量化模型的输出
11: loss = ||xfp - x'q||² # 块级误差(公式(1))
12: loss.backward() # 反向传播计算梯度
13: end for
14: 通过梯度更新Θ1与Θ2 # SGD优化
15: end for
16: Bi = 基于LET的变换(Bi, Θ2) # 应用学到的等价变换
17: Bi = 基于LWC的量化(Bi, Θ1) # 量化当前块
18: Xq = Bi(Xq) # 更新量化模型的输入
19: end for
20: return 量化后的模型MA2 与现有等价变换方法的区别
OmniQuant的LET与SmoothQuant、AWQ、异常值抑制+(OS+)的核心区别见表A1,主要优势在于:
- 操作更全面:同时支持通道级缩放与偏移,而SmoothQuant、AWQ仅支持缩放;
- 覆盖范围广:同时优化线性层与注意力操作,而现有方法仅覆盖线性层;
- 参数优化优:通过梯度优化确定等价参数,而现有方法依赖预定义或网格搜索;
- 场景适配多:同时支持仅权重量化与权重-激活值联合量化,而现有方法仅适配单一场景。
表A1:现有等价变换方法的区别对比
| 方法 | 等价变换操作 | 变换位置 | 参数获取方式 | 适用场景 |
|---|---|---|---|---|
| SmoothQuant | 通道级缩放 | 线性层 | 预定义迁移强度 | 权重-激活值联合量化 |
| AWQ | 通道级缩放 | 线性层 | 网格搜索 | 仅权重量化 |
| OS+ | 通道级缩放+偏移 | 线性层 | 缩放(网格搜索)、偏移(预定义) | 权重-激活值联合量化 |
| OmniQuant | 通道级缩放+偏移 | 线性层+注意力 | 梯度优化 | 仅权重量化+权重-激活值联合量化 |
A3 消融实验(节选)
A3.1 LWC与LET的协同作用
实验验证LWC与LET的组合效果,结果见表A2。核心结论:
- LET与LWC联合训练的性能最优(平均困惑度12.87、平均准确率52.65%),显著优于其他组合(如LET+网格搜索裁剪、SmoothQuant+LWC);
- 协同作用源于LET将激活值量化难题转移到权重,LWC进一步优化权重适配量化,形成"迁移-优化"的闭环。
表A2:等价变换与权重裁剪的组合效果(LLaMA-7B W4A4配置)
| 方法 | 平均困惑度(↓) | 平均准确率(↑) |
|---|---|---|
| SmoothQuant | 28.78 | 38.41% |
| LET | 16.97 | 48.83% |
| LET + 网格搜索裁剪 | 15.82 | 49.59% |
| SmoothQuant + LWC | 15.80 | 50.15% |
| LET + LWC(OmniQuant) | 12.87 | 52.65% |
A3.2 训练数据效率
实验验证校准样本数量对OmniQuant性能的影响,结果见表A11。核心结论:
- OmniQuant在仅16个样本时即可收敛(LLaMA-7B W3A16配置的WikiText2困惑度为6.47,与128个样本的6.47一致);
- 128个样本为最优选择,与现有方法(GPTQ、AWQ)保持一致,兼顾性能与效率。
表A11:校准样本数量的消融实验(LLaMA-7B)
| 样本数量 | W3A16 - WikiText2困惑度 | W3A16 - C4困惑度 | W4A4 - WikiText2困惑度 | W4A4 - C4困惑度 |
|---|---|---|---|---|
| 16 | 6.47 | 8.18 | 11.56 | 14.84 |
| 32 | 6.47 | 8.18 | 11.48 | 14.80 |
| 64 | 6.48 | 8.19 | 11.40 | 14.57 |
| 128 | 6.47 | 8.19 | 11.23 | 14.61 |
| 256 | 6.46 | 8.19 | 11.41 | 14.90 |
A4 LLaMA系列模型的训练时间
实验在单块NVIDIA A100-80G GPU上进行,校准数据为128个2048-token WikiText2片段,训练轮次20轮,结果见表A12。核心结论:
- 训练时间随模型规模增长而增加,但均在合理范围(7B为1.1-1.6小时,70B为8.9-14.4小时);
- 权重-激活值量化的训练时间略长于仅权重量化(需同时优化LWC与LET),但仍远低于QAT方法(数百GPU小时)。
表A12:OmniQuant在LLaMA系列模型上的训练时间
| LLaMA | 7B | 13B | 30B | 65B |
|---|---|---|---|---|
| 仅权重量化 | 1.1小时 | 2.2小时 | 4.5小时 | 8.9小时 |
| 权重-激活值量化 | 1.6小时 | 3.3小时 | 7.3小时 | 14.4小时 |
A8 完整实验结果(节选)
A8.1 Falcon-180B的仅权重量化结果
Falcon-180B是超大规模LLM,实验验证OmniQuant在该模型上的性能,结果见表A18。核心结论:
- W3A16g512配置下,OmniQuant的WikiText2困惑度为3.71(接近FP16的3.29),而RTN为5.33;
- 零样本任务准确率方面,OmniQuant的平均准确率为79.40%,仅比FP16(80.58%)低1.18%,而RTN为77.97%。
表A18:Falcon-180B仅权重量化结果(W3A16g512配置)
| 方法 | 比特数配置 | 内存占用 | 部署设备 | WikiText2困惑度 | PTB困惑度 | C4困惑度 | PIQA准确率 | ARC-e准确率 | ARC-c准确率 | BoolQ准确率 | HellaSwag准确率 | Winogrande准确率 | 平均准确率 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FP16 | BF16/FP16 | 335GB | 5×A100-80G | 3.29 | 6.64 | 6.31 | 84.82% | 84.20% | 60.83% | 86.85% | 85.91% | 80.58% | 80.58% |
| RTN | W3A16g512 | 65GB | 1×A100-80G | 5.33 | 8.08 | 8.34 | 83.48% | 80.85% | 55.46% | 78.37% | 81.05% | 77.97% | 77.97% |
| OmniQuant | W3A16g512 | 65GB | 1×A100-80G | 3.71 | 6.95 | 6.71 | 84.71% | 82.91% | 60.92% | 84.03% | 84.96% | 79.40% | 79.40% |
参考文献(节选)
- Bubeck, S., Chandrasekaran, V., Eldan, R., et al. (2023). Sparks of artificial general intelligence: Early experiments with GPT-4. arXiv preprint arXiv:2303.12712.
- Brown, T., Mann, B., Ryder, N., et al. (2020). Language models are few-shot learners. Advances in Neural Information Processing Systems, 33, 1877--1901.
- Frantar, E., Ashkboos, S., Hoefler, T., & Alistarh, D. (2022). GPTQ: Accurate post-training quantization for generative pre-trained transformers. arXiv preprint arXiv:2210.17323.
- Lin, J., Tang, J., Tang, H., et al. (2023). AWQ: Activation-aware weight quantization for LLM compression and acceleration. arXiv preprint arXiv:2306.0098.
- Xiao, G., Lin, J., Seznec, M., et al. (2023). SmoothQuant: Accurate and efficient post-training quantization for large language models. In International Conference on Machine Learning (pp. 38087--38099). PMLR.
- Touvron, H., Lavril, T., Izacard, G., et al. (2023a). LLaMA: Open and efficient foundation language models. arXiv preprint arXiv:2302.13971.
- Touvron, H., Martin, L., Stone, K., et al. (2023b). LLaMA 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288.