前置知识:
三角函数,函数图像及性质
声音的本质:
声音是由于物体的振动产生的能引起听觉的波。声音的振动其本质就是物体在某一中心位置循环往复的运动(类似的还有弹簧的振动,钟摆的摆动等)。在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为"简谐运动"。可以证明,在适当的直角坐标系下,简谐运动可以用函数,
,其中A>0,w>0。每一个音都是由纯音合成的,纯音的数学模型是
.音有四要素:音调,响度,音长,音色。这都与正弦函数的参数有关。
正弦函数的参数与声音的关系:
响度与振幅:
振幅即A,它是做简谐运动的物体离开平衡位置的最大距离(表示成图像,就是图像的最值)
振幅越大,声波携带的能量越高,导致响度增加。两者呈正相关关系,但并非线性比例。
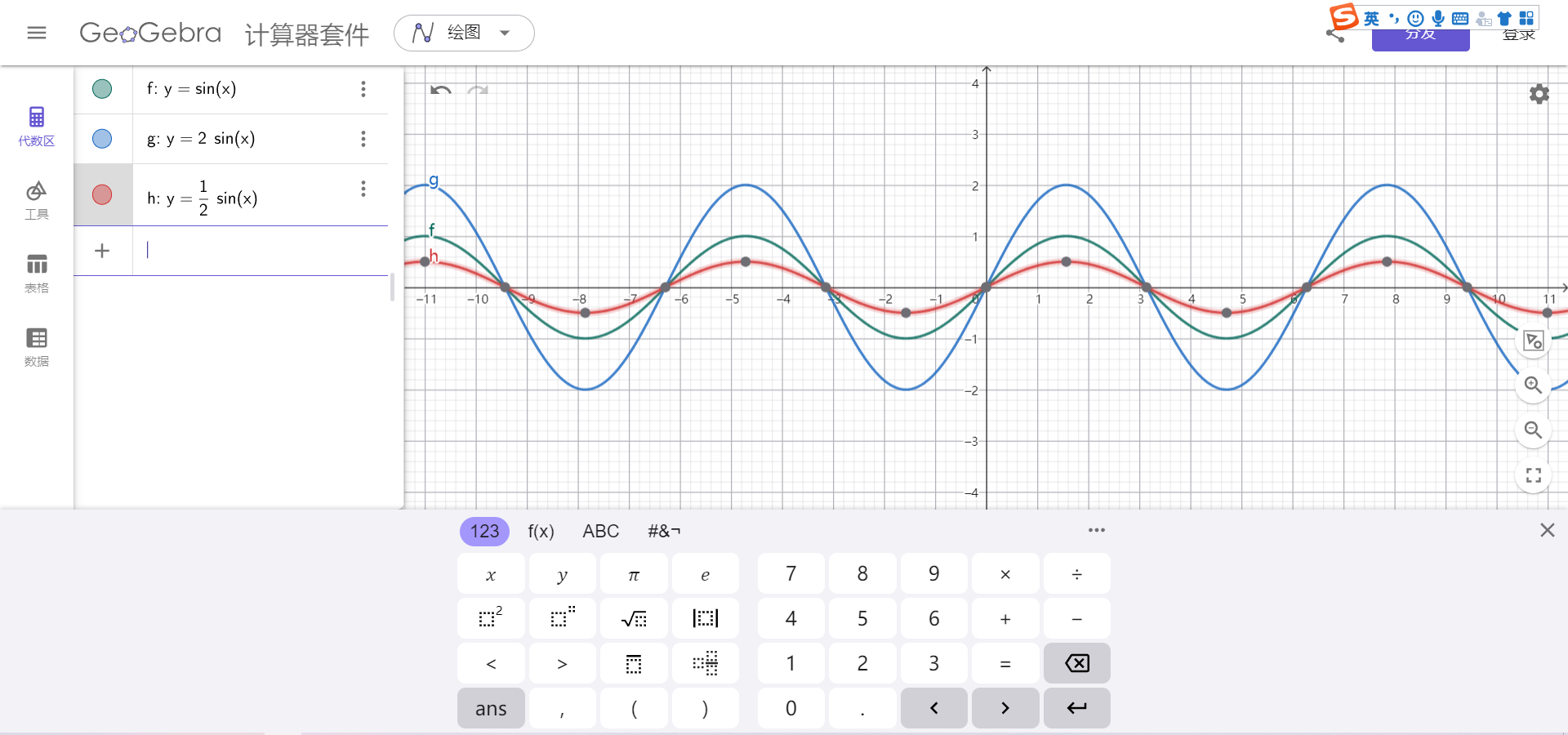
音长与振幅:
音长即声音持续时间的长度。音长也与振幅有关,声音的消失过程是由于声波在传播的过程当中受阻尼振动,系统的机械能随时间逐渐减少,振动的振幅也较小,所以振幅的变化趋势会影响声音的音长大小。
音调与频率:
音调与声音的振动频率即w有关,频率低的音调低即声音低沉,频率高的音调高即声音尖利
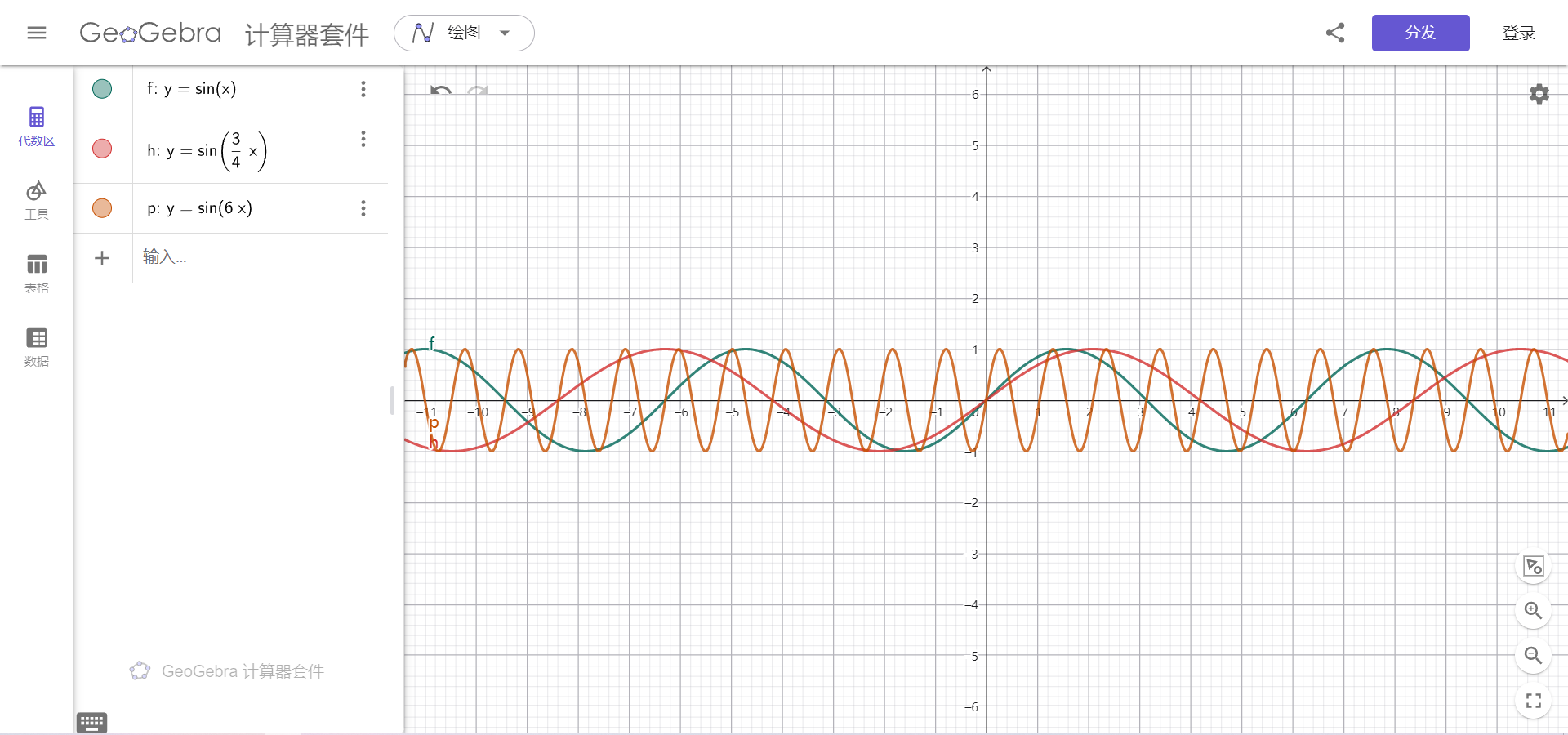
真实的声音:
在我们日常生活当中,音乐不只是一个音在响,它是许多个音的结合,称为复合音。复合音的产生是因为发声体在全段振动,产生频率为f的基音的同时,其各部分,如二分之一,三分之一,四分之一部分也在振动,产生的频率恰好是全段振动频率的倍数,如2f,3f,4f等,这些音叫谐音。因为其振幅较小,我们一般不易单独听出来,所以我们听到的声音的函数类似于:
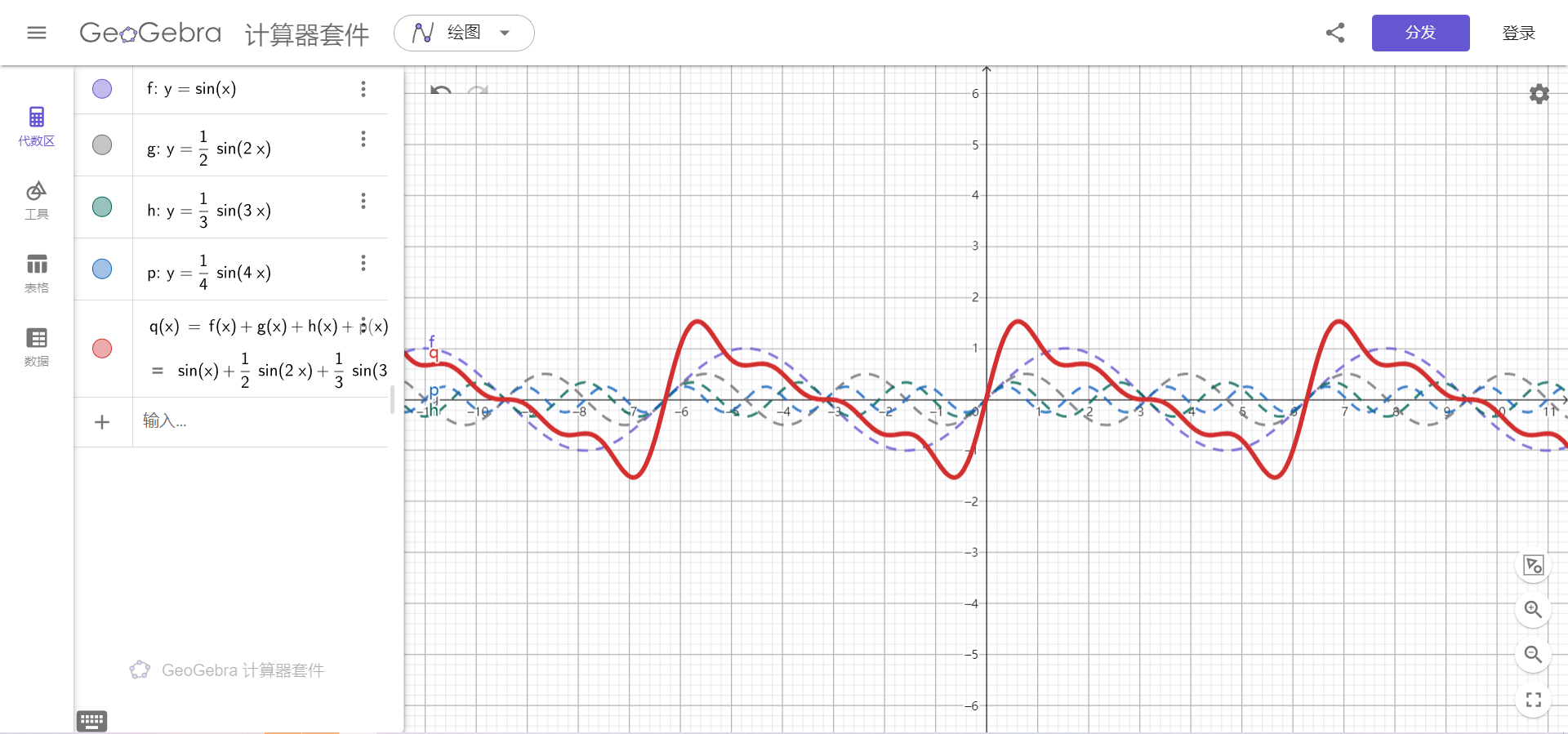
如上图f(x),g(x),h(x),p(x)为各部分音,q(x)是复合音。
傅里叶变换与复合音:
变换:
变换就是......
从向量理解:
例子。。。。
傅里叶级数:
傅里叶级数即。。。。。
傅里叶变换:
傅里叶变换就是......
欧拉公式及其改善(结合时间和角速度):
欧拉公式即。。。。利用三维
几何直观理解:
动态圆。
数学表达式(积分):
其公式是。。。
公式中各个参数变化的理解:
Dirac Delta(狄拉克δ函数):
该函数与傅里叶的数学积分表达式关系极大。
快速傅里叶变换(FFT):
快速傅里叶变化(FFT)即......(拓展内容不一定要细写)
以上探索知识的运用:
如何实现把一个人的声音换成另一个人如:。。。。
收集音频:
。。。。
傅里叶变换:
。。。。
加工其参数:
。。。。
傅里叶逆变换:
。。。。