机器人强化学习入门笔记（五）

《Walk These Ways》论文方法详解：基于行为多样性的机器人控制泛化

1. 方法总体框架

论文提出了一种称为"行为多样性"(Multiplicity of Behavior, MoB)的方法，其核心思想是训练单个策略，使其能够根据行为参数执行多种不同的运动风格。这种方法允许在不重新训练的情况下，通过调整行为参数来适应新的任务和环境。

1.1 问题背景与动机

• 传统强化学习策略通常只学习一种解决训练任务的方式，缺乏灵活适应新环境的能力
• 当遇到分布外环境时，通常需要重新设计奖励函数、环境参数并重新训练，这是一个繁琐的迭代过程
• 作者观察到：同一任务有多种等效的解决方案 ，不同解决方案在不同环境中可能有不同的泛化能力
  • 例如：在平地上行走时，"蹲伏"步态(低身体高度)和"踏步"步态(高腿摆动)都能完成任务
  • 但"蹲伏"步态能在障碍物下通过，而"踏步"步态能爬楼梯

1.2 方法形式化

作者训练了一个条件策略：
π(at∣ot−H...ot,ct−H...ct,bt−H...bt)\pi(a_t|o_{t-H}...o_t, c_{t-H}...c_t, b_{t-H}...b_t)π(at∣ot−H...ot,ct−H...ct,bt−H...bt)

其中：

• oto_tot：历史观察（关节位置/速度、重力向量等）
• ctc_tct：任务命令（期望的线速度和角速度）
• btb_tbt：行为参数（指定运动风格）
• ata_tat：动作（关节目标位置）

---

2. Go1机器人系统架构

2.1 Go1机器人本体

Unitree Go1是一款四足机器人，具有以下特点：

• 自由度配置：12个驱动关节（每条腿3个关节：髋关节、大腿关节、小腿关节）

• 关节命名 ：FL_hip_joint, FL_thigh_joint, FL_calf_joint（左前腿），FR_hip_joint, FR_thigh_joint, FR_calf_joint（右前腿），RL_hip_joint, RL_thigh_joint, RL_calf_joint（左后腿），RR_hip_joint, RR_thigh_joint, RR_calf_joint（右后腿）

• 默认关节角度（代码中定义）：

_.default_joint_angles = {  # = target angles [rad] when action = 0.0
    'FL_hip_joint': 0.1,  # [rad]
    'RL_hip_joint': 0.1,  # [rad]
    'FR_hip_joint': -0.1,  # [rad]
    'RR_hip_joint': -0.1,  # [rad]

    'FL_thigh_joint': 0.8,  # [rad]
    'RL_thigh_joint': 1.,  # [rad]
    'FR_thigh_joint': 0.8,  # [rad]
    'RR_thigh_joint': 1.,  # [rad]

    'FL_calf_joint': -1.5,  # [rad]
    'RL_calf_joint': -1.5,  # [rad]
    'FR_calf_joint': -1.5,  # [rad]
    'RR_calf_joint': -1.5  # [rad]
}

• 初始位置：躯干高度0.34m（相对于地面）

2.2 仿真环境设置

系统使用Isaac Gym作为物理仿真器：

• 并行环境数量 ：默认4000个并行环境（num_envs = 4000）
• 控制频率 ：50Hz（控制周期dt=0.02dt = 0.02dt=0.02秒）
• 仿真频率 ：更高频率的物理步进（通过decimation=4参数控制，即每4个仿真步执行一次控制更新）

环境配置（代码实现）：

_ = Cnfg.control
_.control_type = 'P'
_.stiffness = {'joint': 20.}  # [N*m/rad]
_.damping = {'joint': 0.5}  # [N*m*s/rad]
# action scale: target angle = actionScale * action + defaultAngle
_.action_scale = 0.25
_.hip_scale_reduction = 0.5
# decimation: Number of control action updates @ sim DT per policy DT
_.decimation = 4

2.3 地形生成

训练时主要使用平坦地形，但系统支持多种地形类型：

• 平坦地形：用于基础训练和sim-to-real迁移
• 地形类型 （代码支持）**：
  • 斜坡地形（sloped terrain）
  • 台阶地形（stairs）
  • 离散障碍物（discrete obstacles）
  • 随机均匀地形（random uniform terrain）

地形配置（训练时）：

_ = Cnfg.terrain
_.mesh_type = 'trimesh'
_.measure_heights = False
_.terrain_noise_magnitude = 0.0
_.teleport_robots = True
_.border_size = 50

_.terrain_proportions = [0, 0, 0, 0, 0, 0, 0, 0, 1.0]
_.curriculum = False

其中terrain_proportions的最后一个元素为1.0表示100%使用平坦地形。

---

3. 状态、观测、动作与奖励定义

3.1 状态空间（State Space）

机器人的完整状态包括：

1. 根状态（Root State）：13维向量

   • 位置：pbase∈R3p_{base} \in \mathbb{R}^3pbase∈R3（世界坐标系）
   • 四元数：qbase∈R4q_{base} \in \mathbb{R}^4qbase∈R4（姿态）
   • 线速度：vbase∈R3v_{base} \in \mathbb{R}^3vbase∈R3（世界坐标系）
   • 角速度：ωbase∈R3\omega_{base} \in \mathbb{R}^3ωbase∈R3（世界坐标系）

2. 关节状态：

   • 关节位置：q∈R12q \in \mathbb{R}^{12}q∈R12（12个关节角度）
   • 关节速度：q˙∈R12\dot{q} \in \mathbb{R}^{12}q˙∈R12（12个关节角速度）

3. 接触状态：

   • 脚部接触力：ffoot∈R4×3f_{foot} \in \mathbb{R}^{4 \times 3}ffoot∈R4×3（4只脚，每只脚3维力向量）

3.2 观测空间（Observation Space）

观测向量oto_tot由以下部分组成（按代码实现顺序）：

3.2.1 基础观测

1. 投影重力向量 （3维）：
   gproj=Rbase−1⋅gworldg_{proj} = R_{base}^{-1} \cdot g_{world}gproj=Rbase−1⋅gworld

   其中RbaseR_{base}Rbase是机器人基座旋转矩阵，gworld=[0,0,−9.81]Tg_{world} = [0, 0, -9.81]^Tgworld=[0,0,−9.81]T。投影重力向量表示机器人相对于重力的倾斜程度。

2. 任务命令 （15维，由num_commands配置）：
   ct=[vxcmd,vycmd,ωzcmd,hzcmd,fcmd,θ1cmd,θ2cmd,θ3cmd,hzf,cmd,ϕcmd,sycmd,...]c_t = [v^{cmd}_x, v^{cmd}_y, \omega^{cmd}_z, h^{cmd}_z, f^{cmd}, \theta^{cmd}_1, \theta^{cmd}_2, \theta^{cmd}_3, h^{f,cmd}_z, \phi^{cmd}, s^{cmd}_y, ...]ct=[vxcmd,vycmd,ωzcmd,hzcmd,fcmd,θ1cmd,θ2cmd,θ3cmd,hzf,cmd,ϕcmd,sycmd,...]

   包括速度命令、身体高度、步频、相位偏移、脚摆动高度、俯仰角、站立宽度等。

3. 关节位置偏差 （12维）：
   (q−qdefault)×scalepos(q - q_{default}) \times scale_{pos}(q−qdefault)×scalepos

   相对于默认关节角度的偏差，经过缩放。

4. 关节速度 （12维）：
   q˙×scalevel\dot{q} \times scale_{vel}q˙×scalevel

   关节角速度，经过缩放。

5. 上一时刻动作 （12维）：

   用于动作平滑性。

代码实现：

def compute_observations(self):
    """ Computes observations
    """
    self.obs_buf = torch.cat((self.projected_gravity,
                              (self.dof_pos[:, :self.num_actuated_dof] - self.default_dof_pos[:,
                                                                         :self.num_actuated_dof]) * self.obs_scales.dof_pos,
                              self.dof_vel[:, :self.num_actuated_dof] * self.obs_scales.dof_vel,
                              self.actions
                              ), dim=-1)

    if self.cfg.env.observe_command:
        self.obs_buf = torch.cat((self.projected_gravity,
                                  self.commands * self.commands_scale,
                                  (self.dof_pos[:, :self.num_actuated_dof] - self.default_dof_pos[:,
                                                                                 :self.num_actuated_dof]) * self.obs_scales.dof_pos,
                                  self.dof_vel[:, :self.num_actuated_dof] * self.obs_scales.dof_vel,
                                  self.actions
                                  ), dim=-1)

    if self.cfg.env.observe_two_prev_actions:
        self.obs_buf = torch.cat((self.obs_buf,
                                  self.last_actions), dim=-1)

3.2.2 可选观测

根据配置，可能还包括：

• 时钟输入 （4维）：每个脚的正弦定时变量
  clockfoot=sin⁡(2π⋅tfoot)clock_{foot} = \sin(2\pi \cdot t_{foot})clockfoot=sin(2π⋅tfoot)

• 速度观测（6维）：基座线速度和角速度（本体坐标系）

• 接触状态（4维）：每只脚是否接触地面

时钟输入计算（代码实现）：

if self.cfg.env.observe_clock_inputs:
    self.obs_buf = torch.cat((self.obs_buf,
                              self.clock_inputs), dim=-1)

3.2.3 历史观测

系统使用30步历史观测 （num_observation_history = 30），通过HistoryWrapper实现：

self.obs_history_length = self.env.cfg.env.num_observation_history

self.num_obs_history = self.obs_history_length * self.num_obs
self.obs_history = torch.zeros(self.env.num_envs, self.num_obs_history, dtype=torch.float,
                               device=self.env.device, requires_grad=False)

最终输入到策略网络的观测维度为：30×70=210030 \times 70 = 210030×70=2100维（假设单步观测为70维）。

3.3 动作空间（Action Space）

动作at∈R12a_t \in \mathbb{R}^{12}at∈R12表示12个关节的目标位置偏移。

动作到目标关节角度的转换 ：
qtarget=at×scaleaction×scalehip+qdefaultq_{target} = a_t \times scale_{action} \times scale_{hip} + q_{default}qtarget=at×scaleaction×scalehip+qdefault

其中：

• scaleaction=0.25scale_{action} = 0.25scaleaction=0.25：全局动作缩放
• scalehip=0.5scale_{hip} = 0.5scalehip=0.5：髋关节额外缩放（减小髋关节运动范围）
• qdefaultq_{default}qdefault：默认关节角度

代码实现：

# pd controller
actions_scaled = actions[:, :12] * self.cfg.control.action_scale
actions_scaled[:, [0, 3, 6, 9]] *= self.cfg.control.hip_scale_reduction  # scale down hip flexion range

if self.cfg.domain_rand.randomize_lag_timesteps:
    self.lag_buffer = self.lag_buffer[1:] + [actions_scaled.clone()]
    self.joint_pos_target = self.lag_buffer[0] + self.default_dof_pos
else:
    self.joint_pos_target = actions_scaled + self.default_dof_pos

3.4 从动作到电机扭矩的完整流程

3.4.1 PD控制器

系统使用PD（比例-微分）控制器将目标关节位置转换为关节扭矩：

τ=Kp⋅Kp,factor⋅(qtarget−q+Δqoffset)−Kd⋅Kd,factor⋅q˙\tau = K_p \cdot K_{p,factor} \cdot (q_{target} - q + \Delta q_{offset}) - K_d \cdot K_{d,factor} \cdot \dot{q}τ=Kp⋅Kp,factor⋅(qtarget−q+Δqoffset)−Kd⋅Kd,factor⋅q˙

其中：

• Kp=20K_p = 20Kp=20 N·m/rad：比例增益（刚度）
• Kd=0.5K_d = 0.5Kd=0.5 N·m·s/rad：微分增益（阻尼）
• Kp,factor,Kd,factorK_{p,factor}, K_{d,factor}Kp,factor,Kd,factor：域随机化的增益因子
• Δqoffset\Delta q_{offset}Δqoffset：电机位置偏移（域随机化）

代码实现：

elif control_type == "P":
    torques = self.p_gains * self.Kp_factors * (
            self.joint_pos_target - self.dof_pos + self.motor_offsets) - self.d_gains * self.Kd_factors * self.dof_vel

3.4.2 执行器网络（Actuator Network）

为了更准确地模拟真实电机行为，系统使用执行器网络替代理想PD控制器。执行器网络是一个神经网络，输入为：

x=[et,et−1,et−2,q˙t,q˙t−1,q˙t−2]x = [e_t, e_{t-1}, e_{t-2}, \dot{q}t, \dot{q}{t-1}, \dot{q}_{t-2}]x=[et,et−1,et−2,q˙t,q˙t−1,q˙t−2]

其中et=qtarget−qe_t = q_{target} - qet=qtarget−q是位置误差。

代码实现：

if control_type == "actuator_net":
    self.joint_pos_err = self.dof_pos - self.joint_pos_target + self.motor_offsets
    self.joint_vel = self.dof_vel
    torques = self.actuator_network(self.joint_pos_err, self.joint_pos_err_last, self.joint_pos_err_last_last,
                                    self.joint_vel, self.joint_vel_last, self.joint_vel_last_last)
    self.joint_pos_err_last_last = torch.clone(self.joint_pos_err_last)
    self.joint_pos_err_last = torch.clone(self.joint_pos_err)
    self.joint_vel_last_last = torch.clone(self.joint_vel_last)
    self.joint_vel_last = torch.clone(self.joint_vel)

执行器网络从预训练模型加载：

if self.cfg.control.control_type == "actuator_net":
    actuator_path = f'{os.path.dirname(os.path.dirname(os.path.realpath(__file__)))}/../../resources/actuator_nets/unitree_go1.pt'
    actuator_network = torch.jit.load(actuator_path).to(self.device)

3.4.3 扭矩限制

最终扭矩经过限制和电机强度缩放：

τfinal=clip(τ×strengthmotor,−τlimit,τlimit)\tau_{final} = clip(\tau \times strength_{motor}, -\tau_{limit}, \tau_{limit})τfinal=clip(τ×strengthmotor,−τlimit,τlimit)

代码实现：

torques = torques * self.motor_strengths
return torch.clip(torques, -self.torque_limits, self.torque_limits)

3.4.4 完整控制流程总结

从速度/位置指令到电机扭矩的完整流程：

1. 策略网络输出 ：at∈R12a_t \in \mathbb{R}^{12}at∈R12（动作）
2. 动作缩放 ：ascaled=at×0.25a_{scaled} = a_t \times 0.25ascaled=at×0.25，髋关节额外缩放×0.5\times 0.5×0.5
3. 目标关节角度 ：qtarget=ascaled+qdefaultq_{target} = a_{scaled} + q_{default}qtarget=ascaled+qdefault
4. PD控制/执行器网络 ：
   • PD模式：τ=Kp(qtarget−q)−Kdq˙\tau = K_p(q_{target} - q) - K_d \dot{q}τ=Kp(qtarget−q)−Kdq˙
   • 执行器网络模式：τ=ActuatorNet(et,et−1,et−2,q˙t,q˙t−1,q˙t−2)\tau = ActuatorNet(e_t, e_{t-1}, e_{t-2}, \dot{q}t, \dot{q}{t-1}, \dot{q}_{t-2})τ=ActuatorNet(et,et−1,et−2,q˙t,q˙t−1,q˙t−2)
5. 扭矩限制 ：τfinal=clip(τ×strength,−τmax,τmax)\tau_{final} = clip(\tau \times strength, -\tau_{max}, \tau_{max})τfinal=clip(τ×strength,−τmax,τmax)
6. 发送到仿真器 ：τfinal\tau_{final}τfinal直接作用于关节

---

4. 任务与行为参数设计

4.1 任务命令 (Task Specification)

任务指定为3维命令向量：
ct=[vxcmd,vycmd,ωzcmd]c_t = [v^{cmd}_x, v^{cmd}_y, \omega^{cmd}_z]ct=[vxcmd,vycmd,ωzcmd]

• vxcmd,vycmdv^{cmd}_x, v^{cmd}_yvxcmd,vycmd：在机器人本体坐标系x-y轴上期望的线速度
• ωzcmd\omega^{cmd}_zωzcmd：在偏航轴(yaw axis)上期望的角速度

采样范围（代码配置）：

_ = Cnfg.commands
_.heading_command = False
_.resampling_time = 10.0
_.command_curriculum = True
_.num_lin_vel_bins = 30
_.num_ang_vel_bins = 30
_.lin_vel_x = [-0.6, 0.6]
_.lin_vel_y = [-0.6, 0.6]
_.ang_vel_yaw = [-1, 1]

4.2 行为参数 (Behavior Specification)

行为参数定义为15维向量（代码中num_commands = 15）。完整定义如下：

bt=[vxcmd,vycmd,ωzcmd,hzcmd,fcmd,θ1cmd,θ2cmd,θ3cmd,dcmd,hzf,cmd,ϕcmd,ψcmd,sycmd,lcmd,...]b_t = [v^{cmd}_x, v^{cmd}_y, \omega^{cmd}_z, h^{cmd}_z, f^{cmd}, \theta^{cmd}_1, \theta^{cmd}_2, \theta^{cmd}_3, d^{cmd}, h^{f,cmd}_z, \phi^{cmd}, \psi^{cmd}, s^{cmd}_y, l^{cmd}, ...]bt=[vxcmd,vycmd,ωzcmd,hzcmd,fcmd,θ1cmd,θ2cmd,θ3cmd,dcmd,hzf,cmd,ϕcmd,ψcmd,sycmd,lcmd,...]

完整参数列表：

索引	符号	名称	采样范围	用途说明
0	vxcmdv^{cmd}_xvxcmd	线速度x命令	[-1.0, 1.0] m/s	任务命令，用于速度跟踪奖励
1	vycmdv^{cmd}_yvycmd	线速度y命令	[-0.6, 0.6] m/s	任务命令，用于速度跟踪奖励
2	ωzcmd\omega^{cmd}_zωzcmd	角速度yaw命令	[-1.0, 1.0] rad/s	任务命令，用于角速度跟踪奖励和Raibert启发式
3	hzcmdh^{cmd}_zhzcmd	身体高度命令	[-0.25, 0.15] m	去掉基座高度的净身高，用于身体高度跟踪奖励（_reward_jump）
4	fcmdf^{cmd}fcmd	步频命令	[2.0, 4.0] Hz	用于计算步态相位和Raibert启发式
5	θ1cmd\theta^{cmd}_1θ1cmd (phases)	相位偏移1	[0.0, 1.0]	用于计算步态相位偏移，影响期望接触状态和时钟输入
6	θ2cmd\theta^{cmd}_2θ2cmd (offsets)	相位偏移2	[0.0, 1.0]	用于计算步态相位偏移，影响期望接触状态和时钟输入
7	θ3cmd\theta^{cmd}_3θ3cmd (bounds)	相位偏移3	[0.0, 1.0]	用于计算步态相位偏移，影响期望接触状态和时钟输入
8	dcmdd^{cmd}dcmd (durations)	支撑相持续时间	[0.5, 0.5]	用于durations warping，影响期望接触状态计算
9	hzf,cmdh^{f,cmd}_zhzf,cmd	脚摆动高度命令	[0.03, 0.35] m	用于脚摆动高度跟踪奖励（_reward_feet_clearance_cmd_linear）
10	ϕcmd\phi^{cmd}ϕcmd (body_pitch)	身体俯仰角命令	[-0.4, 0.4] rad	用于身体姿态控制奖励（_reward_orientation_control）
11	ψcmd\psi^{cmd}ψcmd (body_roll)	身体滚动角命令	[-0.0, 0.0] rad	用于身体姿态控制奖励（_reward_orientation_control）
12	sycmds^{cmd}_ysycmd (stance_width)	站立宽度命令	[0.10, 0.45] m	用于Raibert启发式奖励，计算期望脚位置
13	lcmdl^{cmd}lcmd (stance_length)	站立长度命令	[0.35, 0.45] m	用于Raibert启发式奖励，计算期望脚位置
14	-	(预留)	-	当前未使用

参数使用位置总结：

• 任务命令（索引0-2）：用于任务奖励（速度跟踪）
• 步态参数（索引4-8）：用于计算期望接触状态、时钟输入、步态相位
• 身体参数（索引3, 10-11）：用于身体高度和姿态跟踪奖励
• 脚部参数（索引9, 12-13）：用于脚摆动高度和Raibert启发式奖励

4.2.1 步态相位偏移 (Timing Offsets)

用"相位（phase）"来描述一条腿在一个步态周期中的时间位置；用"相位偏移（offset）"来让四条腿在同一个周期里"错开"，从而形成小跑/踱步/跳跃等典型步态。

4.2.1.1 步态基础概念

什么是步态？ 步态（Gait）是指四足动物行走时，四条腿的协调运动模式。每条腿的运动可以分为两个阶段：

• 支撑相（Stance Phase）：脚接触地面，支撑身体
• 摆动相（Swing Phase）：脚离开地面，向前摆动

什么是相位？ 相位（Phase）表示每条腿在步态周期中的位置。我们将一个完整的步态周期归一化为0到1之间的数值：

• 相位 = 0：步态周期开始
• 相位 = 0.5：步态周期的一半
• 相位 = 1：步态周期结束（等同于0，因为周期是循环的）

相位偏移的作用：通过调整不同腿之间的相位差，可以产生不同的步态模式。例如：

• 如果两条腿的相位差为0，它们会同时抬起和放下（同步）
• 如果两条腿的相位差为0.5，它们会交替抬起和放下（异步）

4.2.1.2 四足机器人的腿编号

Go1机器人有四条腿，按以下方式编号：

• FL（Front Left）：左前腿
• FR（Front Right）：右前腿
• RL（Rear Left）：左后腿
• RR（Rear Right）：右后腿

从上方俯视机器人：

    FL  |  FR
    ----|----
    RL  |  RR

4.2.1.3 步态相位偏移参数

系统使用三个参数来控制四条腿之间的相位关系：
θcmd=(θ1cmd,θ2cmd,θ3cmd)\theta^{cmd} = (\theta^{cmd}_1, \theta^{cmd}_2, \theta^{cmd}_3)θcmd=(θ1cmd,θ2cmd,θ3cmd)

这些参数分别对应代码中的：

• phases = θ1cmd\theta^{cmd}_1θ1cmd：主要相位偏移
• offsets = θ2cmd\theta^{cmd}_2θ2cmd：次要偏移
• bounds = θ3cmd\theta^{cmd}_3θ3cmd：边界偏移

核心思想：通过给每条腿的相位加上不同的偏移量，可以控制哪些腿同步运动，哪些腿交替运动。

4.2.1.4 步态索引的计算

系统维护一个全局的步态索引tgaitt_{gait}tgait，它从0开始，随着时间递增到1，然后循环：

tgait=remainder(tgait+dt×fcmd,1.0)t_{gait} = \text{remainder}(t_{gait} + dt \times f^{cmd}, 1.0)tgait=remainder(tgait+dt×fcmd,1.0)

其中：

• dt=0.02dt = 0.02dt=0.02秒：控制周期
• fcmdf^{cmd}fcmd：步频（Hz），表示每秒完成多少个步态周期
• 例如：fcmd=3f^{cmd} = 3fcmd=3 Hz表示每秒3个周期，每个周期约0.33秒

每条腿的相位计算（代码实现）：

def _step_contact_targets(self):
    if self.cfg.env.observe_gait_commands:
        frequencies = self.commands[:, 4]
        phases = self.commands[:, 5]
        offsets = self.commands[:, 6]
        bounds = self.commands[:, 7]
        durations = self.commands[:, 8]
        self.gait_indices = torch.remainder(self.gait_indices + self.dt * frequencies, 1.0)

        if self.cfg.commands.pacing_offset:
            foot_indices = [self.gait_indices + phases + offsets + bounds,
                            self.gait_indices + bounds,
                            self.gait_indices + offsets,
                            self.gait_indices + phases]
        else:
            foot_indices = [self.gait_indices + phases + offsets + bounds,
                            self.gait_indices + offsets,
                            self.gait_indices + bounds,
                            self.gait_indices + phases]

        self.foot_indices = torch.remainder(torch.cat([foot_indices[i].unsqueeze(1) for i in range(4)], dim=1), 1.0)

在默认配置下（pacing_offset = False），每条腿的相位计算为：

• FL（左前） ：tFL=tgait+θ1+θ2+θ3t_{FL} = t_{gait} + \theta_1 + \theta_2 + \theta_3tFL=tgait+θ1+θ2+θ3
• FR（右前） ：tFR=tgait+θ2t_{FR} = t_{gait} + \theta_2tFR=tgait+θ2
• RL（左后） ：tRL=tgait+θ3t_{RL} = t_{gait} + \theta_3tRL=tgait+θ3
• RR（右后） ：tRR=tgait+θ1t_{RR} = t_{gait} + \theta_1tRR=tgait+θ1

关键理解：每条腿的相位 = 基础相位 + 偏移量。如果两条腿的偏移量相同，它们的相位就相同，会同步运动；如果偏移量相差0.5，它们会交替运动。

4.2.1.5 典型步态配置详解

让我们通过具体例子理解为什么不同的参数设置会产生不同的步态：

1. 小跑（Trotting）步态：θcmd=(0.5,0,0)\theta^{cmd} = (0.5, 0, 0)θcmd=(0.5,0,0)

计算每条腿的相位：

• FL：tFL=tgait+0.5+0+0=tgait+0.5t_{FL} = t_{gait} + 0.5 + 0 + 0 = t_{gait} + 0.5tFL=tgait+0.5+0+0=tgait+0.5
• FR：tFR=tgait+0+0=tgaitt_{FR} = t_{gait} + 0 + 0 = t_{gait}tFR=tgait+0+0=tgait
• RL：tRL=tgait+0=tgaitt_{RL} = t_{gait} + 0 = t_{gait}tRL=tgait+0=tgait
• RR：tRR=tgait+0.5t_{RR} = t_{gait} + 0.5tRR=tgait+0.5

结果：

• FR和RL的相位相同（都是tgaitt_{gait}tgait），它们同步运动
• FL和RR的相位相同（都是tgait+0.5t_{gait} + 0.5tgait+0.5），它们同步运动
• 前一对（FR+RL）和后一对（FL+RR）的相位相差0.5，它们交替运动

视觉化（用"●"表示脚在地面，"○"表示脚抬起）：

时间点1:   FL○ FR●
          RL●  RR○
          
时间点2:  FL● FR○ 
         RL○  RR●

这就是对角线脚对同步的小跑步态，像马一样奔跑。

2. 跳跃（Pronking）步态：θcmd=(0.0,0,0)\theta^{cmd} = (0.0, 0, 0)θcmd=(0.0,0,0)

计算每条腿的相位：

• FL：tFL=tgait+0+0+0=tgaitt_{FL} = t_{gait} + 0 + 0 + 0 = t_{gait}tFL=tgait+0+0+0=tgait
• FR：tFR=tgait+0=tgaitt_{FR} = t_{gait} + 0 = t_{gait}tFR=tgait+0=tgait
• RL：tRL=tgait+0=tgaitt_{RL} = t_{gait} + 0 = t_{gait}tRL=tgait+0=tgait
• RR：tRR=tgait+0=tgaitt_{RR} = t_{gait} + 0 = t_{gait}tRR=tgait+0=tgait

结果 ：所有腿的相位都相同，它们同时抬起和放下，就像兔子跳跃一样。

视觉化：

时间点1:    FL● FR●
            RR● RL●
          
时间点2:    FL○ FR○
            RR○ RL○

3. 跳跃（Bounding）步态：θcmd=(0,0.5,0)\theta^{cmd} = (0, 0.5, 0)θcmd=(0,0.5,0)

计算每条腿的相位：

• FL：tFL=tgait+0+0.5+0=tgait+0.5t_{FL} = t_{gait} + 0 + 0.5 + 0 = t_{gait} + 0.5tFL=tgait+0+0.5+0=tgait+0.5
• FR：tFR=tgait+0.5=tgait+0.5t_{FR} = t_{gait} + 0.5 = t_{gait} + 0.5tFR=tgait+0.5=tgait+0.5
• RL：tRL=tgait+0=tgaitt_{RL} = t_{gait} + 0 = t_{gait}tRL=tgait+0=tgait
• RR：tRR=tgait+0=tgaitt_{RR} = t_{gait} + 0 = t_{gait}tRR=tgait+0=tgait

结果：

• 前腿（FL+FR）的相位相同，它们同步运动
• 后腿（RL+RR）的相位相同，它们同步运动
• 前腿和后腿的相位相差0.5，它们交替运动

视觉化：

时间点1:   FL● FR● 
          RL○  RR○
          
时间点2:   FL○ FR○ 
          RL●  RR●

这就是前后脚对同步的跳跃步态，像狗一样跳跃前进。

4. 踱步（Pacing）步态：θcmd=(0,0,0.5)\theta^{cmd} = (0, 0, 0.5)θcmd=(0,0,0.5)

计算每条腿的相位：

• FL：tFL=tgait+0+0+0.5=tgait+0.5t_{FL} = t_{gait} + 0 + 0 + 0.5 = t_{gait} + 0.5tFL=tgait+0+0+0.5=tgait+0.5
• FR：tFR=tgait+0=tgaitt_{FR} = t_{gait} + 0 = t_{gait}tFR=tgait+0=tgait
• RL：tRL=tgait+0.5=tgait+0.5t_{RL} = t_{gait} + 0.5 = t_{gait} + 0.5tRL=tgait+0.5=tgait+0.5
• RR：tRR=tgait+0=tgaitt_{RR} = t_{gait} + 0 = t_{gait}tRR=tgait+0=tgait

结果：

• 左侧腿（FL+RL）的相位相同，它们同步运动
• 右侧腿（FR+RR）的相位相同，它们同步运动
• 左侧和右侧的相位相差0.5，它们交替运动

视觉化：

时间点1:    FL○ FR●
          RL○  RR●
          
时间点2:    FL● FR○
          RL●  RR○

这就是左右侧脚对同步的踱步步态，像骆驼一样行走。

4.2.1.6 支撑相持续时间

durations参数控制每条腿在支撑相（脚接触地面）的时间比例，通常设置为0.5，表示：

• 50%的时间脚在地面（支撑相）
• 50%的时间脚在空中（摆动相）

这个参数对所有腿都相同，确保步态的对称性。

4.2.2 期望接触状态计算

4.2.2.1 什么是期望接触状态？

期望接触状态 CfootcmdC^{cmd}_{foot}Cfootcmd是一个0到1之间的数值，表示在某个时刻，某条腿应该接触地面的概率：

• Cfootcmd=1C^{cmd}_{foot} = 1Cfootcmd=1：这条腿应该完全接触地面（支撑相）
• Cfootcmd=0C^{cmd}_{foot} = 0Cfootcmd=0：这条腿应该完全离开地面（摆动相）
• Cfootcmd=0.5C^{cmd}_{foot} = 0.5Cfootcmd=0.5：处于过渡状态

为什么需要期望接触状态？ 在强化学习中，我们需要告诉策略"在某个时刻，某条腿应该接触地面"。这样策略才能学习正确的步态模式。

4.2.2.2 理想情况 vs 实际情况

理想情况：如果我们简单地定义：

• 当tfoot<0.5t_{foot} < 0.5tfoot<0.5时，Cfootcmd=1C^{cmd}_{foot} = 1Cfootcmd=1（支撑相）
• 当tfoot≥0.5t_{foot} \geq 0.5tfoot≥0.5时，Cfootcmd=0C^{cmd}_{foot} = 0Cfootcmd=0（摆动相）

这会产生一个硬切换 （硬边界），在tfoot=0.5t_{foot} = 0.5tfoot=0.5处突然从1跳到0。

问题：硬切换会导致：

1. 训练不稳定：策略难以学习在切换点附近的行为
2. 奖励信号不连续：在切换点附近，奖励函数会突然变化
3. 实际运动不自然：真实世界中，脚的接触是逐渐发生的

4.2.2.3 平滑过渡的必要性

解决方案 ：使用平滑函数 来定义期望接触状态，让它在支撑相和摆动相之间平滑过渡。

系统使用**正态分布的累积密度函数（CDF）**来实现平滑过渡。CDF函数的特点是：

• 输入值很小时，输出接近0
• 输入值很大时，输出接近1
• 在中间区域，输出平滑地从0过渡到1

4.2.2.4 期望接触状态的计算公式

数学表达 ：
Cfootcmd(tfoot)=Φ(tfoot;κ)×(1−Φ(tfoot−0.5;κ))+Φ(tfoot−1;κ)×(1−Φ(tfoot−1.5;κ))C^{cmd}{foot}(t{foot}) = \Phi(t_{foot}; \kappa) \times (1-\Phi(t_{foot}-0.5; \kappa)) + \Phi(t_{foot}-1; \kappa) \times (1-\Phi(t_{foot}-1.5; \kappa))Cfootcmd(tfoot)=Φ(tfoot;κ)×(1−Φ(tfoot−0.5;κ))+Φ(tfoot−1;κ)×(1−Φ(tfoot−1.5;κ))

其中Φ(x;κ)\Phi(x; \kappa)Φ(x;κ)是均值为0、标准差为κ\kappaκ的正态分布CDF。κ=0.07\kappa = 0.07κ=0.07（kappa_gait_probs）控制接触-摆动转换的平滑度。

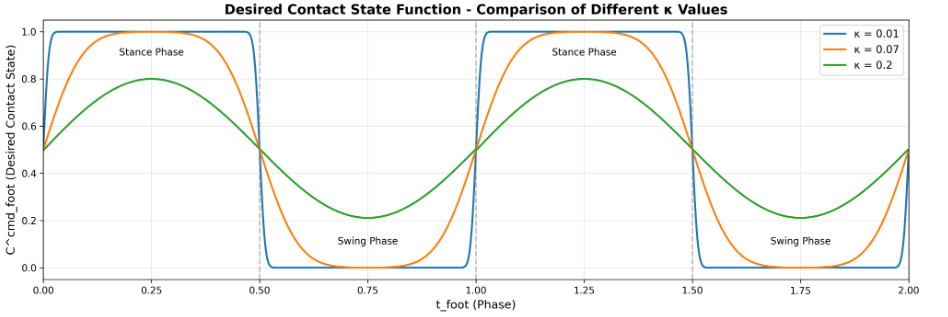
公式解释：

这个公式看起来复杂，但实际上它做了两件事：

1. 第一个周期 （0≤tfoot<10 \leq t_{foot} < 10≤tfoot<1）：

   • 当tfoott_{foot}tfoot从0增加到0.5时，Φ(tfoot)\Phi(t_{foot})Φ(tfoot)从0增加到接近1，所以CfootcmdC^{cmd}_{foot}Cfootcmd从0增加到接近1（进入支撑相）
   • 当tfoott_{foot}tfoot从0.5增加到1时，Φ(tfoot−0.5)\Phi(t_{foot}-0.5)Φ(tfoot−0.5)从0增加到接近1，所以(1−Φ(tfoot−0.5))(1-\Phi(t_{foot}-0.5))(1−Φ(tfoot−0.5))从1减少到接近0，导致CfootcmdC^{cmd}_{foot}Cfootcmd从1减少到接近0（进入摆动相）

2. 第二个周期 （1≤tfoot<21 \leq t_{foot} < 21≤tfoot<2，通过模运算tfoot−1t_{foot}-1tfoot−1映射回0-1）：

   • 处理周期边界的情况，确保连续性

直观理解：

• 当tfoot=0t_{foot} = 0tfoot=0时：Cfootcmd≈0C^{cmd}_{foot} \approx 0Cfootcmd≈0（脚刚抬起）
• 当tfoot=0.25t_{foot} = 0.25tfoot=0.25时：Cfootcmd≈0.5C^{cmd}_{foot} \approx 0.5Cfootcmd≈0.5（过渡中）
• 当tfoot=0.5t_{foot} = 0.5tfoot=0.5时：Cfootcmd≈1C^{cmd}_{foot} \approx 1Cfootcmd≈1（完全接触）
• 当tfoot=0.75t_{foot} = 0.75tfoot=0.75时：Cfootcmd≈0.5C^{cmd}_{foot} \approx 0.5Cfootcmd≈0.5（过渡中）
• 当tfoot=1t_{foot} = 1tfoot=1时：Cfootcmd≈0C^{cmd}_{foot} \approx 0Cfootcmd≈0（脚刚抬起，开始新周期）

κ\kappaκ参数的作用：

• κ\kappaκ越小（如0.01），过渡越陡峭，接近硬切换
• κ\kappaκ越大（如0.2），过渡越平缓，但可能不够明确
• κ=0.07\kappa = 0.07κ=0.07是一个平衡值，既保证了平滑性，又保持了明确的支撑/摆动区分

代码实现：

# von mises distribution
kappa = self.cfg.rewards.kappa_gait_probs
smoothing_cdf_start = torch.distributions.normal.Normal(0,
                                                        kappa).cdf  # (x) + torch.distributions.normal.Normal(1, kappa).cdf(x)) / 2

smoothing_multiplier_FL = (smoothing_cdf_start(torch.remainder(foot_indices[0], 1.0)) * (
        1 - smoothing_cdf_start(torch.remainder(foot_indices[0], 1.0) - 0.5)) +
                               smoothing_cdf_start(torch.remainder(foot_indices[0], 1.0) - 1) * (
                                       1 - smoothing_cdf_start(
                                   torch.remainder(foot_indices[0], 1.0) - 0.5 - 1)))
# ... 类似地计算其他腿的期望接触状态 ...

self.desired_contact_states[:, 0] = smoothing_multiplier_FL
self.desired_contact_states[:, 1] = smoothing_multiplier_FR
self.desired_contact_states[:, 2] = smoothing_multiplier_RL
self.desired_contact_states[:, 3] = smoothing_multiplier_RR

代码中torch.remainder(foot_indices[i], 1.0)确保相位值在0-1范围内，处理周期循环。

4.2.2.5 期望接触状态的使用

在奖励计算中的应用：

desired_contact_states主要用于计算增强辅助奖励，确保策略按照指定的步态模式执行：

1. 摆动相位跟踪奖励（力） （_reward_tracking_contacts_shaped_force）：

   def _reward_tracking_contacts_shaped_force(self):
       foot_forces = torch.norm(self.env.contact_forces[:, self.env.feet_indices, :], dim=-1)
       desired_contact = self.env.desired_contact_states
       
       reward = 0
       for i in range(4):
           reward += - (1 - desired_contact[:, i]) * (
                       1 - torch.exp(-1 * foot_forces[:, i] ** 2 / self.env.cfg.rewards.gait_force_sigma))
       return reward / 4

   当脚应该处于摆动阶段时（1−Cfootcmd=11 - C^{cmd}_{foot} = 11−Cfootcmd=1），奖励鼓励零接触力。如果摆动阶段的脚仍然接触地面，会受到惩罚。

2. 支撑相位跟踪奖励（速度） （_reward_tracking_contacts_shaped_vel）：

   def _reward_tracking_contacts_shaped_vel(self):
       foot_velocities = torch.norm(self.env.foot_velocities, dim=2).view(self.env.num_envs, -1)
       desired_contact = self.env.desired_contact_states
       reward = 0
       for i in range(4):
           reward += - (desired_contact[:, i] * (
                       1 - torch.exp(-1 * foot_velocities[:, i] ** 2 / self.env.cfg.rewards.gait_vel_sigma)))
       return reward / 4

   当脚应该处于支撑阶段时（Cfootcmd=1C^{cmd}_{foot} = 1Cfootcmd=1），奖励鼓励脚在地面上保持静止。如果支撑阶段的脚滑动，会受到惩罚。

3. 脚摆动高度跟踪奖励 （_reward_feet_clearance_cmd_linear）：

   def _reward_feet_clearance_cmd_linear(self):
       phases = 1 - torch.abs(1.0 - torch.clip((self.env.foot_indices * 2.0) - 1.0, 0.0, 1.0) * 2.0)
       foot_height = (self.env.foot_positions[:, :, 2]).view(self.env.num_envs, -1)
       target_height = self.env.commands[:, 9].unsqueeze(1) * phases + 0.02
       rew_foot_clearance = torch.square(target_height - foot_height) * (1 - self.env.desired_contact_states)
       return torch.sum(rew_foot_clearance, dim=1)

   仅在摆动阶段（1−Cfootcmd=11 - C^{cmd}_{foot} = 11−Cfootcmd=1）惩罚脚高度偏差，确保脚在摆动时达到指定高度。

4.2.3.2 时钟输入的计算

数学公式 ：
clockfoot=sin⁡(2π⋅tfoot)clock_{foot} = \sin(2\pi \cdot t_{foot})clockfoot=sin(2π⋅tfoot)

其中tfoott_{foot}tfoot是每条腿的相位（0到1之间）。

重要：durations warping处理

在计算clock_inputs之前，foot_indices还经过了durations warping处理，这是一个关键步骤：

for idxs in foot_indices:
    stance_idxs = torch.remainder(idxs, 1) < durations
    swing_idxs = torch.remainder(idxs, 1) > durations

    idxs[stance_idxs] = torch.remainder(idxs[stance_idxs], 1) * (0.5 / durations[stance_idxs])
    idxs[swing_idxs] = 0.5 + (torch.remainder(idxs[swing_idxs], 1) - durations[swing_idxs]) * (
                0.5 / (1 - durations[swing_idxs]))

durations warping的作用：

这个处理将原始的foot_indices（基于步态周期）重新映射，使得：

• 支撑相 （原始0到durations）被映射到0到0.5
• 摆动相 （原始durations到1）被映射到0.5到1

为什么需要warping？

• 当durations = 0.5时（50%支撑，50%摆动），warping是恒等映射（0→0，0.5→0.5，1→1）
• 当durations ≠ 0.5时，warping确保支撑相和摆动相在时钟输入中占据相等的"时间"（各占0.5）
• 这使得sin函数能够均匀地表示支撑相和摆动相，而不是根据实际的支撑/摆动时间比例

warping后的语义变化：

经过warping后，foot_indices的语义从"在步态周期中的位置"变成了"在支撑相或摆动相中的位置"：

• 0-0.5：在支撑相中的位置（0=支撑相开始，0.5=支撑相结束）
• 0.5-1：在摆动相中的位置（0.5=摆动相开始，1=摆动相结束）

然后sin映射将这个"支撑/摆动位置"转换为带方向的信号。

直观理解 （warping后的foot_indices经过sin映射）：

• 当tfoot=0t_{foot} = 0tfoot=0时：sin⁡(0)=0\sin(0) = 0sin(0)=0（支撑相开始）
• 当tfoot=0.25t_{foot} = 0.25tfoot=0.25时：sin⁡(π/2)=1\sin(\pi/2) = 1sin(π/2)=1（支撑相中点，最大值）
• 当tfoot=0.5t_{foot} = 0.5tfoot=0.5时：sin⁡(π)=0\sin(\pi) = 0sin(π)=0（支撑相结束/摆动相开始）
• 当tfoot=0.75t_{foot} = 0.75tfoot=0.75时：sin⁡(3π/2)=−1\sin(3\pi/2) = -1sin(3π/2)=−1（摆动相中点，最小值）
• 当tfoot=1t_{foot} = 1tfoot=1时：sin⁡(2π)=0\sin(2\pi) = 0sin(2π)=0（摆动相结束，等同于周期开始）

注意 ：经过warping和sin映射后，clock_inputs确实失去了"时钟"的直观含义，变成了"当前处于支撑相或摆动相的某一位置，以及运动方向"（正负号表示上升/下降趋势）。

波形特点：

• 正弦波是周期性的，完美匹配步态周期的循环特性
• 正弦波是平滑的，没有突然的跳跃，有利于神经网络学习
• 正弦波是对称的，上升和下降部分对称，符合步态的运动特性

4.2.3.3 时钟输入的作用

在策略网络中的使用：

• 策略网络接收4个时钟输入（每条腿一个）
• 通过比较不同腿的时钟输入值，策略可以判断：
  • 哪些腿的相位相同（同步运动）
  • 哪些腿的相位相差0.5（交替运动）
  • 当前处于步态周期的哪个阶段

示例 ：在小跑步态中（θcmd=(0.5,0,0)\theta^{cmd} = (0.5, 0, 0)θcmd=(0.5,0,0)）

假设当前tgait=0t_{gait} = 0tgait=0，计算每条腿的相位和时钟输入：

步骤1：计算每条腿的相位

根据小跑步态的相位偏移计算：

• FL（左前）：tFL=tgait+θ1+θ2+θ3=0+0.5+0+0=0.5t_{FL} = t_{gait} + \theta_1 + \theta_2 + \theta_3 = 0 + 0.5 + 0 + 0 = 0.5tFL=tgait+θ1+θ2+θ3=0+0.5+0+0=0.5
• FR（右前）：tFR=tgait+θ2=0+0=0t_{FR} = t_{gait} + \theta_2 = 0 + 0 = 0tFR=tgait+θ2=0+0=0
• RL（左后）：tRL=tgait+θ3=0+0=0t_{RL} = t_{gait} + \theta_3 = 0 + 0 = 0tRL=tgait+θ3=0+0=0
• RR（右后）：tRR=tgait+θ1=0+0.5=0.5t_{RR} = t_{gait} + \theta_1 = 0 + 0.5 = 0.5tRR=tgait+θ1=0+0.5=0.5

步骤2：计算时钟输入

使用公式clockfoot=sin⁡(2π⋅tfoot)clock_{foot} = \sin(2\pi \cdot t_{foot})clockfoot=sin(2π⋅tfoot)：

• FL：clockFL=sin⁡(2π×0.5)=sin⁡(π)=0clock_{FL} = \sin(2\pi \times 0.5) = \sin(\pi) = 0clockFL=sin(2π×0.5)=sin(π)=0
• FR：clockFR=sin⁡(2π×0)=sin⁡(0)=0clock_{FR} = \sin(2\pi \times 0) = \sin(0) = 0clockFR=sin(2π×0)=sin(0)=0
• RL：clockRL=sin⁡(2π×0)=sin⁡(0)=0clock_{RL} = \sin(2\pi \times 0) = \sin(0) = 0clockRL=sin(2π×0)=sin(0)=0
• RR：clockRR=sin⁡(2π×0.5)=sin⁡(π)=0clock_{RR} = \sin(2\pi \times 0.5) = \sin(\pi) = 0clockRR=sin(2π×0.5)=sin(π)=0

结果 ：当tgait=0t_{gait} = 0tgait=0时，所有腿的时钟输入都是0，但它们的相位不同（FR和RL为0，FL和RR为0.5）。

当tgait=0.25t_{gait} = 0.25tgait=0.25时：

步骤1：重新计算相位

• FL：tFL=0.25+0.5=0.75t_{FL} = 0.25 + 0.5 = 0.75tFL=0.25+0.5=0.75
• FR：tFR=0.25+0=0.25t_{FR} = 0.25 + 0 = 0.25tFR=0.25+0=0.25
• RL：tRL=0.25+0=0.25t_{RL} = 0.25 + 0 = 0.25tRL=0.25+0=0.25
• RR：tRR=0.25+0.5=0.75t_{RR} = 0.25 + 0.5 = 0.75tRR=0.25+0.5=0.75

步骤2：计算时钟输入

• FL：clockFL=sin⁡(2π×0.75)=sin⁡(3π/2)=−1clock_{FL} = \sin(2\pi \times 0.75) = \sin(3\pi/2) = -1clockFL=sin(2π×0.75)=sin(3π/2)=−1
• FR：clockFR=sin⁡(2π×0.25)=sin⁡(π/2)=1clock_{FR} = \sin(2\pi \times 0.25) = \sin(\pi/2) = 1clockFR=sin(2π×0.25)=sin(π/2)=1
• RL：clockRL=sin⁡(2π×0.25)=sin⁡(π/2)=1clock_{RL} = \sin(2\pi \times 0.25) = \sin(\pi/2) = 1clockRL=sin(2π×0.25)=sin(π/2)=1
• RR：clockRR=sin⁡(2π×0.75)=sin⁡(3π/2)=−1clock_{RR} = \sin(2\pi \times 0.75) = \sin(3\pi/2) = -1clockRR=sin(2π×0.75)=sin(3π/2)=−1

结果：

• FR和RL的时钟输入 = 111（这两条腿处于上升阶段，相位为0.25）
• FL和RR的时钟输入 = −1-1−1（这两条腿处于下降阶段，相位为0.75）

策略网络的识别：

通过比较不同腿的时钟输入值，策略网络可以识别出：

1. 同步关系：FR和RL的时钟输入相同（都是1），说明它们同步运动
2. 交替关系：FL和RR的时钟输入相同（都是-1），且与FR/RL的符号相反，说明它们交替运动
3. 相位差：FR/RL和FL/RR的时钟输入符号相反，说明它们的相位相差0.5（半个周期）

这种信息帮助策略网络理解步态模式，从而生成协调的运动。

代码实现：

self.clock_inputs[:, 0] = torch.sin(2 * np.pi * foot_indices[0])  # FL
self.clock_inputs[:, 1] = torch.sin(2 * np.pi * foot_indices[1])  # FR
self.clock_inputs[:, 2] = torch.sin(2 * np.pi * foot_indices[2])  # RL
self.clock_inputs[:, 3] = torch.sin(2 * np.pi * foot_indices[3])  # RR

self.doubletime_clock_inputs[:, 0] = torch.sin(4 * np.pi * foot_indices[0])
self.doubletime_clock_inputs[:, 1] = torch.sin(4 * np.pi * foot_indices[1])
self.doubletime_clock_inputs[:, 2] = torch.sin(4 * np.pi * foot_indices[2])
self.doubletime_clock_inputs[:, 3] = torch.sin(4 * np.pi * foot_indices[3])

self.halftime_clock_inputs[:, 0] = torch.sin(np.pi * foot_indices[0])
self.halftime_clock_inputs[:, 1] = torch.sin(np.pi * foot_indices[1])
self.halftime_clock_inputs[:, 2] = torch.sin(np.pi * foot_indices[2])
self.halftime_clock_inputs[:, 3] = torch.sin(np.pi * foot_indices[3])

系统计算了三种频率的时钟输入：

• 标准时钟输入 （clock_inputs）：sin⁡(2π⋅tfoot)\sin(2\pi \cdot t_{foot})sin(2π⋅tfoot)，一个完整周期
• 双倍频时钟输入 （doubletime_clock_inputs）：sin⁡(4π⋅tfoot)\sin(4\pi \cdot t_{foot})sin(4π⋅tfoot)，两个完整周期，提供更细粒度的时序信息
• 半频时钟输入 （halftime_clock_inputs）：sin⁡(π⋅tfoot)\sin(\pi \cdot t_{foot})sin(π⋅tfoot)，半个周期，提供粗粒度的时序信息

这些不同频率的时钟输入提供了多尺度的时序信息 ，有助于解决标准时钟输入的重复值问题（例如，在tfoot=0t_{foot} = 0tfoot=0和tfoot=0.5t_{foot} = 0.5tfoot=0.5时，标准时钟输入都是0，但双倍频时钟输入不同），并帮助策略更好地理解步态周期。

这些时钟输入会被添加到观测向量中，输入到策略网络：

if self.cfg.env.observe_clock_inputs:
    self.obs_buf = torch.cat((self.obs_buf,
                              self.clock_inputs), dim=-1)

4.2.3.4 期望接触状态与时钟输入的联系与区别

共同的基础：

desired_contact_states和clock_inputs都基于相同的foot_indices计算，它们都表示每条腿在步态周期中的位置，但提供的信息和用途不同：

特性	desired_contact_states	clock_inputs
基础变量	foot_indices	foot_indices
计算方式	正态分布CDF平滑函数	正弦波函数
数值范围	0到1	-1到1
主要用途	奖励计算（训练时）	策略输入（推理时）
信息内容	"是否应该接触地面"	"在周期中的位置和趋势"
函数形状	类似平滑方波（0-0.5接近1，0.5-1接近0）	正弦波（0→1→0→-1→0）

关键区别分析：

1. 函数形状的差异：

   • desired_contact_states：形状类似平滑的方波

     • 在tfoot=0t_{foot} = 0tfoot=0时：C≈0.5C \approx 0.5C≈0.5（过渡状态）
     • 在tfoot=0.25t_{foot} = 0.25tfoot=0.25时：C≈1C \approx 1C≈1（支撑相，脚应该接触地面）
     • 在tfoot=0.5t_{foot} = 0.5tfoot=0.5时：C≈0.5C \approx 0.5C≈0.5（过渡状态）
     • 在tfoot=0.75t_{foot} = 0.75tfoot=0.75时：C≈0C \approx 0C≈0（摆动相，脚应该离开地面）
     • 在tfoot=1t_{foot} = 1tfoot=1时：C≈0.5C \approx 0.5C≈0.5（过渡状态）

   • clock_inputs：标准的正弦波

     • 在tfoot=0t_{foot} = 0tfoot=0时：sin⁡(0)=0\sin(0) = 0sin(0)=0
     • 在tfoot=0.25t_{foot} = 0.25tfoot=0.25时：sin⁡(π/2)=1\sin(\pi/2) = 1sin(π/2)=1
     • 在tfoot=0.5t_{foot} = 0.5tfoot=0.5时：sin⁡(π)=0\sin(\pi) = 0sin(π)=0
     • 在tfoot=0.75t_{foot} = 0.75tfoot=0.75时：sin⁡(3π/2)=−1\sin(3\pi/2) = -1sin(3π/2)=−1
     • 在tfoot=1t_{foot} = 1tfoot=1时：sin⁡(2π)=0\sin(2\pi) = 0sin(2π)=0

2. 信息内容的差异：

   • desired_contact_states：

     • 直接回答"这条腿现在应该接触地面吗？"
     • 值接近1表示应该接触，值接近0表示应该离开
     • 在支撑相（0-0.5）接近1，在摆动相（0.5-1）接近0
     • 语义明确：直接对应物理行为（接触/不接触）

   • clock_inputs：

     • 表示"这条腿在周期中的位置"
     • 包含方向信息（正负号表示上升/下降趋势）
     • 在0和0.5处都是0（存在重复值问题）
     • 时序信息丰富：可以推断运动趋势和速度

3. sin函数重复值的问题：

   用户正确指出了sin函数确实存在重复值的问题：

   • sin⁡(0)=sin⁡(π)=0\sin(0) = \sin(\pi) = 0sin(0)=sin(π)=0（在tfoot=0t_{foot} = 0tfoot=0和tfoot=0.5t_{foot} = 0.5tfoot=0.5时）
   • 这意味着仅凭单个时钟输入值，无法区分周期开始（0）和周期中点（0.5）

   解决方案：

   • 系统使用历史观测（30步）来解决这个问题
   • 通过时序信息，策略可以区分"从0开始上升"和"从0.5开始下降"
   • 此外，系统还计算了doubletime_clock_inputs和halftime_clock_inputs，提供不同频率的时钟信号

计算流程总结：

foot_indices (每条腿的相位)
    ↓
    ├─→ 通过CDF函数 → desired_contact_states → 用于奖励计算
    │   (平滑方波形状，语义：是否应该接触)
    │
    └─→ 通过sin函数 → clock_inputs → 用于策略输入
        (正弦波形状，语义：在周期中的位置和趋势)

实际使用示例：

在小跑步态中，当tgait=0t_{gait} = 0tgait=0时：

• FR和RL的相位都是0，所以：
  • desired_contact_states ≈ 0.5（过渡状态，即将进入支撑相）
  • clock_inputs = 0（周期开始）
• FL和RR的相位都是0.5，所以：
  • desired_contact_states ≈ 0.5（过渡状态，即将进入摆动相）
  • clock_inputs = 0（周期中点）

注意 ：虽然此时clock_inputs值相同（都是0），但结合历史观测和多频率时钟输入，策略可以区分它们处于周期的不同阶段（一个在上升，一个在下降）。

总结1：为什么使用clock_inputs而不是desired_contact_states作为策略输入？ 为什么不在观测中使用desired_contact_states？

虽然desired_contact_states也可以表示每条腿在步态周期中的位置，但系统选择使用clock_inputs（正弦波信号）而不是desired_contact_states作为策略网络的输入，原因如下：

• sin 确实会重复取值（单靠 sin(2πt) 不能唯一确定相位），但这里能用是因为 策略吃的是 30 步历史 + 机器人状态 + 4 条腿一起的节拍，能从"上升/下降趋势"消歧。
• desired_contact_states 更像"支撑/摆动的门控 mask "（大段时间饱和在 0 或 1），适合做奖励加权；clock_inputs 更像"连续节拍器"，在半周期内部也持续变化，更适合帮助策略生成平滑的周期动作细节。

代码中的配置：

# if self.cfg.env.observe_desired_contact_states:
#     self.obs_buf = torch.cat((self.obs_buf,
#                               self.desired_contact_states), dim=-1)

可以看到，observe_desired_contact_states选项被注释掉了，说明系统默认不将desired_contact_states作为观测输入。

总结2：为什么使用sin映射而不是直接使用foot_indices？

既然foot_indices已经是0-1之间的周期性值，为什么不直接将其作为策略输入，而要经过sin函数映射？而且，sin映射后似乎失去了"时钟"的直观含义，变成了"当前处于支撑相或摆动相的某一位置"。

代码中的选项：

实际上，系统确实提供了直接使用foot_indices的选项（observe_timing_parameter），但默认是关闭的：

if self.cfg.env.observe_timing_parameter:
    self.obs_buf = torch.cat((self.obs_buf,
                              self.gait_indices.unsqueeze(1)), dim=-1)

这个选项会将全局的gait_indices（而不是每条腿的foot_indices）直接添加到观测中。

为什么使用sin映射？

1. foot_indices 直接输入的问题：0 和 1 是同一时刻，但数值差巨大

foot_indices ∈ [0,1) 是取模相位：0 和 1 代表同一周期起点。但如果你把它当普通实数输入网络，会出现"几何不一致"：

• 真实物理意义上：相位 0.99 和 0.01 非常接近（只差 0.02 个周期）

• 数值上：|0.99 - 0.01| = 0.98 非常远

对 MLP 来说，这会让它很难学出"周期连续"的规律：它得额外学会一个"如果接近 1 也等价于接近 0"的绕行逻辑（本质是学一个环形拓扑），训练更难、更不稳定。

2. sin 映射解决的就是这个"断点"：把线性相位变成"圆上的连续坐标"

映射：
clock(t)=sin⁡(2πt)clock(t)=sin⁡(2πt)clock(t)=sin⁡(2πt)

看刚才那个例子：

• t=0.99：sin⁡(2π⋅0.99)=sin⁡(1.98π)≈−0.0628sin⁡(2π⋅0.99)=sin⁡(1.98π)≈−0.0628sin⁡(2π⋅0.99)=sin⁡(1.98π)≈−0.0628

• t=0.01：sin⁡(2π⋅0.01)=sin⁡(0.02π)≈+0.0628sin⁡(2π⋅0.01)=sin⁡(0.02π)≈+0.0628sin⁡(2π⋅0.01)=sin⁡(0.02π)≈+0.0628

它们在数值上已经变得很接近（幅值都很小），并且跨越周期边界时是连续变化的（从负的小数平滑过到正的小数）。

更本质地说：foot_indices 是"圆周角度 t 的线性刻度"，而 sin(2πt) 是把"圆周角度"投影到一个连续坐标轴上------这就是圆周变量的标准表示方式（circular variable encoding / Fourier feature）。虽然直接使用foot_indices在语义上更直观。

4.2.4 其他关键行为参数

• 步频(fcmdf^{cmd}fcmd): 范围[2.0, 4.0] Hz，表示每只脚每秒接触次数
• 身体高度命令(hzcmdh^{cmd}_zhzcmd): 范围[-0.25, 0.15] m，相对于默认高度0.34m
• 身体俯仰命令(ϕcmd\phi^{cmd}ϕcmd): 范围[-0.4, 0.4] rad
• 脚站立宽度命令(sycmds^{cmd}_ysycmd): 范围[0.10, 0.45] m
• 脚摆动高度命令(hzf,cmdh^{f,cmd}_zhzf,cmd): 范围[0.03, 0.35] m

代码配置：

Cfg.commands.body_height_cmd = [-0.25, 0.15]
Cfg.commands.gait_frequency_cmd_range = [2.0, 4.0]
Cfg.commands.gait_phase_cmd_range = [0.0, 1.0]
Cfg.commands.gait_offset_cmd_range = [0.0, 1.0]
Cfg.commands.gait_bound_cmd_range = [0.0, 1.0]
Cfg.commands.gait_duration_cmd_range = [0.5, 0.5]
Cfg.commands.footswing_height_range = [0.03, 0.35]
Cfg.commands.body_pitch_range = [-0.4, 0.4]
Cfg.commands.body_roll_range = [-0.0, 0.0]
Cfg.commands.stance_width_range = [0.10, 0.45]
Cfg.commands.stance_length_range = [0.35, 0.45]

---

5. 奖励函数设计

奖励函数是实现MoB的核心，分为三类：任务奖励、固定辅助奖励和增强辅助奖励。

5.1 任务奖励 (Task Rewards)

5.1.1 线速度跟踪奖励

公式 ：
rvx,ycmd=exp⁡(−∥vxy−vxycmd∥2/σvxy)r^{v^{cmd}{x,y}} = \exp(-\|v{xy} - v^{cmd}{xy}\|^2/\sigma{v_{xy}})rvx,ycmd=exp(−∥vxy−vxycmd∥2/σvxy)

其中σvxy=0.02\sigma_{v_{xy}} = 0.02σvxy=0.02（tracking_sigma）。

代码实现：

def _reward_tracking_lin_vel(self):
    # Tracking of linear velocity commands (xy axes)
    lin_vel_error = torch.sum(torch.square(self.env.commands[:, :2] - self.env.base_lin_vel[:, :2]), dim=1)
    return torch.exp(-lin_vel_error / self.env.cfg.rewards.tracking_sigma)

5.1.2 角速度跟踪奖励

公式 ：
rωzcmd=exp⁡(−(ωz−ωzcmd)2/σωz)r^{\omega^{cmd}_z} = \exp(-(\omega_z - \omega^{cmd}z)^2/\sigma{\omega_z})rωzcmd=exp(−(ωz−ωzcmd)2/σωz)

代码实现：

def _reward_tracking_ang_vel(self):
    # Tracking of angular velocity commands (yaw)
    ang_vel_error = torch.square(self.env.commands[:, 2] - self.env.base_ang_vel[:, 2])
    return torch.exp(-ang_vel_error / self.env.cfg.rewards.tracking_sigma_yaw)

5.2 固定辅助奖励 (Fixed Auxiliary Rewards)

这些奖励与行为参数无关，旨在提高整体稳定性和sim-to-real迁移能力。

5.2.1 基础稳定性奖励

1. z轴速度惩罚 ：
   rvz=−0.02×vz2r^{v_z} = -0.02 \times v_z^2rvz=−0.02×vz2

   代码实现：

   def _reward_lin_vel_z(self):
       # Penalize z axis base linear velocity
       return torch.square(self.env.base_lin_vel[:, 2])

2. 滚动-俯仰角速度惩罚 ：
   rωxy=−0.001×∥ωxy∥2r^{\omega_{xy}} = -0.001 \times \|\omega_{xy}\|^2rωxy=−0.001×∥ωxy∥2

   代码实现：

   def _reward_ang_vel_xy(self):
       # Penalize xy axes base angular velocity
       return torch.sum(torch.square(self.env.base_ang_vel[:, :2]), dim=1)

3. 姿态惩罚 ：
   rorientation=−5.0×∥gproj,xy∥2r^{orientation} = -5.0 \times \|g_{proj,xy}\|^2rorientation=−5.0×∥gproj,xy∥2

   代码实现：

   def _reward_orientation(self):
       # Penalize non flat base orientation
       return torch.sum(torch.square(self.env.projected_gravity[:, :2]), dim=1)

5.2.2 动作平滑性奖励

1. 动作变化率惩罚 （_reward_action_rate）：
   raction_rate=−0.01×∥at−1−at∥2r^{action\rate} = -0.01 \times \|a{t-1} - a_t\|^2raction_rate=−0.01×∥at−1−at∥2

   代码实现：

   def _reward_action_rate(self):
       # Penalize changes in actions
       return torch.sum(torch.square(self.env.last_actions - self.env.actions), dim=1)

   惩罚相邻时刻动作的变化，鼓励平滑的动作。

2. 动作平滑性惩罚（一阶） （_reward_action_smoothness_1）：
   rsmoothness_1=−0.1×∥qtarget,t−1−qtarget,t∥2r^{smoothness\1} = -0.1 \times \|q{target,t-1} - q_{target,t}\|^2rsmoothness_1=−0.1×∥qtarget,t−1−qtarget,t∥2

   代码实现：

   def _reward_action_smoothness_1(self):
       # Penalize changes in actions
       diff = torch.square(self.env.joint_pos_target[:, :self.env.num_actuated_dof] - self.env.last_joint_pos_target[:, :self.env.num_actuated_dof])
       diff = diff * (self.env.last_actions[:, :self.env.num_dof] != 0)  # ignore first step
       return torch.sum(diff, dim=1)

   惩罚相邻时刻目标关节位置的变化，鼓励平滑的动作。

3. 动作平滑性惩罚（二阶） （_reward_action_smoothness_2）：
   rsmoothness_2=−0.1×∥at−2−2at−1+at∥2r^{smoothness\2} = -0.1 \times \|a{t-2} - 2a_{t-1} + a_t\|^2rsmoothness_2=−0.1×∥at−2−2at−1+at∥2

   代码实现：

   def _reward_action_smoothness_2(self):
       # Penalize changes in actions
       diff = torch.square(self.env.joint_pos_target[:, :self.env.num_actuated_dof] - 2 * self.env.last_joint_pos_target[:, :self.env.num_actuated_dof] + self.env.last_last_joint_pos_target[:, :self.env.num_actuated_dof])
       diff = diff * (self.env.last_actions[:, :self.env.num_dof] != 0)  # ignore first step
       diff = diff * (self.env.last_last_actions[:, :self.env.num_dof] != 0)  # ignore second step
       return torch.sum(diff, dim=1)

5.2.3 脚滑移惩罚

什么是脚滑移？ 当脚接触地面时，如果脚在水平方向（x-y平面）有速度，说明脚在滑动。这会导致：

1. 能量损失：滑动会产生摩擦，消耗能量
2. 控制困难：滑动使机器人难以精确控制位置
3. 不稳定：滑动可能导致机器人失去平衡

为什么需要惩罚脚滑移？ 在理想情况下，当脚接触地面时，脚应该相对于地面静止（速度为0）。惩罚脚滑移可以鼓励策略学习"将脚牢牢地放在地面上"的行为。

代码实现详解：

def _reward_feet_slip(self):
    contact = self.env.contact_forces[:, self.env.feet_indices, 2] > 1.
    contact_filt = torch.logical_or(contact, self.env.last_contacts)
    self.env.last_contacts = contact
    foot_velocities = torch.square(torch.norm(self.env.foot_velocities[:, :, 0:2], dim=2).view(self.env.num_envs, -1))
    rew_slip = torch.sum(contact_filt * foot_velocities, dim=1)
    return rew_slip

逐步解释：

1. 检测脚是否接触地面：

   contact = self.env.contact_forces[:, self.env.feet_indices, 2] > 1.

   • contact_forces[:, feet_indices, 2]：获取每条脚在z方向（垂直向上）的接触力，feet_indices与之前每条腿的相位foot_indices不同
   • > 1.：如果接触力大于1牛顿，认为脚接触地面
   • contact：一个布尔张量，形状为[num_envs, 4]，表示每条脚是否接触地面

2. 使用接触状态过滤：

   contact_filt = torch.logical_or(contact, self.env.last_contacts)
   self.env.last_contacts = contact

   • last_contacts：上一时刻的接触状态
   • torch.logical_or(contact, self.env.last_contacts)：如果当前或上一时刻脚接触地面，都认为脚在接触状态
   • 为什么这样做？ 避免在接触状态切换的瞬间（脚刚接触或刚离开）漏掉惩罚，确保惩罚的连续性

3. 计算脚的水平速度：

   foot_velocities = torch.square(torch.norm(self.env.foot_velocities[:, :, 0:2], dim=2).view(self.env.num_envs, -1))

   • foot_velocities[:, :, 0:2]：获取每条脚在x和y方向的速度（水平速度）
   • torch.norm(..., dim=2)：计算每条脚的水平速度大小（vx2+vy2\sqrt{v_x^2 + v_y^2}vx2+vy2 ）
   • torch.square(...)：对速度大小取平方（vxy2v_{xy}^2vxy2）
   • .view(self.env.num_envs, -1)：重塑为[num_envs, 4]的形状
   • 结果 ：foot_velocities[i, j]表示第i个环境中第j条脚的水平速度平方

4. 计算惩罚：

   rew_slip = torch.sum(contact_filt * foot_velocities, dim=1)

   • contact_filt * foot_velocities：只有当脚接触地面时（contact_filt = True），才计算速度惩罚
   • torch.sum(..., dim=1)：对4条脚求和，得到每个环境的总惩罚
   • 结果 ：rew_slip[i]表示第i个环境的脚滑移惩罚

数学表达 ：
rslip=∑foot=141contact(foot)×∥vxyfoot∥2r^{slip} = \sum_{foot=1}^{4} \mathbf{1}{contact}(foot) \times \|v^{foot}{xy}\|^2rslip=foot=1∑41contact(foot)×∥vxyfoot∥2

其中1contact(foot)\mathbf{1}_{contact}(foot)1contact(foot)表示脚是否接触地面（1或0）。

奖励权重 ：在代码配置中，脚滑移惩罚的权重为-0.04，即：
Rslip=−0.04×rslipR^{slip} = -0.04 \times r^{slip}Rslip=−0.04×rslip

直观理解：

• 当脚接触地面且水平速度为0时：惩罚为0（理想情况）
• 当脚接触地面但水平速度为0.5 m/s时：惩罚为0.04×0.25=0.010.04 \times 0.25 = 0.010.04×0.25=0.01（较小惩罚）
• 当脚接触地面但水平速度为1.0 m/s时：惩罚为0.04×1.0=0.040.04 \times 1.0 = 0.040.04×1.0=0.04（较大惩罚）
• 当脚不接触地面时：无论速度多大，惩罚都为0（因为contact_filt = False）

5.2.4 关节相关惩罚

1. 关节位置惩罚 （_reward_dof_pos）：
   rdof_pos=−∑i=112(qi−qdefault,i)2r^{dof\pos} = -\sum{i=1}^{12} (q_i - q_{default,i})^2rdof_pos=−i=1∑12(qi−qdefault,i)2

   代码实现：

   def _reward_dof_pos(self):
       # Penalize dof positions
       return torch.sum(torch.square(self.env.dof_pos - self.env.default_dof_pos), dim=1)

   惩罚关节位置偏离默认位置，鼓励机器人保持接近默认姿态。

2. 关节速度惩罚 （_reward_dof_vel）：
   rdof_vel=−0.0001×∑i=112q˙i2r^{dof\vel} = -0.0001 \times \sum{i=1}^{12} \dot{q}_i^2rdof_vel=−0.0001×i=1∑12q˙i2

   代码实现：

   def _reward_dof_vel(self):
       # Penalize dof velocities
       return torch.sum(torch.square(self.env.dof_vel), dim=1)

   惩罚关节速度，鼓励平滑运动。

3. 关节加速度惩罚 （_reward_dof_acc）：
   rdof_acc=−∑i=112(q˙i,t−1−q˙i,tdt)2r^{dof\acc} = -\sum{i=1}^{12} \left(\frac{\dot{q}{i,t-1} - \dot{q}{i,t}}{dt}\right)^2rdof_acc=−i=1∑12(dtq˙i,t−1−q˙i,t)2

   代码实现：

   def _reward_dof_acc(self):
       # Penalize dof accelerations
       return torch.sum(torch.square((self.env.last_dof_vel - self.env.dof_vel) / self.env.dt), dim=1)

   惩罚关节加速度，鼓励更平滑的运动。

4. 关节限制违反惩罚 （_reward_dof_pos_limits）：
   rdof_limits=−10.0×∑i=1121qi>qmax∥∥qi<qminr^{dof\limits} = -10.0 \times \sum{i=1}^{12} \mathbf{1}{q_i>q{max}\|\|q_i<q_{min}}rdof_limits=−10.0×i=1∑121qi>qmax∥∥qi<qmin

   代码实现：

   def _reward_dof_pos_limits(self):
       # Penalize dof positions too close to the limit
       out_of_limits = -(self.env.dof_pos - self.env.dof_pos_limits[:, 0]).clip(max=0.)  # lower limit
       out_of_limits += (self.env.dof_pos - self.env.dof_pos_limits[:, 1]).clip(min=0.)
       return torch.sum(out_of_limits, dim=1)

   惩罚关节位置超出限制范围。

5. 关节扭矩惩罚 （_reward_torques）：
   rtorques=−0.0001×∑i=112τi2r^{torques} = -0.0001 \times \sum_{i=1}^{12} \tau_i^2rtorques=−0.0001×i=1∑12τi2

   代码实现：

   def _reward_torques(self):
       # Penalize torques
       return torch.sum(torch.square(self.env.torques), dim=1)

   惩罚关节扭矩，鼓励使用较小的力。

5.2.5 碰撞和接触相关惩罚

1. 碰撞惩罚 （_reward_collision）：
   rcollision=−5.0×∑body1∥fbody∥>0.1r^{collision} = -5.0 \times \sum_{body} \mathbf{1}{\|f{body}\| > 0.1}rcollision=−5.0×body∑1∥fbody∥>0.1

   代码实现：

   def _reward_collision(self):
       # Penalize collisions on selected bodies
       return torch.sum(1. * (torch.norm(self.env.contact_forces[:, self.env.penalised_contact_indices, :], dim=-1) > 0.1),
                        dim=1)

   惩罚大腿/小腿等非脚部部位的碰撞。

2. 脚接触力过大惩罚 （_reward_feet_contact_forces）：
   rcontact_forces=−∑footmax⁡(0,∥ffoot∥−fmax)r^{contact\forces} = -\sum{foot} \max(0, \|f_{foot}\| - f_{max})rcontact_forces=−foot∑max(0,∥ffoot∥−fmax)

   代码实现：

   def _reward_feet_contact_forces(self):
       # penalize high contact forces
       return torch.sum((torch.norm(self.env.contact_forces[:, self.env.feet_indices, :],
                                    dim=-1) - self.env.cfg.rewards.max_contact_force).clip(min=0.), dim=1)

   惩罚脚部接触力过大，避免过度用力。

3. 脚接触速度惩罚 （_reward_feet_contact_vel）：
   rcontact_vel=−∑foot1near_ground×∥vfoot∥2r^{contact\vel} = -\sum{foot} \mathbf{1}_{near\_ground} \times \|v^{foot}\|^2rcontact_vel=−foot∑1near_ground×∥vfoot∥2

   代码实现：

   def _reward_feet_contact_vel(self):
       reference_heights = 0
       near_ground = self.env.foot_positions[:, :, 2] - reference_heights < 0.03
       foot_velocities = torch.square(torch.norm(self.env.foot_velocities[:, :, 0:3], dim=2).view(self.env.num_envs, -1))
       rew_contact_vel = torch.sum(near_ground * foot_velocities, dim=1)
       return rew_contact_vel

   惩罚脚接近地面时的速度，鼓励脚在接触地面时保持静止。

4. 脚冲击速度惩罚 （_reward_feet_impact_vel）：
   rimpact_vel=−∑foot1contact×max⁡(0,−vzfoot)2r^{impact\vel} = -\sum{foot} \mathbf{1}_{contact} \times \max(0, -v^{foot}_z)^2rimpact_vel=−foot∑1contact×max(0,−vzfoot)2

   代码实现：

   def _reward_feet_impact_vel(self):
       prev_foot_velocities = self.env.prev_foot_velocities[:, :, 2].view(self.env.num_envs, -1)
       contact_states = torch.norm(self.env.contact_forces[:, self.env.feet_indices, :], dim=-1) > 1.0
       
       rew_foot_impact_vel = contact_states * torch.square(torch.clip(prev_foot_velocities, -100, 0))
       
       return torch.sum(rew_foot_impact_vel, dim=1)

   惩罚脚接触地面时的向下冲击速度，鼓励轻柔落地。

5.3 增强辅助奖励 (Augmented Auxiliary Rewards)

这些奖励与行为参数直接相关，用于强制策略按照指定的行为参数执行。

5.3.1 摆动相位跟踪奖励（力）

问题背景：在步态周期中，每条腿都有两个阶段：

• 支撑相：脚应该接触地面，产生接触力
• 摆动相：脚应该离开地面，不应该有接触力

为什么需要这个奖励？ 如果策略在摆动相时脚仍然接触地面，说明：

1. 脚没有及时抬起，可能导致绊倒
2. 步态模式不正确，无法实现期望的步态
3. 能量效率低，脚在地面上拖行会产生摩擦

目标：当脚应该处于摆动阶段时，鼓励零接触力。

代码实现详解：

def _reward_tracking_contacts_shaped_force(self):
    foot_forces = torch.norm(self.env.contact_forces[:, self.env.feet_indices, :], dim=-1)
    desired_contact = self.env.desired_contact_states

    reward = 0
    for i in range(4):
        reward += - (1 - desired_contact[:, i]) * (
                    1 - torch.exp(-1 * foot_forces[:, i] ** 2 / self.env.cfg.rewards.gait_force_sigma))
    return reward / 4

逐步解释：

1. 计算每条脚的接触力大小：

   foot_forces = torch.norm(self.env.contact_forces[:, self.env.feet_indices, :], dim=-1)

   • contact_forces[:, feet_indices, :]：获取每条脚的3维接触力向量（x, y, z方向）
   • torch.norm(..., dim=-1)：计算每条脚的接触力大小（fx2+fy2+fz2\sqrt{f_x^2 + f_y^2 + f_z^2}fx2+fy2+fz2 ）
   • 结果 ：foot_forces[i, j]表示第i个环境中第j条脚的接触力大小（单位：牛顿）

2. 获取期望接触状态：

   desired_contact = self.env.desired_contact_states

   • desired_contact[i, j]：第i个环境中第j条脚的期望接触状态（0到1之间）
   • 接近1表示应该接触地面，接近0表示应该离开地面

3. 对每条脚计算奖励：

   for i in range(4):
       reward += - (1 - desired_contact[:, i]) * (
                   1 - torch.exp(-1 * foot_forces[:, i] ** 2 / self.env.cfg.rewards.gait_force_sigma))

   让我们逐步分解这个公式：

   a. (1 - desired_contact[:, i])：

   • 当desired_contact = 0（应该摆动）时，这个值为1，会计算惩罚
   • 当desired_contact = 1（应该支撑）时，这个值为0，不会计算惩罚
   • 作用：只在摆动相时计算奖励

   b. foot_forces[:, i] ** 2：

   • 接触力的平方

   c. torch.exp(-1 * foot_forces[:, i] ** 2 / gait_force_sigma)：

   • gait_force_sigma = 100.0：控制惩罚的陡峭程度
   • 这是一个指数衰减函数 ：
     • 当foot_forces = 0时：exp(0) = 1
     • 当foot_forces = 10时：exp(-100/100) = exp(-1) ≈ 0.37
     • 当foot_forces = 20时：exp(-400/100) = exp(-4) ≈ 0.018
   • 特点：接触力越大，这个值越小（接近0）

   d. 1 - torch.exp(...)：

   • 当接触力为0时：1 - 1 = 0（无惩罚，理想情况）
   • 当接触力为10N时：1 - 0.37 = 0.63（中等惩罚）
   • 当接触力为20N时：1 - 0.018 = 0.982（大惩罚）
   • 特点：接触力越大，惩罚越大，但惩罚有上限（最大为1）

   e. - (1 - desired_contact) * (1 - exp(...))：

   • 负号表示这是惩罚（奖励为负）
   • 只在摆动相时（1 - desired_contact = 1）计算惩罚
   • 惩罚大小取决于接触力

4. 平均化：

   return reward / 4

   • 将4条脚的奖励求和后除以4，得到平均奖励

数学表达 ：
rcfcmd=−14∑foot=14[1−Cfootcmd]×(1−exp⁡(−∥ffoot∥2σcf))r^{c^{cmd}f} = -\frac{1}{4} \sum{foot=1}^{4} [1 - C^{cmd}{foot}] \times \left(1 - \exp\left(-\frac{\|f{foot}\|^2}{\sigma_{cf}}\right)\right)rcfcmd=−41foot=1∑4[1−Cfootcmd]×(1−exp(−σcf∥ffoot∥2))

其中：

• CfootcmdC^{cmd}_{foot}Cfootcmd：期望接触状态（0到1）
• ffootf_{foot}ffoot：实际接触力向量
• σcf=100.0\sigma_{cf} = 100.0σcf=100.0：gait_force_sigma

奖励权重 ：在代码配置中，这个奖励的权重为-0.08，即：
Rcfcmd=−0.08×rcfcmdR^{c^{cmd}_f} = -0.08 \times r^{c^{cmd}_f}Rcfcmd=−0.08×rcfcmd

直观理解（以一条脚为例）：

• 情况1 ：脚应该摆动（desired_contact = 0），实际接触力为0N

  • 奖励 = −0.08×1×(1−1)=0-0.08 \times 1 \times (1 - 1) = 0−0.08×1×(1−1)=0（无惩罚，理想情况）

• 情况2 ：脚应该摆动（desired_contact = 0），实际接触力为10N

  • 奖励 = −0.08×1×(1−0.37)=−0.05-0.08 \times 1 \times (1 - 0.37) = -0.05−0.08×1×(1−0.37)=−0.05（中等惩罚）

• 情况3 ：脚应该摆动（desired_contact = 0），实际接触力为20N

  • 奖励 = −0.08×1×(1−0.018)=−0.078-0.08 \times 1 \times (1 - 0.018) = -0.078−0.08×1×(1−0.018)=−0.078（大惩罚）

• 情况4 ：脚应该支撑（desired_contact = 1），无论接触力多大

  • 奖励 = −0.08×0×(...)=0-0.08 \times 0 \times (...) = 0−0.08×0×(...)=0（不计算惩罚，因为这是支撑相）

为什么使用指数函数而不是线性函数？

• 指数函数提供了平滑的惩罚曲线，避免在接触力很小时产生过大的梯度
• 当接触力接近0时，惩罚也接近0，有利于策略学习"完全抬起脚"的行为
• 当接触力很大时，惩罚接近上限，避免过度惩罚导致训练不稳定

5.3.2 支撑相位跟踪奖励（速度）

问题背景：在步态周期中，当脚处于支撑相时，脚应该：

• 接触地面
• 相对于地面保持静止（速度为0）

为什么需要这个奖励？ 如果策略在支撑相时脚在地面上滑动，说明：

1. 脚没有牢牢抓住地面，可能导致打滑
2. 步态模式不正确，无法实现稳定的支撑
3. 能量效率低，滑动会产生摩擦损失

目标：当脚应该处于支撑阶段时，鼓励脚在地面上保持静止（水平速度为0）。

代码实现详解：

def _reward_tracking_contacts_shaped_vel(self):
    foot_velocities = torch.norm(self.env.foot_velocities, dim=2).view(self.env.num_envs, -1)
    desired_contact = self.env.desired_contact_states
    reward = 0
    for i in range(4):
        reward += - (desired_contact[:, i] * (
                    1 - torch.exp(-1 * foot_velocities[:, i] ** 2 / self.env.cfg.rewards.gait_vel_sigma)))
    return reward / 4

逐步解释：

1. 计算每条脚的速度大小：

   foot_velocities = torch.norm(self.env.foot_velocities, dim=2).view(self.env.num_envs, -1)

   • foot_velocities：每条脚的3维速度向量（x, y, z方向）
   • torch.norm(..., dim=2)：计算每条脚的速度大小（vx2+vy2+vz2\sqrt{v_x^2 + v_y^2 + v_z^2}vx2+vy2+vz2 ）
   • .view(self.env.num_envs, -1)：重塑为[num_envs, 4]的形状
   • 结果 ：foot_velocities[i, j]表示第i个环境中第j条脚的速度大小（单位：m/s）

2. 获取期望接触状态：

   desired_contact = self.env.desired_contact_states

   • 与摆动相位跟踪奖励相同，desired_contact[i, j]表示第i个环境中第j条脚的期望接触状态

3. 对每条脚计算奖励：

   for i in range(4):
       reward += - (desired_contact[:, i] * (
                   1 - torch.exp(-1 * foot_velocities[:, i] ** 2 / self.env.cfg.rewards.gait_vel_sigma)))

   让我们逐步分解这个公式：

   a. desired_contact[:, i]：

   • 当desired_contact = 1（应该支撑）时，这个值为1，会计算惩罚
   • 当desired_contact = 0（应该摆动）时，这个值为0，不会计算惩罚
   • 作用：只在支撑相时计算奖励

   b. foot_velocities[:, i] ** 2：

   • 脚速度的平方

   c. torch.exp(-1 * foot_velocities[:, i] ** 2 / gait_vel_sigma)：

   • gait_vel_sigma = 10.0：控制惩罚的陡峭程度（注意：这个值比gait_force_sigma小，说明对速度更敏感）
   • 这是一个指数衰减函数 ：
     • 当foot_velocities = 0时：exp(0) = 1
     • 当foot_velocities = 1 m/s时：exp(-1/10) = exp(-0.1) ≈ 0.90
     • 当foot_velocities = 2 m/s时：exp(-4/10) = exp(-0.4) ≈ 0.67
     • 当foot_velocities = 3 m/s时：exp(-9/10) = exp(-0.9) ≈ 0.41
   • 特点：速度越大，这个值越小（接近0）

   d. 1 - torch.exp(...)：

   • 当速度为0时：1 - 1 = 0（无惩罚，理想情况）
   • 当速度为1 m/s时：1 - 0.90 = 0.10（小惩罚）
   • 当速度为2 m/s时：1 - 0.67 = 0.33（中等惩罚）
   • 当速度为3 m/s时：1 - 0.41 = 0.59（大惩罚）
   • 特点：速度越大，惩罚越大，但惩罚有上限（最大为1）

   e. - desired_contact * (1 - exp(...))：

   • 负号表示这是惩罚（奖励为负）
   • 只在支撑相时（desired_contact = 1）计算惩罚
   • 惩罚大小取决于脚的速度

4. 平均化：

   return reward / 4

   • 将4条脚的奖励求和后除以4，得到平均奖励

数学表达 ：
rcvcmd=−14∑foot=14Cfootcmd×(1−exp⁡(−∥vfoot∥2σcv))r^{c^{cmd}v} = -\frac{1}{4} \sum{foot=1}^{4} C^{cmd}{foot} \times \left(1 - \exp\left(-\frac{\|v^{foot}\|^2}{\sigma{cv}}\right)\right)rcvcmd=−41foot=1∑4Cfootcmd×(1−exp(−σcv∥vfoot∥2))

其中：

• CfootcmdC^{cmd}_{foot}Cfootcmd：期望接触状态（0到1）
• vfootv^{foot}vfoot：实际脚速度向量
• σcv=10.0\sigma_{cv} = 10.0σcv=10.0：gait_vel_sigma

奖励权重 ：在代码配置中，这个奖励的权重为-0.08，即：
Rcvcmd=−0.08×rcvcmdR^{c^{cmd}_v} = -0.08 \times r^{c^{cmd}_v}Rcvcmd=−0.08×rcvcmd

直观理解（以一条脚为例）：

• 情况1 ：脚应该支撑（desired_contact = 1），实际速度为0 m/s

  • 奖励 = −0.08×1×(1−1)=0-0.08 \times 1 \times (1 - 1) = 0−0.08×1×(1−1)=0（无惩罚，理想情况）

• 情况2 ：脚应该支撑（desired_contact = 1），实际速度为1 m/s

  • 奖励 = −0.08×1×(1−0.90)=−0.008-0.08 \times 1 \times (1 - 0.90) = -0.008−0.08×1×(1−0.90)=−0.008（小惩罚）

• 情况3 ：脚应该支撑（desired_contact = 1），实际速度为2 m/s

  • 奖励 = −0.08×1×(1−0.67)=−0.026-0.08 \times 1 \times (1 - 0.67) = -0.026−0.08×1×(1−0.67)=−0.026（中等惩罚）

• 情况4 ：脚应该支撑（desired_contact = 1），实际速度为3 m/s

  • 奖励 = −0.08×1×(1−0.41)=−0.047-0.08 \times 1 \times (1 - 0.41) = -0.047−0.08×1×(1−0.41)=−0.047（大惩罚）

• 情况5 ：脚应该摆动（desired_contact = 0），无论速度多大

  • 奖励 = −0.08×0×(...)=0-0.08 \times 0 \times (...) = 0−0.08×0×(...)=0（不计算惩罚，因为这是摆动相）

为什么gait_vel_sigma比gait_force_sigma小？

• gait_vel_sigma = 10.0（速度）
• gait_force_sigma = 100.0（力）
• 原因：速度的测量更直接、更准确，所以可以使用更小的sigma值，使惩罚更敏感
• 力的测量可能受到噪声影响，使用较大的sigma值可以提供更平滑的惩罚曲线

5.3.3 身体高度跟踪奖励

公式 ：
rhzcmd=−(hz−(hzcmd+htarget))2r^{h^{cmd}_z} = -(h_z - (h^{cmd}z + h{target}))^2rhzcmd=−(hz−(hzcmd+htarget))2

其中htarget=0.30h_{target} = 0.30htarget=0.30 m是基础高度目标。

代码实现：

def _reward_jump(self):
    reference_heights = 0
    body_height = self.env.base_pos[:, 2] - reference_heights
    jump_height_target = self.env.commands[:, 3] + self.env.cfg.rewards.base_height_target
    reward = - torch.square(body_height - jump_height_target)
    return reward

说明：这个奖励鼓励机器人将身体高度调整到命令指定的高度（相对于基础高度0.30m）。

#### 5.3.4 Raibert启发式脚放置奖励

##### 5.3.4.1 什么是Raibert启发式？

**Raibert启发式（Raibert Heuristic）**是由Marc Raibert在1980年代提出的一个经典的四足机器人控制算法。它的核心思想是：**为了保持平衡和实现期望速度，脚应该放在哪里？**

**核心问题**：当机器人想要以某个速度移动时，脚应该放在什么位置才能：
1. 保持身体平衡
2. 实现期望的移动速度
3. 为下一步运动做好准备

##### 5.3.4.2 基本原理

**直观理解**：想象你在跑步时：
- 如果你想加速，你会把脚放在身体**后面**一点，这样身体会向前倾斜，产生向前的力
- 如果你想减速，你会把脚放在身体**前面**一点，这样身体会向后倾斜，产生向后的力
- 如果你想保持匀速，你会把脚放在身体**正下方**

**数学表达**：Raibert启发式的基本公式是：
$$p^{desired}_{foot} = p^{nominal}_{foot} + K \times (v^{desired} - v^{current}) \times T_{stance}$$

其中：
- $p^{nominal}_{foot}$：脚的标称位置（静止站立时的位置）
- $v^{desired}$：期望速度
- $v^{current}$：当前速度
- $T_{stance}$：支撑相持续时间
- $K$：比例系数

**物理意义**：
- 如果当前速度小于期望速度，脚应该放在标称位置**后面**，帮助加速
- 如果当前速度大于期望速度，脚应该放在标称位置**前面**，帮助减速
- 偏移量 = 速度差 × 支撑时间

##### 5.3.4.3 在本系统中的实现

系统使用Raibert启发式来计算**期望的脚放置位置**，然后通过奖励函数鼓励策略将脚放在这个位置。

**步骤1：计算基础站立位置**

首先，根据行为参数中的站立宽度$s^{cmd}_y$和站立长度，计算四条腿的标称位置（在机器人本体坐标系中）：

从上方俯视（机器人本体坐标系）：

前

FL ● ● FR

-----|-----

RL ● ● RR

后

- **站立宽度**：左右脚之间的距离（$s^{cmd}_y$）
- **站立长度**：前后脚之间的距离（默认0.45m）

标称位置：
- FR（右前）：$(L/2, s^{cmd}_y/2)$
- FL（左前）：$(L/2, -s^{cmd}_y/2)$
- RR（右后）：$(-L/2, s^{cmd}_y/2)$
- RL（左后）：$(-L/2, -s^{cmd}_y/2)$

**代码实现**：
```877:889:go1_gym/envs/rewards/corl_rewards.py
if self.env.cfg.commands.num_commands >= 13:
    desired_stance_width = self.env.commands[:, 12:13]
    desired_ys_nom = torch.cat([desired_stance_width / 2, -desired_stance_width / 2, desired_stance_width / 2, -desired_stance_width / 2], dim=1)
else:
    desired_stance_width = 0.3
    desired_ys_nom = torch.tensor([desired_stance_width / 2,  -desired_stance_width / 2, desired_stance_width / 2, -desired_stance_width / 2], device=self.env.device).unsqueeze(0)

if self.env.cfg.commands.num_commands >= 14:
    desired_stance_length = self.env.commands[:, 13:14]
    desired_xs_nom = torch.cat([desired_stance_length / 2, desired_stance_length / 2, -desired_stance_length / 2, -desired_stance_length / 2], dim=1)
else:
    desired_stance_length = 0.45
    desired_xs_nom = torch.tensor([desired_stance_length / 2,  desired_stance_length / 2, -desired_stance_length / 2, -desired_stance_length / 2], device=self.env.device).unsqueeze(0)

步骤2：计算速度相关的偏移

根据期望速度和当前步态相位，计算脚的偏移量：

X方向（前后）偏移 ：
Δx=phase×vxcmd×0.5fcmd\Delta x = phase \times v^{cmd}_x \times \frac{0.5}{f^{cmd}}Δx=phase×vxcmd×fcmd0.5

其中：

• phasephasephase：当前腿的相位（-0.5到0.5之间，支撑相为负，摆动相为正）
• vxcmdv^{cmd}_xvxcmd：期望的前进速度
• fcmdf^{cmd}fcmd：步频
• 0.5fcmd\frac{0.5}{f^{cmd}}fcmd0.5：支撑相持续时间（假设支撑相占50%周期）

物理意义：

• 当腿处于支撑相时（phase<0phase < 0phase<0），如果期望前进，脚应该放在标称位置后面 （Δx<0\Delta x < 0Δx<0），帮助推动身体前进
• 当腿处于摆动相时（phase>0phase > 0phase>0），脚应该放在标称位置前面 （Δx>0\Delta x > 0Δx>0），为下一步做准备

Y方向（左右）偏移 （用于转弯）：
Δy=phase×ωzcmd×L2×0.5fcmd\Delta y = phase \times \omega^{cmd}_z \times \frac{L}{2} \times \frac{0.5}{f^{cmd}}Δy=phase×ωzcmd×2L×fcmd0.5

其中：

• ωzcmd\omega^{cmd}_zωzcmd：期望的偏航角速度（转弯速度）
• L2\frac{L}{2}2L：站立长度的一半（转弯半径）

物理意义：

• 当期望左转时（ωzcmd>0\omega^{cmd}_z > 0ωzcmd>0），右腿应该放在更外侧，左腿放在更内侧
• 当期望右转时（ωzcmd<0\omega^{cmd}_z < 0ωzcmd<0），左腿应该放在更外侧，右腿放在更内侧

代码实现：

# raibert offsets
phases = torch.abs(1.0 - (self.env.foot_indices * 2.0)) * 1.0 - 0.5
frequencies = self.env.commands[:, 4]
x_vel_des = self.env.commands[:, 0:1]
yaw_vel_des = self.env.commands[:, 2:3]
y_vel_des = yaw_vel_des * desired_stance_length / 2
desired_ys_offset = phases * y_vel_des * (0.5 / frequencies.unsqueeze(1))
desired_ys_offset[:, 2:4] *= -1  # 后腿的y方向偏移取反
desired_xs_offset = phases * x_vel_des * (0.5 / frequencies.unsqueeze(1))

desired_ys_nom = desired_ys_nom + desired_ys_offset
desired_xs_nom = desired_xs_nom + desired_xs_offset

步骤3：计算期望脚位置

期望脚位置 = 标称位置 + 速度偏移：
pfootdesired=pfootnominal+[Δx,Δy]p^{desired}{foot} = p^{nominal}{foot} + [\Delta x, \Delta y]pfootdesired=pfootnominal+[Δx,Δy]

步骤4：计算奖励

奖励函数惩罚实际脚位置与期望位置的偏差：

公式 ：
rraibert=−10.0×∑foot∥pfootactual−pfootdesired∥2r^{raibert} = -10.0 \times \sum_{foot} \|p^{actual}{foot} - p^{desired}{foot}\|^2rraibert=−10.0×foot∑∥pfootactual−pfootdesired∥2

代码实现：

desired_footsteps_body_frame = torch.cat((desired_xs_nom.unsqueeze(2), desired_ys_nom.unsqueeze(2)), dim=2)

err_raibert_heuristic = torch.abs(desired_footsteps_body_frame - footsteps_in_body_frame[:, :, 0:2])

reward = torch.sum(torch.square(err_raibert_heuristic), dim=(1, 2))

return reward

5.3.4.4 为什么使用Raibert启发式？

问题：为什么不简单地固定脚的位置？

答案：固定脚位置会导致以下问题：

1. 无法适应速度变化：当机器人需要加速或减速时，固定位置无法提供必要的力
2. 转弯困难：固定位置无法实现有效的转弯
3. 平衡问题：在动态运动中，固定位置可能导致不平衡

Raibert启发式的优势：

1. 物理合理：基于倒立摆模型，符合物理规律
2. 自适应：根据期望速度自动调整脚位置
3. 简单有效：计算简单，但效果显著

在本系统中的作用：

• 通过奖励函数，策略学习将脚放在Raibert启发式计算的位置
• 这样策略既能完成速度跟踪任务，又能保持平衡
• 同时考虑了行为参数（如站立宽度），使步态更加多样化

5.3.5 脚摆动高度跟踪奖励

公式 ：
rhzf,cmd=−30.0×∑foot(hzf−hzf,cmd)2×(1−Cfootcmd)r^{h^{f,cmd}z} = -30.0 \times \sum{foot} (h^f_z - h^{f,cmd}z)^2 \times (1 - C^{cmd}{foot})rhzf,cmd=−30.0×foot∑(hzf−hzf,cmd)2×(1−Cfootcmd)

仅在摆动阶段（1−Cfootcmd=11 - C^{cmd}_{foot} = 11−Cfootcmd=1）惩罚脚高度偏差。

代码实现：

def _reward_feet_clearance_cmd_linear(self):
    phases = 1 - torch.abs(1.0 - torch.clip((self.env.foot_indices * 2.0) - 1.0, 0.0, 1.0) * 2.0)
    foot_height = (self.env.foot_positions[:, :, 2]).view(self.env.num_envs, -1)# - reference_heights
    target_height = self.env.commands[:, 9].unsqueeze(1) * phases + 0.02 # offset for foot radius 2cm
    rew_foot_clearance = torch.square(target_height - foot_height) * (1 - self.env.desired_contact_states)
    return torch.sum(rew_foot_clearance, dim=1)

5.3.6 身体俯仰跟踪奖励

公式 ：
rϕcmd=−5.0×(ϕ−ϕcmd)2r^{\phi^{cmd}} = -5.0 \times (\phi - \phi^{cmd})^2rϕcmd=−5.0×(ϕ−ϕcmd)2

代码实现：

def _reward_orientation_control(self):
    # Penalize non flat base orientation
    roll_pitch_commands = self.env.commands[:, 10:12]
    quat_roll = quat_from_angle_axis(-roll_pitch_commands[:, 1],
                                     torch.tensor([1, 0, 0], device=self.env.device, dtype=torch.float))
    quat_pitch = quat_from_angle_axis(-roll_pitch_commands[:, 0],
                                      torch.tensor([0, 1, 0], device=self.env.device, dtype=torch.float))

    desired_base_quat = quat_mul(quat_roll, quat_pitch)
    desired_projected_gravity = quat_rotate_inverse(desired_base_quat, self.env.gravity_vec)

    return torch.sum(torch.square(self.env.projected_gravity[:, :2] - desired_projected_gravity[:, :2]), dim=1)

5.4 奖励组合策略

为防止辅助奖励压倒任务奖励，系统采用创新的奖励组合方式：
rtotal=rtask×exp⁡(caux×raux)r_{total} = r_{task} \times \exp(c_{aux} \times r_{aux})rtotal=rtask×exp(caux×raux)

其中：

• rtaskr_{task}rtask：任务奖励的总和（正值）
• rauxr_{aux}raux：辅助奖励的总和（负值）
• caux=0.02c_{aux} = 0.02caux=0.02：缩放参数

代码配置：

Cfg.rewards.only_positive_rewards = False
Cfg.rewards.only_positive_rewards_ji22_style = True
Cfg.rewards.sigma_rew_neg = 0.02

这种设计确保：

1. 机器人总是因任务进展而获得奖励
2. 当辅助目标被满足时获得更多奖励
3. 当辅助目标不满足时获得较少奖励，但不会完全抵消任务进展

5.5 奖励函数完整总结

5.5.1 任务奖励 (Task Rewards)

奖励函数	代码函数名	权重	参数值	是否使用	说明
线速度跟踪	_reward_tracking_lin_vel	1.0	tracking_sigma = 0.02	✓	跟踪x-y方向线速度命令
角速度跟踪	_reward_tracking_ang_vel	0.5	tracking_sigma_yaw	✓	跟踪yaw角速度命令

5.5.2 固定辅助奖励 (Fixed Auxiliary Rewards)

奖励函数	代码函数名	权重	参数值	是否使用	说明
z轴速度惩罚	_reward_lin_vel_z	-0.02	-	✓	惩罚垂直方向速度
滚动-俯仰角速度惩罚	_reward_ang_vel_xy	-0.001	-	✓	惩罚滚动和俯仰角速度
姿态惩罚	_reward_orientation	0.0	-	✗	惩罚非水平姿态（未使用）
动作变化率惩罚	_reward_action_rate	-0.01	-	✓	惩罚动作变化
动作平滑性1	_reward_action_smoothness_1	-0.1	-	✓	惩罚一阶动作变化
动作平滑性2	_reward_action_smoothness_2	-0.1	-	✓	惩罚二阶动作变化
脚滑移惩罚	_reward_feet_slip	-0.04	-	✓	惩罚脚接触地面时的水平速度
关节位置惩罚	_reward_dof_pos	0.0	-	✗	惩罚关节位置偏离默认值（未使用）
关节速度惩罚	_reward_dof_vel	-0.0001	-	✓	惩罚关节速度
关节加速度惩罚	_reward_dof_acc	-	-	✗	惩罚关节加速度（未使用）
关节限制违反惩罚	_reward_dof_pos_limits	-10.0	-	✓	惩罚关节位置超出限制
关节扭矩惩罚	_reward_torques	-0.0001	-	✓	惩罚关节扭矩
碰撞惩罚	_reward_collision	-5.0	-	✓	惩罚非脚部部位碰撞
脚接触力过大惩罚	_reward_feet_contact_forces	0.0	max_contact_force	✗	惩罚脚接触力过大（未使用）
脚接触速度惩罚	_reward_feet_contact_vel	-	-	✗	惩罚脚接近地面时的速度（未使用）
脚冲击速度惩罚	_reward_feet_impact_vel	0.0	-	✗	惩罚脚落地冲击速度（未使用）

5.5.3 增强辅助奖励 (Augmented Auxiliary Rewards)

奖励函数	代码函数名	权重	参数值	是否使用	说明
身体高度跟踪	_reward_jump	10.0	base_height_target = 0.30 m	✓	跟踪身体高度命令
摆动相位跟踪（力）	_reward_tracking_contacts_shaped_force	4.0	gait_force_sigma = 100.0	✓	摆动相时鼓励零接触力
支撑相位跟踪（速度）	_reward_tracking_contacts_shaped_vel	4.0	gait_vel_sigma = 10.0	✓	支撑相时鼓励脚静止
脚摆动高度跟踪	_reward_feet_clearance_cmd_linear	-30.0	-	✓	跟踪脚摆动高度命令
身体姿态控制	_reward_orientation_control	-5.0	-	✓	跟踪身体俯仰和滚动角命令
Raibert启发式	_reward_raibert_heuristic	-10.0	-	✓	鼓励脚放在Raibert启发式计算的位置

注意：

• 权重为0.0或未列出的奖励函数在训练中未使用
• 所有使用的奖励函数权重都在scripts/train.py中配置
• 增强辅助奖励的权重通常较大，因为它们直接关系到行为参数的执行

---

6. 训练过程

6.1 策略架构

• 主策略网络（Body）：三层MLP，隐藏层大小[512, 256, 128]，使用ELU激活函数
• 域参数估计器（Adaptation Module）：两层MLP，隐藏层大小[256, 128]，使用ELU激活函数，用于预测机器人速度和地面摩擦
• 输入：30步历史观察（2100维）+ 潜在变量（2维，来自adaptation module）
• 输出：12个关节的目标位置偏移

6.2 训练配置

关键训练参数（代码配置）：

Cfg.env.num_privileged_obs = 2
Cfg.env.num_observation_history = 30
Cfg.reward_scales.feet_contact_forces = 0.0

Cfg.domain_rand.rand_interval_s = 4
Cfg.commands.num_commands = 15
Cfg.env.observe_two_prev_actions = True
Cfg.env.observe_yaw = False
Cfg.env.num_observations = 70
Cfg.env.num_scalar_observations = 70
Cfg.env.observe_gait_commands = True
Cfg.env.observe_timing_parameter = False
Cfg.env.observe_clock_inputs = True

6.3 域随机化

为提高sim-to-real迁移能力，系统随机化以下参数：

代码配置：

Cfg.domain_rand.lag_timesteps = 6
Cfg.domain_rand.randomize_lag_timesteps = True
Cfg.control.control_type = "actuator_net"

Cfg.domain_rand.randomize_rigids_after_start = False
Cfg.env.priv_observe_motion = False
Cfg.env.priv_observe_gravity_transformed_motion = False
Cfg.domain_rand.randomize_friction_indep = False
Cfg.env.priv_observe_friction_indep = False
Cfg.domain_rand.randomize_friction = True
Cfg.env.priv_observe_friction = True
Cfg.domain_rand.friction_range = [0.1, 3.0]
Cfg.domain_rand.randomize_restitution = True
Cfg.env.priv_observe_restitution = True
Cfg.domain_rand.restitution_range = [0.0, 0.4]
Cfg.domain_rand.randomize_base_mass = True
Cfg.env.priv_observe_base_mass = False
Cfg.domain_rand.added_mass_range = [-1.0, 3.0]
Cfg.domain_rand.randomize_gravity = True
Cfg.domain_rand.gravity_range = [-1.0, 1.0]
Cfg.domain_rand.gravity_rand_interval_s = 8.0
Cfg.domain_rand.gravity_impulse_duration = 0.99
Cfg.env.priv_observe_gravity = False
Cfg.domain_rand.randomize_com_displacement = False
Cfg.domain_rand.com_displacement_range = [-0.15, 0.15]
Cfg.env.priv_observe_com_displacement = False
Cfg.domain_rand.randomize_ground_friction = True
Cfg.env.priv_observe_ground_friction = False
Cfg.env.priv_observe_ground_friction_per_foot = False
Cfg.domain_rand.ground_friction_range = [0.0, 0.0]
Cfg.domain_rand.randomize_motor_strength = True
Cfg.domain_rand.motor_strength_range = [0.9, 1.1]
Cfg.env.priv_observe_motor_strength = False
Cfg.domain_rand.randomize_motor_offset = True
Cfg.domain_rand.motor_offset_range = [-0.02, 0.02]
Cfg.env.priv_observe_motor_offset = False

6.3.1 域随机化参数完整列表

参数类别	参数名称	随机化范围	是否启用	是否作为特权观测	说明
系统延迟	lag_timesteps	6步	✓	-	控制延迟时间步数
物理属性
基座质量	added_mass_range	[-1.0, 3.0] kg	✓	✗	添加到基座的质量
重心偏移	com_displacement_range	[-0.15, 0.15] m	✗	✗	重心位置偏移（未启用）
地面属性
地面摩擦	friction_range	[0.1, 3.0]	✓	✓	地面摩擦系数
地面恢复系数	restitution_range	[0.0, 0.4]	✓	✓	地面弹性恢复系数
地面摩擦（独立）	-	-	✗	✗	每只脚独立摩擦（未启用）
地面摩擦（全局）	ground_friction_range	[0.0, 0.0]	✓	✗	全局地面摩擦（范围为零，实际未随机化）
电机属性
电机强度	motor_strength_range	[0.9, 1.1]	✓	✗	电机扭矩缩放因子
电机位置偏移	motor_offset_range	[-0.02, 0.02] rad	✓	✗	电机位置编码器偏移
PD增益因子	Kp_factor_range	[0.8, 1.3]	✗	✗	PD比例增益因子（未启用）
PD阻尼因子	Kd_factor_range	[0.5, 1.5]	✗	✗	PD微分增益因子（未启用）
环境属性
重力	gravity_range	[-1.0, 1.0] m/s²	✓	✗	重力加速度偏移
重力随机化间隔	gravity_rand_interval_s	8.0秒	✓	-	重力随机化的时间间隔
重力脉冲持续时间	gravity_impulse_duration	0.99	✓	-	重力脉冲持续时间比例
其他
刚体随机化	randomize_rigids_after_start	-	✗	-	启动后随机化刚体（未启用）
推机器人	push_robots	-	✗	-	随机推机器人（未启用）

说明：

• 是否启用：表示该参数是否在训练中随机化
• 是否作为特权观测：表示该参数是否作为特权信息提供给adaptation module（仅在训练时可用）
• 大多数物理参数都启用了随机化，但不作为特权观测，迫使策略学习鲁棒的行为
• 只有摩擦和恢复系数作为特权观测，帮助adaptation module估计环境特性

6.4 任务与行为采样

6.4.1 训练时的行为参数采样

重要说明 ：在训练时，行为参数是自动采样的，不需要人工指定。系统使用**自适应课程学习（Adaptive Curriculum Learning）**来自动调整参数范围。

采样机制：

1. 自动采样频率：

   Cfg.commands.resampling_time = 10

   • 每10秒重新采样一次任务和行为参数
   • 这意味着在每个训练episode中，行为参数会保持不变，直到episode结束或10秒后重新采样

2. 自适应课程学习：

   def _resample_commands(self, env_ids):
       # ... 更新课程学习 ...
       for i, (category, curriculum) in enumerate(zip(self.category_names, self.curricula)):
           # ... 根据性能更新课程 ...
           curriculum.update(old_bins, task_rewards, success_thresholds, ...)
       
       # ... 从课程中采样新命令 ...
       new_commands, new_bin_inds = curriculum.sample(batch_size=batch_size)

   • 系统根据策略的性能自动调整参数范围
   • 如果策略在某个参数范围内表现良好，会逐渐增加难度（扩大参数范围）
   • 如果策略表现不佳，会缩小参数范围，让策略更容易学习

3. 步态类型采样：

   if self.cfg.commands.gaitwise_curricula:
       for i, (category, env_ids_in_category) in enumerate(zip(self.category_names, category_env_ids)):
           if category == "pronk":  # pronking
               self.commands[env_ids_in_category, 5] = ...
           elif category == "trot":  # trotting
               self.commands[env_ids_in_category, 5] = self.commands[env_ids_in_category, 5] / 2 + 0.25
               self.commands[env_ids_in_category, 6] = 0
               self.commands[env_ids_in_category, 7] = 0
           elif category == "pace":  # pacing
               ...
           elif category == "bound":  # bounding
               ...

   • 系统会自动从不同的步态类型中采样（跳跃、小跑、踱步、跳跃）
   • 每种步态类型对应不同的相位偏移参数设置

4. 其他行为参数采样：

   • 步频 ：从[2.0, 4.0] Hz范围内均匀采样
   • 身体高度 ：从[-0.25, 0.15] m范围内均匀采样
   • 脚摆动高度 ：从[0.03, 0.35] m范围内均匀采样
   • 身体俯仰角 ：从[-0.4, 0.4] rad范围内均匀采样
   • 站立宽度 ：从[0.10, 0.45] m范围内均匀采样

总结 ：训练时，行为参数完全由系统自动采样，不需要人工干预。系统会根据训练进度自动调整参数范围，确保策略能够学习到多样化的行为。

6.4.2 部署时的行为参数设置

重要说明 ：在部署时，行为参数需要人工指定 或通过遥控器输入 。系统不会根据环境地形自动调整行为参数。

设置方式：

1. 通过遥控器实时调整（默认方式）：

   class RCControllerProfile(CommandProfile):
       def __init__(self, dt, state_estimator, x_scale=1.0, y_scale=1.0, yaw_scale=1.0, ...):
           self.state_estimator = state_estimator
           ...
       
       def get_command(self, t, probe=False):
           command = self.state_estimator.get_command()
           command[0] = command[0] * self.x_scale
           command[1] = command[1] * self.y_scale
           command[2] = command[2] * self.yaw_scale
           ...
           return command, reset_timer

   • 操作员通过遥控器输入速度命令（vx,vy,ωzv_x, v_y, \omega_zvx,vy,ωz）
   • 行为参数（步态类型、身体高度等）需要单独设置，通常通过代码或配置文件指定
   • 遥控器主要控制任务命令（速度），而不是行为参数

2. 通过预设命令配置文件：

   class ElegantGaitProfile(CommandProfile):
       def __init__(self, dt, filename):
           with open(f'../command_profiles/{filename}', 'r') as file:
                   command_sequence = json.load(file)
           
           self.commands[:len_command_sequence, 0] = torch.Tensor(command_sequence["x_vel_cmd"])
           self.commands[:len_command_sequence, 2] = torch.Tensor(command_sequence["yaw_vel_cmd"])
           self.commands[:len_command_sequence, 3] = torch.Tensor(command_sequence["height_cmd"])
           self.commands[:len_command_sequence, 4] = torch.Tensor(command_sequence["frequency_cmd"])
           self.commands[:len_command_sequence, 5] = torch.Tensor(command_sequence["offset_cmd"])
           self.commands[:len_command_sequence, 6] = torch.Tensor(command_sequence["phase_cmd"])
           self.commands[:len_command_sequence, 7] = torch.Tensor(command_sequence["bound_cmd"])
           self.commands[:len_command_sequence, 8] = torch.Tensor(command_sequence["duration_cmd"])

   • 可以创建JSON配置文件，预设完整的行为参数序列
   • 包括速度命令和所有行为参数（身体高度、步频、相位偏移等）

3. 通过代码直接设置：

   command_profile = RCControllerProfile(dt=control_dt, state_estimator=se, x_scale=max_vel, y_scale=0.6, yaw_scale=max_yaw_vel)

   • 在部署脚本中，可以设置速度缩放参数
   • 但行为参数（如步态类型）通常需要在LCM消息或配置文件中设置

如何指定行为参数？

方法1：修改部署代码（推荐用于固定行为参数）：

# 在部署脚本中，可以创建一个自定义的CommandProfile
class CustomGaitProfile(CommandProfile):
    def __init__(self, dt):
        super().__init__(dt)
        # 设置固定的行为参数
        self.commands[:, 3] = 0.0  # 身体高度命令
        self.commands[:, 4] = 3.0  # 步频（Hz）
        self.commands[:, 5] = 0.5  # 相位偏移1（小跑步态）
        self.commands[:, 6] = 0.0  # 相位偏移2
        self.commands[:, 7] = 0.0  # 相位偏移3
        self.commands[:, 8] = 0.5  # 支撑相持续时间
        self.commands[:, 9] = 0.15 # 脚摆动高度
        # ... 其他参数 ...

方法2：通过LCM消息动态设置（推荐用于实时调整）：

• 系统可以通过LCM消息接收行为参数
• 操作员可以通过上位机软件实时调整参数
• 需要修改LCMAgent类来接收和处理这些消息

方法3：使用预设配置文件（推荐用于复杂行为序列）：

• 创建JSON文件，定义完整的行为参数序列
• 使用ElegantGaitProfile加载配置文件
• 适合预定义的运动模式（如"爬楼梯模式"、"过障碍模式"）

实际部署示例：

假设你想让机器人在部署时使用小跑步态，可以这样设置：

# 在部署脚本中
command_profile = RCControllerProfile(dt=control_dt, state_estimator=se, ...)

# 方法1：如果使用自定义CommandProfile
class TrottingProfile(RCControllerProfile):
    def get_command(self, t, probe=False):
        command, reset_timer = super().get_command(t, probe)
        # 覆盖行为参数为小跑步态
        command[3] = 0.0      # 身体高度
        command[4] = 3.0      # 步频
        command[5] = 0.5      # 相位偏移1（小跑）
        command[6] = 0.0      # 相位偏移2
        command[7] = 0.0      # 相位偏移3
        command[8] = 0.5      # 支撑相持续时间
        return command, reset_timer

command_profile = TrottingProfile(dt=control_dt, state_estimator=se, ...)

重要限制：

1. 系统不会自动调整 ：部署时，行为参数不会根据环境地形自动调整。如果遇到障碍物，操作员需要手动调整身体高度、脚摆动高度等参数。

2. 需要操作员经验：操作员需要理解每个行为参数的作用，并根据环境选择合适的参数值。

3. 实时调整困难：虽然可以通过LCM消息实时调整，但需要额外的上位机软件支持。

未来改进方向（论文中提到）：

• 使用分层学习，让高层策略自动选择行为参数
• 从人类演示中学习参数选择策略
• 基于环境感知自动调整参数

6.5 训练算法

• 算法：PPO (Proximal Policy Optimization)
• 训练迭代：100,000次迭代
• 评估频率：每100次迭代评估一次

代码调用：

env = HistoryWrapper(env)
gpu_id = 0
runner = Runner(env, device=f"cuda:{gpu_id}")
runner.learn(num_learning_iterations=100000, init_at_random_ep_len=True, eval_freq=100)

---

7. 部署与实时控制

7.1 部署架构

部署系统使用**LCM (Lightweight Communications and Marshalling)**进行实时通信：

• 状态估计器（State Estimator）：从IMU和关节编码器估计机器人状态
• LCM Agent：封装策略网络和动作发布
• 命令配置文件（Command Profile）：定义预定义的运动序列

7.2 状态估计

状态估计器功能：

• 从IMU获取姿态和角速度
• 从关节编码器获取关节位置和速度
• 估计基座线速度（通过运动学）
• 检测脚部接触状态

代码实现（部署时）：

def get_obs(self):
    self.dof_pos = self.se.get_joint_positions()
    self.dof_vel = self.se.get_joint_velocities()
    self.gravity_vector = self.se.get_gravity_vector()
    self.body_linear_vel = self.se.get_body_linear_vel()
    self.body_angular_vel = self.se.get_body_angular_vel()

    ob = np.concatenate((self.gravity_vector.reshape(1, -1),
                         self.commands * self.commands_scale,
                         (self.dof_pos - self.default_dof_pos).reshape(1, -1) * self.obs_scales["dof_pos"],
                         self.dof_vel.reshape(1, -1) * self.obs_scales["dof_vel"],
                         torch.clip(self.actions, -self.cfg["normalization"]["clip_actions"],
                                    self.cfg["normalization"]["clip_actions"]).cpu().detach().numpy().reshape(1, -1)
                         ), axis=1)

    if self.cfg["env"]["observe_two_prev_actions"]:
        ob = np.concatenate((ob,
                        self.last_actions.cpu().detach().numpy().reshape(1, -1)), axis=1)

    if self.cfg["env"]["observe_clock_inputs"]:
        ob = np.concatenate((ob,
                        self.clock_inputs), axis=1)

7.3 动作发布

部署时将动作转换为PD目标并通过LCM发布：

代码实现：

def publish_action(self, action, hard_reset=False):

    command_for_robot = pd_tau_targets_lcmt()
    self.joint_pos_target = \
        (action[0, :12].detach().cpu().numpy() * self.cfg["control"]["action_scale"]).flatten()
    self.joint_pos_target[[0, 3, 6, 9]] *= self.cfg["control"]["hip_scale_reduction"]
    self.joint_pos_target = self.joint_pos_target
    self.joint_pos_target += self.default_dof_pos
    joint_pos_target = self.joint_pos_target[self.joint_idxs]
    self.joint_vel_target = np.zeros(12)

    command_for_robot.q_des = joint_pos_target
    command_for_robot.qd_des = self.joint_vel_target
    command_for_robot.kp = self.p_gains
    command_for_robot.kd = self.d_gains
    command_for_robot.tau_ff = np.zeros(12)
    command_for_robot.se_contactState = np.zeros(4)
    command_for_robot.timestamp_us = int(time.time() * 10 ** 6)
    command_for_robot.id = 0

    if hard_reset:
        command_for_robot.id = -1


    self.torques = (self.joint_pos_target - self.dof_pos) * self.p_gains + (self.joint_vel_target - self.dof_vel) * self.d_gains

    lc.publish("pd_plustau_targets", command_for_robot.encode())

7.4 步态相位更新（部署时）

部署时同样需要更新步态相位和时钟输入：

代码实现：

# clock accounting
frequencies = self.commands[:, 4]
phases = self.commands[:, 5]
offsets = self.commands[:, 6]
if self.num_commands == 8:
    bounds = 0
    durations = self.commands[:, 7]
else:
    bounds = self.commands[:, 7]
    durations = self.commands[:, 8]
self.gait_indices = torch.remainder(self.gait_indices + self.dt * frequencies, 1.0)

if "pacing_offset" in self.cfg["commands"] and self.cfg["commands"]["pacing_offset"]:
    self.foot_indices = [self.gait_indices + phases + offsets + bounds,
                         self.gait_indices + bounds,
                         self.gait_indices + offsets,
                         self.gait_indices + phases]
else:
    self.foot_indices = [self.gait_indices + phases + offsets + bounds,
                         self.gait_indices + offsets,
                         self.gait_indices + bounds,
                         self.gait_indices + phases]
self.clock_inputs[:, 0] = torch.sin(2 * np.pi * self.foot_indices[0])
self.clock_inputs[:, 1] = torch.sin(2 * np.pi * self.foot_indices[1])
self.clock_inputs[:, 2] = torch.sin(2 * np.pi * self.foot_indices[2])

7.5 部署流程

部署脚本：

def load_and_run_policy(label, experiment_name, max_vel=1.0, max_yaw_vel=1.0):
    # load agent
    dirs = glob.glob(f"../../runs/{label}/*")
    logdir = sorted(dirs)[0]

    with open(logdir+"/parameters.pkl", 'rb') as file:
        pkl_cfg = pkl.load(file)
        print(pkl_cfg.keys())
        cfg = pkl_cfg["Cfg"]
        print(cfg.keys())


    se = StateEstimator(lc)

    control_dt = 0.02
    command_profile = RCControllerProfile(dt=control_dt, state_estimator=se, x_scale=max_vel, y_scale=0.6, yaw_scale=max_yaw_vel)

    hardware_agent = LCMAgent(cfg, se, command_profile)
    se.spin()

    from go1_gym_deploy.envs.history_wrapper import HistoryWrapper
    hardware_agent = HistoryWrapper(hardware_agent)

    policy = load_policy(logdir)

    # load runner
    root = f"{pathlib.Path(__file__).parent.resolve()}/../../logs/"
    pathlib.Path(root).mkdir(parents=True, exist_ok=True)
    deployment_runner = DeploymentRunner(experiment_name=experiment_name, se=None,
                                         log_root=f"{root}/{experiment_name}")
    deployment_runner.add_control_agent(hardware_agent, "hardware_closed_loop")
    deployment_runner.add_policy(policy)
    deployment_runner.add_command_profile(command_profile)

    if len(sys.argv) >= 2:
        max_steps = int(sys.argv[1])
    else:
        max_steps = 10000000
    print(f'max steps {max_steps}')

    deployment_runner.run(max_steps=max_steps, logging=True)

策略加载：

def load_policy(logdir):
    body = torch.jit.load(logdir + '/checkpoints/body_latest.jit')
    import os
    adaptation_module = torch.jit.load(logdir + '/checkpoints/adaptation_module_latest.jit')

    def policy(obs, info):
        i = 0
        latent = adaptation_module.forward(obs["obs_history"].to('cpu'))
        action = body.forward(torch.cat((obs["obs_history"].to('cpu'), latent), dim=-1))
        info['latent'] = latent
        return action

    return policy

---

8. 关键创新点总结

1. 条件策略设计:

   • 通过行为参数btb_tbt条件化策略，使单一策略能生成多样化行为
   • 避免了训练多个独立策略的计算成本

2. 奖励结构创新:

   • 三类奖励(任务、固定辅助、增强辅助)的精心设计
   • rtaskexp⁡(cauxraux)r_{task}\exp(c_{aux}r_{aux})rtaskexp(cauxraux)组合确保任务目标不被辅助目标淹没

3. 物理启发的行为参数化:

   • 基于生物力学原理设计行为参数(步态相位、Raibert启发式)
   • 使参数具有直观物理意义，便于人类理解和调整

4. 无需重新训练的适应性:

   • 通过实时调整行为参数，适应分布外环境
   • 显著减少针对新环境的迭代训练需求

5. 执行器网络建模:

   • 使用神经网络精确建模真实电机行为，提高sim-to-real迁移能力

6. 历史观测与域随机化:

   • 30步历史观测提供时序信息
   • 广泛的域随机化提高鲁棒性

---

9. 方法限制与权衡

9.1 任务性能与行为多样性的权衡

MoB方法在训练环境中会略微降低任务性能，这是行为多样性与任务性能之间的固有权衡：

• 步态约束限制：强制遵循特定步态模式（如小跑、跳跃）会限制机器人在某些任务上的最优性能

  • 例如：在平地冲刺任务中，固定步态可能不如自由步态灵活
  • 行为参数化要求策略同时满足任务目标和行为约束，可能产生次优解

• 高速运动限制 ：热图分析显示，行为参数化对高速直线+旋转组合运动存在限制

  • 当同时要求高线速度和角速度时，某些步态配置可能无法满足
  • 例如：小跑步态在高速转弯时可能不如其他步态稳定

• 计算开销：虽然单一策略避免了训练多个策略，但：

  • 策略网络需要处理额外的行为参数输入（15维命令向量）
  • 历史观测维度增加（30步×70维=2100维）
  • 奖励计算更复杂（增强辅助奖励需要实时计算期望接触状态）

代码体现：训练配置中可以看到行为参数的采样范围限制了某些极端行为：

Cfg.commands.body_height_cmd = [-0.25, 0.15]
Cfg.commands.gait_frequency_cmd_range = [2.0, 4.0]
Cfg.commands.footswing_height_range = [0.03, 0.35]
Cfg.commands.body_pitch_range = [-0.4, 0.4]
Cfg.commands.stance_width_range = [0.10, 0.45]

这些范围限制了机器人的运动能力，但同时也确保了训练稳定性和sim-to-real迁移。

9.2 行为参数化限制

当前的行为参数化设计虽然覆盖了大部分常见步态，但仍存在以下限制：

9.2.1 无法表达的行为

• 单腿行为：当前参数化假设四足协调运动，无法表达单腿跳跃、三腿支撑等非对称行为
• 特技动作：后空翻、侧翻等需要复杂时序协调的动作超出了当前参数化范围
• 动态平衡行为：某些需要快速重心转移的极端行为可能无法通过当前参数表达

9.2.2 行为空间盲区

行为参数空间存在"盲区"，即某些参数组合可能：

• 物理不可行：例如，极高的步频（>4Hz）配合极低的脚摆动高度可能导致脚无法及时抬起
• 训练不足：某些参数组合在训练中采样频率低，策略可能未充分学习
• 参数冲突 ：多个行为参数同时调整时可能产生冲突，例如：
  • 高身体高度 + 宽站立宽度 + 高步频可能超出关节运动范围
  • 极端俯仰角 + 高速运动可能导致不稳定

代码体现：步态相位偏移的计算方式限制了可能的步态组合：

def _step_contact_targets(self):
    if self.cfg.env.observe_gait_commands:
        frequencies = self.commands[:, 4]
        phases = self.commands[:, 5]
        offsets = self.commands[:, 6]
        bounds = self.commands[:, 7]
        durations = self.commands[:, 8]
        self.gait_indices = torch.remainder(self.gait_indices + self.dt * frequencies, 1.0)

这种基于固定公式的计算方式无法表达更复杂的步态时序模式。

9.2.3 参数化设计假设

当前参数化基于以下假设，这些假设限制了行为空间：

1. 周期性假设：假设所有步态都是周期性的，无法表达非周期性或自适应步态
2. 对称性假设：左右对称的步态更容易表达，非对称步态受限
3. 线性组合假设：行为参数通过线性组合影响步态，无法表达非线性交互

9.3 人类依赖性

9.3.1 当前系统的依赖

系统目前需要人类操作员手动调整行为参数，这带来了以下限制：

• 实时调整需求：操作员需要根据环境变化实时调整参数

  • 例如：遇到障碍物时需要降低身体高度、增加脚摆动高度
  • 需要快速响应和操作经验

• 参数选择困难：15维行为参数空间中，操作员需要理解每个参数的影响

  • 参数之间存在交互作用，调整一个参数可能影响其他行为
  • 缺乏直观的"最佳参数"指导

• 部署复杂性：部署系统需要：

  • 状态估计器准确估计机器人状态
  • LCM通信稳定可靠
  • 操作员熟悉遥控器映射和参数调整界面

代码体现：部署时的命令配置需要操作员通过遥控器输入：

command_profile = RCControllerProfile(dt=control_dt, state_estimator=se, x_scale=max_vel, y_scale=0.6, yaw_scale=max_yaw_vel)

9.3.2 未来改进方向

论文和代码中暗示了以下可能的改进方向：

1. 分层学习：

   • 高层策略自动选择行为参数
   • 低层策略执行具体运动
   • 减少人类干预需求

2. 人类演示学习：

   • 从人类操作中学习参数选择策略
   • 使用模仿学习或逆强化学习
   • 自动适应不同环境

3. 自适应参数调整：

   • 基于环境感知自动调整行为参数
   • 使用强化学习优化参数选择
   • 实现完全自主的行为切换

4. 简化参数空间：

   • 减少参数维度或使用参数降维
   • 提供预设行为模式（如"爬楼梯模式"、"过障碍模式"）
   • 降低操作复杂度

9.4 其他技术限制

9.4.1 仿真到现实的差距

尽管使用了广泛的域随机化和执行器网络，仍存在sim-to-real差距：

• 传感器噪声：真实IMU和编码器的噪声模式可能与仿真不同
• 延迟建模：虽然建模了20ms延迟，但真实系统的延迟可能更复杂
• 地面特性：真实地面的摩擦、弹性等特性难以完全模拟

9.4.2 计算资源需求

• 训练时间：100,000次迭代需要大量计算资源
• 实时推理：部署时需要实时运行策略网络和adaptation module
• 历史观测存储：30步历史观测需要额外的内存和计算

9.4.3 可扩展性限制

• 其他机器人平台：当前设计针对Go1优化，扩展到其他机器人需要重新设计参数化
• 更复杂任务：当前主要关注速度跟踪，扩展到更复杂任务（如操作、导航）需要额外设计