RAG与向量余弦距离：深入理解大语言模型背后的数学原理

引言

近年来，大型语言模型（LLM）取得了令人瞩目的成就，但它们仍然存在一些固有的局限性，例如知识截止（knowledge cutoff）和幻觉（hallucination）。为了解决这些问题，研究人员提出了一种名为"检索增强生成"（Retrieval-Augmented Generation，简称RAG）的技术。RAG通过从外部知识库中检索相关信息来增强LLM的生成能力，从而提高了生成内容的准确性和时效性。

在RAG的核心机制中，向量嵌入（vector embedding）和余弦距离（cosine distance）扮演着至关重要的角色。本文将深入探讨RAG的工作原理，并重点介绍向量余弦距离的数学概念及其在RAG中的应用。

什么是RAG？

RAG是一种将检索（retrieval）和生成（generation）相结合的技术。其核心思想是，在生成文本之前，首先从一个大型的知识库（如维基百科、公司内部文档等）中检索出与用户输入相关的信息，然后将这些信息作为上下文（context）提供给语言模型，引导其生成更准确、更丰富的回答。

RAG的工作流程可以概括为以下几个步骤：

编码（Encoding）：将用户输入（query）和知识库中的文档都编码成高维向量，这些向量被称为"嵌入"（embeddings）。
检索（Retrieval）：使用向量相似度计算方法，在知识库中找到与用户输入向量最相似的文档向量。
生成（Generation）：将检索到的文档内容与原始的用户输入拼接在一起，形成一个增强的提示（prompt），然后将其输入到语言模型中，生成最终的回答。

向量余弦距离

在RAG的检索步骤中，如何判断两个向量的相似度呢？答案就是余弦距离。

余弦距离，也称为余弦相似度，是用来衡量两个向量方向上的差异。在几何上，它可以被解释为两个向量夹角的余弦值。如果两个向量的方向完全相同，它们的余弦相似度为1；如果它们的方向完全相反，余弦相似度为-1；如果它们相互垂直，余弦相似度为0。余弦距离就是1减去这个余弦值，所以夹角越小，余弦距离越近。

余弦距离的数学公式

给定两个向量 A 和 B ，它们之间的余弦相似度 cosine_similarity 可以通过以下公式计算：

cosine_similarity ( A , B ) = A ⋅ B ∥ A ∥ ∥ B ∥ = ∑ i = 1 n A i B i ∑ i = 1 n A i 2 ∑ i = 1 n B i 2 \text{cosine\similarity}(A, B) = \frac{A \cdot B}{\|A\| \|B\|} = \frac{\sum{i=1}^{n} A_i B_i}{\sqrt{\sum_{i=1}^{n} A_i^2} \sqrt{\sum_{i=1}^{n} B_i^2}} cosine_similarity(A,B)=∥A∥∥B∥A⋅B=∑i=1nAi2 ∑i=1nBi2 ∑i=1nAiBi

其中：

A · B 是向量 A 和 B 的点积。
||A|| 和 ||B|| 分别是向量 A 和 B 的欧几里得范数（或长度）。
n 是向量的维度。

2维空间中的余弦相似度

如果向量 A = (x1, y1) 和 B = (x2, y2)，则公式为：

cosine_similarity ( A , B ) = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 x 2 2 + y 2 2 \text{cosine\_similarity}(A, B) = \frac{x_1 x_2 + y_1 y_2}{\sqrt{x_1^2 + y_1^2} \sqrt{x_2^2 + y_2^2}} cosine_similarity(A,B)=x12+y12 x22+y22 x1x2+y1y2

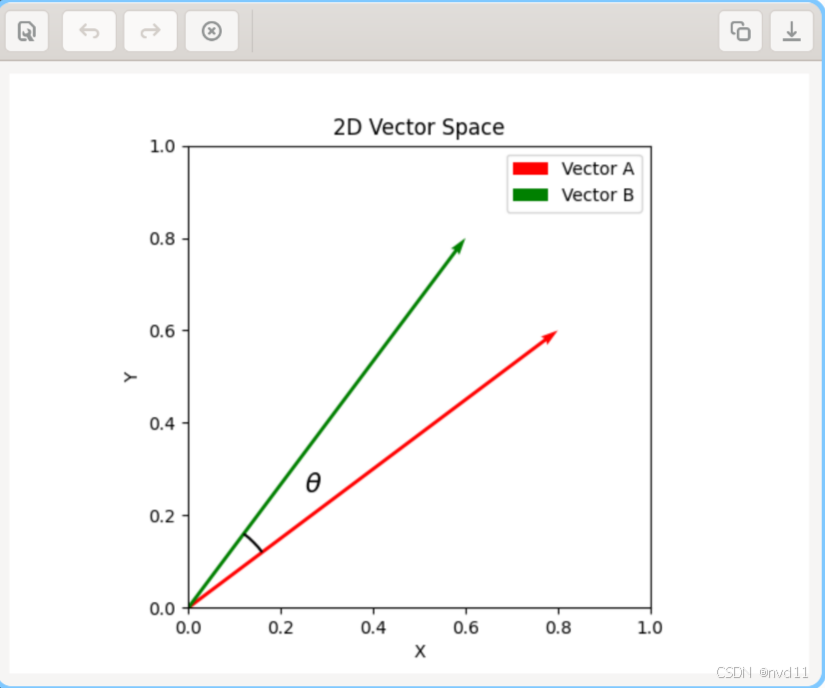
上图直观地展示了2维平面上的两个向量。余弦距离衡量的是这两个向量之间的夹角大小。夹角越小，两个向量方向越一致，余弦距离就越小，代表它们越相似。

3维空间中的余弦相似度

如果向量 A = (x1, y1, z1) 和 B = (x2, y2, z2)，则公式为：

cosine_similarity ( A , B ) = x 1 x 2 + y 1 y 2 + z 1 z 2 x 1 2 + y 1 2 + z 1 2 x 2 2 + y 2 2 + z 2 2 \text{cosine\_similarity}(A, B) = \frac{x_1 x_2 + y_1 y_2 + z_1 z_2}{\sqrt{x_1^2 + y_1^2 + z_1^2} \sqrt{x_2^2 + y_2^2 + z_2^2}} cosine_similarity(A,B)=x12+y12+z12 x22+y22+z22 x1x2+y1y2+z1z2

余弦距离 cosine_distance 则由余弦相似度派生而来：

cosine_distance ( A , B ) = 1 − cosine_similarity ( A , B ) \text{cosine\_distance}(A, B) = 1 - \text{cosine\_similarity}(A, B) cosine_distance(A,B)=1−cosine_similarity(A,B)

余弦距离的取值范围在 [0, 2] 之间。距离为0表示向量完全相同，距离越大表示向量差异越大。

RAG中余弦距离的应用

在RAG中，用户输入和知识库中的文档都被转换成了向量。为了找到最相关的文档，系统会计算用户输入向量与知识库中所有文档向量之间的余弦距离 cosine_distance，并选择距离最小的（即相似度最高的）文档。

这种方法的优点在于，它不受向量大小的影响，只关注向量的方向。这意味着，即使两段文本的长度相差很大，只要它们的主题或语义相似，它们的向量表示在方向上也会很接近，从而获得较高的余弦相似度。

为什么使用余弦距离而不是欧几里得距离？

在衡量向量相似度时，除了余弦距离，另一个常用的度量是欧几里得距离（Euclidean Distance），也就是空间中两点之间的直线距离。然而，在语义相似度的场景下，余弦距离通常是更好的选择。

关注方向而非大小: 欧几里得距离衡量的是向量终点之间的绝对距离，它会受到向量长度的影响。而余弦距离只关注向量之间的方向。在文本表示中，向量的长度通常与文档的长度（例如，词语的数量）有关。如果两篇文档讨论的是同一个主题，但一篇很长一篇很短，它们的向量表示在方向上可能很接近，但终点之间的距离可能很远。在这种情况下，余弦距离能够准确地捕捉到它们的语义相似性，而欧几里得距离则会因为长度的差异而产生误判。
高维空间中的稀疏性: 文本向量通常存在于非常高的维度空间中。在高维空间中，数据点之间的距离会变得非常稀疏，欧几里得距离的度量效果会下降。相比之下，余弦距离在高维空间中仍然能够有效地衡量方向上的差异。

总而言之，当我们关心的是内容的"主题"或"意义"（即方向）而不是文档的"长度"（即大小）时，余弦距离是更合适的度量方法。

pgvector如何加速高维向量搜索？

正如我们所讨论的，高维向量的余弦距离计算涉及大量的浮点运算。当数据库中有数百万甚至数十亿个向量时，逐一计算查询向量与每个数据库向量之间的距离（即"暴力"或"精确"搜索）是极其耗时且不可行的。为了解决这个问题，像pgvector这样的向量数据库采用了近似最近邻（Approximate Nearest Neighbor, ANN） 搜索技术。

ANN的核心思想是：牺牲一点点精度，来换取巨大的查询速度提升 。它不保证找到绝对最相似的top-k个结果，但在大多数情况下，它找到的结果与真实结果非常接近，足以满足应用需求。pgvector通过构建特殊的索引结构来实现ANN搜索。

1. IVFFlat (Inverted File Flat)

IVFFlat是一种基于聚类的索引方法。

构建过程:
1. 聚类 (Clustering) : 首先，pgvector会使用k-means算法将数据库中所有的向量分成k个簇（clusters）。每个簇都有一个中心点（centroid）。
2. 倒排文件 (Inverted File): 然后，它会创建一个"倒排文件"结构，其中每个簇的中心点都指向一个列表，这个列表包含了该簇中所有向量的ID。
查询过程:
1. 寻找中心点 : 当一个新的查询向量进来时，pgvector会先计算它与所有k个簇中心点的距离。
2. 缩小搜索范围 : 然后，它会选择与查询向量最接近的n个簇（n是一个可配置的参数，远小于k）。
3. 簇内搜索 : 最后，pgvector只在这n个被选中的簇内部进行精确的距离计算，从而找到top-k个最相似的向量。

通过这种方式，pgvector避免了对整个数据集进行扫描，而是将搜索范围缩小到了几个最有可能包含结果的簇中，从而大大提高了查询速度。

2. HNSW (Hierarchical Navigable Small World)

HNSW是一种基于图的索引方法，它在速度和精度方面通常比IVFFlat表现更优。

构建过程:
1. 分层图 (Layered Graph): HNSW会构建一个多层的图结构。最底层包含了所有的向量。往上每一层都是下一层的"高速公路"，包含的向量数量更少，节点之间的连接也更稀疏。
2. 远近连接 (Long & Short Links): 在每一层中，每个节点（向量）都会与其他一些节点建立连接。这些连接既包括距离较近的"邻居"，也包括一些距离较远的节点，以确保图的连通性。
查询过程:
1. 从顶层进入 : 查询从最顶层的"高速公路"开始。pgvector会在这里找到一个最接近查询向量的节点作为入口点。
2. 逐层下降: 然后，它会从这个入口点开始，在当前层中导航，不断寻找更接近查询向量的节点。当无法找到更近的节点时，它就会进入下一层。
3. 底层精确搜索 : 这个过程会一直持续到最底层。在最底层，pgvector会进行更精细的搜索，从而找到最终的top-k个结果。

HNSW通过这种从稀疏到稠密的图导航方式，能够非常快速地定位到查询向量所在的区域，从而实现极高的查询效率。

底层加速：SIMD指令集（如AVX512）

除了ANN索引算法之外，pgvector还在更底层的硬件层面进行了优化。现代CPU支持**单指令多数据流（Single Instruction, Multiple Data, SIMD）**指令集，例如AVX2和AVX512。

什么是SIMD?: SIMD允许CPU在一个指令周期内，同时对多个数据执行相同的操作。例如，一个常规的CPU指令一次只能计算两个浮点数的加法，而一条AVX512指令可以同时计算16个单精度浮点数的加法。
如何加速向量计算? : 向量的距离计算（无论是余弦距离还是欧几里得距离）都包含大量的重复性数学运算（如乘法、加法、开方）。这些运算非常适合使用SIMD指令进行并行处理。pgvector会自动检测CPU是否支持这些高级指令集，如果支持，就会利用它们来并行计算多个向量维度，从而将最核心的距离计算速度提升数倍。

因此，pgvector的快速响应能力是上层ANN算法 和底层硬件指令集优化相结合的结果。ANN算法减少了需要计算的向量数量，而SIMD指令则加快了每一次距离计算的速度。

3D坐标图可视化

为了更直观地理解向量和余弦距离，我们可以想象一个三维空间。在这个空间中，每个向量都可以被表示为一个从原点出发的箭头。两个向量之间的夹角越小，它们的余弦相似度就越高。

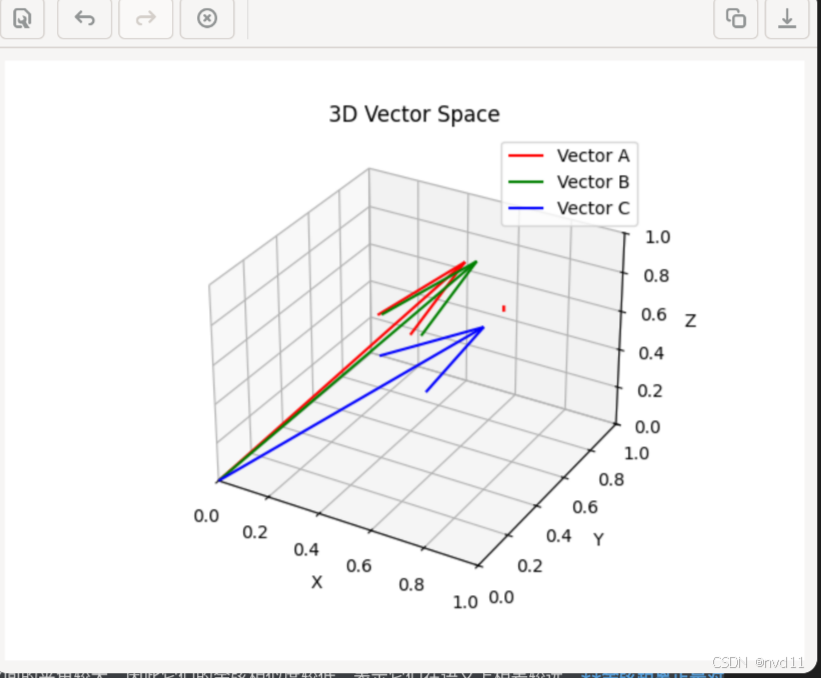
上图展示了三个向量 A 、B 和 C 。向量 A 和 B 之间的夹角很小，因此它们的余弦相似度很高，意味着它们在语义上是相关的。而向量 A 和 C 之间的夹角较大，因此它们的余弦相似度较低，表示它们在语义上相差较远。余弦距离正是对这个夹角大小的度量。

总结

RAG通过结合检索和生成，有效地提升了大型语言模型的性能。而向量余弦距离作为RAG核心的相似度度量方法，在从海量信息中精准地检索出相关内容方面发挥着关键作用。理解余弦距离的数学原理以及pgvector等工具如何通过ANN算法和底层SIMD指令优化来高效地实现向量搜索，有助于我们更深入地理解RAG以及其他基于向量嵌入的自然语言处理技术。