本章阅读顺序:
压缩映射定理(Contraction Mapping Theorem)
设 ( X , d ) (X, d) (X,d) 为非空的完备度量空间, ( T : X → X ) (T:X \to X) (T:X→X) 为 ( X ) (X) (X) 上的一个压缩映射 ,
即存在一个常数 q ∈ [ 0 , 1 ) q \in [0, 1) q∈[0,1),使得对任意 ( x , y ∈ X ) (x, y \in X) (x,y∈X),有
d ( T ( x ) , T ( y ) ) ≤ q ⋅ d ( x , y ) d(T(x), T(y)) \leq q \cdot d(x, y) d(T(x),T(y))≤q⋅d(x,y)
则映射 T T T 在 X X X 内存在唯一的 不动点 x ∗ x^{*} x∗, 即 T ( x ∗ ) = x ∗ T(x^{*}) = x^{*} T(x∗)=x∗。
此外,该不动点可通过如下迭代求得:
从任意 ( x 0 ∈ X ) (x_0 \in X) (x0∈X) 出发,定义迭代序列
x n = T ( x n − 1 ) , n = 1 , 2 , 3 , ... x_n = T(x_{n-1}), \quad n = 1, 2, 3, \dots xn=T(xn−1),n=1,2,3,...
则序列 { x n } \{x_n\} {xn} 收敛到 x ∗ x^{*} x∗,且满足以下误差估计:
d ( x ∗ , x n ) ≤ q n 1 − q d ( x 1 , x 0 ) . d(x^{*}, x_n) \leq \frac{q^n}{1 - q} \, d(x_1, x_0). d(x∗,xn)≤1−qqnd(x1,x0).
证明
在 MDP 中,状态价值函数 V(s) 满足 Bellman 方程(对于给定策略 π \pi π):
V π ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V π ( s ′ ) ] V^{\pi}(s) = \sum_{a} \pi(a|s) \sum_{s', r} p(s', r | s, a) \big[ r + \gamma V^{\pi}(s') \big] Vπ(s)=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γVπ(s′)]
- 定义 Bellman 算子 ( T π ) ( T^{\pi} ) (Tπ):
( T π V ) ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V ( s ′ ) ] (T^{\pi}V)(s) = \sum_{a} \pi(a|s) \sum_{s', r} p(s', r | s, a) \big[ r + \gamma V(s') \big] (TπV)(s)=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γV(s′)]
这是一个从价值函数空间到自身的算子。
设 ( V ) ( \mathcal{V} ) (V) 表示所有有界实值函数 V : S → R V: \mathcal{S} \to \mathbb{R} V:S→R 的集合,赋予无穷范数(sup 范数):
∥ V 1 − V 2 ∥ ∞ = max s ∈ S ∣ V 1 ( s ) − V 2 ( s ) ∣ \|V_1 - V_2\|\infty = \max{s \in \mathcal{S}} |V_1(s) - V_2(s)| ∥V1−V2∥∞=s∈Smax∣V1(s)−V2(s)∣
这个空间在无穷范数下是完备的(是一个 Banach 空间)。
对任意 ( V 1 , V 2 ∈ V ) ( V_1, V_2 \in \mathcal{V} ) (V1,V2∈V),计算:
∣ ( T π V 1 ) ( s ) − ( T π V 2 ) ( s ) ∣ = ∣ ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) γ [ V 1 ( s ′ ) − V 2 ( s ′ ) ] ∣ ≤ ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) γ ∣ V 1 ( s ′ ) − V 2 ( s ′ ) ∣ ≤ ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) γ ∥ V 1 − V 2 ∥ ∞ = γ ∥ V 1 − V 2 ∥ ∞ \begin{aligned} |(T^{\pi}V_1)(s) - (T^{\pi}V_2)(s)| &= \left| \sum_{a} \pi(a|s) \sum_{s', r} p(s', r|s,a) \gamma \big[ V_1(s') - V_2(s') \big] \right| \\ &\le \sum_{a} \pi(a|s) \sum_{s', r} p(s', r|s,a) \gamma \big| V_1(s') - V_2(s') \big| \\ &\le \sum_{a} \pi(a|s) \sum_{s', r} p(s', r|s,a) \gamma \| V_1 - V_2 \|\infty \\ &= \gamma \|V_1 - V_2\|\infty \end{aligned} ∣(TπV1)(s)−(TπV2)(s)∣= a∑π(a∣s)s′,r∑p(s′,r∣s,a)γ[V1(s′)−V2(s′)] ≤a∑π(a∣s)s′,r∑p(s′,r∣s,a)γ V1(s′)−V2(s′) ≤a∑π(a∣s)s′,r∑p(s′,r∣s,a)γ∥V1−V2∥∞=γ∥V1−V2∥∞
因为
∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) = 1 \sum_{a} \pi(a|s) \sum_{s', r} p(s', r|s,a) = 1 a∑π(a∣s)s′,r∑p(s′,r∣s,a)=1
于是:
max s ∣ ( T π V 1 ) ( s ) − ( T π V 2 ) ( s ) ∣ ≤ γ ∥ V 1 − V 2 ∥ ∞ \max_{s} |(T^\pi V_1)(s) - (T^\pi V_2)(s)| \le \gamma \| V_1 - V_2 \|_\infty smax∣(TπV1)(s)−(TπV2)(s)∣≤γ∥V1−V2∥∞
所以:
∥ T π V 1 − T π V 2 ∥ ∞ ≤ γ ∥ V 1 − V 2 ∥ ∞ \| T^\pi V_1 - T^\pi V_2 \|\infty \le \gamma \| V_1 - V_2 \|\infty ∥TπV1−TπV2∥∞≤γ∥V1−V2∥∞
Gridworld 示例
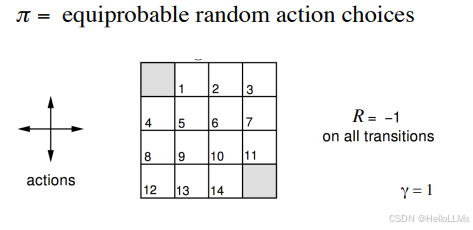
- 环境定义(MDP)
- 4 × 4 4\times 4 4×4 网格,共 16 个状态
- 终止状态:左上角 (1,1) 和右下角 (4,4)
- 非终止状态动作:上、下、左、右;若撞墙状态不变
- 奖励:每步 R = − 1 R=-1 R=−1
- 折扣因子: γ = 1 \gamma = 1 γ=1
- 策略:均匀随机策略 π ( a ∣ s ) = 1 4 \pi(a|s)=\frac{1}{4} π(a∣s)=41
- 更新过程

以第二行第二列为例:
- 当k = 1时
v 1 ( s ) = 1 4 ∑ a ∈ { 1 , 1 , ⋯ , − r } [ − 1 + v 0 ( s a ) ] v_1(s) = \frac{1}{4}\sum_{a\in\{1,1,\cdots,-r\}}\left[-1+v_0(s_a)\right] v1(s)=41a∈{1,1,⋯,−r}∑[−1+v0(sa)]
也就是 v 1 ( s ) = 1 4 ∗ [ ( − 1 ) + ( − 1 ) + ( − 1 ) + ( − 1 ) ] = − 1 v_1(s)=\frac{1}{4} * [(−1)+(−1)+(−1)+(−1)]=−1 v1(s)=41∗[(−1)+(−1)+(−1)+(−1)]=−1
- 当 k = 2时
v 2 ( s ) = 1 4 ∗ [ ( − 1 + 0 ) + ( − 1 − 1 ) + ( − 1 − 1 ) + ( − 1 − 1 ) ] = − 1.75 v_2(s)=\frac{1}{4} * [(−1 + 0)+(−1 - 1)+(−1 -1)+(−1 -1)]=−1.75 v2(s)=41∗[(−1+0)+(−1−1)+(−1−1)+(−1−1)]=−1.75实际上图后面的其他尾数被省略了