【AI-算法-01】ResNet (残差网络) & Skip Connections

ResNet (Deep Residual Learning) 是深度学习历史上的分水岭。

• 在 ResNet 之前：网络超过 20 层就很难训练（梯度消失/爆炸，退化问题）。

• 在 ResNet 之后：网络可以轻松堆叠到 100层、1000层。

更重要的是，Transformer (LLM 的基石) 里的核心机制之一就是 Residual Connection (残差连接)。不理解 ResNet，你就无法真正理解为什么现在的 GPT、Llama 能做得这么深而不崩溃。

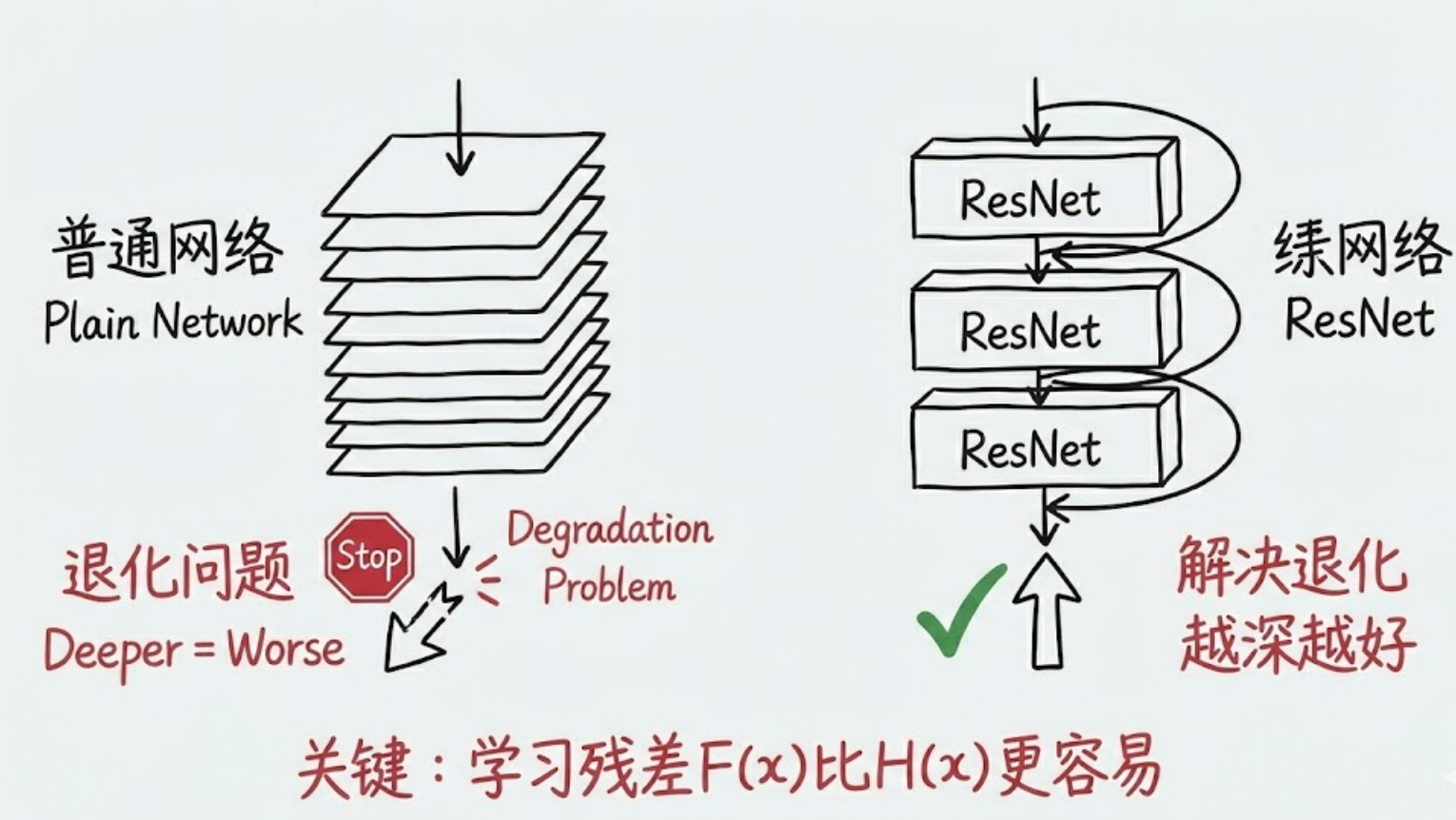
1. 为什么需要 ResNet？(The "Why")

在 ResNet 出现前，直觉告诉我们：网络越深，非线性表达能力越强，效果应该越好。但实验发现，当层数增加到一定程度，准确率反而下降 了。这不是 过拟合（训练误差也变高了），这被称为退化问题 (Degradation Problem)。

2. 核心思想：残差映射 (Residual Mapping)

ResNet 引入了 "Shortcut Connection"（捷径连接）。

假设我们想学习一个目标映射 。

• 传统网络 ：直接尝试学习。

• ResNet ：尝试学习残差函数。

  • 因此，原始映射变为：。

学习 "什么都不做"（即 F(x)=0，输出等于输入）比学习一个恒等映射（Identity Mapping）要容易得多。如果某一层是多余的，权重只需衰减到 0，网络就自动跳过了这一层。

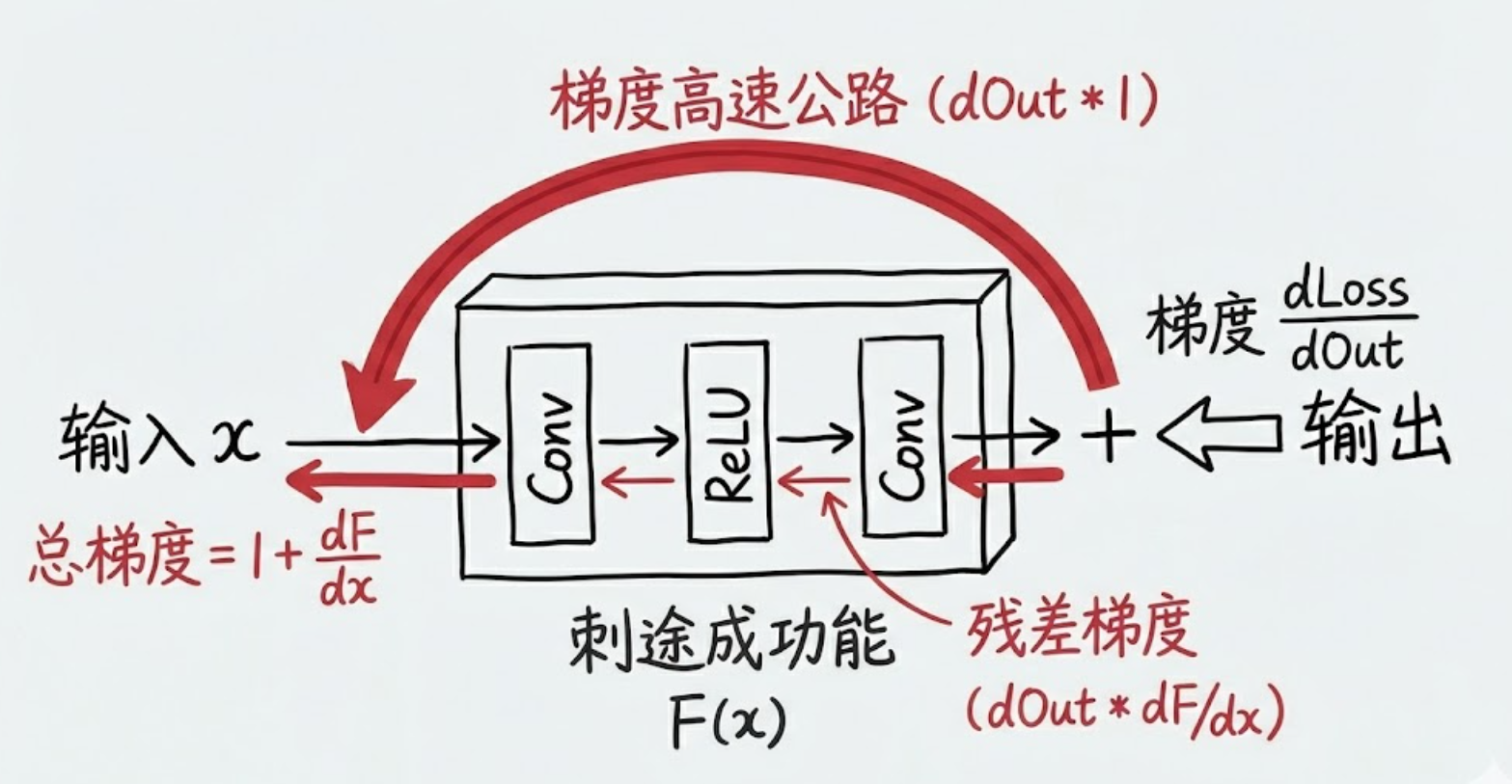
3. 数学推导：梯度高速公路 (Gradient Superhighway)

这是面试中最关键的推导。

假设一个残差块的公式为：

如果我们堆叠了 层（忽略激活函数，或者假设处于线性区），那么从第 层到第 层的关系是：

现在，我们需要根据损失函数 对 求梯度（反向传播）：

将 的公式代入：

3.1 拆解上面求导公式

第一行：链式法则展开

这里发生的事情是计算 。

回忆一下前向公式：。

对求导时：

1. 对自己求导 ：结果是 （这是单位矩阵 ）。

2. 对 求导 ：结果就是那一坨 。

第二行：分配律与物理意义 (The "Red Circle")

从第一行到第二行，其实就是做了一个简单的乘法分配律 展开：。

这一步为什么重要！

1. 传统的网络 (没有那个 "1")
   1. 如果是普通的串联网络（如 VGG），梯度是连乘的：
   2. 只要中间有一层的梯度小于 1（比如 0.9），连乘几十次后，。梯度就消失了。
2. ResNet 的魔法 (看公式第行)

   1. 因为有了公式里的 加法结构，总梯度被分成了两部分：

   2. 第一项 ， 这是**"保底梯度"**。

      1. 这一项不包含 任何权重 或激活函数的导数。这意味着，深层的梯度可以无损地、不经过任何衰减地直接"瞬移"回浅层。

      2. 这就是为什么 ResNet 即使堆到 1000 层，最前面的层依然能收到强有力的梯度信号。

   3. 第二项 ：这是**"修正梯度"**。

      • 它代表了梯度流经那些复杂的非线性层（卷积、ReLU）后产生的变化。

      • 关键点：即使这部分梯度因为梯度消失变成了 0，总梯度依然有第一项撑着！

3.2 这一项 有可能导致梯度爆炸（Explosion）吗?

是的，是有可能的。

虽然 '1' 解决了梯度消失，但后面那个连加项 如果每一层的导数都很大，加起来可能会导致总梯度变得非常大，导致梯度爆炸。

这也是为什么 ResNet 虽然解决了退化问题，但依然需要配合 BatchNorm 来约束每一层输出的分布，或者在初始化时把 的权重初始化得非常小（比如 Zero-init），让这一项在训练初期接近 0，从而使网络在开始时近似于恒等映射，保证稳定性。"

3.3 Batch Normalization (BN)

在 ResNet 的讨论中，我们提到了"梯度爆炸"的风险。Batch Normalization (BN) 就是那个把即将失控的数值强行按回地面的"镇压者"。

没有 BN，深度网络的每一层都在"由于前一层参数更新导致输入分布剧烈变化"的动荡中挣扎（这叫 Internal Covariate Shift）。每一层都得被迫去适应新的分布，训练就像在移动的跑步机上跑步。

BN 的核心作用就是：强行勒马 。无论前一层的输出变成了什么鬼样子（比如均值漂移到了 1000），BN 都会把它强行拉回到一个固定的分布（通常是均值 0，方差 1 附近）。

BN 是通过两个步骤来约束分布的："标准化 (Normalization)" 和 "再缩放 (Scale and Shift)"。

3.3.1 BN-标准化

Step 1: 暴力标准化 (The Constraint)

对于一个 Batch 的输入 （比如 shape 为 ），我们在通道 (Channel) 维度上计算均值和方差。

对于第 个通道：

1. 计算均值 ：

2. 计算方差 ：

3. 归一化：

   

这一步是硬约束。无论 原来是多少，经过这一步，数据被 "标准化 (Standardization)" 或者 "Z-Score 归一化"。

它能保证的是：无论输入 是什么分布（正态、均匀、双峰...），经过变换后的 一定满足均值为 0，方差为 1 。至于形状是不是钟形曲线（正态），取决于输入 长什么样，BN 不会改变数据的"形状"。

• 好处：梯度流更加稳定，不会因为数值过大导致梯度爆炸，也不会因为数值过小导致梯度消失（特别是在 Sigmoid/Tanh 时代）。

3.3.2 BN-缩放

如果仅仅强制为 ，可能会破坏网络学到的特征（比如某个特征本身就应该是正数，强制变成 0 均值就切断了一半信息）。所以 BN 引入了两个可学习参数 (缩放) 和 (平移)：

物理含义：

• ：允许网络恢复方差。

• ：允许网络恢复均值。

• 如果网络发现保持原始分布最好，它可以学习成 , （即变回去了）。但在实践中，网络通常会学到一个有利于下一层（比如 ReLU）激活的分布。

4. 为什么 Transformer (LLM) 不用 BN？

这是一个架构演进的关键点。

• ResNet (CNN) 使用 BN：

  • CNN 处理的是图像，同一 Batch 内不同样本的同一通道（例如"边缘检测"通道）具有相似的统计特性。BN 在 Batch 维度归一化是合理的。

• Transformer (NLP) 使用 Layer Normalization (LN)：

  • NLP 序列长度不一，且 Batch 内句子差异巨大。计算 Batch 均值往往没有意义。

  • LN 是对每一个样本自己的所有通道（Embedding 维度）做归一化，不依赖 Batch Size。

融合加速 (Conv-BN Fusion)

在模型部署（TensorRT / ONNX）时，BN 层通常会被"吸"进前面的卷积层里。

因为：

这是一个纯线性变换。我们可以把 全部融合进卷积核的权重 和偏置 中。

这样推理时就没有 BN 层了，速度更快。

5. Questions

"大家都知道 ResNet 解决了梯度消失问题。但是，有研究表明 ResNet 实际上表现得像浅层网络的集成（Ensemble of Shallow Networks）。请解释这个观点，并从这个角度说明为什么删除 ResNet 中的某一层不会像删除 VGG 中的某一层那样导致网络瘫痪？

展开公式： 对于一个 3 层的 ResNet，，展开后其实包含 条路径：7

• 路径 1: (全跳过)

• 路径 2:

• 路径 3:

• ...

• 路径 N: (最长路径)

**二项式分布：**ResNet 的梯度主要通过那些较短的路径传播。这就像是把许多不同深度的浅层网络并联在一起。

鲁棒性对比：

• VGG (串联系统) ：。删掉 ，数据流断裂，网络直接瘫痪。

• ResNet (并联系统) ：删掉 ，只是去掉了经过 的那些路径。由于还存在 或 等大量其他路径，网络性能只会平滑下降，而不会崩溃