射频网课学习第四章(稳定性分析)

第一部分：稳定性问题的物理本质与数学描述

1.1 引言

在上一章我们了解了晶体管的核心指标------增益，而这一章我们了解晶体管稳定性，或者说放大器的"稳定度"问题。只有先让放大器能够稳定的输出，我们才能谈所谓的增益，不然增益无穷大，但一点用都没有，我们根本用不了。

1.2 谐振与振荡

我们首先要厘清两个关键概念：什么是 谐振条件(resonant) ，以及什么是 振荡(oscillation)。

这里有一个常见的中文翻译误区：很多人把"Resonance"翻译成"振荡"，这是不准确的。

Resonance 的正确中文翻译应该是 "共振" 或 "谐振"。
Oscillation 才是我们所说的 "振荡"。

那么，如何区分"共振"和"振荡"呢？

1. 什么是"共振"？

想象一个 LC谐振腔（比如一个电感L和一个电容C组成的电路）。这个谐振腔有一个特定的"谐振频率"。

在这个特定频率下，会出现以下情况：

如果电路是并联结构，那么所有元件的导纳相加会等于零。
如果电路是串联结构，那么所有元件的阻抗相加会等于零。

这都属于"共振"现象。

当共振发生时，会发生什么奇妙的事情呢？

以并联LC电路为例：在谐振频率下，你不需要从外部给这个谐振腔注入电流，它的两端自己就会产生一个电压。这意味着从外部看进去的阻抗是无限大的。

电路内部的能量（在电感和电容之间）自己来回交换、往复流动，不需要外界提供能量来维持。就像一个压电晶体：在其谐振频率上，你甚至不需要给它电压，它内部的晶体结构自己就会因为机械特性而振动。这就是它的"谐振频率"。

所以，这种自身存在能量交换、不需要外部能量维持 的状态，就是 "共振" 。这个LC电路或压电晶体，我们称之为 "共振子" 或 "谐振腔"，它是构成振荡器的基础元件。

理想情况下，如果一个共振腔内部没有任何电阻损耗，那么一旦给它一个初始能量（比如充一下电），内部的电流就会永无止境地在L和C之间来回流动，电压也会持续摆动，幅度永不衰减。

但实际上，现实中不存在完全没有损耗的共振腔（超导体可能接近），所以能量总会慢慢被消耗掉。

2. 什么是"振荡"？
振荡则是指一个信号幅度持续增长的过程。一个电路要产生振荡，输出信号必须有越来越大的趋势。

那么，信号变大的能量从哪里来？天下没有免费的午餐------必须有一个主动元件 （如晶体管 或二极管）提供一个直流电源，并将能量转换成不断增长的交流信号。

最终，这个增长的信号不会无限大下去，因为晶体管会进入饱和或截止区，从而将电压幅度限制在一个稳定值。所以，振荡的典型过程是：起振时幅度越来越大，最终达到一个稳定的振荡状态。

总结一下核心区别：

共振：一个被动的能量交换状态，理想下幅度不变。
振荡：一个主动的能量增长过程，需要直流电源供电，起振时幅度增大。

振荡器的工作原理

一个振荡器就是由一个被动的共振子 ，配合一个主动的电路（晶体管）构成的。晶体管的作用就是提供能量，让信号产生并增长起来。

振荡的数学条件

当我们设计放大器时，必须千方百计避免满足振荡条件，否则你的放大器就会意外地变成一个振荡器！

分析方法很简单：在电路的任意一个点把它"切开"成两半。

向左看，阻抗是ZAZ_AZA，相对于50欧姆的反射系数是ΓAΓ_AΓA。
向右看，阻抗是ZBZ_BZB，相对于50欧姆的反射系数是ΓBΓ_BΓB。

谐振条件 是：ΓA×ΓB=1Γ_A × Γ_B = 1ΓA×ΓB=1。

这个等式包含了两个至关重要的条件，缺一不可：

幅度条件 ：∣ΓA×ΓB∣=1|Γ_A × Γ_B| = 1∣ΓA×ΓB∣=1。这意味着信号环绕一圈回来的"增益"正好是1。
相位条件 ：∠(ΓA×ΓB)=0°∠(Γ_A × Γ_B) = 0°∠(ΓA×ΓB)=0°。这意味着信号环绕一圈回来的相位必须是零度（即360度的整数倍）。

为什么需要这两个条件？

想象信号从切面出发，经过右边反射，再经过左边反射，最后回到原点。如果相位是0度，那么新回来的信号会和原始信号建设性地叠加 （同相相加）。如果这一圈的增益又正好是1，那么信号就能维持不变，形成共振。

如何让电路"起振"？

要让电路从无到有地建立起振荡，我们需要更激进的条件：

相位条件 依然必须满足（相位差为0°）。
幅度条件 需要更强：∣ΓA×ΓB∣>1|Γ_A × Γ_B| > 1∣ΓA×ΓB∣>1。

这意味着信号每环绕一圈，幅度不仅没衰减，反而被放大了（比如增益是1.1）。这样一圈、两圈、三圈下来，信号就会像滚雪球一样越来越大 ，形成我们想要的振荡。

在实际设计中，这通常意味着电路某部分要呈现出 "负电阻" 的特性。当负电阻足够大，足以抵消电路中的正电阻损耗时，就能满足 ∣ΓA×ΓB∣>1|Γ_A × Γ_B| > 1∣ΓA×ΓB∣>1的条件，从而成功地让振荡器起振。

1.3 二端口网络稳定性

好的，我们继续。接下来，根据前面讨论的振荡条件，我们要具体分析一个二端口网络------也就是晶体管本身的稳定性。

晶体管有其S参数，构成了一个二端口网络。在这个网络分析中，我们会关注四个反射系数：ΓS,ΓIN,ΓL,ΓOUTΓ_S, Γ_{IN}, Γ_L, Γ_{OUT}ΓS,ΓIN,ΓL,ΓOUT。

当我们实际设计电路时，这个框图里究竟包含了哪些部分？

好，不要忘记。ΓSΓ_SΓS（源反射系数）包含了50欧姆的信号源 以及输入端的匹配电路 。所以，从晶体管输入端看向信号源，所看到的阻抗对应的反射系数就是我们的ΓSΓ_SΓS。同理，ΓLΓ_LΓL（负载反射系数）包含了什么？它包含了输出端的匹配电路 以及50欧姆的负载 。很多人会忘记这一点！请记住，ΓLΓ_LΓL是从晶体管输出端看出去，一直看到50欧姆负载，这两部分合起来所对应的反射系数。

那么， ΓINΓ_{IN}ΓIN又包含了什么呢？它是从晶体管前端看进去的阻抗，但晶体管会一直"看"到后端，信号会弹回来。所以，ΓINΓ_{IN}ΓIN实际上包含了晶体管本身 、输出端匹配电路 以及50欧姆负载 的影响。

最后复习一下ΓOUTΓ_{OUT}ΓOUT，它包含了什么？它包含了晶体管本身 、输入端匹配电路 以及50欧姆信号源 。因为你从晶体管后端看进去，会看到前端的ΓINΓ_{IN}ΓIN以及输入端的50欧姆，这些合起来决定了ΓOUTΓ_{OUT}ΓOUT。

我们将利用这四个参数来判断我们的电路是否满足振荡条件、是否会起振，或者说，判断它到底是稳定的还是不稳定的。

首先，我们介绍两个核心概念。

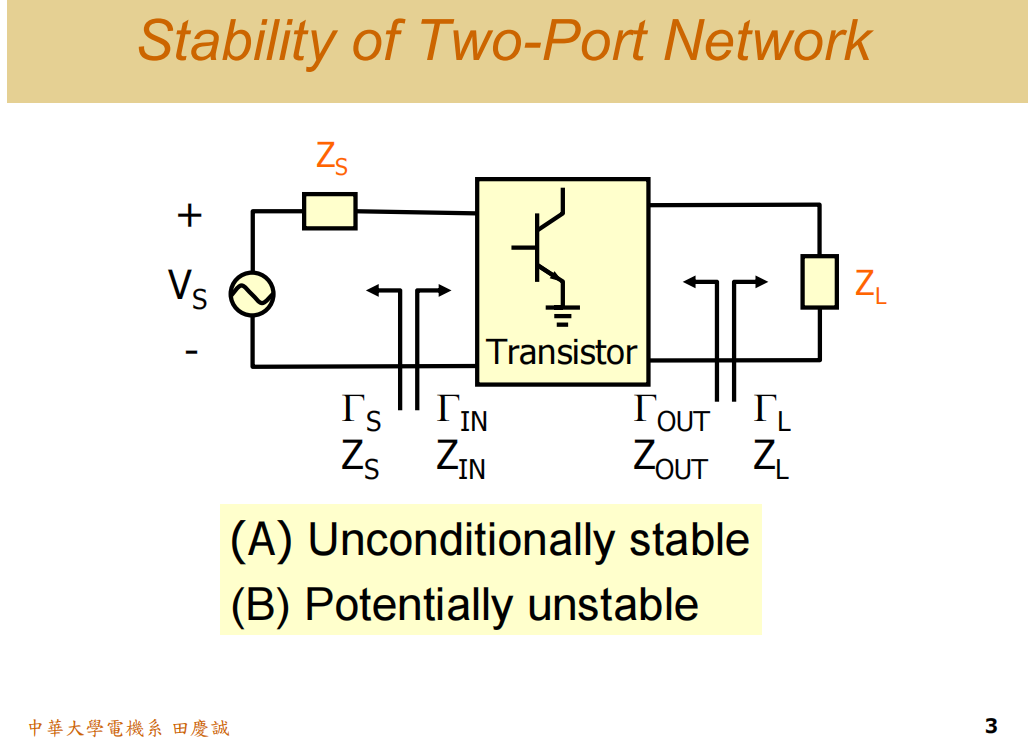
第一个是 "无条件稳定(Unconditionally stable)" 。

什么是"无条件稳定"？

一句话概括就是：无论你如何选择源和负载的匹配网络（只要是被动元件），放大器都保证不会振荡。

既然是你来设计，是不是可以任意选择ΓSΓ_SΓS和ΓLΓ_LΓL？
ΓSΓ_SΓS应该用什么来表示？它应该落在一个史密斯圆图上，其模值|ΓSΓ_SΓS| < 1。这个圆图我们称之为ΓSΓ_SΓS平面。

我在ΓSΓ_SΓS平面上任意取一点，代表什么物理意义？代表你已经完成了输入匹配电路的设计 ！你选择了一个ΓSΓ_SΓS，就意味着你用被动的电感和电容完成了输入匹配。里面没有晶体管，没有负电阻，没有二极管，没有非线性电路。所以，它的反射系数绝对值绝对不会大于1 。因此，这个圆内的任何一点，都代表你的输入匹配已经做完了。

同样，ΓLΓ_LΓL平面也是如此，你任意选一个ΓLΓ_LΓL，也代表输出匹配做完了，并且|ΓLΓ_LΓL| ≤ 1。因为你用的都是被动的电感、电容、电阻或传输线，反射系数不可能大于1。

那么，"无条件稳定"的意思就是：我让你在这两个圆内随便选！无论选哪一点，我的晶体管电路都保证不会发生振荡。这就叫无条件稳定。

那什么又是 "潜在不稳定(Potentially unstable)" 呢？

它的意思是：抱歉，有些区域你不能选 。比如在ΓSΓ_SΓS平面上，有一块区域，如果你不小心选到了这一点，并把匹配电路做成这样，那就要小心了，晶体管可能会振荡。这个区域就叫不稳定区。换句话说，有部分的ΓSΓ_SΓS值不能取。另一个例子，在ΓLΓ_LΓL平面上也可能有一块区域不能取，取到之后，整个电路可能会不稳定。这种有部分区域需要规避的情况，我们就称之为"潜在不稳定"。

接下来我们看数学上的定义。

同样我们先讲"无条件稳定"。

匹配网络都是用LC或者传输线做出来的被动电路。被动电路是不可能让反射系数大于1的。所以我们能选的，就是史密斯圆图单位圆内部的区域。

那么，为什么无条件稳定的定义是 |ΓINΓ_{IN}ΓIN| < 1 并且 |ΓOUTΓ_{OUT}ΓOUT| < 1 呢？

原因就在于我们需要避开产生振荡的可能性 。振荡的幅度条件是什么？在任何一个界面切开来，如果|ΓA×ΓBΓ_A × Γ_BΓA×ΓB| ≥ 1，那就有可能振荡了，对晶体管来说就可能振荡了（当然还有相位条件，但至少幅度条件满足了，就存在潜在风险）。

那我们来看，这四个参数，谁和谁配对？

在晶体管的前端界面切开：
- 往左看是 ΓSΓ_SΓS
- 往右看是ΓINΓ_{IN}ΓIN
- 它们俩是配对的。因为|ΓSΓ_SΓS| < 1 且 |ΓINΓ_{IN}ΓIN| < 1，所以有|ΓSΓ_SΓS × ΓINΓ_{IN}ΓIN| < 1。这个界面保证稳定，没问题。
在晶体管的后端界面切开：
- 往左看是 ΓOUTΓ_{OUT}ΓOUT
- 往右看是 ΓLΓ_LΓL
- 它们俩是配对的。因为|ΓOUTΓ_{OUT}ΓOUT| < 1 且 |ΓLΓ_LΓL| < 1，所以 |ΓOUTΓ_{OUT}ΓOUT × ΓLΓ_LΓL| < 1。这个界面也保证稳定。

因此，前后两个界面都保证不会起振，那么整个电路也保证不会起振。通常，|ΓSΓ_SΓS|<1和|ΓLΓ_LΓL|<1不算是"条件"，而是使用被动元件构造匹配网络时的"已知前提" 。

所以，满足 |ΓINΓ_{IN}ΓIN|<1 和 ΓOUTΓ_{OUT}ΓOUT|<1 这两个真正的稳定条件，就是无条件稳定。

理解了这一点后，我们再深入一下。

ΓINΓ_{IN}ΓIN是谁的函数？是和 ΓLΓ_LΓL 有关的。如果 |ΓINΓ_{IN}ΓIN| > 1，代表哪一级不稳定？是前级（输入）不稳定，对吧？

那么前级不稳定是谁造成的？是谁的"罪过"？是ΓSΓ_SΓS吗？不，是ΓLΓ_LΓL。罪魁祸首其实是后级（负载） ！前级不稳定可能是后级匹配没选好 。你后级ΓLΓ_LΓL乱选，有可能导致 |ΓINΓ_{IN}ΓIN| > 1。当然，晶体管本身的S11S_{11}S11也有作用，但后级的影响非常关键。

同理，如果 |ΓOUTΓ_{OUT}ΓOUT| > 1，是谁不稳定？是后级输出不稳定。后级不稳定，除了晶体管本身的S22S_{22}S22影响，还有谁的影响最大？是你前级的ΓS没有选好！你前级的匹配电路没选好，会造成你后级可能不稳定。

所以，总结一下这个重要关系：

前级不稳定，可能是后级匹配影响的。
后级不稳定，可能是前级匹配造成的。

从阻抗的角度看，这等价于 ZINZ_{IN}ZIN 的实部要大于0（正电阻），其反射系数的模值就会小于1。同理，如果 ZOUTZ_{OUT}ZOUT 的实部大于0，ΓOUTΓ_{OUT}ΓOUT 的模值就会小于1。这两个表述是完全等价的。核心就是看进去的阻抗不能有负电阻！

再来讲"潜在不稳定"。

刚才讲的是绝对稳定，现在是可能不稳定。注意，我只是说"可能"，没有说它一定会振荡。为什么？因为相位条件满不满足还不知道 。而且光 |ΓINΓ_{IN}ΓIN| > 1，也不能保证 |ΓSΓ_SΓS × ΓINΓ_{IN}ΓIN| 一定会大于1.
ΓSΓ_SΓS也是我们随便选的，所以，连幅度条件都只是"有可能"成立。我只能说"有可能"不稳定。

因此，我们说"潜在"的意思就是只有可能性。至于会不会真的振荡，我们并不知道。

但是，在业界工作的时候，只要有可能造成公司亏损，你会去冒险吗？你会去赌吗？你大概不会，老板也绝对不会去赌！所以，只要有可能会不稳定，你这个放大器的设计，老板绝对不敢要。他一定会要求你设计成无条件稳定的放大器，绝对不可能接受一个有可能不稳定的设计。这是不可以接受的。

所以，结论是：

如果你发现 |ΓINΓ_{IN}ΓIN| > 1，或者 |ΓOUTΓ_{OUT}ΓOUT| > 1，这两个情况都有可能 带来不稳定。我在这里要强调一下，这只是有可能 产生 |ΓA×ΓBΓ_A × Γ_BΓA×ΓB| = 1 的情况。

而当这个乘积确实等于1，并且同时满足相位条件时，振荡条件就正式成立，你的放大器马上就变成了一个标准的振荡器。

因此，用S参数来判断振荡器的标准条件，就是要去检测是否同时满足了幅度和相位的谐振条件。如果都满足，那这就是一个确定会起振的振荡器。

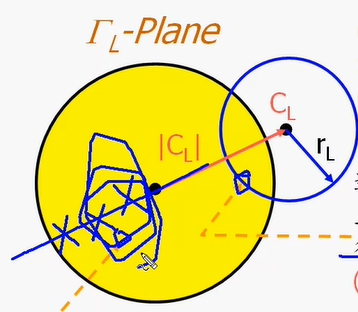
1.4 输出稳定圆与输入稳定圆

根据刚才的数学推导，我们来定义所谓的"输出稳定圆"。

输出稳定圆(output stability circles)

这个圆是画在 ΓLΓ_LΓL 平面 上的。ΓLΓ_LΓL 是你的选择，它一定会落在这个平面上半径小于1的单位圆内。你在这个圆上选一点，就代表你完成了一个输出匹配电路。

现在，我们根据 |ΓINΓ_{IN}ΓIN| = 1 这个条件，可以在 ΓLΓ_LΓL 平面上画出一个圆。这个圆有圆心和半径，它的方程式就是 |ΓINΓ_{IN}ΓIN| = 1。这个圆就叫做 输出稳定圆。

假设我们画出来的输出稳定圆长这样。

我要问一个问题：这个圆是基于 |ΓINΓ_{IN}ΓIN| = 1 画的。那么，输出稳定圆代表的是前级不稳定还是后级不稳定？

很多人想都不想："Output？那肯定是后级不稳定嘛！" 错了！恰恰相反。|ΓINΓ_{IN}ΓIN| = 1 是谁不稳定？是前级输入不稳定！

那为什么它要叫"输出稳定圆"呢？因为它是在 ΓLΓ_LΓL 平面 上画的。ΓLΓ_LΓL 是和什么相关的？是你在做输出匹配 时要选择的。在做输出匹配时，你需要考虑稳定度问题，所以你要参考这个圈圈。因为你输出端（ΓLΓ_LΓL）如果乱选 ，可能会导致输入端（Input）不稳定。

所以，这个圈圈是用来指导你如何选择 ΓLΓ_LΓL才能得到一个稳定的范围。举个例子，可能圈圈内部是不稳定区域，外部是稳定区域。我们把这个圈圈称为输出稳定圆，但它的物理意义是：警告你如果ΓLΓ_LΓL选在禁区内，会导致前级不稳定。

这个圆的圆心和半径都可以从S参数直接计算出来。很简单，只要给我S参数，我就能把这个圆画出来。这个公式需要背吗？完全不需要。因为所有软件都会帮你算。

输出稳定圆的物理意义与应用

在 ΓLΓ_LΓL平面上随便选一点，物理意义是什么？代表你完成了一个输出匹配网络。

那么，如果你不小心把 ΓLΓ_LΓL 选到了这个输出稳定圆上面，会发生什么事？这代表你完成这个输出匹配后，糟糕了，你的 ΓINΓ_{IN}ΓIN的模值等于 1 ，输入端可能会变得不稳定。

预告一下：后面我们教放大器设计，比如设计最大增益放大器时，如果你把工作点选到这里，你的增益会变成多少？无限大 ！保证会起振，你做的功率放大器就直接变成标准振荡器了。

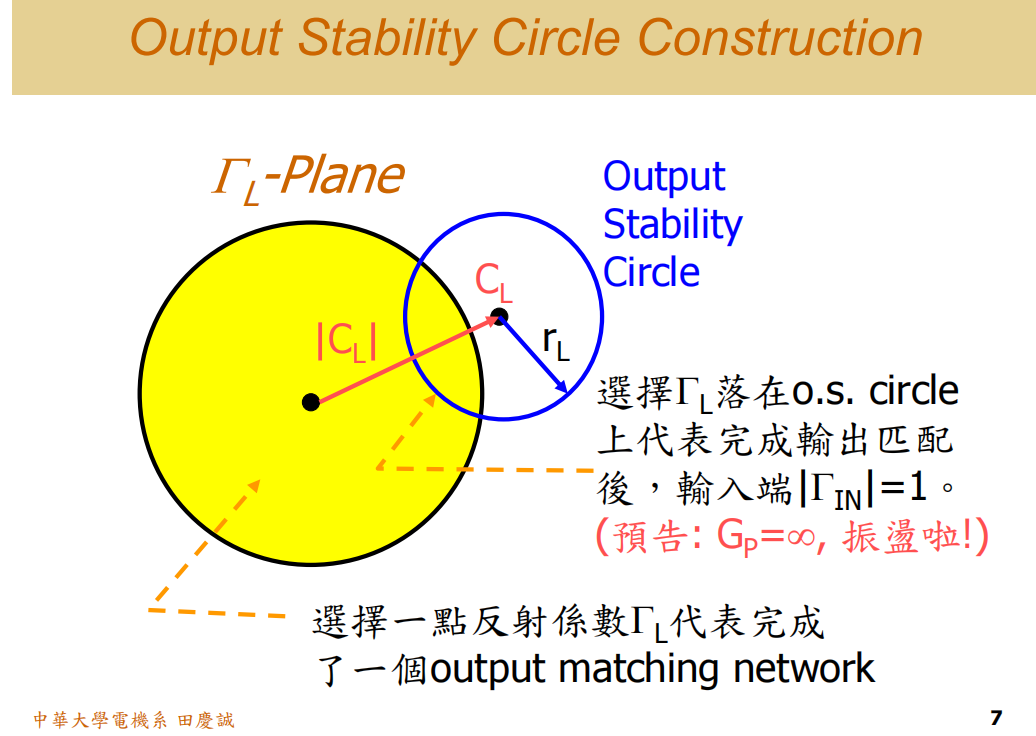
所以，各位同学，现在有感觉了吗？请问，我的稳定圆在这里，你的 ΓLΓ_LΓL选哪一点比较合适？如果是你，你会选哪里？

是这里吗？对，离它远一点 比较好。你离它越远，稳定性就越好。也就是说，哪个点离稳定圆最远？通常是往这个方向（圆心反方向）。选在这个区域就比较稳妥。

你选太偏边上好不好？也不好，那样匹配电路的Q值太高，带宽窄，也不是好选择。所以大概在圆心反方向的这个区域，是比较好的选择。这样你的电路就比较不容易产生振荡。

工程实践中的深层考量

那么问题来了：比如我选这个点（指一个离稳定圆很近但仍在稳定区内的点）。哎，老师，我这里也是稳定的啊！我这里也很稳啊！为什么我一定要选离它远一点的那个点呢？为什么我这个点就不行？

这就好比职场新人和老板的对话。六七年级的新人很喜欢说："老板，这很好啊，这有什么不好？" 心直口快，这可能是你们的写照。但老板的火气可能马上就上来了。然后你还不懂："老板你为什么要发火？理论告诉我这里很好啊！"

你觉得老板会给你什么答案？老板可能会说："好，你要尊重是吧？产品有任何问题，你负不负责？" 听到这话，你大概就怂了："老板，我选那个点（离得远的）就是了。"

事后你再去问老板为什么。五年级的老板从小被三四年级的欺负到大，他们超级会保护自己，做事非常严谨，绝对会再三考虑，不允许出任何纰漏。

我来问你：你设计放大器的时候，前后级接的是什么？都是理想的50欧姆，对吧？你设计好了，这点（离稳定圆近的点）确实在稳定区。但等你真正做完，去接别人的电路时，别人的电路还是理想的50欧姆吗？怎么可能！你这个点在实际应用中还会乖乖待在这里吗？才不会！它可能"嗖"一下就跑到不稳定区里面去了。然后整批货都不用出了。

再比如，你从台湾做好卖到美国，温度降到零下40度，这个点"啾"一下又跑进去了，你怎么知道是为什么？所以问题太多了，你不能考虑得那么简单。

还有，你在实验室做原型机，做了5颗，5颗都能用。一到生产线量产，良率"啪"掉到60%。老板问你："你不是说5颗都能用吗？怎么良率只剩60%？" 一查，糟糕。元器件没有误差吗？随便也有5%的误差。你的匹配点不小心就跑到不稳定区里了。

种种因素告诉你，如果能避开，就一定要想清楚前因后果。最稳妥的方法才是最好的。所以选离稳定圆远的地方，就算有误差、温度变化、人为因素，它跳进不稳定区的概率也是最低的。

所以，在做设计时要考虑到各种现实因素。到了业界，不要只跟老板说"我老师以前说理论上这样可行"。理论和实际之间还隔着无数"天灾人祸"。在做学问的时候就要考虑得更周全一点，这样才能和你的老板有效沟通。在"班门弄斧"之前要想清楚，老板的经验绝对比你老练。

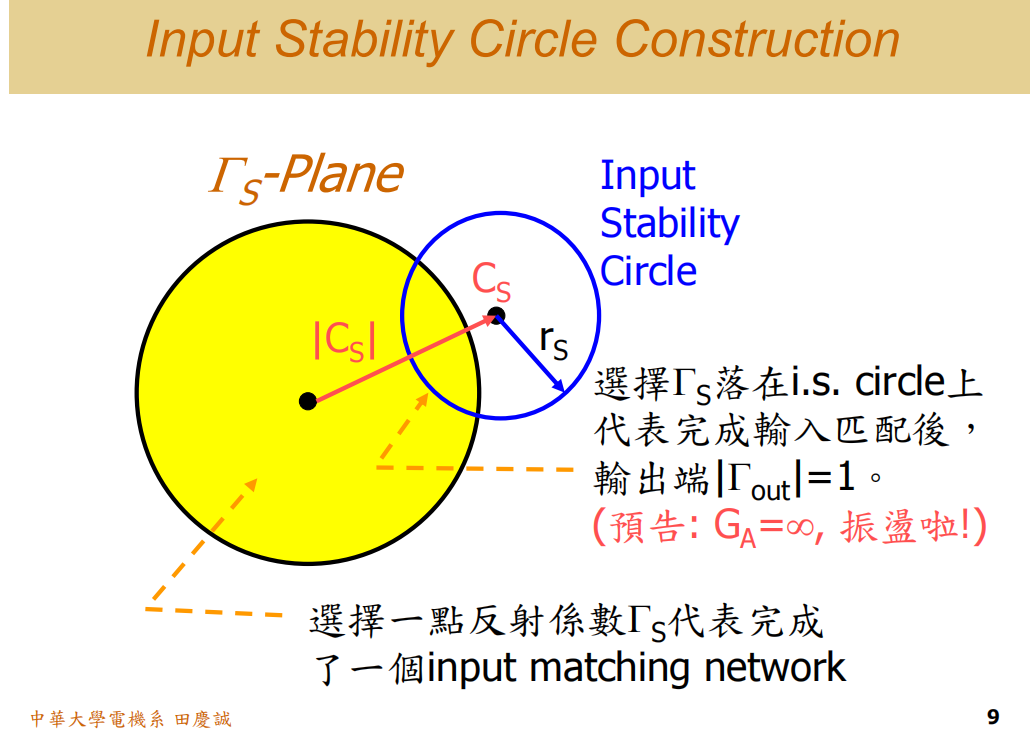
输入稳定圆(Input Stability Circles)

接下来是输入稳定圆，这个就没什么问题了。

输入稳定圆定义在 ΓSΓ_SΓS平面 上。它规范的是我的 ΓSΓ_SΓS 应该如何选择。同样，要记住它的物理意义：如果你的 ΓSΓ_SΓS选在了这个输入稳定圆上，代表什么？那你的 ΓOUTΓ_{OUT}ΓOUT 的模值会等于 1 ，输出端会变得不稳定 。所以这个圈圈是在警告你：你做的输入匹配 ，可能会导致输出不稳定。

同样，圆心半径公式都给你，看结果就行。

我们再复习一遍。未来你们用软件模拟，看到它画出的稳定圆，第一件事就是要判断：这个圆是在哪个平面？是 ΓSΓ_SΓS平面还是 ΓLΓ_LΓL平面？软件通常不会直接告诉你，你需要自己判断。

在ΓSΓ_SΓS平面上取一点代表什么？代表你完成了一个输入匹配网络 。如果你设计完输入匹配，发现工作点落在这个输入稳定圆上（或圆内不稳定区），那就代表：很抱歉，你的输出端开始不稳定了。

预告一下，如果我们设计低噪声放大器 ，一般就是做最小噪声系数设计。它唯一的变量就是前级的ΓSΓ_SΓS。你为了得到最低的噪声，结果选到了这个点上。"我的噪声好低啊！" 结果呢？电路变成了一个振荡器，一个"低噪声振荡器"！太棒了！本来是做低噪声放大器，结果成了低噪声振荡器。如果你选择在这一点，对于可用功率增益来说，它绝对是无限大的。

所以，你在选择ΓSΓ_SΓS的时候，也请你离开输入稳定圆越远越好 。同样，在这个区域（指向图示中离输入稳定圆较远的区域）可能是比较好的选择，会更稳定一些。

1.5 判断稳定区域

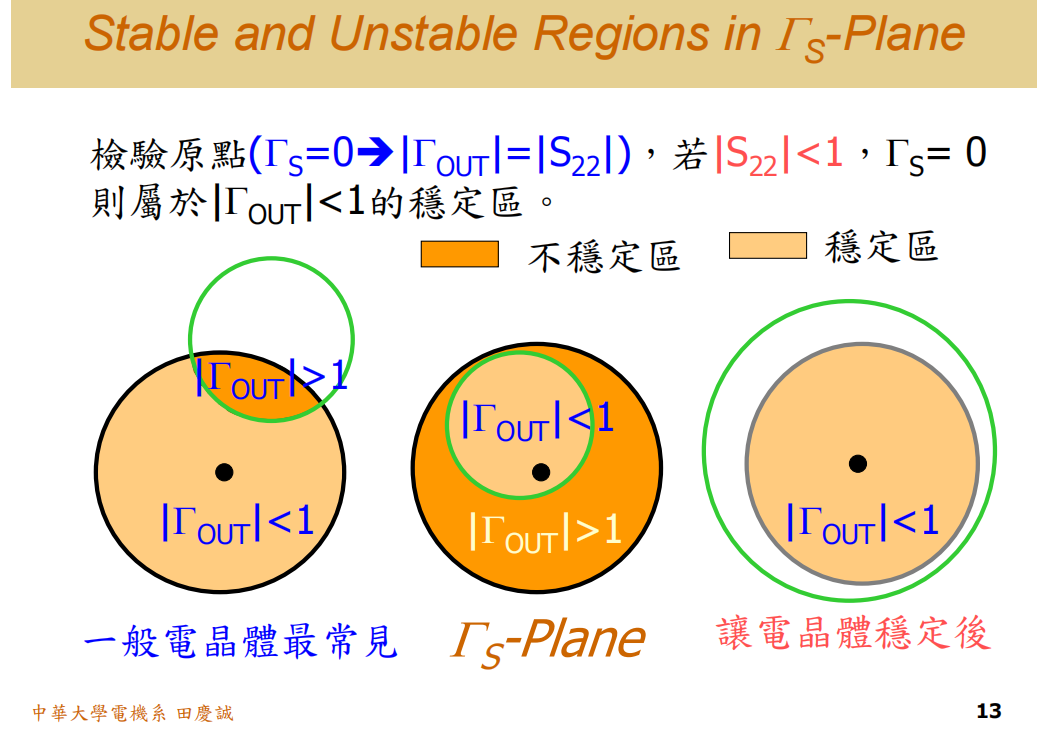
这个圈圈有分里面和外面，那到底是里面稳定还是外面稳定呢？

接下来我们就来学习一个判断的方法。

首先，我们要记得在 ΓLΓ_LΓL平面上画出来的圈圈是什么？

是 Output Stability Circle（输出稳定圆）

那么，我们要如何判断这个圈圈的内部和外部，哪一边是稳定的呢？

其实我们只需要判断一个点------原点，只要看这一点就够了，其他部分暂时不用管。

好，我们来看原点。选择这一点有什么物理意义呢？我这样做代表了什么？是做了 Input Matching（输入匹配）还是 Output Matching（输出匹配）呢？

我选择了 ΓLΓ_LΓL 平面上的一点，这一点是ΓLΓ_LΓL = 0。
ΓLΓ_LΓL = 0 代表什么？
代表我不需要做任何输出匹配电路，直接接上 50 欧姆负载就可以了 。也就是说，我把输出端直接接上 50 欧姆，就对应到这一点。

那么，当 ΓLΓ_LΓL = 0 时，ΓINΓ_{IN}ΓIN等于多少呢？

代入公式，剩下的就是 S11S₁₁S11，也就是说 ΓIN=S11Γ_{IN} = S₁₁ΓIN=S11。

那这时候就会有两种情况，第一种情况是S11S₁₁S11大于1，第二种情况是S11S₁₁S11小于1

我们先来看第一种情况，假设晶体管的S11S₁₁S11大于 1，那这代表什么意义呢？

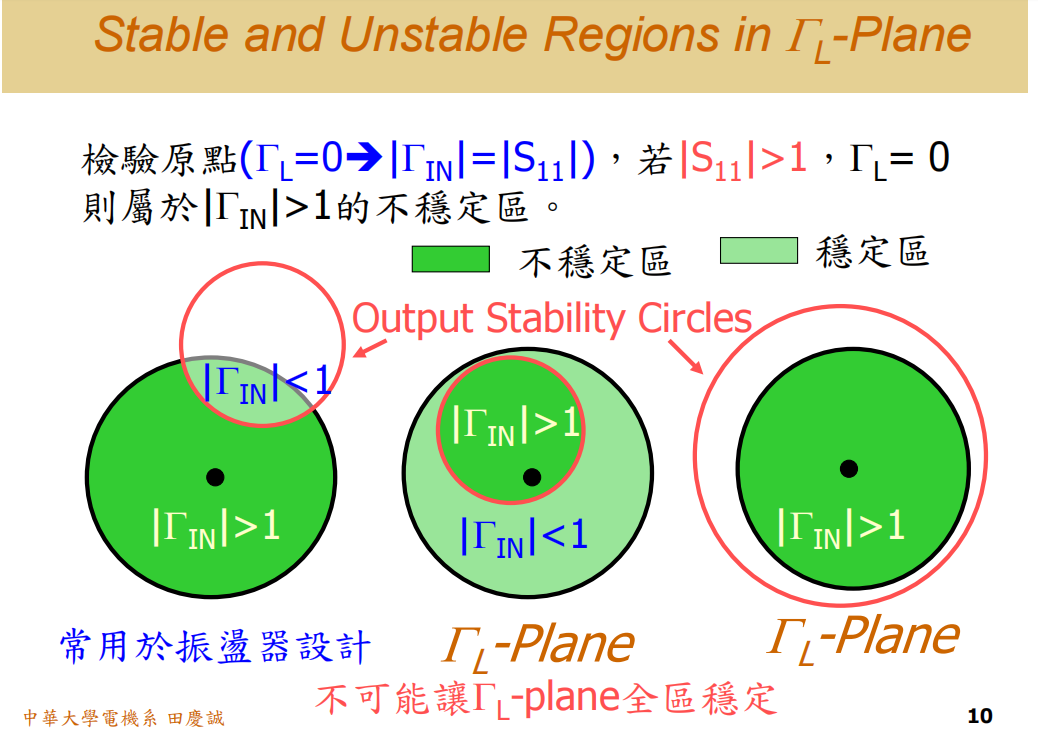
在 ΓLΓ_LΓL = 0 这一点，ΓINΓ_{IN}ΓIN = S11S₁₁S11，而 S11S₁₁S11 > 1，

那就意味着ΓINΓ_{IN}ΓIN > 1

而我们之前学过，这个圈圈的边界对应 ΓINΓ_{IN}ΓIN = 1。(输出稳定圆就是根据 ΓINΓ_{IN}ΓIN = 1所画出来)

既然原点的 ΓINΓ_{IN}ΓIN > 1，那就说明原点所在区域是不稳定的 。

所以，其实整个平面就被圆圈边界分成了两个区域，包含原点的区域就是不稳定区，剩下部分才是稳定区 。我们只需要看原点那一点就好了。

那么，有没有可能实现无条件稳定呢？有没有可能整个区域都稳定？

如果晶体管的 S11S₁₁S11 大于 1，我们说那就不可能实现无条件稳定。

这时候该怎么办呢？

我们可以通过添加电阻来吸收多余的能量 ，把 S11S₁₁S11 降下来，让它小于 1，这样才有可能实现稳定。其实就是把多余的能量吸收掉，让反射系数降下来。

这种 S11S₁₁S11 > 1 的情况常用于振荡器设计。在这种情况下，无论你怎么选择 ΓLΓ_LΓL，几乎整个区域都不稳定。这种特性反而使得设计振荡器的成功率更高。
所以，不稳定区域越多，越适合设计振荡器 。

不过这种 S参数特性比较少见，更常见的还是我们之前讲的第二种情况，S11S₁₁S11 < 1 的情况更为常见。

一般用于放大器的晶体管，S11S₁₁S11 大多小于 1。

不过也有例外，比如某些功率放大器的 S11S₁₁S11 可能会大于 1，这也是功率放大器设计难度高的原因之一，当输出功率超过 1 瓦时，晶体管很容易产生振荡，设计不当就会振荡。

而一般小信号晶体管的 S11S₁₁S11 都小于 1，这点大家可以放心。

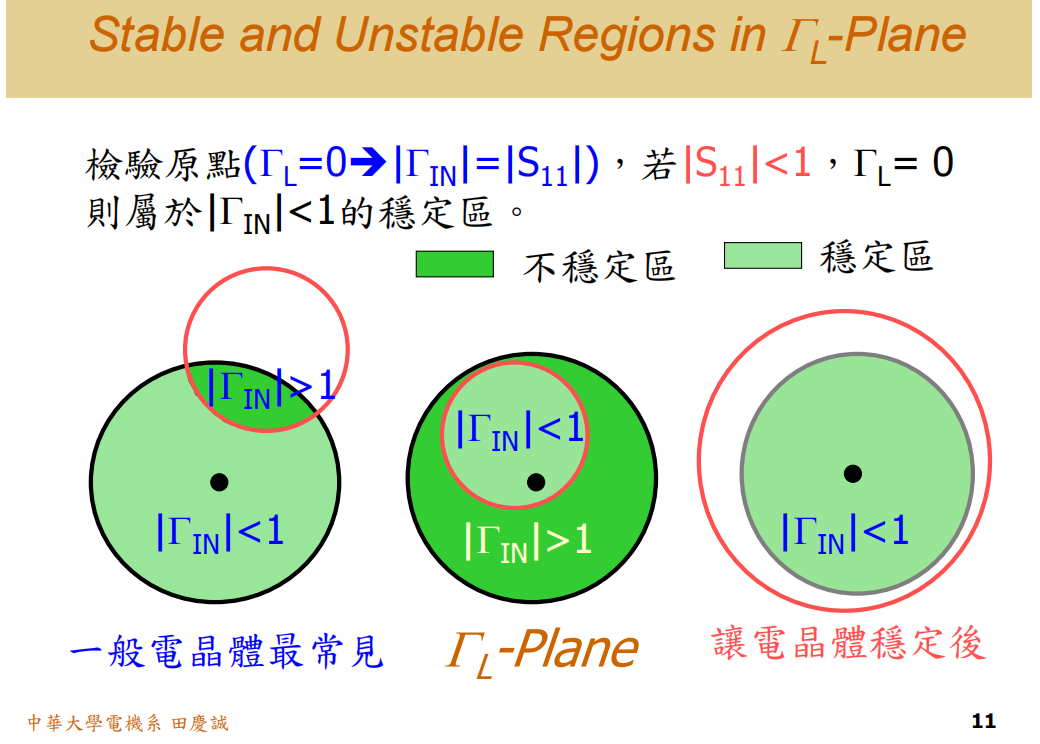
好，回到原点判断法。

当 ΓLΓ_LΓL = 0 时，如果 S11S₁₁S11 < 1，那么 ΓINΓ_{IN}ΓIN < 1，

所以原点处于稳定状态。

因此，包含原点的区域就是稳定区 ，也就是浅绿色部分。
如果我们能够将这个输出稳定圆推出去，使得整个ΓLΓ_LΓL史密斯圆图都处于稳定区，那就实现了无条件稳定。

那么 ΓSΓ_SΓS平面呢？原理是一样的。

在 ΓSΓ_SΓS 平面上，如果你随意选择 ΓSΓ_SΓS，可能会使得 ΓOUTΓ_{OUT}ΓOUT大于等于 1，导致输出不稳定，触发振荡条件。

在ΓSΓ_SΓS 平面上，我们对应的是 Input Stability Circle（输入稳定圆）。

如果 S22S₂₂S22 > 1，那么原点（ΓSΓ_SΓS = 0）就不稳定，对应的深橘色区域都是不稳定的。

而如果 S22S₂₂S22 < 1（这种情况更常见），那么当ΓSΓ_SΓS = 0 时，ΓOUTΓ_{OUT}ΓOUT = S22S₂₂S22 < 1，所以原点是稳定的，进一步说，包含原点的浅橘色区域都是稳定区。

此时我们的目标就是将这个输入稳定圆推出去，使得整个ΓSΓ_SΓS平面都稳定。这样，无论怎么设计输入匹配网络，都不会引发振荡。

接下来，我想向大家证明一个重要的概念。

曾经有同学问："老师，有没有可能前级不稳定，但后级稳定？或者反过来，后级不稳定，但前级稳定？有没有一种振荡器是前级振荡，后级不振荡的？"

实际上，振荡是不分前后级的。你从电路的任何一个地方接出来，它都会振荡。因为整个电路一旦满足振荡条件，任何一个截面都会振荡。

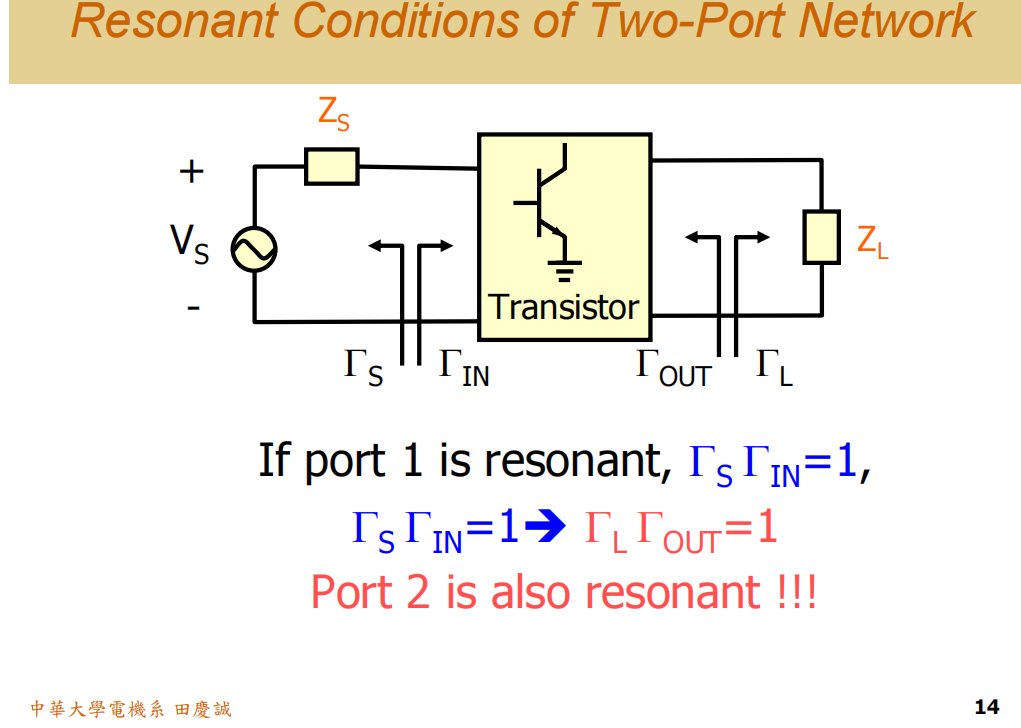
我来证明给大家看：

已知当 ΓINΓ_{IN}ΓIN ∙ ΓSΓ_SΓS = 1 时，满足振荡条件。

我们可以推导出，在另一个截面，ΓOUTΓLΓ_{OUT} Γ_LΓOUTΓL 也等于1。

这意味着，如果前级振荡，后级也绝对无法幸免，整个电路都会振荡 无论你在哪个位置截取，都会满足振荡条件。这就是振荡条件的传递性。

根据这个原理，我们在设计电路时，ΓLΓ_LΓL 和 ΓSΓ_SΓS 都是我们自己选择的。那么，我们是否需要分别在 ΓSΓ_SΓS 平面和 ΓLΓ_LΓL 平面上都进行稳定圆推出去的操作呢？是否需要做两次？

其实，只需要做一次就够了。

本质原因就在于:输入和输出的稳定性是相互关联、成对出现的

左边这是 ΓSΓ_SΓS 平面上的 Input Stability Circle，右边是ΓLΓ_LΓL平面上的 Output Stability Circle。

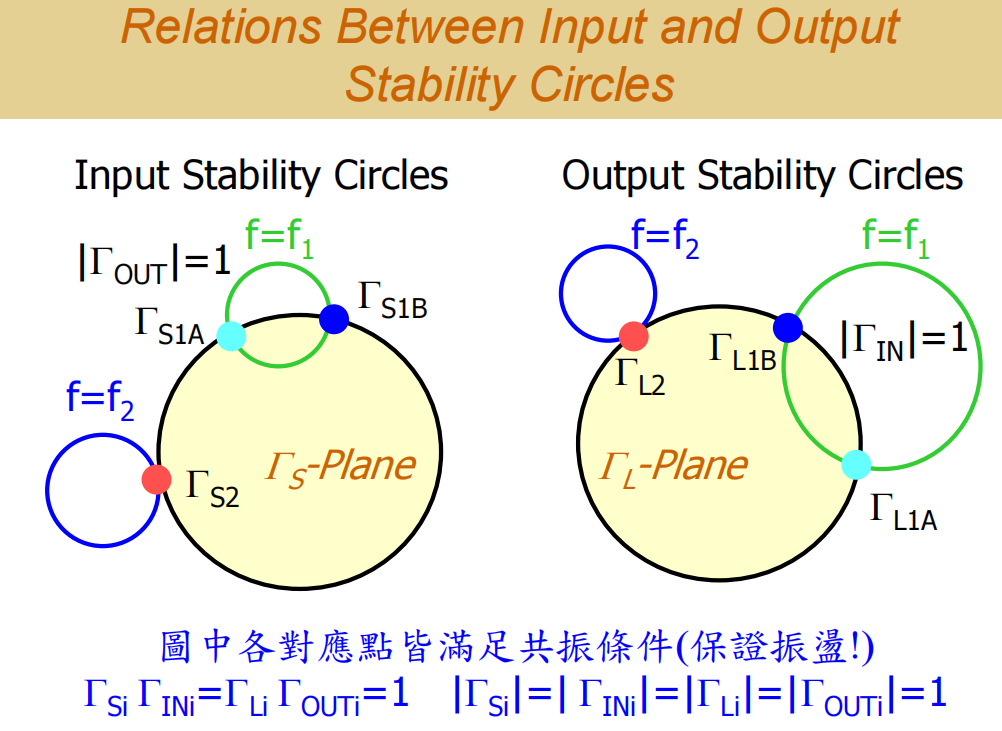
假设我们在 ΓSΓ_SΓS平面上选择了一个"危险点"（这个点会导致输出端 ΓOUTΓ_{OUT}ΓOUT > 1，不稳定）。那么，在 ΓLΓ_LΓL平面上，必然存在一个对应的"危险点"（这个点会导致输入端 ΓINΓ_{IN}ΓIN > 1，不稳定）。

如果我们同时选择了这一对"危险点"，那么电路就完全满足了振荡条件，必然会产生振荡。

同理，如果在稳定区内选择对应的点，也是一样的道理，稳定点也是成对出现的。

由于这种危险的成对性，两个稳定圆的"行为"是同步的：

当电路处于潜在不稳定状态时，两个稳定圆都有一部分在史密斯圆图单位圆之内。(存在相同的危险区域)

当我们通过设计（比如添加稳定电阻或调整匹配电路）将其中一个稳定圆完全推出史密斯圆图时，电路就达到了"无条件稳定"状态。

此时，另一个稳定圆也会自动地、同步地被完全推出史密斯圆图 .(保证没有危险点对应)

所以，我们只需要在一个平面上进行操作就可以了。比如，只需要在输入匹配设计时确保稳定，输出匹配就不需要再做了。

1.6 实际例子说明

来，我们看一个具体范例。建议大家回去用 ADS 软件来做，我这里是用 Microwave Office 演示的。

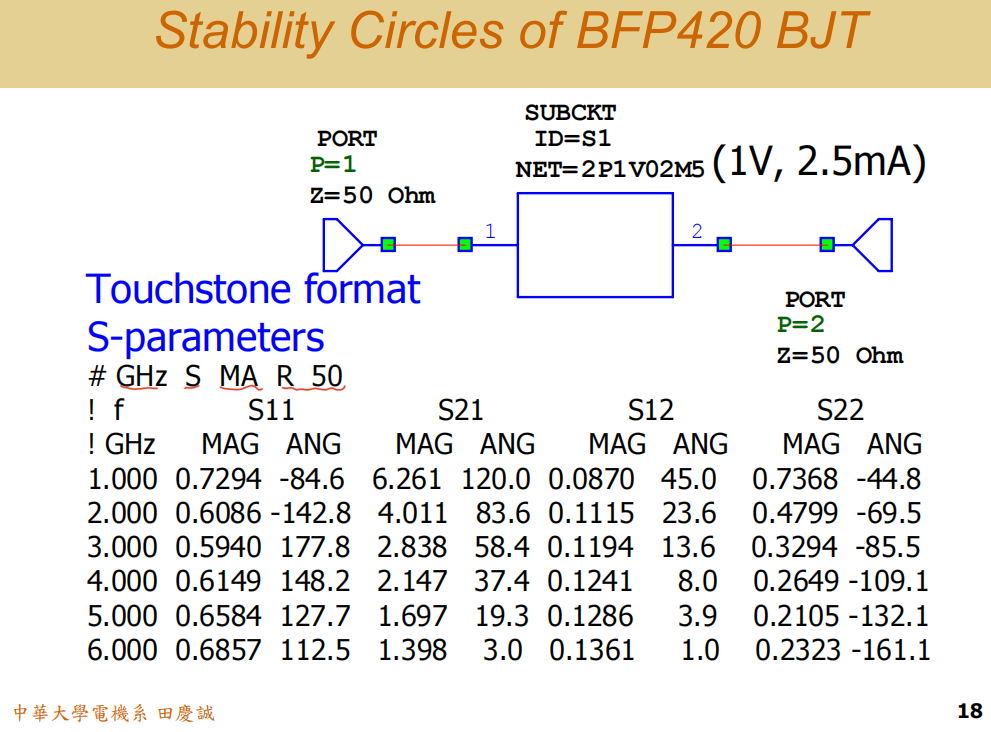
首先，我们调用一个晶体管的 S 参数模型。这里的关键是正确编写 S 参数文件：

第一行以 # 开头，接着指定频率单位，比如 GHz, Hz, kHz 等。
然后声明参数类型，是 S、Y 还是 Z 参数？我们这里当然是 S 参数。
接下来定义 S 参数的格式，常见的有：
- MA：幅度和相位
- RI：实部和虚部
- DB：幅度为 dB 值，后面跟相位
  我们这里简写为 DB 即可。
最后，指定参考阻抗，通常是 50 欧姆。这表示 S 参数是在 50 欧姆系统下测量的。

这个范例中，晶体管的 S 参数频率范围是从 1 GHz 到 6 GHz。我们使用的晶体管是 BFP420，一种硅基晶体管，偏置点在 2.5 mA。

疑问:晶体管S参数只涵盖了1-6GHz的范围，但低频稳定性恰恰是关键。没有低频S参数，我们该如何评估？

如果仅使用1-6GHz的S参数，软件在模拟低频时会通过多项式拟合外推数据。这种基于3GHz、2GHz、1GHz等高频率点去拟合低频特性的方法，其结果基本不准确，没有参考价值。因此，S参数在1-6GHZ区间内的拟合是有效的，但向更低或更高频率外推得到的S参数则不可靠。

最有效的方法是找到并使用该器件的奈奎斯特模型。奈奎斯特模型在低频段的精度通常足够高，可以接受。通过这种方式，我们就能获得可信的低频参数，进而检查低频段的稳定性。

请注意： 当你查找一个晶体管的 S 参数时，会发现它往往提供十几组不同的数据。这是因为 S 参数会随偏置点变化而变化。所以，同一个晶体管在不同偏置下会有不同的 S 参数。

准备好 S 参数文件后，我们在软件中将其前面连接一个 port 1，后面连接一个 port 2。这样，软件就可以开始进行计算了。

接下来，我们让软件画出 Output Stability Circle（输出稳定圆）。结果如下：

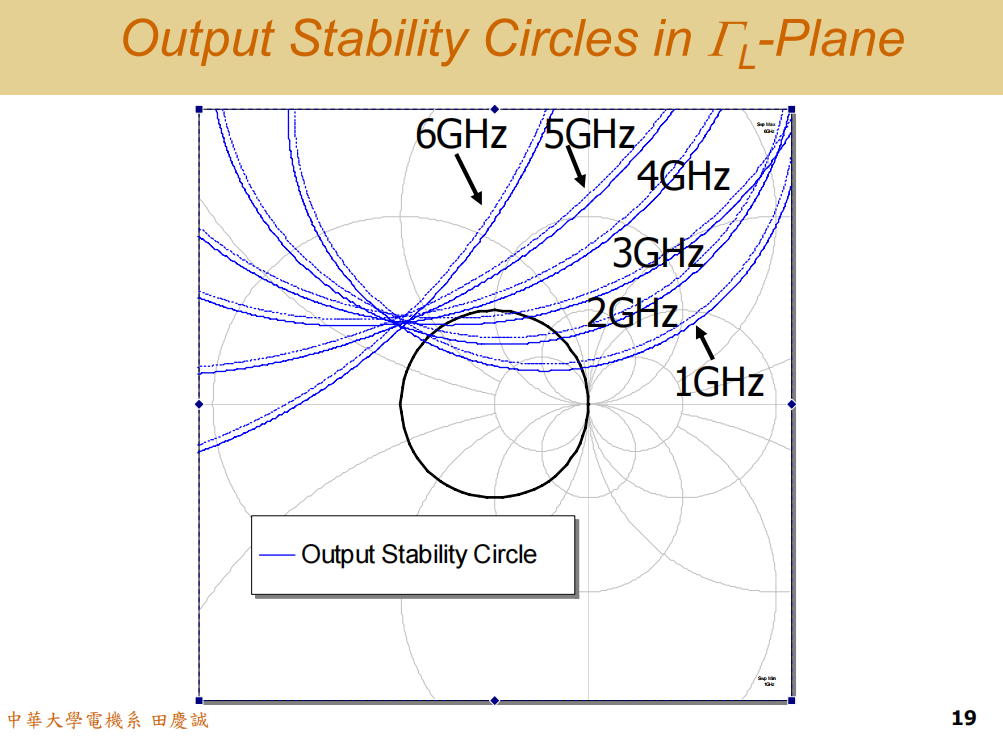
图中这个黑色的、半径为 1 的圆，就是我们的 ΓLΓ_LΓL平面（史密斯圆图）。

在 1 GHz 时，稳定圆出现在这个位置。
这时，我们需要判断哪一区是稳定区？是上面还是下面？

根据我们前面所说，在 ΓLΓ_LΓL 平面上，这个稳定圆的边界对应的是 ΓINΓ_{IN}ΓIN = 1。要判断稳定区，我们需要看 S11S₁₁S11。

在 1 GHz 时，S11S₁₁S11 大约是 0.7，小于 1。S22S₂₂S22 也同样小于 1。
频率越低，反射系数通常越大，电路越趋向于不稳定。
因为 S11S₁₁S11 < 1，所以包含原点的区域是稳定区 。软件会用虚线标示 出不稳定区。

一个重要的规律：频率越高，晶体管越趋向于无条件稳定。

到 2 GHz 时，稳定圆开始向外移动。
3 GHz 时，它快要移出单位圆了。
4 GHz 时，它已经完全移到单位圆外面了。这时电路就达到了无条件稳定。

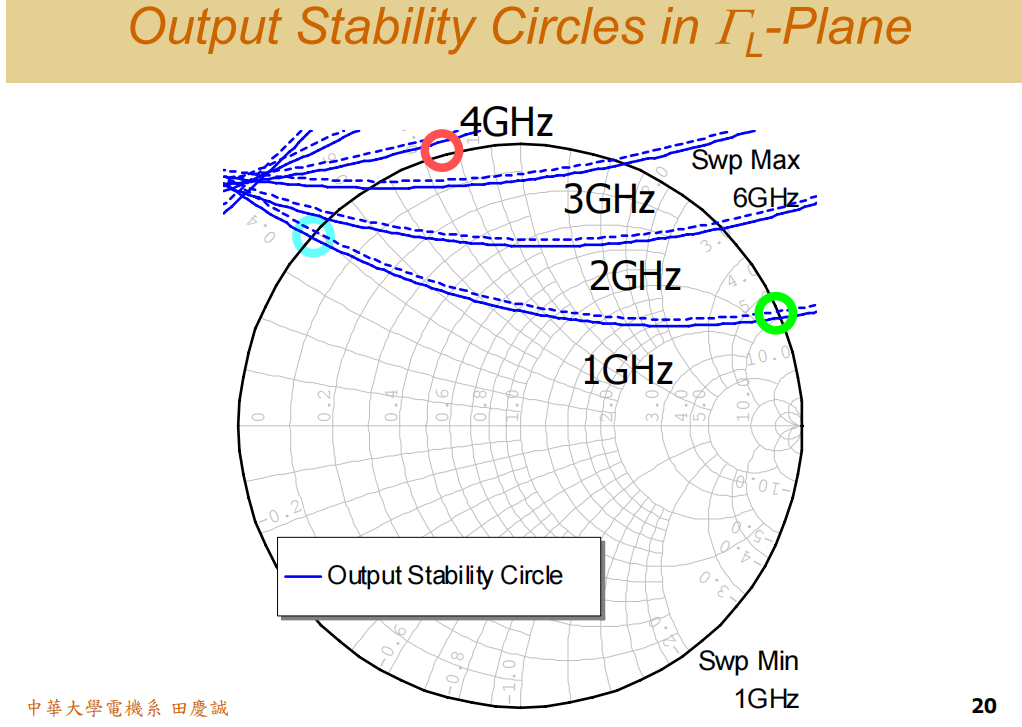
请大家自己调整频率，找到在 3.8 GHz 左右，稳定圆刚好与单位圆相切的那个点。

接下来，我们画出 Input Stability Circle（输入稳定圆）。

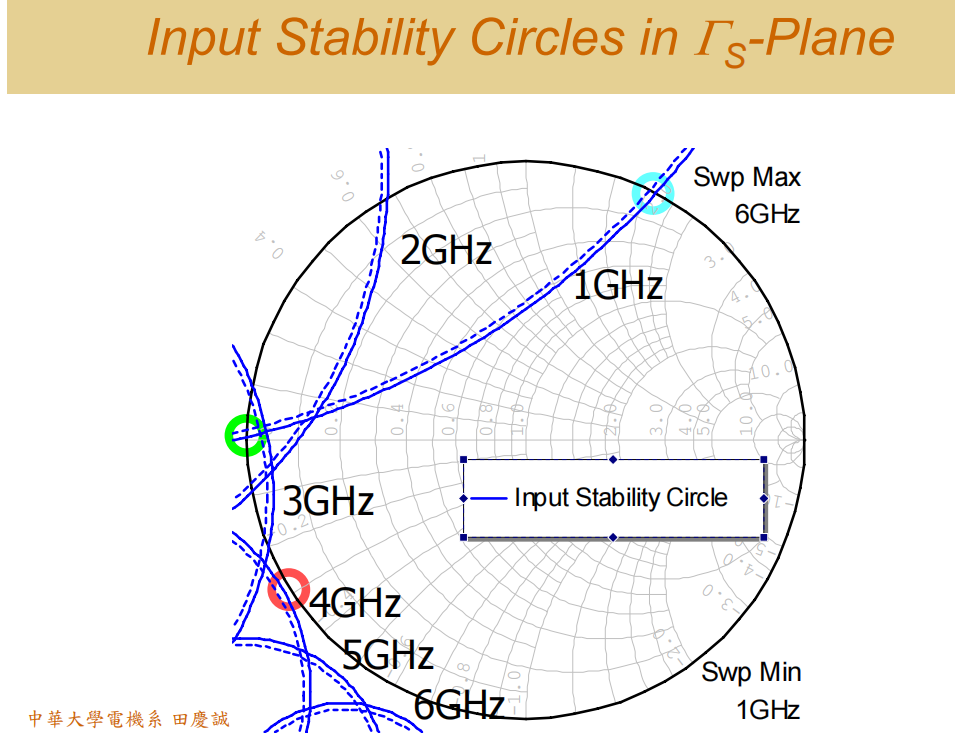
在 1 GHz 时，输入稳定圆上的点会与输出稳定圆上的点一一对应。
请大家将这些对应点的反射系数（ΓIN,ΓOUT,ΓS,ΓLΓ_{IN}, Γ_{OUT}, Γ_S, Γ_LΓIN,ΓOUT,ΓS,ΓL）都计算出来，并验证它们是否满足振荡条件。

这个范例也清晰地展示了：当输入稳定圆（红色）被推出单位圆时，输出稳定圆（蓝色）也同步被推出。请大家务必用软件验证这一点。

1.7 数学判据：K-Δ 与 μ 因子

以上是图解法，接下来我们学习更常用的数学判断法 ------直接用稳定性因子来判断，这在实际工程中更为高效。

首先，我们学习无条件稳定的充要条件 。这意味着条件和结论是双向的：如果电路无条件稳定，则下列条件成立；反之，如果下列条件成立，则电路无条件稳定。

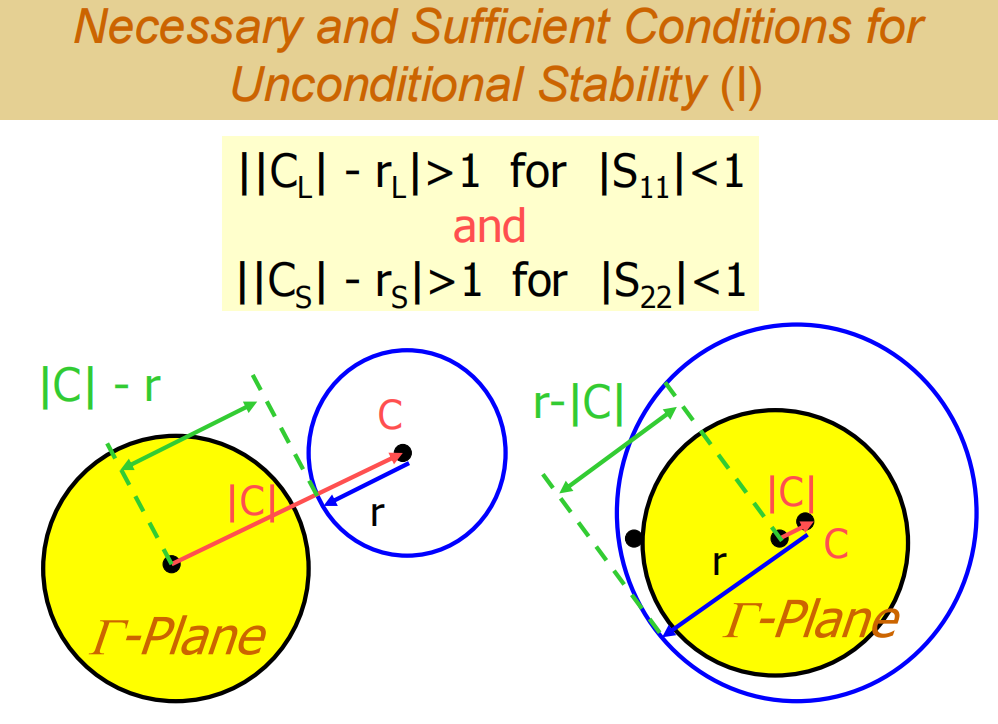
总共有四个条件需要同时满足：

|S11S₁₁S11| < 1
|S22S₂₂S22| < 1
|CL∣−∣RLC_L| - |R_LCL∣−∣RL| > 1 (对于 ΓLΓ_LΓL 平面)
|CS∣−∣RSC_S| - |R_SCS∣−∣RS| > 1 (对于 ΓSΓ_SΓS 平面)

解释一下：

如果 |S11S₁₁S11| 或 |S22S₂₂S22| 大于 1，电路绝不可能无条件稳定。必须先通过加电阻等方法将它们降到 1 以下。
|CLC_LCL| 是ΓLΓ_LΓL平面上稳定圆的圆心到原点的距离，|RLR_LRL| 是稳定圆的半径。|CLC_LCL| - |RLR_LRL| > 1 意味着稳定圆被完全推出了单位圆。

由于输入和输出稳定性是同步的，一个稳定圆被推出，另一个必然也被推出。因此，我们只需要验证其中一组条件即可(如1,3或者2,4) ，无需四个全部检查。

为此，我们引入一个参数 μ。

μ1 是针对输出稳定圆的，它确保 ΓINΓ_{IN}ΓIN = 1 的圆被推出。
μ2 是针对输入稳定圆的，它确保 ΓOUTΓ_{OUT}ΓOUT = 1 的圆被推出。
关键结论： 只要 μ1 > 1 ，就必然有 μ2 > 1 。反之亦然。所以实践中，我们只需计算 μ1 或 μ2 中的一个即可。

因此，简化的数学判断法只需要三个条件：

|S₁₁| < 1
|S₂₂| < 1
μ1 > 1 (或 μ2 > 1)

第二种，也是最常用的方法 是使用 稳定性因子 K。

前提同样是 |S₁₁| < 1 和 |S₂₂| < 1。

然后计算 K 因子，要求 K > 1 。

同时，还需要一个辅助条件，通常要求 |Δ| < 1 （其中 Δ=S11S22−S12S21Δ = S₁₁S₂₂ - S₁₂S₂₁Δ=S11S22−S12S21）。
请注意： 很多教材会忽略 |Δ| < 1 这个条件，但严谨的设计必须两者同时检查。仅满足 K > 1 是不够的。

除了 |Δ| < 1外，我们还可以验证另外一个参数B1，同样在 |S11S₁₁S11| < 1 的前提下，要求 B1 > 0。这个因子在处理共轭匹配时非常有用。

练习:

请大家根据我的方法，绘制出 μ1, μ2, K 和 B1 随频率变化的曲线。

在低频（如 1 GHz），你会发现 μ < 1，K < 1，这表示不稳定。
随着频率升高，在 ~4 GHz 附近，μ 和 K 会同时等于 1。这一点正好对应输出稳定圆与单位圆相切。
频率再升高 ，μ > 1，K > 1，B1 > 0，电路进入无条件稳定区。

这个练习能让你直观地理解稳定性如何随频率变化。我强烈建议大家把所有这些图表都亲手做一遍，印象会更加深刻。除了图形化方法，我们还可以用数学公式来精确判断。

1.8 实际例子说明

当我们拿到一个晶体管，第一步要测量和分析什么？就是下面这张图，大家必须先把这张图搞懂。

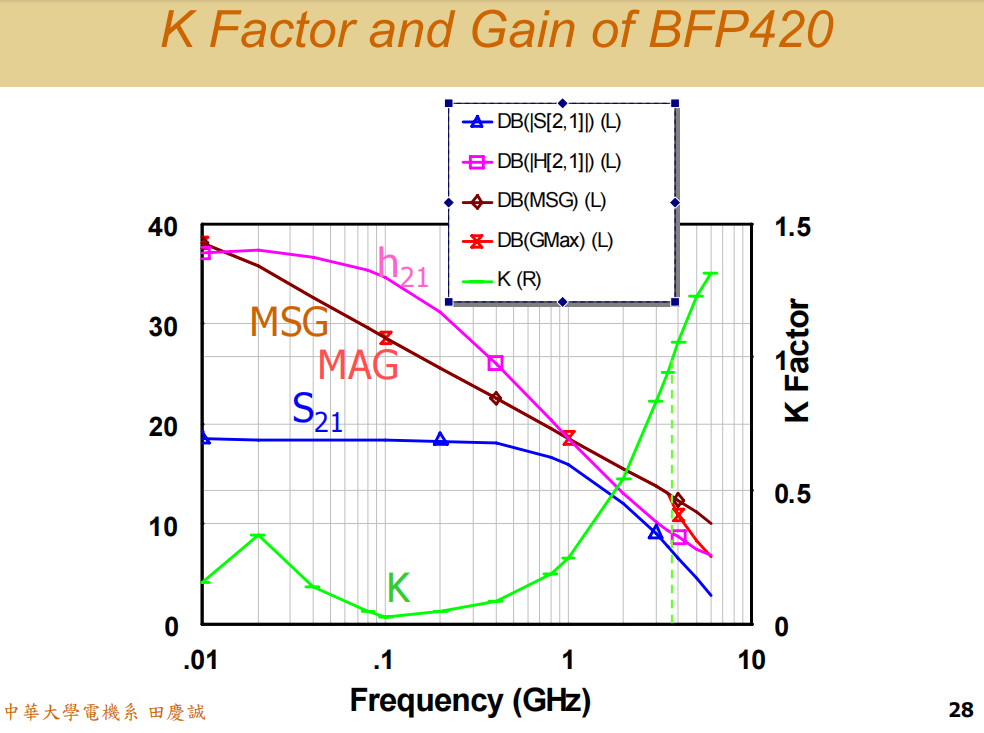
之前我们已经教过 MSG(最大稳定增益) 的计算方法：MSG=∣S21∣∣S12∣MSG = \frac{|S₂₁|}{|S₁₂|}MSG=∣S12∣∣S21∣,然后dB值取10∗log10(mag)10*log10(mag)10∗log10(mag)。

还有 MAG（最大可用增益） ，它的公式是 MAG=∣S21∣∣S12∣∗(K−K2−1)MAG = \frac{|S₂₁|}{|S₁₂|} * (K - \sqrt{K² - 1})MAG=∣S12∣∣S21∣∗(K−K2−1 )。

S参数可以转换成其他参数，比如 H参数 。h21h₂₁h21其实就是S21S₂₁S21。当频率降低时，h21h₂₁h21会掉到 0 dB（也就是增益为 1）的频率点，这个频率被称为 ftfₜft(截止频率) 。

那么，S21S₂₁S21掉到 0 dB 的频率叫什么？叫 fsfₛfs ，但这个不常用，更常用的是 fmaxfₘₐₓfmax（最大振荡频率） 。
问题来了：这颗晶体管的 fmaxfₘₐₓfmax 是多少？

我们现在只有到 6 GHz 的 S 参数，后面的数据无法计算，算出来也不准。那我们怎么把这条曲线延伸下去呢？

我们来看这张图。红色的曲线代表 MAG 。大家有没有发现一个奇怪的现象：红色曲线只在某一段频率之后才出现？而且，它恰好是从 K > 1 的那个点开始出现的。

为什么会分开？

根据 MAG 的公式，当 K < 1 时，公式里的 K2−1\sqrt{K² - 1}K2−1 会变成对负数开根号，结果是个虚数！增益怎么可能有虚数呢？所以，当 K < 1 时，MAG 实际上不存在 。

那么软件画的是什么呢？在 K < 1 的区域，软件通常画的是 MSG 。所以在那段频率里，红色和咖啡色的曲线其实是重合的。只有当 K > 1 之后，它们才分开，这时 MAG 才真正存在。
另一个问题：为什么 MAG 会比 MSG 低？

看公式，当 K > 1 时，(K−K2−1)(K - \sqrt{K² - 1})(K−K2−1 ) 这项必然小于 1。所以，稳定之后你能实际获得的最大可用增益，会比最大稳定增益要低。晶体管真正的增益能力就是这条红色曲线。

这条红色曲线的下降斜率是多少？大约每倍频程下降 6 dB。根据这个斜率，我们可以反推估算出，这颗 BJT 的 fmaxfₘₐₓfmax 大约在 10 GHz 左右。

这张图告诉我们什么？

很多人看图没感觉，我来总结几个关键结论：

低频高增益与稳定性矛盾 ：在低频时，晶体管的增益很高，但 K 因子很小，这意味着它处于潜在不稳定状态 。增益高不一定是好事，它很容易让放大器变成振荡器。所以，一般单级放大器的增益最好不要超过 15 dB，否则稳定性会非常差。
如何选择晶体管？
- 你的放大器的 fmaxfₘₐₓfmax 不是越高越好。比如，你要做一个 2.4 GHz、增益 10 dB 的放大器。根据固定的下降斜率，你选择的晶体管 fₘₐₓ 在 10 GHz 左右是比较合适的。
- 如果你选了一个 fmaxfₘₐₓfmax 高达 40 GHz 的"极品"晶体管，那么它在 2.4 GHz 的增益会非常高（可能超过 20 dB）。这会导致电路极其不稳定 ，很容易在低频和高频都产生振荡，而且想让电路稳定下来会非常困难。同时，这也是浪费成本。

最终设计验收标准

当完成整个放大器的设计（包括前后级匹配）后，我必须要求你们提供一张图：整个放大器级的 K 因子和增益随频率变化的曲线。（注意，这不是单个晶体管的，而是整个放大器的）

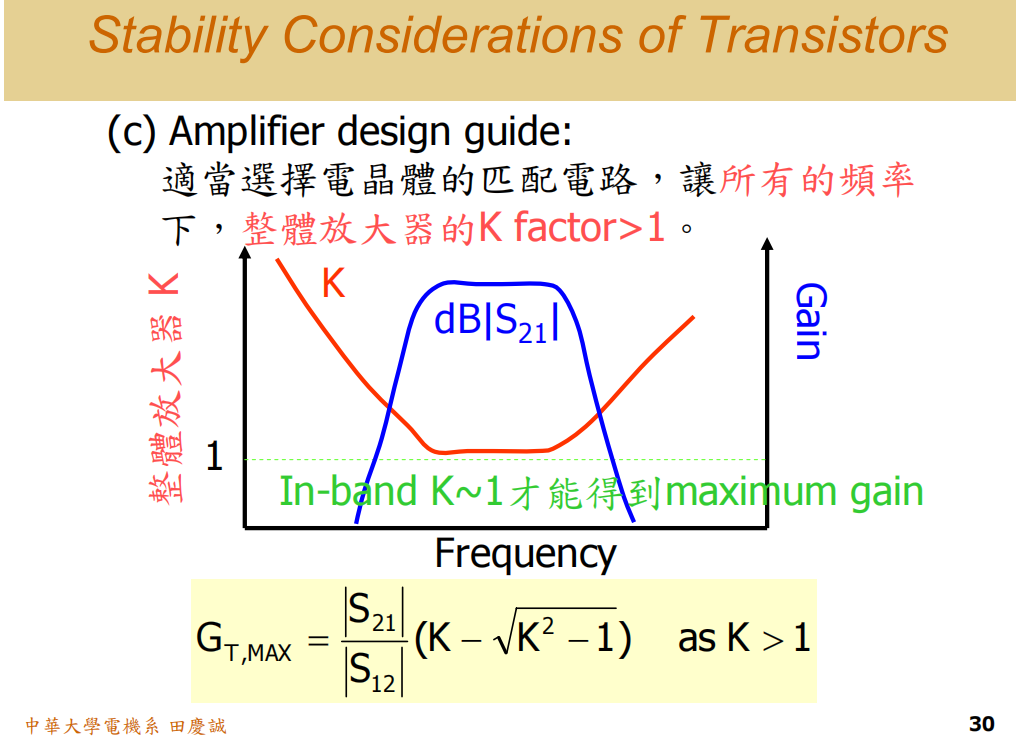
我对这张图的要求是：

K 因子：
- 在整个频带内，K 值要略大于 1（通常会将K值设计在1.05至1.1之间,例如 1.1） 。为什么？
  - 从 MAG 公式可知，当 K=1 时，增益最大（MAG=MSG），但处于临界稳定，很危险。
  - K 值太大（比如做到 2），说明你用了太多电阻去稳定，增益损失会非常严重。
  - 经计算，K=1.05时，最大可用增益比MSG低约1.37dB。
    K=1.1时，约低1.97dB（近似2dB）。因此，业界规定来说"MSG - 2dB "并保证K>1是一个常见且稳健的设计目标。这确保了电路有足够的稳定裕量来应对元件偏差和环境变化，是实现可量产、高可靠性设计的关键。
- K 值曲线必须是 "一去不回头" 地保持在 >1 的水平。如果曲线在某个低频点变得平坦甚至下降，就意味着存在低频不稳定的风险，这是我们必须避免的。
- 物理原因：在极低频段（例如接近1MHz），寄生效应基本消失，S21S_{21}S21很高而S12S_{12}S12极低，器件接近理想的单向性元件，因此通常是绝对稳定的。
增益曲线：
- 在你需要的通带内，增益要尽量平坦。
- 在通带外，增益必须被坚决地压制下去 。这样做有两个好处：
  - 提高稳定性：消除带外振荡的可能。
  - 降低噪声：防止带外的噪声和干扰信号被放大，从而影响整体性能。

一个合格的最终设计，其增益和 K 因子曲线应该符合上述形态。

1.9 工程实践

【实践警告】：1.测量仪器的正确使用

很多同学在做高功率放大器测量时，一上来就把电路接上网络分析仪，这是非常危险的！

之前我们用的一个放大器模块，一接上网络分析仪，屏幕上的曲线就变得"毛毛躁躁"。这其实是放大器已经自激振荡 了，振荡信号串进了分析仪。再这样下去，很可能烧毁价值不菲的网络分析仪！
正确步骤 ：

不要先接网络分析仪！ 先接上频谱分析仪。
将放大器的输入端接 50 欧姆负载，输出端接频谱分析仪（其输入阻抗也是 50 欧姆）。
上电后，用频谱仪从低频到高频仔细扫描，检查有没有异常的尖峰（振荡信号） 。
用手轻触电路，如果尖峰的频率随之变化，那基本可以确定是电路自激。
必须先解决振荡问题，才能连接网络分析仪进行测量！

【实践警告】：2.关于并联晶体管以增加功率

有人问：把两个晶体管并联，输出功率能增加一倍吗？

功率：是的，理论上输出功率可以翻倍。
增益：那增益也会翻倍吗？不会。增益是输出/输入的比值，并联并不会改变这个比值。实际上，增益反而会下降。

为什么？

阻抗变化 ：晶体管并联后，输入和输出阻抗会急剧下降（根据并联公式），可能变得非常低。这导致匹配变得极其困难，且稳定性（K因子）会变得非常差，S11S₁₁S11 和 S22S₂₂S22 甚至可能大于1。
稳定代价 ：为了让这样一个不稳定的系统稳定工作，你必须加入电阻来消耗掉多余的能量。这个过程会吃掉很多增益。所以，最终你实际得到的增益，可能比只用单个晶体管时还要低。

因此，并联晶体管以获取高功率是需要付出代价的，并不是并得越多越好。

第二部分：系统性的稳定技术

一些教材会介绍一种方法：在目标频率（如2.4GHz）的史密斯圆图上，分别画出源和负载端的稳定圆，然后选择落在稳定区域内的ΓSΓ_SΓS和ΓLΓ_LΓL值。

原则：选择的工作点应远离稳定圆的边界，以防因元件公差、PCB工艺偏差或外部接口阻抗变化（实际电路前后级很少是完美的50欧姆）导致工作点漂移到不稳定区，引发振荡。

但这种方法在业界通常不被接受，它存在重大风险，只要不稳定区在圆图上存在，就始终存在因不可控因素落入其中的风险 。产品量产后的批量退货风险是企业无法承担的。

并且该方法只保证了单一设计频率的稳定性。但在其他频点（尤其是低频），电路可能完全处于不稳定区，而我们必须确保晶体管在所有频点的K因子都大于1。

因此，业界的标准做法是：必须保证晶体管在所有频率下都是无条件稳定的(K > 1) 。一个良好的稳定性设计，其稳定圆应呈现如下趋势：在目标频段（如2.4GHz），稳定圆紧挨着史密斯圆图的边界（此时K≈1，增益最大）。随着频率降低，稳定圆应迅速向外移动，远离史密斯圆图 。这意味着在低频段，稳定区域非常大，电路非常稳固。

我们的设计目标就是通过稳定性网络，将这些在低频段"侵入"史密斯圆图的不稳定区全部"踢出去"。

2.1 串联电阻

我们可以在晶体管的输入端 或输出端串联一个电阻来实现稳定。

关键原则 ：只选择一端（输入或输出）串联，切勿两端都加。
原因:当你在输入端串联电阻并将输入稳定圆 "推" 出史密斯圆图外时，输出稳定圆也会自动被推出去。反之亦然。因此，只需处理一端即可。

如何选择串联位置？这是一个重要的设计权衡：

对低噪声放大器的建议 ：电阻应加在输出端。因为在输入端串联电阻会直接恶化整个系统的噪声系数，这对于追求低噪声的设计是不可接受的。
对功率放大器的建议 ：电阻应加在输入端。因为在输出端串联电阻会消耗宝贵的输出功率，导致效率降低。为了稳定而牺牲一点增益是可以接受的，但绝不能牺牲输出功率。

串联电阻的实现原理（以输入端为例）：

目标：将输入稳定圆推出史密斯圆图。
操作：我们将"晶体管"视为"晶体管+串联电阻"这个新组合。这个新组合的输入反射系数（ΓS′Γ_S'ΓS′）与原始晶体管的输入反射系数（ΓSΓ_SΓS）之间存在一个明确的转换关系。
核心转换 ：从ΓSΓ_SΓS到 ΓS′Γ_S'ΓS′ 的变换，在阻抗图上相当于减去一个电阻值 。这个变换沿着等电抗圆向史密斯圆图的左边缘（电阻为零处）移动。
计算电阻值 ：
- 在史密斯圆图上，找到一个与原始输入稳定圆相切的等电阻圆。
- 读出该等电阻圆的归一化电阻值（例如 0.19）。
- 计算实际电阻值(假设特征阻抗为50Ω)：R = 0.19 × 50Ω = 9.5Ω。
- 这个 9.5Ω 就是从 Γ_S 点变换到史密斯圆图边缘（零电阻点）所需减去的电阻值。因此，需要串联的稳定电阻就是 9.5Ω 。

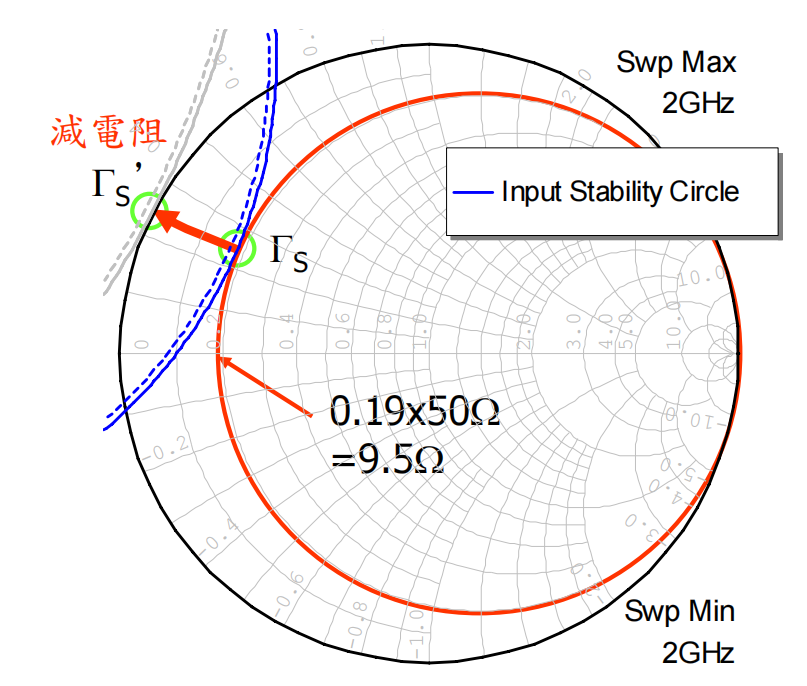
注意事项：

这种方法并非万能。在某些情况下，稳定圆可能包围了整个史密斯圆图中心。此时，通过串联电阻"减阻"的路径可能无法有效将整个不稳定区推出，这种方法就会失效。设计师需要根据稳定圆的形状判断，如果串联无效，则需尝试其它方法。

我们同样可以在输出端串联电阻来实现稳定，其原理与输入端串联完全对称。

操作:在史密斯圆图上找到与输出稳定圆相切的等电阻圆。读出对应的归一化电阻值，例如，读出的归一化电阻值为 0.56，则所需串联的电阻为 R = 0.56 × 50Ω = 28Ω。

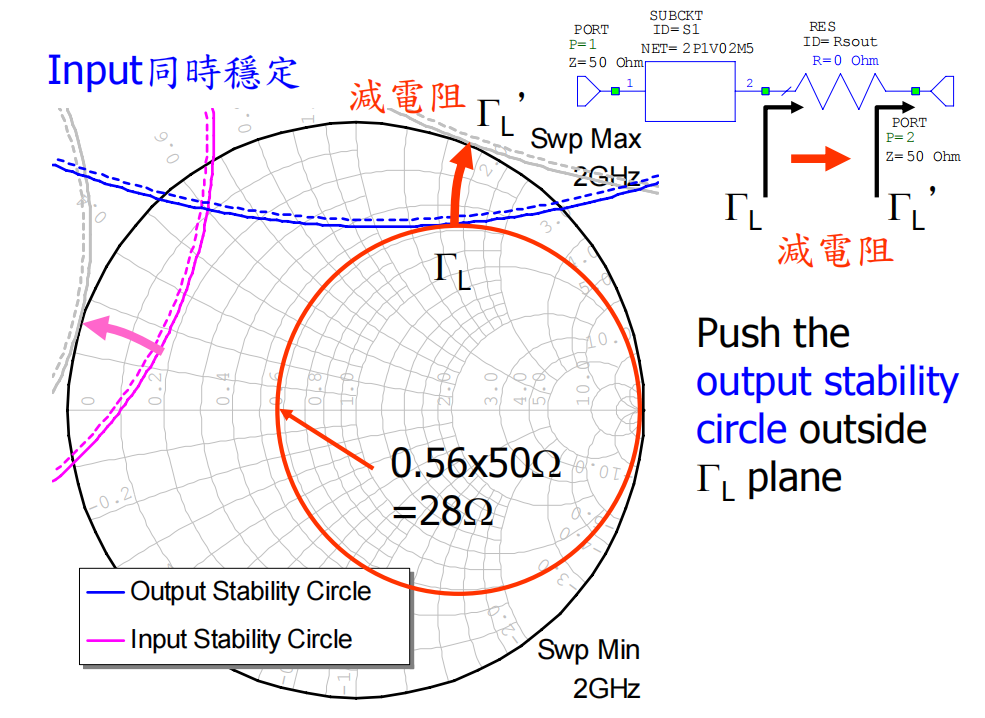
为何选择切点：

这个相切点代表了将整个不稳定区推出圆图所需的最大电阻值。只要这个点被推出，稳定圆上的其他所有点（所需电阻更小）都必然会被推到更外面的稳定区。通过软件仿真可以直观地验证这一点。

2.2 并联电阻

除了串联，也可以使用并联到地的电阻来实现稳定。同样，这个电阻可以加在输入端或输出端，只需选择一端即可。

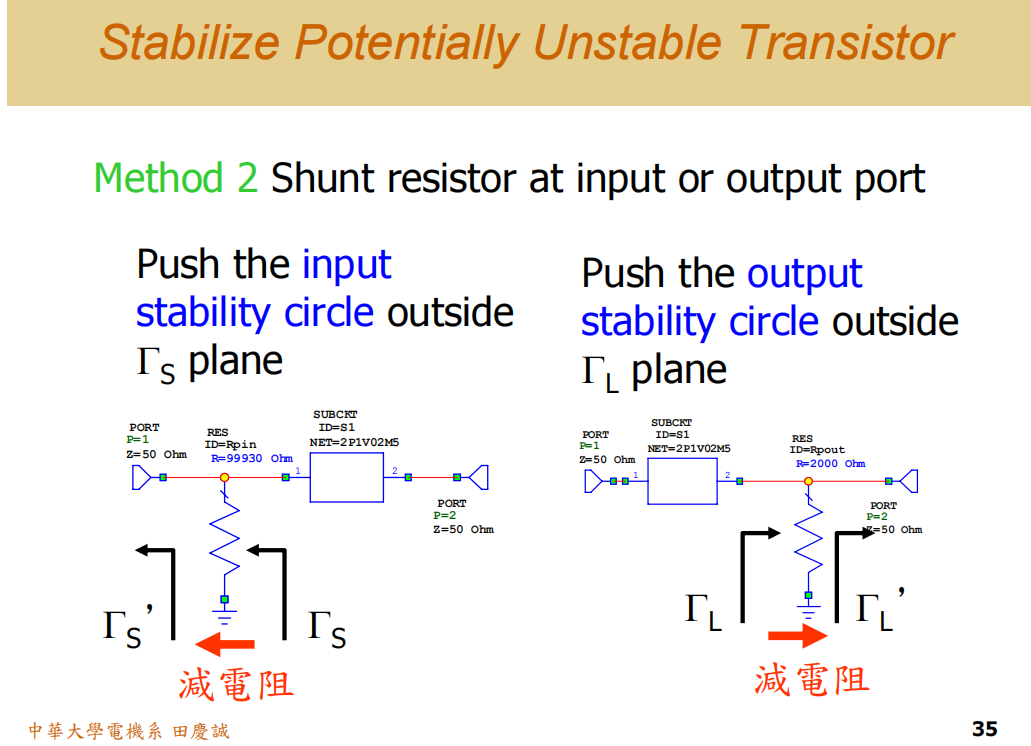
操作方法和串联电阻几乎完全一样，不过将寻找相切的归一化电阻圆，变为寻找归一化电导圆 。该等电导圆对应的归一化电导值,即为需要"减去"的电导。

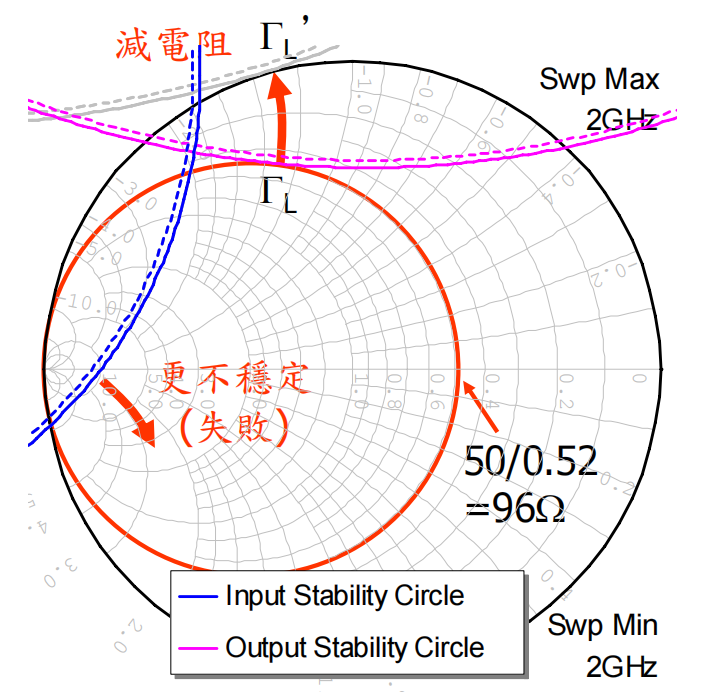
2.3 加入负反馈

这是另一种非常常见且有效的方法，主要包括两种类型：

串连反馈 ：如在源极（FET）或发射极（BJT）串联一个电阻或电感。这被称为源极/发射极退化反馈。
并联反馈：在晶体管的输出和输入之间并联一个电阻-电容网络。

负反馈不仅能提升稳定性，还能方便地控制增益，相关公式在教材中已有详细推导。与串联电阻不同，反馈电阻的取值通常需要通过仿真试错来确定，观察稳定圆的变化趋势。

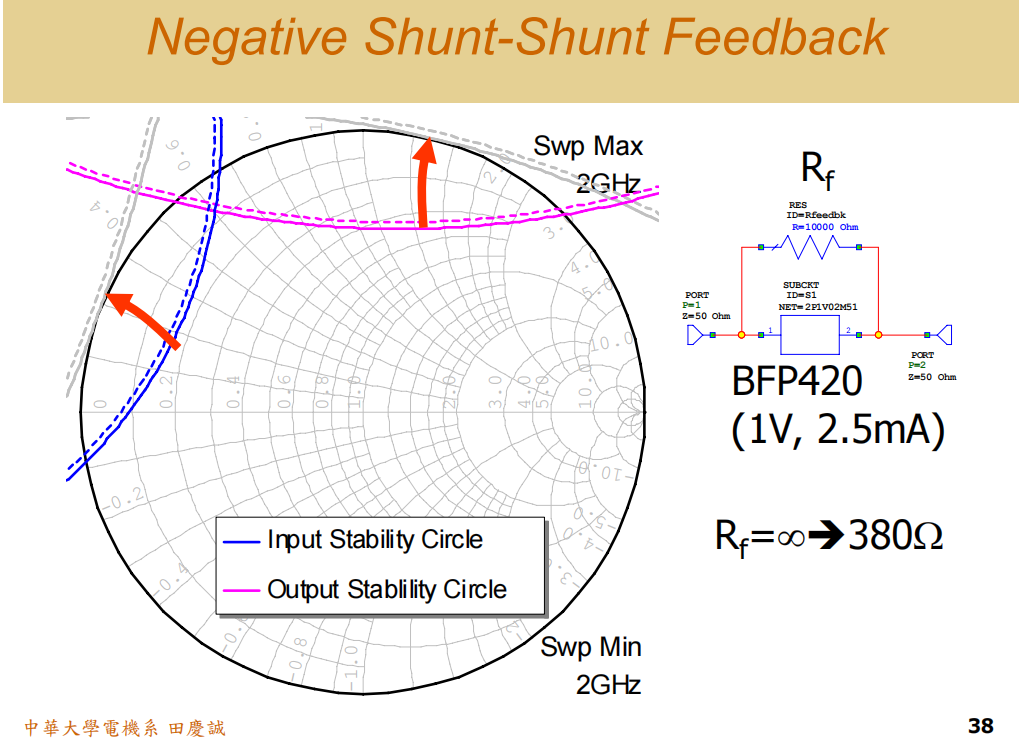
负反馈的优势：

卓越的宽带稳定性：负反馈能非常有效地抑制低频不稳定性，效果通常优于串联电阻。
简化阻抗匹配 ：引入负反馈会改变晶体管的输入输出阻抗。通过恰当选择反馈电阻，可以使其输入输出阻抗接近50欧姆，从而省去外部匹配电路，极大简化设计并节省芯片面积。市面上许多宽带放大器（如覆盖1-6GHz的产品）都采用此方法以实现小型化。

但凡事皆有代价，负反馈的主要缺点是：

增益下降：这是负反馈的基本特性。
噪声性能恶化：反馈电阻本身会引入额外噪声，并可能影响电路的噪声匹配。因此，追求超宽带性能往往意味着需要牺牲增益和噪声系数。

在实际仿真中，引入负反馈后，电路的增益曲线可能会在高频段出现异常凸起 。这通常是一个危险信号，表明在该频段反馈可能从负反馈转变为正反馈 ，从而引发电路振荡。

为什么会出现正反馈？在高频下，晶体管本身的相移会发生变化。当相移累积到一定程度时，反馈信号的相位可能从反相变为同相，负反馈就变成了正反馈。因此，设计时必须仔细检查全频段的稳定性，确保K因子在所有频率下都大于1。

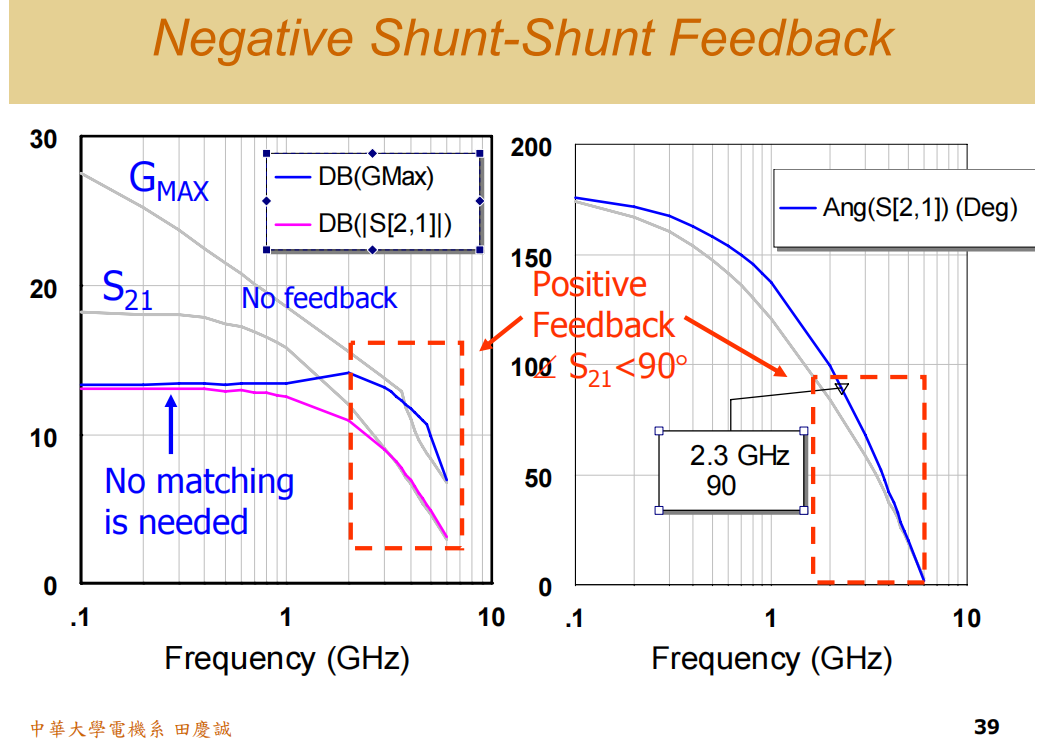
总而言之，负反馈是一种强大的工具，它能用简单的结构实现宽带稳定和简化的匹配。然而，设计师必须清醒地认识到其代价：增益的损失和噪声性能的下降。这种"增益换带宽"、"性能换通用性"的权衡，在追求超宽带性能时尤为明显。因此，负反馈非常适合用于对噪声要求不严、但需要覆盖多频段的多标准系统，而在追求极限噪声或增益性能的低噪声放大器、功率放大器中则需慎用。

2.4 频率选择性负载/反馈网络

我们之前介绍了三种基本的稳定方法：串联电阻、并联电阻和负反馈。它们都属于宽带稳定方法 ，即电阻在所有频率上都起作用。但这会带来一个问题：为了稳定低频，我们可能需要一个较大的电阻，但这个电阻在高频也会消耗大量增益，这显然不是我们想要的。

理想的解决方案是：让晶体管在高频时"看不见"这个稳定电阻 。这样高频增益得以保留，同时低频稳定性又能得到保障。实现这一目标的关键就是使用高通（High-Pass）结构 的电路。

让我们看一个典型电路：一个射频晶体管，其集电极通过一个射频扼流圈（RF Choke）接到偏置电压Vc。这个电路巧妙地同时实现了偏置和稳定：

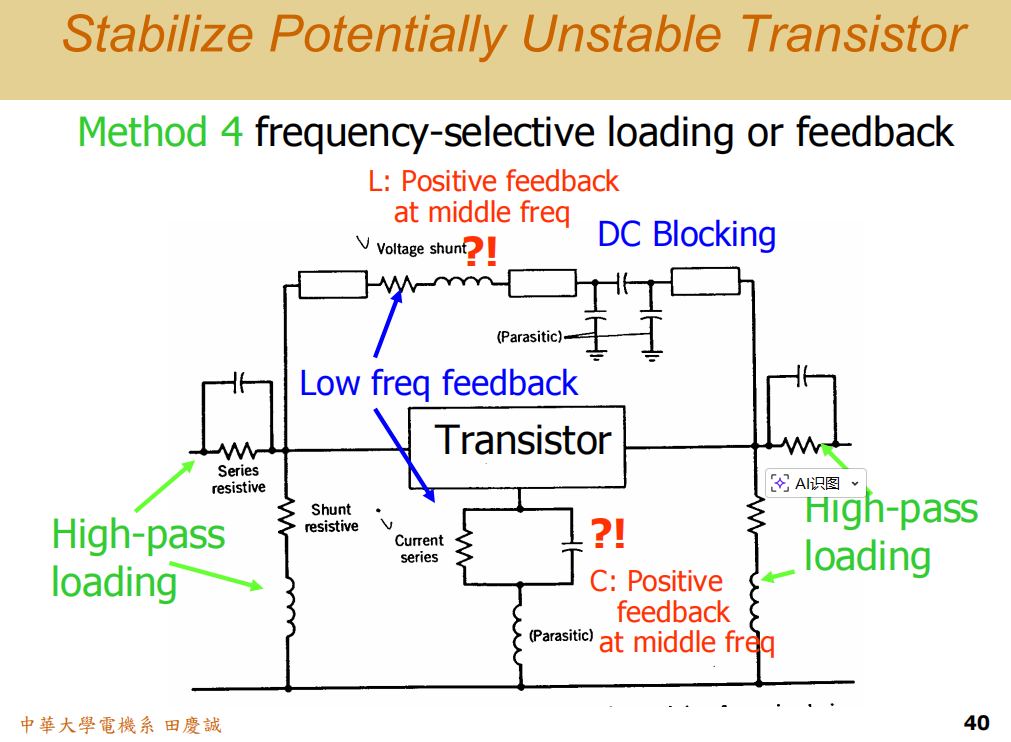
低频路径：在低频段，扼流圈的感抗很小，相当于短路。因此，输出信号会"看到"并流经偏置电阻到地，从而被衰减，保证了低频稳定性。
高频路径 ：在工作频段（如2.4GHz），扼流圈的感抗很大，相当于开路。因此，高频信号被阻隔，无法流向偏置电阻，从而几乎无损耗地输出，保证了高频增益。

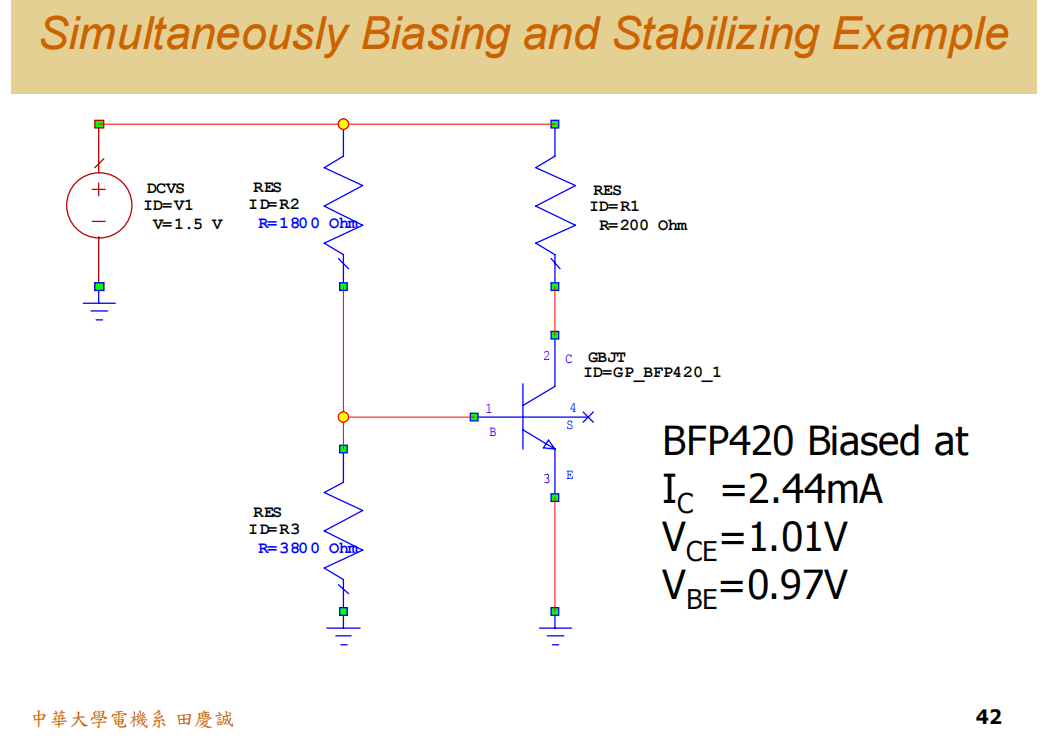
我们可以通过仿真来验证这一设计。以一个具体模型（如BFP420）为例，我们同时设计直流偏置点和稳定网络。

简单封装:

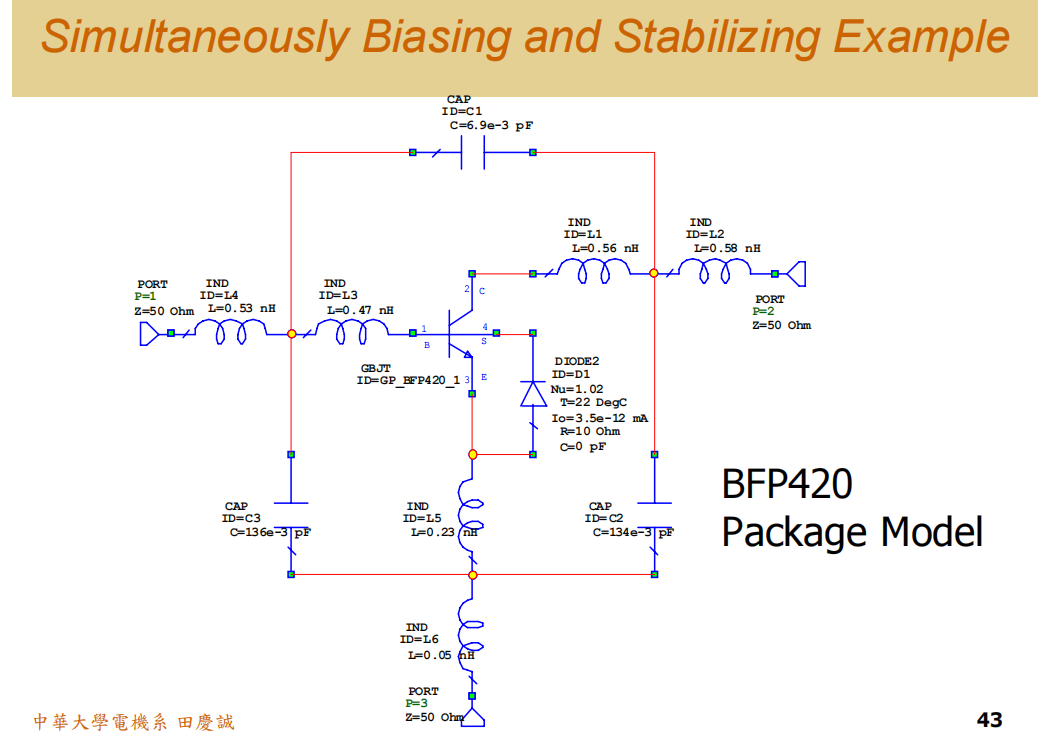
引入稳定网络:

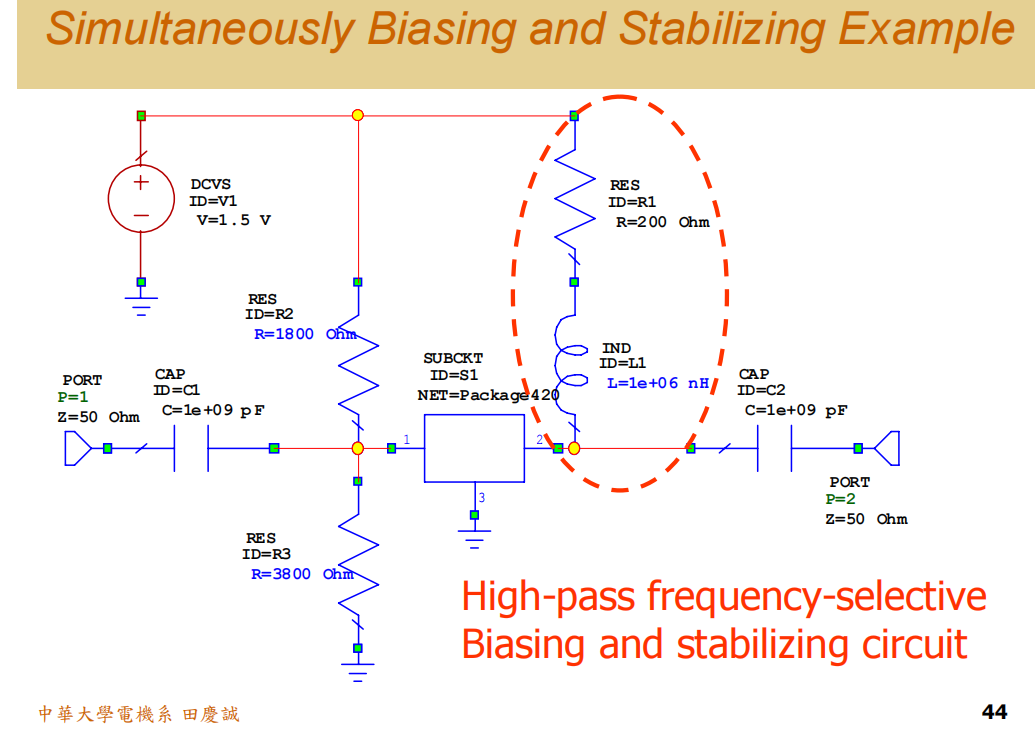
偏置设计 ：根据目标工作点（如VceVceVce=1.01V, IcIcIc=2.44mA）计算基极分压电阻。通常，流过分压电路的电流取集电极电流的1/10，这是一个常见的折中方案，既能稳定偏置点，又不会消耗过多静态功率。
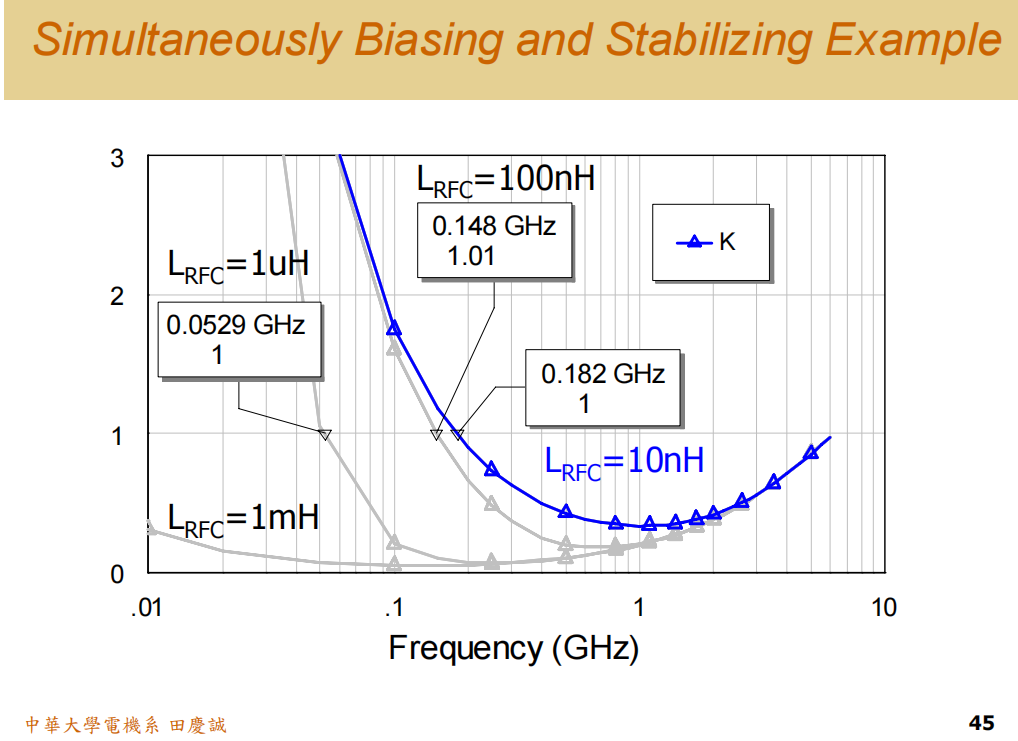
稳定性优化 ：关键在于调整扼流圈的电感值。
- 当电感值非常大时，连低频信号也无法通过，稳定电阻无法发挥作用，电路在全频段都可能不稳定（K因子 < 1）。
- 逐渐减小电感值 ，我们会发现低频段的K因子开始提升。电感值和稳定电阻共同构成了一个RL高通网络，其截止频率决定了从哪个频点开始电路变得稳定。我们可以通过调整电感值，精确控制电路在所需频率（如150MHz以下）实现稳定。
- 但是，电感值减小到一定程度后（例如10nH），对中高频段的稳定性提升会达到极限。这是因为在更高频率，扼流圈的感抗已经足够大，稳定电阻不再起作用。此时，如果该频段仍不稳定，就需要考虑其他方法，例如减小偏置电阻的阻值 （这可以通过调整偏置电压VcVcVc来实现），或者额外增加一个针对该频段的并联RC稳定网络 。

核心要点总结

电感值的选择 ：电感的大小没有绝对标准，它决定了稳定电路起作用的频率下限。对于工作频率（如2.4GHz），一个10nH的电感感抗很大，是良好的扼流圈；但对于低频（如240MHz），其感抗很小，稳定电阻得以接入。
稳定性的物理本质 ：让电路稳定的物理本质，是通过电阻消耗掉多余的增益。如果并联的电阻阻值过大（如400欧姆），分流作用就弱，消耗的增益少，稳定效果就差。因此，有时需要将电阻减小到合适的值（如80欧姆）才能有效提升K因子。

结论

将偏置电路与频率选择性稳定网络相结合，是射频设计中一个非常高效且常用的技巧。工程师需要理解其工作原理，并通过仿真反复调整元件参数（主要是电感值和电阻值），用最少的元件同时实现稳定的直流工作点、良好的高频性能以及可靠的全频带稳定性。