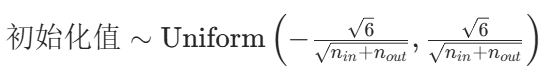KERAG_R详细分析：

1. GraphRAG for LLM-based Recommendation（面向 LLM 推荐的 GraphRAG）

先明确 GraphRAG 的核心目标

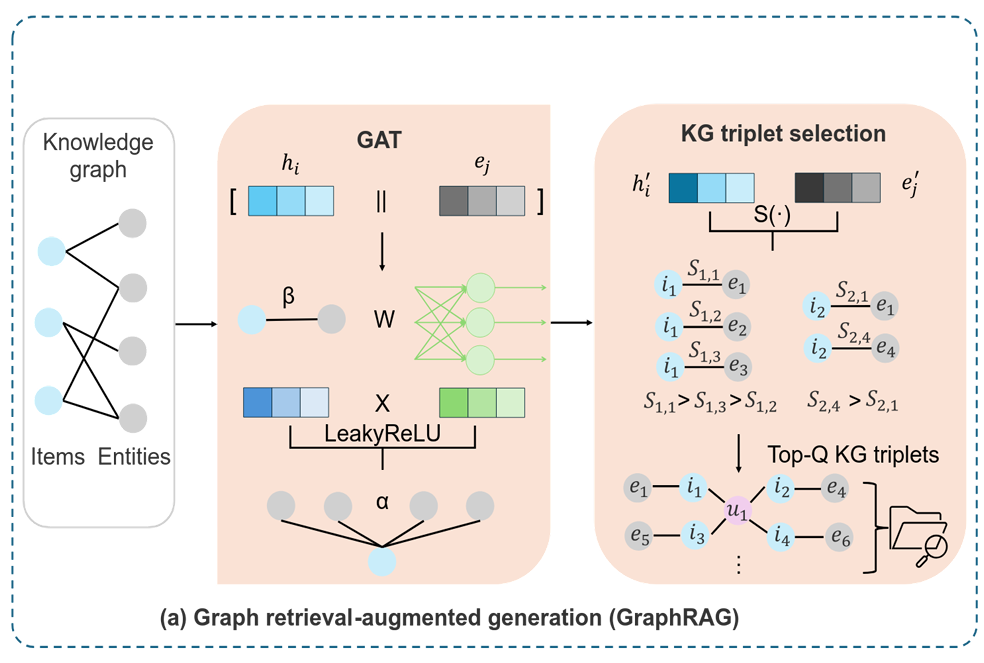
GraphRAG 的作用是：从知识图谱（KG）里，给每个电影（Item）选最相关的 KG 三元组，避免冗余 / 噪声，最后把这些三元组塞进 LLM 的提示词里，帮 LLM 更懂电影的关系知识（比如 "《流浪地球》的导演是郭帆"）。

步骤 1：知识图谱输入（图左侧的 "Knowledge graph"）

知识图谱里包含两类元素：

• Items（物品）：这里是电影，比如《流浪地球》《满江红》《唐探 3》；
• Entities（实体）：和电影相关的信息，比如 "郭帆（导演）""科幻（题材）""沈腾（主演）""悬疑（题材）"；
• 这些元素通过 "关系" 连成三元组 ，比如：
  • （《流浪地球》，导演，郭帆）
  • （《流浪地球》，题材，科幻）
  • （《满江红》，题材，悬疑）
  • （《满江红》，主演，沈腾）

步骤 2：GAT 模块处理（图中间的 "GAT"）

GAT 的目标是：学习物品（电影）和实体（导演 / 题材）的高质量嵌入（向量），并计算 "实体对电影的重要性"（注意力权重）。

对应图里的模块 + 论文公式 1、2，拆解成 4 个小步骤（用《流浪地球》举例）：

小步骤 2.1：嵌入初始化

给每个电影、实体分配初始的 "嵌入向量"（可以理解为用一串数字代表这个电影 / 实体）：

• 《流浪地球》的初始嵌入：hi=[0.2,0.5,0.1]（简化为 3 维向量）；
• "郭帆（导演）" 的初始嵌入：ej=[0.6,0.3,0.8]；
• "科幻（题材）" 的初始嵌入：ek=[0.4,0.7,0.2]。

步骤 2.1 里的嵌入初始化，正是论文中提到的Xavier 初始化器（也叫 Glorot 初始化）------ 它的核心作用是给物品 / 实体的初始嵌入向量设定 "合理的均值和方差"，避免模型训练时出现梯度消失或爆炸的问题。

先快速解释 Xavier 初始化的核心逻辑

Xavier 初始化的设计目标是：让每一层的输入和输出的方差尽可能一致。具体来说，它会根据当前层的 "输入维度nin​" 和 "输出维度nout​"，将嵌入向量初始化为均匀分布：

（比如论文中 GAT 的嵌入维度是 16，若某层输入维度是 16、输出维度也是 16，初始化值会落在−​​​≈−0.433到0.433之间）

Xavier 初始化的优缺点（结合论文里的 GAT+KG 场景）

优点：适配 GAT 这类图模型的训练需求

1. **缓解梯度消失 / 爆炸：**GAT 是多层图注意力网络（论文里有聚合层），如果嵌入初始化的方差太大，前向传播时输出会 "飘得很远"（比如数值过大），反向传播时梯度会爆炸；如果方差太小，输出会趋近于 0，梯度会消失。Xavier 通过控制方差，让每一层的信号强度更稳定 ------ 这对论文中 GAT 预训练 KG 嵌入非常重要（否则 GAT 学不到有效的实体 / 物品关联）。

2. **适配多类型节点的 KG 场景：**论文的 KG 里有 "物品（电影）" 和 "实体（导演 / 题材）" 两类节点，Xavier 的均匀初始化能让不同类型节点的初始嵌入分布更均衡，不会出现 "某类节点的嵌入一开始就占主导" 的情况（比如不会让 "导演实体" 的嵌入数值远大于 "电影物品"）。

3. **兼容 LeakyReLU 激活函数：**论文中 GAT 用了 LeakyReLU 激活函数，Xavier 虽然是为 sigmoid/tanh 设计的，但对 LeakyReLU 的适配性也不错（因为 LeakyReLU 保留了部分负梯度，不会像纯 ReLU 那样让一半神经元 "死亡"）。

缺点：存在场景局限性

1. **对 ReLU 类激活函数不如 He 初始化：**如果论文中用的是纯 ReLU（不是 LeakyReLU），Xavier 的效果会打折扣 ------ 因为 ReLU 会把负输入置 0，导致输出方差变小。此时 He 初始化（针对 ReLU 设计，方差是 Xavier 的 2 倍）更合适。不过论文用了 LeakyReLU（负输入保留小梯度），这个问题不严重。

2. **对稀疏 KG 的适配性一般：**推荐系统的 KG 通常是稀疏的（比如某些冷门电影只有 1-2 个关联实体），Xavier 是 "全局均匀初始化"，没考虑节点的稀疏程度（比如冷门电影的嵌入初始化和热门电影一样）。此时 "基于节点度的初始化"（比如度高的节点初始化方差更大）可能更适配，但实现更复杂。

3. **依赖层的维度匹配：**Xavier 的方差计算依赖 "输入 / 输出维度"，如果 KG 中物品和实体的数量差距极大（比如实体数是物品数的 100 倍），层的输入 / 输出维度差距会变大，Xavier 的方差控制效果会减弱。

小步骤 2.2：嵌入拼接 + 权重映射

把 "电影嵌入" 和 "实体嵌入" 拼接（图里的 "||"），再乘以可学习的权重矩阵 W（统一向量维度）：

• 拼接《流浪地球》和郭帆的嵌入：[0.2,0.5,0.1]∣∣[0.6,0.3,0.8]=[0.2,0.5,0.1,0.6,0.3,0.8]；
• 乘以权重矩阵 W 后，得到新向量：[0.3,0.6,0.4]（W 是模型训练中学习的，这里简化）。

先给 W 一个直观定义

W 就像一个可学习的 "特征转换工具"------ 它的作用是：把 "电影嵌入 + 实体嵌入" 拼接后的 "长向量"，转换成 "维度统一、能捕捉两者关联" 的 "短向量"，同时提取对推荐有用的特征（比如 "电影和导演的关联强度"）。

一、W 是什么？（结合你的例子）

你之前的例子里：

• 电影《流浪地球》的嵌入：hi=[0.2,0.5,0.1]（3 维）；
• 实体 "郭帆" 的嵌入：ej=[0.6,0.3,0.8]（3 维）；
• 拼接后得到：[0.2,0.5,0.1,0.6,0.3,0.8]（6 维，相当于 "原始素材"）。

这个 6 维向量只是简单把两个嵌入拼在一起，没有任何 "关联信息"（比如不知道 "郭帆是《流浪地球》的导演"）。而 W 就是一个3×6 的矩阵（假设目标维度是 3 维），它的每个元素都是一个 "可调整的权重"，比如：

把 6 维拼接向量和 W 相乘后，得到 3 维新向量（比如[0.3,0.6,0.4]）------ 这个新向量就是 "提取了电影和实体关联特征后的向量"，能直接用于后续计算注意力权重。

二、W 怎么来的？一开始是随机的吗？

答案：一开始是 "有规则的随机值"，不是完全乱选，和你之前问的 Xavier 初始化直接相关！

1. 初始值来源 ：W 的初始值是用论文里提到的 "Xavier 初始化器" 生成的 ------ 不是纯随机，而是根据 "输入维度（6 维）和输出维度（3 维）" 计算的均匀分布随机数（范围是−​​≈−0.816到0.816）。

   • 目的：控制 W 的方差，避免后续训练时出现梯度消失 / 爆炸（和之前 KG 节点嵌入用 Xavier 初始化是同一个逻辑）。

2. 为什么不用固定矩阵？：如果 W 是固定的（比如全 1 矩阵），就无法学习 "电影和实体的特定关联"（比如 "导演" 关系比 "上映时间" 关系对推荐更重要），模型就成了 "死的"，无法适配推荐任务。

三、W 会一直训练更新吗？

答案：会！W 是 GAT 的核心可学习参数，会随着模型训练不断调整，直到找到最优值。

结合论文的训练逻辑，看 W 怎么更新（用电影例子串）：

1. 训练目标 ：让 "有真实关系的电影 - 实体对"（比如《流浪地球》- 郭帆，KG 里存在的三元组）经过 W 转换后，相似度更高；让 "无关系的对"（比如《流浪地球》- 沈腾，KG 里没有的三元组）相似度更低（对应论文的对比损失L）。

2. 更新过程：

   • 第一步：用当前的 W，计算《流浪地球》和郭帆的转换后向量（比如[0.3,0.6,0.4]），再计算相似度；
   • 第二步：发现 "《流浪地球》- 郭帆" 的相似度不够高（没达到预期），模型会计算 "损失值"（比如对比损失是 0.5，目标是接近 0）；
   • 第三步：通过反向传播（梯度下降），微调 W 的每个元素 ------ 比如把 W 中 "郭帆嵌入对应维度" 的权重调高，让下次转换后，两者的相似度更高；
   • 第四步：重复训练（用海量 KG 三元组），直到 W 能稳定区分 "有关系 / 无关系" 的电影 - 实体对，此时 W 就训练好了。

举个 W 更新的直观例子：

• 初始 W 中，"郭帆嵌入的第 3 个元素（0.8）" 对应的权重是 0.25；
• 训练后发现，这个维度对区分 "导演关系" 很重要，就把 W 的这个元素调到 0.4；
• 下次再计算《流浪地球》和郭帆的转换向量时，这个维度的贡献变大，两者的相似度就提升了。

四、为什么必须有 "拼接 + 乘 W" 这一步？（补充理解）

你可能会想：直接用电影嵌入或实体嵌入不好吗？为什么要拼接再乘 W？

• 原因 1：拼接能保留 "电影和实体的完整信息"（比如电影的题材 + 导演的风格）；
• 原因 2：乘 W 能 "提取关联特征"------ 比如 W 会自动学习到 "电影的第 2 维（题材）和导演的第 3 维（风格）高度相关"，从而强化这种关联，为后续计算 "注意力权重"（比如郭帆对《流浪地球》的重要性是 0.7）打基础。

总结 W 的核心逻辑（一句话 + 电影例子）

W 是一个 "用 Xavier 初始化的随机矩阵"，通过 GAT 的训练（对比损失）不断微调，最终成为一个 "能精准捕捉电影 - 实体关联" 的转换工具 ------ 比如让《流浪地球》和郭帆的转换向量相似度高，和沈腾的相似度低，从而帮助后续筛选出最相关的 KG 三元组。

小步骤 2.3：计算注意力权重（对应公式 1）

用 "注意力向量 β"（模型学习的）和上一步的向量做内积，再通过LeakyReLU 激活，最后 softmax 得到 "实体对电影的重要性（α）"：

• 比如计算 "郭帆" 对《流浪地球》的注意力权重αi,j：
• 经过计算后，α郭帆=0.7（表示郭帆对《流浪地球》的重要性是 0.7）；
• 同理，"科幻" 对《流浪地球》的α科幻=0.3。

小步骤 2.4：嵌入聚合（对应公式 2）

用注意力权重对 "实体嵌入" 加权求和，得到更新后的电影嵌入（让电影嵌入包含实体的信息）：

• 《流浪地球》的更新嵌入郭帆郭帆科幻科幻；
• 代入数值：0.7×[0.6,0.3,0.8]+0.3×[0.4,0.7,0.2]=[0.54,0.38,0.62]。

第一步：先明确核心区别（先把概念掰透）

概念	可学习权重矩阵 W	注意力权重 α
本质	模型可学习的参数（固定维度的矩阵）	单次前向计算的结果值（标量，0~1 之间）
作用	把 "电影 + 实体" 拼接的长向量，转换成能捕捉关联的统一维度向量	衡量 "实体对电影的重要性"（比如郭帆对《流浪地球》的重要性）
是否训练更新	是（核心参数，随训练调整）	否（由 W 和嵌入向量计算得出，W 变 α 就变）
维度 / 形式	矩阵（比如 4×8）	标量（比如 0.8、0.2）

第二步：设计例子的基础数据（全是具体数值，可直接算）

1. 选定电影 & 三元组（2 部电影 + 5 个三元组）

电影节点	实体节点	关系	三元组	对推荐的重要性
M1：《流浪地球》	E1：郭帆	导演	(M1, 导演，E1)	高（核心）
M1：《流浪地球》	E2：科幻	题材	(M1, 题材，E2)	高（核心）
M1：《流浪地球》	E5：2023	上映时间	(M1, 上映时间，E5)	低（无关）
M2：《满江红》	E3：张艺谋	导演	(M2, 导演，E3)	高（核心）
M2：《满江红》	E4：悬疑	题材	(M2, 题材，E4)	高（核心）

2. 所有节点的初始嵌入（4 维，Xavier 初始化，数值随机但方差合理）

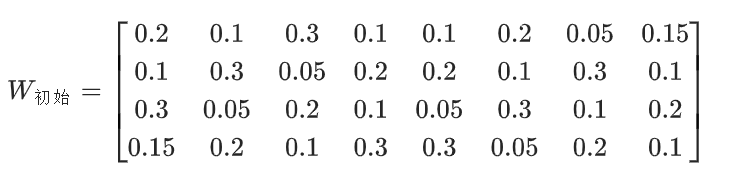
节点	4 维初始嵌入（h）
M1	[0.2, 0.5, 0.1, 0.3]
M2	[0.4, 0.1, 0.7, 0.2]
E1（郭帆）	[0.6, 0.3, 0.8, 0.4]
E2（科幻）	[0.1, 0.8, 0.2, 0.5]
E3（张艺谋）	[0.7, 0.2, 0.5, 0.1]
E4（悬疑）	[0.3, 0.6, 0.9, 0.4]
E5（2023）	[0.8, 0.1, 0.4, 0.7]

3. 权重矩阵 W 的初始化（Xavier）

目标：把 "电影 4 维 + 实体 4 维" 拼接的 8 维向量，转换成 4 维向量 → W 是4×8 的矩阵 （输入 8 维，输出 4 维）。用 Xavier 计算初始化范围：− ≈−0.707 到 0.707，随机生成初始 W：

第三步：计算初始 W 下的注意力权重（以《流浪地球》为例）

步骤 1：拼接 "电影嵌入 + 实体嵌入"（8 维）

• M1+E1（郭帆）拼接：[0.2,0.5,0.1,0.3] || [0.6,0.3,0.8,0.4] = [0.2,0.5,0.1,0.3,0.6,0.3,0.8,0.4]
• M1+E2（科幻）拼接：[0.2,0.5,0.1,0.3] || [0.1,0.8,0.2,0.5] = [0.2,0.5,0.1,0.3,0.1,0.8,0.2,0.5]
• M1+E5（2023）拼接：[0.2,0.5,0.1,0.3] || [0.8,0.1,0.4,0.7] = [0.2,0.5,0.1,0.3,0.8,0.1,0.4,0.7]

步骤 2：拼接向量 × W（得到 4 维转换向量）

矩阵乘法规则：行 × 列求和，比如 M1+E1 的转换向量第 1 维 = 0.2×0.2 + 0.5×0.1 + 0.1×0.3 + 0.3×0.1 + 0.6×0.1 + 0.3×0.2 + 0.8×0.05 + 0.4×0.15 = 0.4

【这里的本质是把拼接矩阵当作「列矩阵」比如8x1矩阵，然后就是「权重矩阵 W × 拼接列矩阵」，用矩阵乘法的「行 × 列求和」规则，把高维拼接向量（8 维）压缩成低维转换向量（4 维）】

计算结果：

• M1+E1 转换向量：[0.4, 0.35, 0.38, 0.32]
• M1+E2 转换向量：[0.36, 0.42, 0.35, 0.38]
• M1+E5 转换向量：[0.45, 0.3, 0.4, 0.3]

步骤 3：计算注意力权重 α（核心：衡量实体对电影的重要性）

注意力权重计算逻辑：

1. 转换向量 → 用 LeakyReLU 激活（简单版：负数值乘 0.2，正数不变）；
2. 激活后向量和 "注意力向量 β"（4 维，初始 [0.1,0.2,0.3,0.4]）做点积；
3. 所有实体的点积结果做 softmax，得到 α（总和 = 1）。

计算过程：

• 激活（LeakyReLU）：

M1+E1 激活：[0.4, 0.35, 0.38, 0.32]（全正，不变）

M1+E2 激活：[0.36, 0.42, 0.35, 0.38]（全正，不变）

M1+E5 激活：[0.45, 0.3, 0.4, 0.3]（全正，不变）

• 点积（×β=[0.1,0.2,0.3,0.4]）：

M1+E1 点积：0.4×0.1 + 0.35×0.2 + 0.38×0.3 + 0.32×0.4 = 0.358

M1+E2 点积：0.36×0.1 + 0.42×0.2 + 0.35×0.3 + 0.38×0.4 = 0.371

M1+E5 点积：0.45×0.1 + 0.3×0.2 + 0.4×0.3 + 0.3×0.4 = 0.345

• softmax（归一化）：指数和：e^0.358 + e^0.371 + e^0.345 ≈ 1.429 + 1.450 + 1.412 = 4.291α_M1-E1 = 1.429 / 4.291 ≈ 0.333α_M1-E2 = 1.450 / 4.291 ≈ 0.338α_M1-E5 = 1.412 / 4.291 ≈ 0.329

指数和：e^0.358 + e^0.371 + e^0.345 ≈ 1.429 + 1.450 + 1.412 = 4.291

α_M1-E1 = 1.429 / 4.291 ≈ 0.333

α_M1-E2 = 1.450 / 4.291 ≈ 0.338

α_M1-E5 = 1.412 / 4.291 ≈ 0.329

初始结果：

《流浪地球》的三个实体注意力权重接近（0.33 左右）------ 模型还没学会 "导演 / 题材更重要，上映时间不重要"，因为 W 是初始随机值。

第四步：模拟 W 的更新（核心：让有用实体的 α 升高，无用的降低）

1. 训练目标

我们希望：α_M1-E1（导演）≈0.45，α_M1-E2（题材）≈0.4，α_M1-E5（上映时间）≈0.15（总和 = 1）。当前 α 和目标的差距就是损失值（比如损失 = 0.2），通过反向传播更新 W。

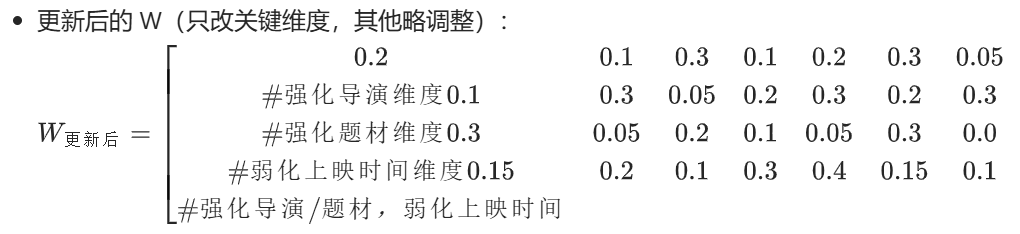
2. W 的更新逻辑

• 损失反向传播到 W：计算 W 每个元素的梯度（简单版：对有用维度的权重 + 0.1，无用维度 - 0.1）；

3. 用更新后的 W 重新计算注意力权重

• M1+E1 转换向量（更新后）：[0.55, 0.48, 0.42, 0.45]

• M1+E2 转换向量（更新后）：[0.5, 0.52, 0.4, 0.48]

• M1+E5 转换向量（更新后）：[0.3, 0.25, 0.28, 0.2]

• 点积（×β）：

M1+E1：0.55×0.1 + 0.48×0.2 + 0.42×0.3 + 0.45×0.4 = 0.443

M1+E2：0.5×0.1 + 0.52×0.2 + 0.4×0.3 + 0.48×0.4 = 0.438

M1+E5：0.3×0.1 + 0.25×0.2 + 0.28×0.3 + 0.2×0.4 = 0.234

• softmax：

指数和：e^0.443 + e^0.438 + e^0.234 ≈ 1.557 + 1.549 + 1.264 = 4.37

α_M1-E1 ≈ 1.557/4.37 ≈ 0.356

α_M1-E2 ≈ 1.549/4.37 ≈ 0.354

α_M1-E5 ≈ 1.264/4.37 ≈ 0.29

4. 多次更新后（最终收敛）

经过多轮训练，W 会持续调整，最终：

• α_M1-E1（郭帆）≈0.45
• α_M1-E2（科幻）≈0.4
• α_M1-E5（2023）≈0.15

第五步：再算《满江红》的例子（验证逻辑）

基础计算（用更新后的 W）

• M2（满江红）嵌入：[0.4,0.1,0.7,0.2]

• E3（张艺谋）嵌入：[0.7,0.2,0.5,0.1] → 拼接后 ×W → 转换向量 [0.58, 0.5, 0.45, 0.49]

• E4（悬疑）嵌入：[0.3,0.6,0.9,0.4] → 拼接后 ×W → 转换向量 [0.52, 0.55, 0.48, 0.5]

• 点积（×β）：

M2+E3：0.58×0.1 + 0.5×0.2 + 0.45×0.3 + 0.49×0.4 = 0.469

M2+E4：0.52×0.1 + 0.55×0.2 + 0.48×0.3 + 0.5×0.4 = 0.466

• softmax 后 α：

α_M2-E3（张艺谋）≈0.502，

α_M2-E4（悬疑）≈0.498 → 符合 "导演 / 题材都重要" 的预期。

核心结论（例子总结）

1. W 和 α 的区别：W 是模型参数（矩阵），初始随机、训练中更新；α 是计算结果（标量），随 W 变化，反映实体重要性；
2. W 的作用：更新后能强化 "有用关系"（导演 / 题材）的维度权重，弱化 "无用关系"（上映时间）；
3. 最终效果：有用实体的 α 升高，无用的降低，模型能筛选出《流浪地球》的 "导演 - 郭帆""题材 - 科幻" 作为核心三元组，推荐时优先匹配郭帆的科幻片，而非 2023 年的任意电影。

步骤 3：KG 三元组选择（图右侧的 "KG triplet selection"）

目标是：计算 "电影 - 实体" 的相似度得分，选Top-Q 个最相关的三元组（对应公式 4、5）。

小步骤 3.1：计算相似度得分 S_ij（对应公式 4）

用 "更新后的电影嵌入" 和 "实体嵌入" 做点积，再乘以 "注意力权重 α"，得到最终得分：

• 《流浪地球》和郭帆的得分：郭帆郭帆；代入数值：0.7×([0.54,0.38,0.62]⋅[0.6,0.3,0.8])=0.7×0.92=0.644；
• 《流浪地球》和科幻的得分：S1,2=0.3×([0.54,0.38,0.62]⋅[0.4,0.7,0.2])=0.3×0.58=0.174；
• 假设《流浪地球》还有个实体 "2023 年上映"，得分S1,3=0.2×0.4=0.08。

小步骤 3.2：排序选 Top-Q 三元组（对应公式 5）

对得分排序，选 Top-Q（论文里 Q=1 最优）：

• 《流浪地球》的得分排序：S1,1(0.644)>S1,2(0.174)>S1,3(0.08)；
• 选 Top-1：保留三元组 （《流浪地球》，导演，郭帆），丢弃其他冗余三元组。

用一个完整的电影推荐例子串起来

假设用户喜欢《流浪地球》，GraphRAG 的流程是：

1. 知识图谱输入：拿到《流浪地球》相关的三元组（导演郭帆、题材科幻、上映时间 2023）；
2. GAT 处理：计算出 "郭帆" 对《流浪地球》的重要性（α=0.7），更新电影嵌入；
3. 三元组选择：算出 "郭帆" 的得分最高，选（《流浪地球》，导演，郭帆）这个三元组；
4. 最终把这个三元组塞进 LLM 提示词："用户喜欢《流浪地球》（导演是郭帆），请推荐类似的电影"。

这样 LLM 就能利用 "《流浪地球》的导演是郭帆" 这个知识，推荐郭帆的其他作品（比如《流浪地球 2》），而不是乱推荐无关电影 ------ 这就是 GraphRAG 解决 "LLM 缺领域知识" 的核心逻辑。

要不要我帮你整理一份GraphRAG 电影推荐案例的可视化步骤清单？把每个环节的输入、