快慢指针问题

1. 环形链表

https://leetcode.cn/problems/linked-list-cycle/description/

这个问题如果直接遍历链表，走一圈看有没有出现过的地址，需要把所有地址记录下，这样时空复杂度都是O(n)，现在想要更好的空间复杂度。

考虑使用两个指针，一个快一个慢，快指针的速度是慢指针的两倍，它们同向行驶，这样，如果链表有环，这俩指针一定能够在某个位置相遇(差值是1的整数倍，n步走完一定能够构造出环长的整数倍)

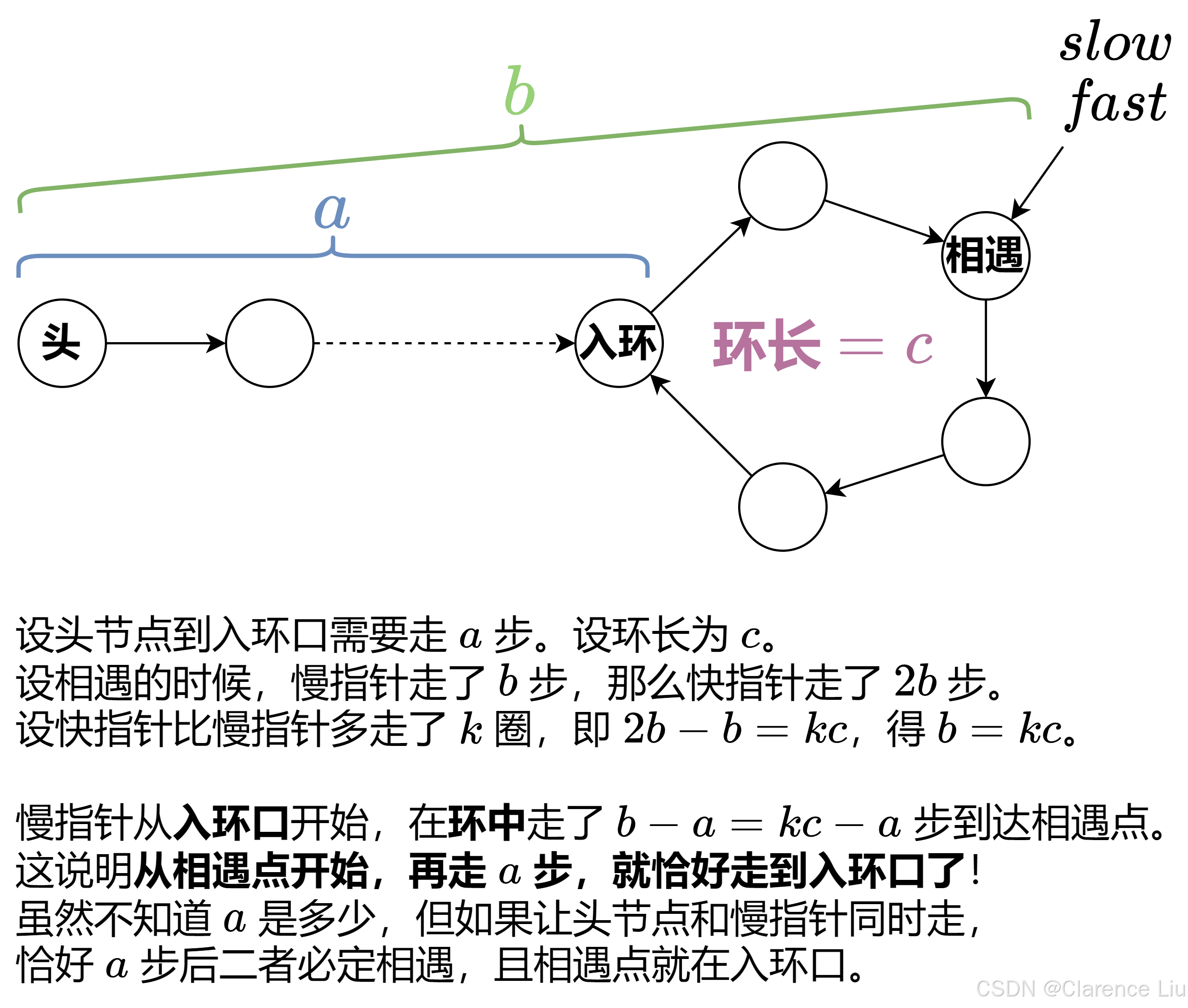
上面这个图比较详细

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != NULL && slow != NULL && fast -> next != NULL) {
            fast = fast -> next -> next;
            slow = slow -> next;
            if(fast == slow) {
                return true;
            }
        }
        return false;
    }
};

2. 环形链表2

https://leetcode.cn/problems/linked-list-cycle-ii/

在第一个问题里面，我们知道了可以用一个速度为 2 2 2的快指针和一个速度为 1 1 1的慢指针来判断链表是否有环。现在这个问题，让我们找入环点是哪一个，还是看下面这个图

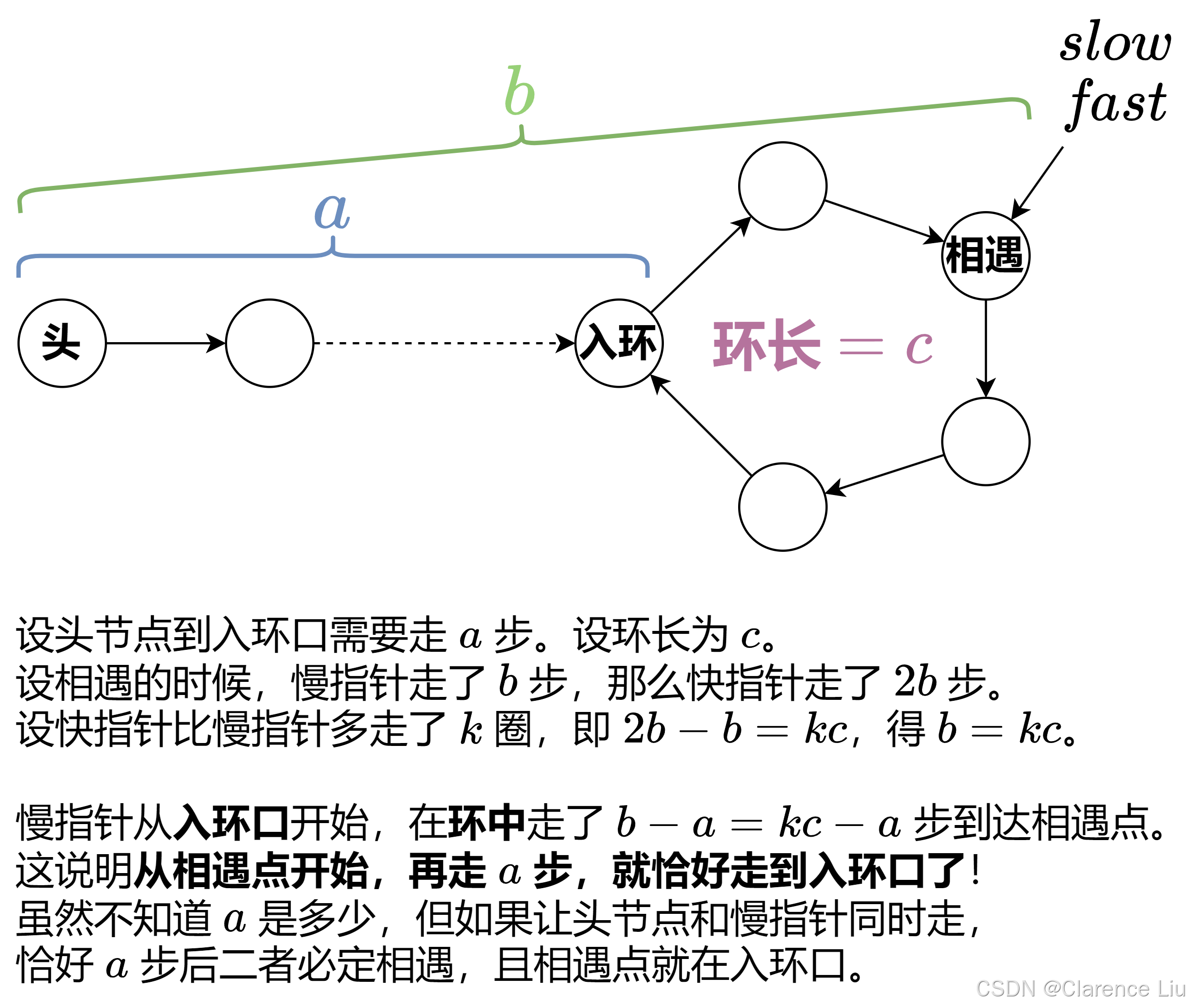
这里设 b b b是慢指针跟快指针相遇的时候，它走的步数，那么快指针因为速度是它的两倍，所以走了 2 b 2b 2b步，所以 2 b − b 2b-b 2b−b就是快指针比慢指针多走了多少圈，这里设为 k k k圈，所以 2 b − b = b = k c 2b-b=b=kc 2b−b=b=kc。对于慢指针来说，走到相遇点的时候，有 b − a = k c − a b-a=kc-a b−a=kc−a，那么在相遇点，再走a步就能走到入环点了，这跟头节点到入环点的距离刚好相等，这个时候，如果把头节点放上一个跟慢指针一样速度的指针，让慢指针从相遇点继续走。正好能跟头节点的指针相遇。这样就找到了入环点

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(slow != NULL && fast != NULL && fast -> next != NULL) {
            if(slow == NULL || fast -> next == NULL) {
                return NULL;
            }
            slow = slow -> next;
            fast = fast -> next -> next;
            if(fast == slow) {
                fast = head;
                while(fast != slow) {
                    fast = fast -> next;
                    slow = slow -> next;
                }
                return fast;
            }
        }
        return NULL;
    }
};

快慢指针问题

目录

1. 环形链表

2. 环形链表2