1. 前言
想要传递给下层调用栈的信息 / 想要从上层调用栈获取的信息,需要存在于递归方法参数中,或将其定义为全局变量。如果定义为全局变量则必须手动回溯,如果定义为方法参数且为基本数据类型或 String 则调用栈会帮我们自动回溯,引用类型还是要手动回溯(否则必须在方法中创建副本)。优先定义全局变量。
递归方法的返回值是想要传递给上层调用栈的信息。
先想清楚重复的子问题是什么。
有时书写递归代码需要转变思考模式,不是考虑怎样一步一步地解决这个问题,而是在递归方法体中定义出解决子问题的模式,让递归的函数遵守这个模式完成调用和返回。
牢记递归的本质是 dfs,即深度遍历。
递归出口的返回值是最后一个调用栈返回给上层调用栈的,方法最后的返回值是其他调用栈返回给上层调用栈的。
谈到二叉搜索树想中序遍历。谈到路径想前序遍历。
2. 经典递归问题
面试题 08.06. 汉诺塔问题 - 力扣(LeetCode)
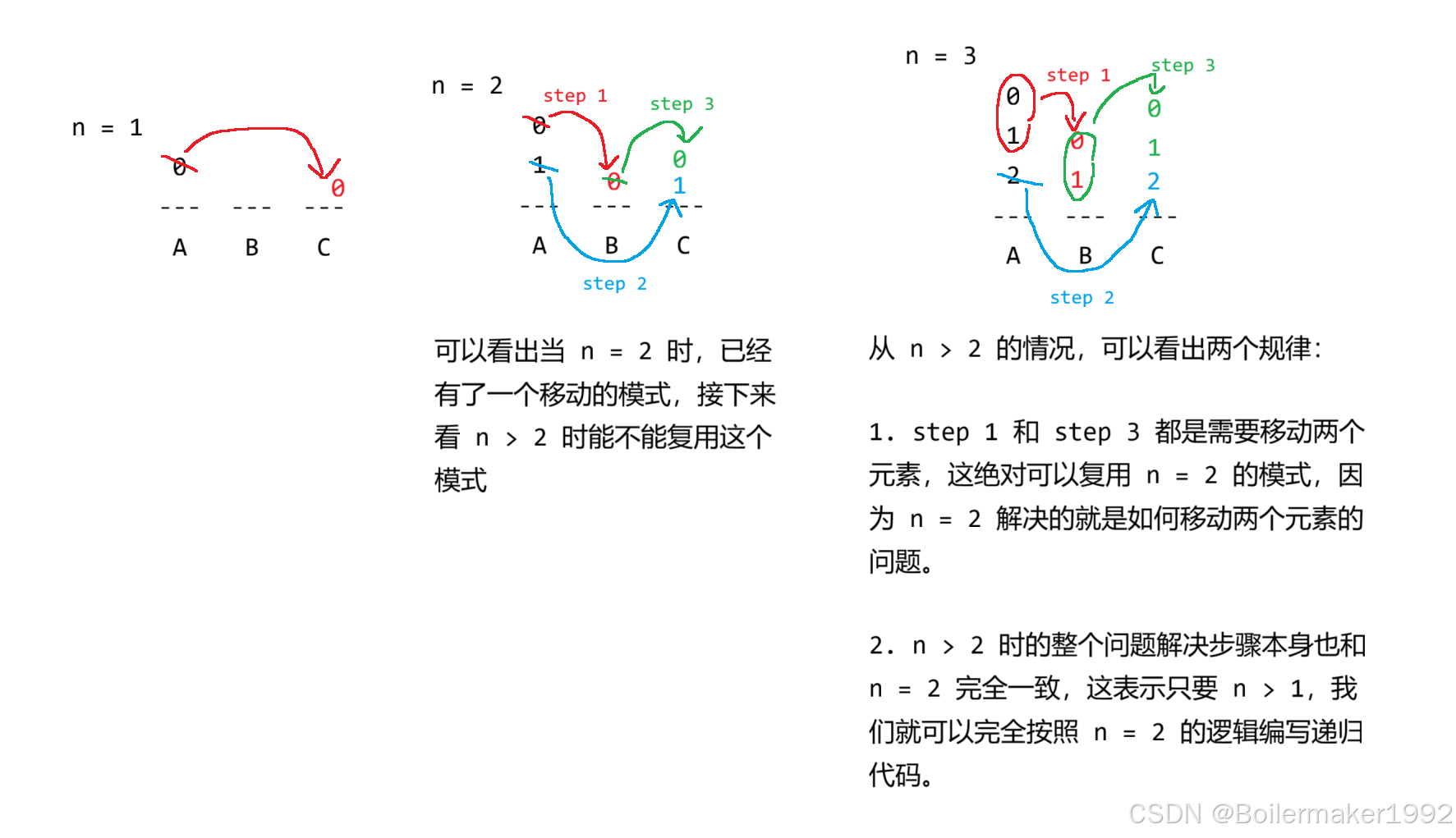
**子问题:**移动两个圆盘。
**方法签名:**void dfs(source, auxiliary, target, n)
这表示,从 source,借助 auxiliary,移动到 target。n 为 source 中的元素数量,用于使递归找到出口。
这道题一般的思路是,在两个链表上分别定义指针,比较指向的节点的值,小的节点入结果集,指向小节点的指针向后移动。现在若想使用递归解决问题,这个比较模式仍需保留。
**子问题:**合并两个有序链表。
java
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
if (list1 == null) {
return list2;
}
if (list2 == null) {
return list1;
}
if (list1.val < list2.val) {
list1.next = mergeTwoLists(list1.next, list2);
return list1;
} else {
list2.next = mergeTwoLists(list1, list2.next);
return list2;
}
}
}相同类型的题目还有:206. 反转链表 - 力扣(LeetCode)、24. 两两交换链表中的节点 - 力扣(LeetCode)
这道题如果直接递归 n 次一定会超时,更好的解法是模拟二叉树,这样就只需要递归 logn 次。
java
class Solution {
public double myPow(double x, int n) {
return n < 0 ? (1 / myPowPositive(x, -n)) : myPowPositive(x, n);
}
private double myPowPositive(double x, int n) {
if (n == 0) { // 最后一个调用栈
return 1.0;
}
double half = myPowPositive(x, n / 2);
x = n % 2 == 0 ? half * half : half * half * x;
return x;
}
}3. 二叉树的递归
129. 求根节点到叶节点数字之和 - 力扣(LeetCode)
从根节点开始,一路向下走到叶子节点,在这个过程中计算路径数字,再将返回值传递给父节点。
java
class Solution {
public int sumNumbers(TreeNode root) {
return sum(root, 0);
}
public int sum(TreeNode root, int preSum) {
int curSum = preSum * 10 + root.val;
if (root.left == null && root.right == null) {
return curSum;
}
int ret = 0;
if (root.left != null) {
ret += sum(root.left, curSum);
}
if (root.right != null) {
ret += sum(root.right, curSum);
}
return ret;
}
}
java
class Solution {
public TreeNode pruneTree(TreeNode root) {
prune(root);
// 特殊讨论只有一个节点且为 0 的情况
if (root.left == null && root.right == null && root.val == 0) {
return null;
}
return root;
}
private boolean prune(TreeNode root) {
if (root == null) {
return true;
}
boolean allZeroLeft = prune(root.left);
boolean allZeroRight = prune(root.right);
// 剪枝
if (allZeroLeft) {
root.left = null;
}
if (allZeroRight) {
root.right = null;
}
// 返回给上层调用栈
if (root.val == 0 && allZeroLeft && allZeroRight) {
return true;
}
return false;
}
}或使用更简单的写法:
java
class Solution {
public TreeNode pruneTree(TreeNode root) {
if (root == null) {
return null;
}
root.left = pruneTree(root.left);
root.right = pruneTree(root.right);
if (root.left == null && root.right == null && root.val == 0) {
root = null;
}
return root;
}
}BST 的性质是,其中序遍历的结果是严格升序的。
因此在这里需要对 root 做中序遍历,对于每一个调用栈,我们都需要用此处 root 的值与其前一个调用栈的 root 值做比较。这样就可以模拟出直接对 root 做中序遍历,再将遍历结果放入数组,比较数组是否有序的过程。
不剪枝的写法:
java
class Solution {
public long tempVal = Long.MIN_VALUE; // 记录上一个调用栈的值
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
boolean isValidLeft = isValidBST(root.left);
if (root.val <= tempVal) {
return false;
}
tempVal = root.val;
// 此时即使左树已返回 false,还是要继续递归右树,这没有必要
boolean isValidRight = isValidBST(root.right);
return isValidLeft && isValidRight;
}
}剪枝的写法:
java
class Solution {
public long tempVal = Long.MIN_VALUE; // 记录上一个调用栈的值
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
boolean isValidLeft = isValidBST(root.left);
if (!isValidLeft || root.val <= tempVal) { // 剪枝
return false;
}
tempVal = root.val;
boolean isValidRight = isValidBST(root.right);
return isValidRight;
}
}相同类型的题目还有:230. 二叉搜索树中第 K 小的元素 - 力扣(LeetCode)
回溯时要注意,必须在确保下一个调用栈能顺利在路径上添加元素的前提下再回溯,假如下一个调用栈还没执行到添加就返回了,那么回溯肯定会出问题。
java
class Solution {
List<String> ret;
List<Integer> path;
public List<String> binaryTreePaths(TreeNode root) {
ret = new ArrayList<>();
path = new ArrayList<>();
findPaths(root);
return ret;
}
private void findPaths(TreeNode root) {
path.add(root.val);
if (root.left == null && root.right == null) { // 叶子节点
StringBuilder builder = new StringBuilder();
for (int num : path) {
builder.append("->").append(num);
}
ret.add(builder.substring(2).toString());
return;
}
if (root.left != null) {
findPaths(root.left);
path.remove(path.size() - 1); // 回溯
}
if (root.right != null) {
findPaths(root.right);
path.remove(path.size() - 1); // 回溯
}
}
}4. 综合练习
注意对于引用类型一定要添加副本到结果集,而不是直接使用原引用,使用原引用的话这个值肯定会被一直修改。
java
class Solution {
List<List<Integer>> ret;
List<Integer> path;
boolean[] used;
public List<List<Integer>> permute(int[] nums) {
ret = new ArrayList();
path = new ArrayList();
used = new boolean[nums.length];
dfs(nums);
return ret;
}
private void dfs(int[] nums) {
if (nums.length == path.size()) {
ret.add(new ArrayList(path)); // 必须添加副本
return;
}
for (int i = 0; i < nums.length; i++) {
if (!used[i]) {
used[i] = true;
path.add(nums[i]);
dfs(nums);
// 回溯
path.remove(path.size() - 1);
used[i] = false;
}
}
}
}1863. 找出所有子集的异或总和再求和 - 力扣(LeetCode)

java
class Solution {
int ret;
int path;
public int subsetXORSum(int[] nums) {
dfs(nums, 0);
return ret;
}
private void dfs(int[] nums, int cur) {
while (cur < nums.length) {
path ^= nums[cur];
ret += path;
dfs(nums, cur + 1); // 递归下一个位置,保证不会选到重复元素
path ^= nums[cur];
cur++;
}
}
}
java
class Solution {
List<List<Integer>> ret;
List<Integer> path;
boolean[] used;
public List<List<Integer>> permuteUnique(int[] nums) {
ret = new ArrayList<>();
path = new ArrayList<>();
used = new boolean[nums.length];
dfs(nums);
return ret;
}
private void dfs(int[] nums) {
if (path.size() == nums.length) {
ret.add(new ArrayList(path));
return;
}
// set 是需要记录在调用栈中的信息,表示不可选元素集合
Set<Integer> set = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
if (!used[i]) { // 该下标(i)的元素未在 path 中被选到
used[i] = true;
if (!set.contains(nums[i])) { // 该元素可选(未与之前重复)
set.add(nums[i]);
path.add(nums[i]);
dfs(nums);
path.remove(path.size() - 1);
}
used[i] = false;
}
}
}
}
java
class Solution {
List<String> ret;
char[] path;
String[] LETTER_MAP = {
"", "", "abc", "def", "ghi", "jkl",
"mno", "pqrs", "tuv", "wxyz"
};
public List<String> letterCombinations(String digits) {
char[] digitsArr = digits.toCharArray();
ret = new ArrayList<>();
path = new char[digitsArr.length];
dfs(digitsArr, 0);
return ret;
}
private void dfs(char[] digitsArr, int curDigit) {
if (curDigit >= digitsArr.length) {
ret.add(new String(path));
return;
}
char[] group = LETTER_MAP[digitsArr[curDigit] - '0'].toCharArray();
for (int i = 0; i < group.length; i++) {
path[curDigit] = group[i];
dfs(digitsArr, curDigit + 1);
// 无需显式回溯,因为下次循环会覆盖
}
}
}一个合法的 path,其从左向右遍历,左括号的数量应始终大于等于右括号的数量,并在最后保持相等。
根据这个原则,当递归右括号时,需要保证此时剩下的左括号数量大于右括号的数量,不满足此条件时无需递归右括号,即剪枝。无需使用 stack 来维护 path 的合法性,只要满足以上条件即可。
java
class Solution {
List<String> ret;
char[] path;
public List<String> generateParenthesis(int n) {
ret = new ArrayList<>();
path = new char[n * 2];
dfs(n, n);
return ret;
}
// left:剩下的左括号个数
// right:剩下的右括号个数
private void dfs(int left, int right) {
if (left == 0 && right == 0) {
ret.add(String.valueOf(path));
return;
}
int target = path.length - left - right;
if (left > 0) {
path[target] = '(';
dfs(left - 1, right);
// 无需显式回溯
}
if (right > left) {
path[target] = ')';
dfs(left, right - 1);
// 无需显式回溯
}
}
}