项目组实习生长期招聘,中国铁道科学研究院测量系统开发团队,希望你有导航或测绘专业背景,有c/c++开发经验。有意者请邮箱联系我: chenshiming199510@163.com
背景
车辆在运动条件下想要实现姿态初始对准,常见的做法是利用GNSS(双天线更准确)与IMU的轨迹相似性实现该过程。但是如果没有卫星信号,这种方法显然是失效的。一种可靠的方案是采用里程计与IMU数据做组合,从而实现姿态初始对准。当然,前提是采用光纤级别的惯导才有可能实现。下面给出算法有效的前提:
- 已知纬度信息
- 光纤级别及以上的IMU
- 里程计与IMU准确同步
本次工作主要参考论文为"严恭敏,秦永元,卫育新,等.一种适用于SINS动基座初始对准的新算法[J].系统工程与电子技术,2009,31(03):634-637.",参考的其他论文如下:
-
In-motion alignment for a velocity-aided SINS with latitude uncertainty:在动基座下进行初始对准。针对需要精确姿态信息而位置信息不容易获得或不一定需要的情况,如姿态航向参考系统,本文提出了一种在地理纬度不确定情况下的带下惯性导航系统(SINS)速度辅助运动对准方案。在粗对准阶段,设计了一种基于积分速度平滑的重力视运动重建方法,以粗略确定姿态和纬度信息。然后,SINS/速度积分导航方法利用记录的数据完成精细对准。由于采用了精心设计的反向跟踪导航策略,存储空间和计算负荷都降低到了普通导航计算机可以承受的程度。我们进行了九次船舶测试,结果表明,所提出的方法可以在运动环境中以 0.04° 的精度对准方位角,与已知位置的正常运动中对准的精度相同。
-
基于里程计辅助的SINS动基座初始对准方法-系统工程与电子技术-2013
-
纬度未知条件下捷联惯导系统晃动基座的初始对准-王跃钢-严恭敏程序Whaba方法
-
最优估计对准(OBA)低成本 MEMS-INS/GNSS 组合导航动基座初始对准技术研究-硕士毕业论文(利用GNSS信息来对准)
-
车载捷联惯导系统动基座初始对准方法研究-南京理工大学-博士论文
算法原理
严恭敏等[6] 首先提出了静基座条件下的纬度估计方法,利用地球自转角速度矢量和重力矢量之间的几何关系,即可获得纬度信息的解析解:
L = arcsin f b ⋅ ω i e b ∥ f b ∥ ⋅ ∥ ω i e b ∥ L = \arcsin \frac{{{{\bf{f}}^b} \cdot {\bf{\omega }}{ie}^b}}{{\left\| {{{\bf{f}}^b}} \right\| \cdot \left\| {{\bf{\omega }}{ie}^b} \right\|}} L=arcsin∥fb∥⋅ ωieb fb⋅ωieb
利用里程计测的速度作为修正进行动基座初对准。参考《基于惯性参考系的动基座初始对准与定位导航 》《一种适用于 SINS 动基座初始对准的新算法 》两篇论文,详细推导见论文。
设定初始时刻惯性系为 F i 0 \mathscr {F}{i_0} Fi0,初始时刻的本体系为 F i b 0 \mathscr {F}{i_{b0}} Fib0,本体系为 F b \mathscr {F}{b} Fb,当地水平坐标系为 F n \mathscr {F}{n} Fn,当前时刻本体系至地理坐标系的姿态矩阵为 C b n C_b^n Cbn,则存在如下关系
C b n = C i 0 n C i b 0 i 0 C b i b 0 C_b^n = C_{i_{0}}^nC_{i_{b_0}}^{i_{0}}C_{b}^{i_{b_0}} Cbn=Ci0nCib0i0Cbib0
利用陀螺输出的角速度信息,通过捷联惯导姿态更新算法可以更新计算 C b i b 0 C_{b}^{i_{b_0}} Cbib0, C i 0 n C_{i_{0}}^n Ci0n可根据初始纬度和地球自转进行计算。
C ˙ b i b 0 = C b i b 0 ( ω i b b ) × \dot C_b^{{i_{{b_0}}}}= C_b^{{i_{{b_0}}}}(\omega^b_{ib})\times C˙bib0=Cbib0(ωibb)×
式中 ( ω i b b ) × (\omega^b_{ib})\times (ωibb)× 表示由 ω i b b \omega^b_{ib} ωibb构成的反对称矩阵,可设定初始矩阵为单位矩阵。
C b i b 0 ( v ˙ b + ω i b b × v b + ω i e b × v b − f s f b ) ≈ C i 0 i b 0 C n 0 i 0 g n C_b^{i_{b0}}({\dot v^b} + \omega {ib}^b \times {v^b} + \omega {ie}^b \times {v^b} - f{sf}^b{\rm{) \approx }}C{{i_0}}^{{i_{b0}}}C_{n_0}^{{i_0}}{g^n} Cbib0(v˙b+ωibb×vb+ωieb×vb−fsfb)≈Ci0ib0Cn0i0gn
式中 v ˙ b \dot v^b v˙b与 v b v^b vb均由里程计得到。为了降低速度求微分计算而导致噪声较大的影响,对上式进行积分,有
v t i b 0 = C i 0 i b 0 u t i 0 v_t^{{i_{{b0}}}} = C{{i_0}}^{{i_{b0}}}u_t^{{i_0}} vtib0=Ci0ib0uti0
式中
v t i b 0 = ∫ t 0 t C b i b 0 ( v ˙ b + ω i b b × v b − f b ) d t , u t i 0 = ∫ t 0 t C n 0 i b 0 g n d t v_t^{{i_{{b0}}}} = \int{{t_0}}^t {C_b^{{i_{b0}}}({{\dot v}^b} + \omega {ib}^b \times {v^b} - {f^b})dt} ,\;\;\;u_t^{{i_0}} = \int{{t_0}}^t {C_{{n_0}}^{{i_{b0}}}{g^n}dt} vtib0=∫t0tCbib0(v˙b+ωibb×vb−fb)dt,uti0=∫t0tCn0ib0gndt
可采用双矢量解析式初始对准计算,或者采用最优姿态估计方法。构建Wahba损失方程如下
L ( C b i b 0 ) = ∑ k = 1 n ( v t i b 0 − C i 0 i b 0 u t i 0 ) L(C_b^{i_{b0}})=\sum\limits_{k=1}^{n} {(v_t^{{i_{{b0}}}} - C{{i_0}}^{{i_{b0}}}u_t^{{i_0}})} L(Cbib0)=k=1∑n(vtib0−Ci0ib0uti0)
求损失方程极小矩阵可以采用QUEST算法,可迭代更新 C b i b 0 C_b^{i_{b0}} Cbib0矩阵,当计算值逐渐稳定,即完成了航向角的对准。然后将 C b i b 0 C_b^{i_{b0}} Cbib0带入至上式求解当前的姿态矩阵 C b n C_b^{n} Cbn。若假设纬度误差最大为150km,由150km的纬度误差引起的地球自转速度投影误差为0.35°/h,与陀螺的漂移在同一个量级。由此可知,在系统初始时刻只需要输入大致的纬度信息即可,对动态对准精度的影响较小。
效果评估
实验条件:项目组将IMU安装在轨道列车上,在专用实验线路开展了相关测试。由于列车在绕圈行驶,所以能看出来摇头角在周期性变化。
对初始对准的精度进行了评估。系统在列车正常行驶的条件下进行姿态初始对准,初始行车速度为72 km/h。初始对准精度评估结果如图 所示。由图 (a)可知,航向角测量值在刚开始时误差较大,随时间逐渐与参考值相近。由图 (b)可知,航向角误差在刚开始的500 s内变化较大,后面逐渐稳定;在516 s后,航向角误差稳定在1°以内;水平姿态角误差在20 s内迅速减小至0.1°以内。
在惯性导航理论中,航向角对准的理论精度由东向陀螺仪零偏决定,通常表示为

若东向陀螺零偏为0.2°/h,那么航向角的对准精度为0.98°左右。这表明了对准姿态精度已接近理论值。
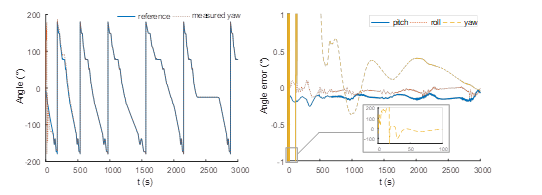
图 初始对准精度评估 (a) 摇头角测量值与参考值对比;(b) 三轴角度误差随时间的变化
小结
本文不求甚解的复现了严老师的论文中的内容。发现这种方案并不能达到一个理想的效果,主要问题在于收敛速度太慢,期望后续能够有所改进。
matlab核心代码如下,希望对你有所帮助。
matlab
lat0 = P0(1); lon0 = P0(2);
eth = ethinit(P0);
gn = [0; 0; -eth.g0];
% C_n0_e = [-sin(lat0), cos(lat0), 0;
% -sin(lat0)*cos(lon0), -sin(lat0)*sin(lon0), cos(lat0);
% cos(lat0)*cos(lon0), cos(lat0)*sin(lon0), sin(lat0)];
omega_ie = 2*pi/24/3600;
t = 0;
t0 = imu_d(1, end);
C_ib0_b = eye(3);
count = 1;
u_i0_t = zeros(3, 1);
v_i0_t = zeros(3, 1);
ts = 0.002;
ts_dmi = 0.1;
dmi_imu_greq = floor(ts_dmi / ts);
A_b = diff(dmi_d(:, 2))./ts_dmi;%A_b = c_filter_lowpass(A_b, 10);
u_i0_tl = zeros(3, 1);
u_i0_tm = zeros(3, 1);
v_i0_tl = zeros(3, 1);
v_i0_tm = zeros(3, 1);
Step = 100/ts_dmi;% 100s
Att = [];Att1 = [];Att2 = [];
e = 1 / 298.257223563;
Re = 6378160;
Cnb = eye(3);
pos0 = p0;
del_lon = 0;
K = zeros(4);A = zeros(3);
for i = 700/ts:length(imu_d)-500
% ****** init
sL = sin( P0(1) );
cL = cos( P0(1) );
tL = sL / cL;
sL2 = sL^2;
RM = Re * ( 1 - 2*e + 3*e * sL2 );
RN = Re * ( 1 + e * sL2 );
RMh = RM + P0(3);
RNh = RN + P0(3);
% ***** 初始对准****
t = imu_d(i, end) - t0;
omega_b_ib = imu_d(i, 1:3)'/ts;
f_b_sf = imu_d(i, 4:6)'/ts;
lat = pos0(1);
C_n_i0 = [-sin(omega_ie*t + del_lon), cos(omega_ie*t + del_lon), 0;
-sin(lat0)*cos(omega_ie*t + del_lon), -sin(lat0)*sin(omega_ie*t + del_lon), cos(lat);
cos(lat0)*cos(omega_ie*t + del_lon), cos(lat0)*sin(omega_ie*t + del_lon), sin(lat)];
C_e0_i0 = [cos(omega_ie*t), sin(omega_ie*t), 0;
-sin(omega_ie*t), cos(omega_ie*t), 0;
0, 0, 1];
C_n0_e0 = [0, 1, 0;
-sin(lat0), 0, cos(lat0);
cos(lat0), 0, sin(lat0)];
C_i0_n0 = (C_n0_e0 * C_e0_i0)';
C_ib0_b = C_ib0_b * (eye(3) + askew(omega_b_ib * ts));
u_i0_t = u_i0_t + C_i0_n0 * gn * ts;
% 有里程计数据
if(mod(i, dmi_imu_greq) == 0)
kdmi = i/dmi_imu_greq;
if (kdmi > length(dmi_d))
break;
end
v_b = dmi_d(kdmi, 1:3)';
a_b = [0; A_b(kdmi); 0];
omega_b_ib_mean = imu_d(i - dmi_imu_greq/2:i + dmi_imu_greq/2, 1:3)'/ts;
f_b_sf_mean = mean(imu_d(i - dmi_imu_greq/2:i + dmi_imu_greq/2, 4:6))'/ts;
v_i0_t = v_i0_t + C_ib0_b * (a_b + askew(omega_b_ib_mean) * v_b - f_b_sf_mean) * ts_dmi;
% ****update position****
vn = Cnb * v_b;
dr = vn * ts_dmi;
pos0 = pos0 + [ dr(1)/RMh; dr(3)/(RNh*cL); dr(2) ];
del_lon = pos0(2) - p0(2);
% *************wahba***********************
vib0 = v_i0_t;
vi0 = u_i0_t;
nts = ts_dmi;
dM = rq2m([0;vib0]) - lq2m([0;vi0]); % QUEST method
K = 1.0*K + dM'*dM*nts;
[v, d] = eig(K); qi0ib0 = v(:,1);
A = A + vi0*vib0'; % SVD method
% C_i0_ib0 = foam(A);% qi0ib0_SVD = m2qua(C); % FOAM method
C_i0_ib0 = q2mat(qi0ib0); % 选用严程序中的QUEST Wahba方法,看起来效果更好点
Cnb = C_n_i0 * C_i0_ib0 * C_ib0_b;
% **************
if ~isnan(m2att(C_i0_ib0))
% 保存结果
Att = [Att; m2att(Cnb)' / glv.deg, imu_d(i, end)];
Att1 = [Att1; m2att(C_i0_ib0)' / glv.deg, imu_d(i, end)];
end
count = count + 1;
end
end