基于kmines类聚线段算法

🎯 一、总体目标（Why）

把 n 条线段（用中心点 (cx, cy) 表示）分成 k 个空间上紧凑的组（簇），使得同一组内的线段彼此靠近。

这是典型的 K-Means 聚类问题 ，但只关注位置信息，忽略长度、角度等其他特征。

实际case跑出来的结果如下：

1. 高斯分布的直线类聚

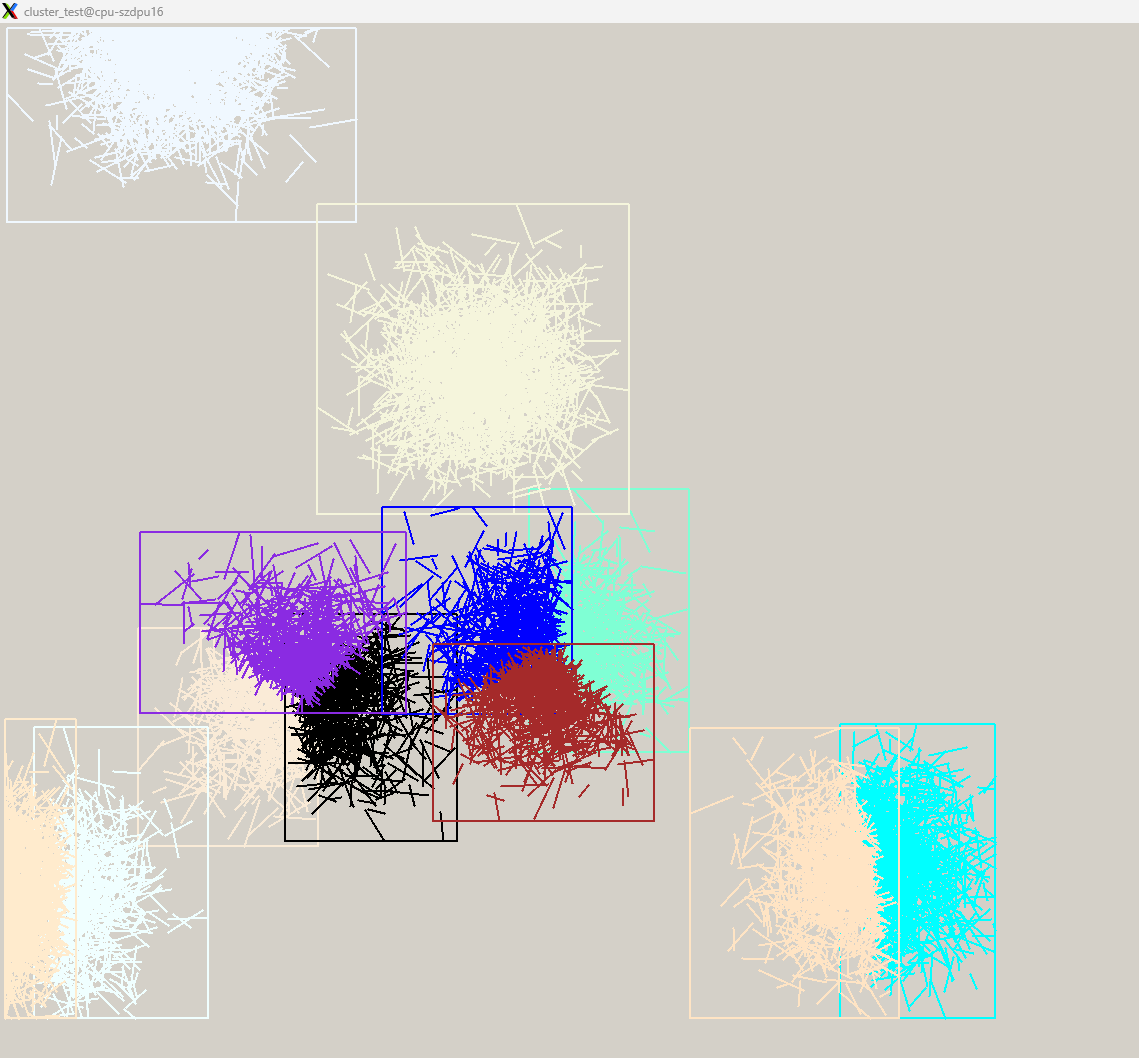
2. 均匀分布的直线类聚

---

🔧 二、函数输入输出（What）

QVector<int> kmeansPositionOnly(
    const QVector<Feature>& feature_list,  // 输入：每条线的特征（我们只用 .m_cx, .m_cy）
    int k,                                 // 想分多少个簇（box）
    int max_iters = 1000                   // 最多迭代 1000 次（防死循环）
)

返回值 ：labels[i] 表示第 i 条线属于哪个簇（取值 0 到 k-1）。

---

🧱 三、核心思想（How）------ K-Means 的两步迭代

K-Means算法思想如下：

1. 随机选取K个中心点。(KMEANS++会在选取一个中心点后更倾向于去选择离选定中心点更远的)
2. 计算其他点离哪个中心点更近，就算做哪一簇。
3. 计算每个新簇的新中心点（取平均）。
4. 重新调整除中心点外的归属情况。
5. 直到每次分簇情况相同或者中心点收敛。

K-Means 是一个迭代优化算法，每轮做两件事：

步骤	名称	做什么
1️⃣	分配（Assignment）	对每个点，找离它最近的簇中心，把它"分给"那个簇
2️⃣	更新（Update）	对每个簇，重新计算其中心（所有点的平均位置）

重复这两步，直到：

• 所有点的归属不再变化（收敛）
• 达到最大迭代次数（安全退出）

Z-score 标准化（或归一化）

1. 什么是方差（Variance）？

假设有一组数：x₁, x₂, ..., xₙ

• 先算平均值：

  μ=n1​∑i=1n​xi​

• 再算每个数离平均值有多远（偏差）：

  (xi​−μ)

• 把所有偏差平方后求平均（避免正负抵消）：

  Var(x)=n1​∑i=1n​(xi​−μ)2

👉 这个 Var(x) 就是方差。

• 方差越大 → 数据越分散
• 方差越小 → 数据越集中

2. 什么是"单位方差"？

就是让这个方差 等于 1。

怎么做到？------ 除以标准差（standard deviation）

因为：

• 标准差 = √方差 → 记作 σ
• 如果你对每个数据做变换：
  zi=σxi−μ

那么新数据 z₁, z₂, ..., zₙ 的：

• 均值 = 0
• 方差 = 1 ← 这就是"单位方差"

这个过程叫 Z-score 标准化（或归一化）。

---

📚 四、代码逐段详解

✅ 第 1 部分：边界检查 & 初始化

int n = feature_list.size();
if (n == 0 || k <= 0) return QVector<int>();  // 空输入或无效 k，直接返回
if (k > n) k = n;                             // 不能分比点还多的簇

💡 例如：只有 3 条线，却想分 10 个 box？最多只能分 3 个（每条一个簇）。

QVector<int> labels(n, 0);        // labels[i]：第 i 条线当前属于哪个簇（初始全为 0）
QVector<Feature> centroids(k);     // 存储 k 个簇的"中心点"（质心）

// 初始化质心：取前 k 个点作为初始中心
for (int i = 0; i < k; ++i)
{
    centroids[i] = feature_list[i];
}

⚠️ 这是简单初始化（不是最优的 K-Means++），但在实践中对结果影响有限，尤其当数据量大时。

---

🔁 第 2 部分：主循环 ------ 迭代优化（最多 max_iters 轮）

for (int iter = 0; iter < max_iters; ++iter)
{
    bool changed = false;  // 标记本轮是否有任何点换了簇

▶ 步骤 A：分配阶段（Assign points to nearest centroid）

for (int i = 0; i < n; ++i)
{
    int best_k = 0;
    double best_dist = dist2PositionOnly(feature_list[i], centroids[0]);

    // 遍历所有 k 个簇中心，找最近的
    for (int j = 1; j < k; ++j)
    {
        double d = dist2PositionOnly(feature_list[i], centroids[j]);
        if (d < best_dist)
        {
            best_dist = d;
            best_k = j;
        }
    }

    // 如果归属变了，记录下来
    if (labels[i] != best_k)
    {
        labels[i] = best_k;
        changed = true;
    }
}

✅ dist2PositionOnly(a, b) 只计算 (a.cx - b.cx)^2 + (a.cy - b.cy)^2，不涉及 len/ang。
🎯 目标：让每个点都"就近归队"。

▶ 提前终止：如果没人换队，说明已稳定！

if (!changed) break;  // 收敛！无需继续迭代

---

▶ 步骤 B：更新阶段（Recompute centroids）

QVector<Feature> new_centroids(k);  // 临时累加和
QVector<int> counts(k, 0);          // 每个簇有多少个点

// 遍历所有点，按当前标签累加到对应簇
for (int i = 0; i < n; ++i)
{
    int cid = labels[i];  // 当前点属于哪个簇
    new_centroids[cid].m_cx += feature_list[i].m_cx;
    new_centroids[cid].m_cy += feature_list[i].m_cy;
    counts[cid]++;
}

// 正式更新质心 = 平均位置
for (int i = 0; i < k; ++i)
{
    if (counts[i] > 0)
    {
        centroids[i].m_cx = new_centroids[i].m_cx / counts[i];
        centroids[i].m_cy = new_centroids[i].m_cy / counts[i];
        // 注意：len/ang 不参与聚类，所以不更新（保持原值也无影响）
    }
    else
    {
        // ❗ 处理"空簇"：某个簇没被分配任何点
        centroids[i] = feature_list[qrand() % n];  // 随机选一个点作为新中心
    }
}

💡 "空簇"问题 ：当 k 设得太大，或初始中心太集中，某些簇可能没人"认领"。

解决方案：随机重置，避免该簇永远为空导致算法失效。

---

📤 第 3 部分：返回结果

return labels;  // 每个点的最终簇编号

这个 labels 向量会被用于：

• 分组线段
• 计算每个组的包围盒（Box）
• 输出最终的聚类结果

---

🌟 五、关键设计亮点（针对你的需求）

特性	说明
仅用位置 (cx, cy)	忽略长度、角度，确保空间邻近的线被分在一起
标准化已在调用前完成	所以这里直接使用归一化后的坐标，保证 x/y 尺度一致
处理空簇	随机重置，提升鲁棒性
提前收敛	一旦稳定就退出，节省计算
最大迭代保护	max_iters=1000 防止极端情况卡死（实际通常 10~50 轮就收敛）

---

📊 六、举个小例子（k=2）

假设 4 条线的中心点（已标准化）：

• L0: (-1.0, -0.9)
• L1: (-0.8, -1.1)
• L2: (0.9, 1.0)
• L3: (1.1, 0.8)

1. 初始质心：C0 = L0, C1 = L1
2. 第1轮分配 ：
   • L0, L1 → C0
   • L2, L3 → C1（因为离 C1 更近？其实要看距离）
3. 更新质心 ：
   • C0 = avg(L0,L1) ≈ (-0.9, -1.0)
   • C1 = avg(L2,L3) ≈ (1.0, 0.9)
4. 第2轮分配 ：结果不变 → 收敛！
5. 返回 labels = [0, 0, 1, 1]

✅ 成功分成左右两组！

---

✅ 七、总结：这段代码的实现思路

1. 目标明确 ：按空间位置将线段聚成 k 组。
2. 算法选择：使用经典 K-Means（分配 + 更新迭代）。
3. 特征简化 ：只用 (cx, cy)，忽略干扰项。
4. 健壮性保障 ：
   • 边界检查
   • 空簇处理
   • 提前收敛
   • 最大迭代限制
5. 工程友好：接口简单，结果可直接用于后续 Box 构建。

---

你现在完全掌握了这段代码的设计哲学与实现细节 ！

它是一个轻量、高效、可靠的 K-Means 实现，专为你"可控数量 box"的需求量身定制 ✅

如需进一步优化（如 K-Means++ 初始化、多线程加速、支持权重等），也可以在此基础上扩展。

整体代码如下：

struct Feature
{
    double m_cx, m_cy, m_len, m_ang;
    Feature(double cx = 0.0, double cy = 0.0, double len = 0.0, double ang = 0.0)
        : m_cx(cx),
          m_cy(cy),
          m_len(len),
          m_ang(ang)
    {
    }
};

static inline double dist2PositionOnly(const Feature& a, const Feature& b)
{
    double dx = a.m_cx - b.m_cx;
    double dy = a.m_cy - b.m_cy;
    return dx * dx + dy * dy;
}

static void standardizePositionOnly(QVector<Feature>& feature_list)
{
    int n = feature_list.size();
    if (n == 0)
        return;

    double mean_cx = 0.0, mean_cy = 0.0;
    for (int i = 0; i < n; ++i)
    {
        mean_cx += feature_list[i].m_cx;
        mean_cy += feature_list[i].m_cy;
    }
    mean_cx /= n;
    mean_cy /= n;

    double var_cx = 0.0, var_cy = 0.0;
    for (int i = 0; i < n; ++i)
    {
        double dx = feature_list[i].m_cx - mean_cx;
        double dy = feature_list[i].m_cy - mean_cy;
        var_cx += dx * dx;
        var_cy += dy * dy;
    }
    var_cx /= n;
    var_cy /= n;

    double std_cx = qSqrt(var_cx);
    double std_cy = qSqrt(var_cy);
    if (std_cx < 1e-12)
        std_cx = 1.0;
    if (std_cy < 1e-12)
        std_cy = 1.0;

    for (int i = 0; i < n; ++i)
    {
        feature_list[i].m_cx = (feature_list[i].m_cx - mean_cx) / std_cx;
        feature_list[i].m_cy = (feature_list[i].m_cy - mean_cy) / std_cy;
    }
}

static QVector<int> kmeansPositionOnly(const QVector<Feature>& feature_list, int k, int max_iters)
{
    int n = feature_list.size();
    if (n == 0 || k <= 0)
        return QVector<int>();

    if (k > n)
        k = n;

    QVector<int> labels(n, 0);
    QVector<Feature> centroids(k);

    qsrand(QTime::currentTime().msec());
    for (int i = 0; i < k; ++i)
    {
        centroids[i] = feature_list[qrand() % n];
    }

    for (int iter = 0; iter < max_iters; ++iter)
    {
        bool changed = false;

        for (int i = 0; i < n; ++i)
        {
            int best_k = 0;
            double best_dist = dist2PositionOnly(feature_list[i], centroids[0]);
            for (int j = 1; j < k; ++j)
            {
                double d = dist2PositionOnly(feature_list[i], centroids[j]);
                if (d < best_dist)
                {
                    best_dist = d;
                    best_k = j;
                }
            }
            if (labels[i] != best_k)
            {
                labels[i] = best_k;
                changed = true;
            }
        }

        if (!changed)
            break;

        QVector<Feature> new_centroids(k);
        QVector<int> counts(k, 0);

        for (int i = 0; i < n; ++i)
        {
            int cid = labels[i];
            new_centroids[cid].m_cx += feature_list[i].m_cx;
            new_centroids[cid].m_cy += feature_list[i].m_cy;
            counts[cid]++;
        }

        for (int i = 0; i < k; ++i)
        {
            if (counts[i] > 0)
            {
                centroids[i].m_cx = new_centroids[i].m_cx / counts[i];
                centroids[i].m_cy = new_centroids[i].m_cy / counts[i];
            }
            else
            {
                centroids[i] = feature_list[qrand() % n];
            }
        }
    }

    return labels;
}

static Box computeBoundingBox(const QVector<Line>& lines)
{
    if (lines.isEmpty())
        return Box(0, 0, 0, 0);

    double xmin = std::numeric_limits<double>::max();
    double ymin = std::numeric_limits<double>::max();
    double xmax = -std::numeric_limits<double>::max();
    double ymax = -std::numeric_limits<double>::max();

    for (const Line& line : lines)
    {
        xmin = qMin(xmin, qMin(line.p1().x(), line.p2().x()));
        ymin = qMin(ymin, qMin(line.p1().y(), line.p2().y()));
        xmax = qMax(xmax, qMax(line.p1().x(), line.p2().x()));
        ymax = qMax(ymax, qMax(line.p1().y(), line.p2().y()));
    }

    return Box(xmin, ymin, xmax, ymax);
}

QVector<ClusterResult> Algorithm::clusterLines(const QVector<Line>& lines, int k, int max_iters)
{
    QVector<ClusterResult> results;
    if (lines.isEmpty() || k <= 0)
        return results;

    QVector<Feature> features;
    features.reserve(lines.size());
    for (int i = 0; i < lines.size(); ++i)
    {
        const Line& line = lines[i];
        double cx = (line.p1().x() + line.p2().x()) * 0.5;
        double cy = (line.p1().y() + line.p2().y()) * 0.5;
        features.append(Feature(cx, cy, 0.0, 0.0));
    }
    standardizePositionOnly(features);

    QVector<int> labels = kmeansPositionOnly(features, k, max_iters);

    QVector<QVector<Line>> groups(k);
    for (int i = 0; i < lines.size(); ++i)
    {
        int cid = labels[i];
        if (cid < 0 || cid >= k)
            cid = 0;
        groups[cid].append(lines[i]);
    }

    for (int i = 0; i < k; ++i)
    {
        if (groups[i].isEmpty())
            continue;
        Box box = computeBoundingBox(groups[i]);
        results.append(ClusterResult(box, groups[i]));
    }


    return results;
}