数据结构第四章：串

一、什么是"串"？

在数据结构中，串（String）是由零个或多个字符组成的有限序列 。

比如 "hello"、"a+b*c" 都是串。

• 主串：被查找的长字符串（如文本）
• 子串：主串中任意连续的一段（如关键词）
• 空串：长度为 0 的串（不是空格！）

✅ 小考点 ：空格 ' ' 是一个有效字符，计入串长！

---

二、串的存储结构（选择题常考）

表格

存储方式	特点	优缺点
定长顺序存储	用固定长度数组存储	简单，但空间浪费或溢出
堆分配存储	动态申请内存（C 语言 malloc）	长度可变，最常用
块链存储	每块存若干字符，用链表连接	适合超长串，但指针开销大

📌 考研重点：堆分配是实际应用中最灵活的方式；定长适合已知长度的场景。

🔹 定长顺序存储结构：

#define MaxLen 255 //预定义最大串长为255
typedef struct { 
    char ch[MaxLen]; //每个分量存储一个字符
    int length; //串的实际长度
} SString;

🔹 堆分配存储结构：

typedef struct {
    char *ch; //按串长分配存储区，ch 指向串的基地址
    int length; //串的长度
} HString;

🔹 块链存储结构：

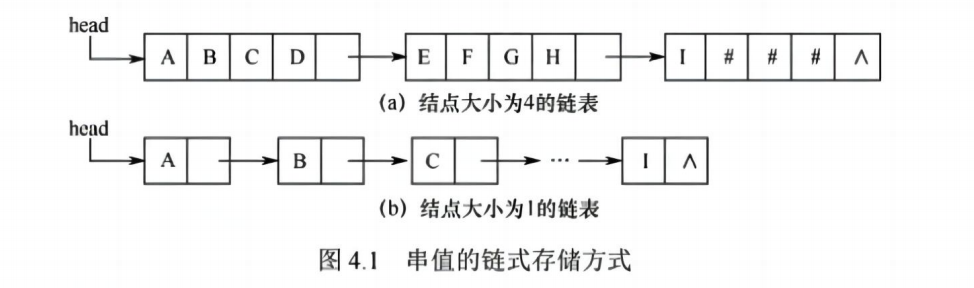
最后一个结点占不满时通常用"#"补上

三、模式匹配：暴力法 vs KMP（重中之重！）

1. 暴力匹配法（Brute Force）

#define MaxLen 255 //预定义最大串长为255
typedef struct { 
    char ch[MaxLen]; //每个分量存储一个字符
    int length; //串的实际长度
} SString;

// 简单的模式匹配算法 S: 主串 T: 子串 返回：字串在主串中的首字符位置下标
int index(SString S, SString T) {
    // 字符串S下标
    int i = 1;
    // 查找的子串T
    int j = 1;
    while(i <= S.length && j <= T.length) {
        if(S.ch[i] == T.ch[j]) { //当前字符匹配
            //继续比较后继字符
            i++;
            j++;
        } else { // 当前字符不匹配
            //指针后退重新开始匹配
            i = i - j + 2;
            j = 1;
        }
    }
    if(j > T.length) {
        return i - T.length;
    } else {
        return 0;
    }
}

2. KMP 算法：不回退的高效匹配

KMP 的核心思想就一句：

"利用已经匹配的信息，让模式串尽可能多地'滑动'，避免主串指针回退。"

🔑 关键：next 数组

next[i] 表示：模式串前 i 个字符中，最长相等真前后缀的长度。

• 真前后缀：不能是整个串本身，也不能是空串。
• 作用 ：当第 i 位失配时，模式串跳到 next[i] 位置继续匹配。

✅ 手动构造 next 数组（以 "ababaa" 为例）

表格

i（从1开始）	1	2	3	4	5	6
字符	a	b	a	b	a	a
next[i]	0	0	1	2	3	1

构造逻辑简述：

• i=1：单个字符，无真前后缀 → 0
• i=3："aba"，前缀 "a" = 后缀 "a" → 长度 1
• i=6："ababaa"，最长相等真前后缀是 "a" → 长度 1

📌 考研必考：给一个模式串，手算 next 数组！

3. KMP 匹配过程（主串指针永不回退！）

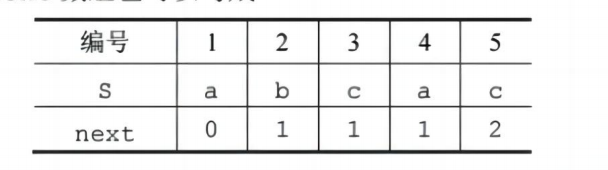
这里使用新的next[]数组,基于标准的next数组做了变更

1.标准next数组：

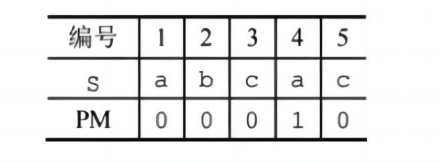
2. PM表向右移移动一位

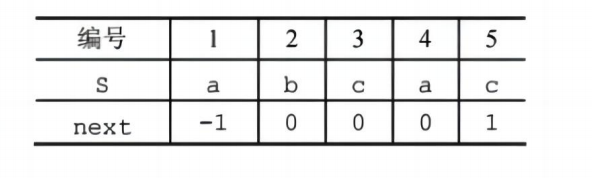
3. next数组整体+1

#define MaxLen 255 //预定义最大串长为255
typedef struct { 
    char ch[MaxLen]; //每个分量存储一个字符
    int length; //串的实际长度
} SString; 

// KMP匹配 S: 主串 T: 子串 next[]: PM表
int index_KMP(SString S, SString T, int next[]) {
    // 主串S的下标
    int i = 1;
    // 子串T的下标
    int j = 1;
    while(i <= S.length && j <= T.length) {
        if(j == 0 || S.ch[i] == T.ch[j]) { // 当前字符匹配 或 子串第一个元素匹配失败
            // 继续比较后继字符
            i++;
            j++;
        } else { // 当前字符不匹配
            j = next[j];
        }
    }
    if(j > T.length) {
        return i - T.length;
    } else {
        return 0;
    }
}

时间复杂度： O(m+n)O(m+n) ------ 线性时间，完胜暴力法！

4. KMP算法的进一步优化

• 若 T.ch[j] == T.ch[next[j]]，则 nextval[j] = nextval[next[j]]
• 否则，nextval[j] = next[j]

📌 注意：使用 nextval[next[j]]（而非 next[next[j]]）是为了递归跳过所有相同字符 ，确保最终指向一个不同字符的位置。