探索基于FPGA的自适应滤波器实现之旅：2023年H题实战

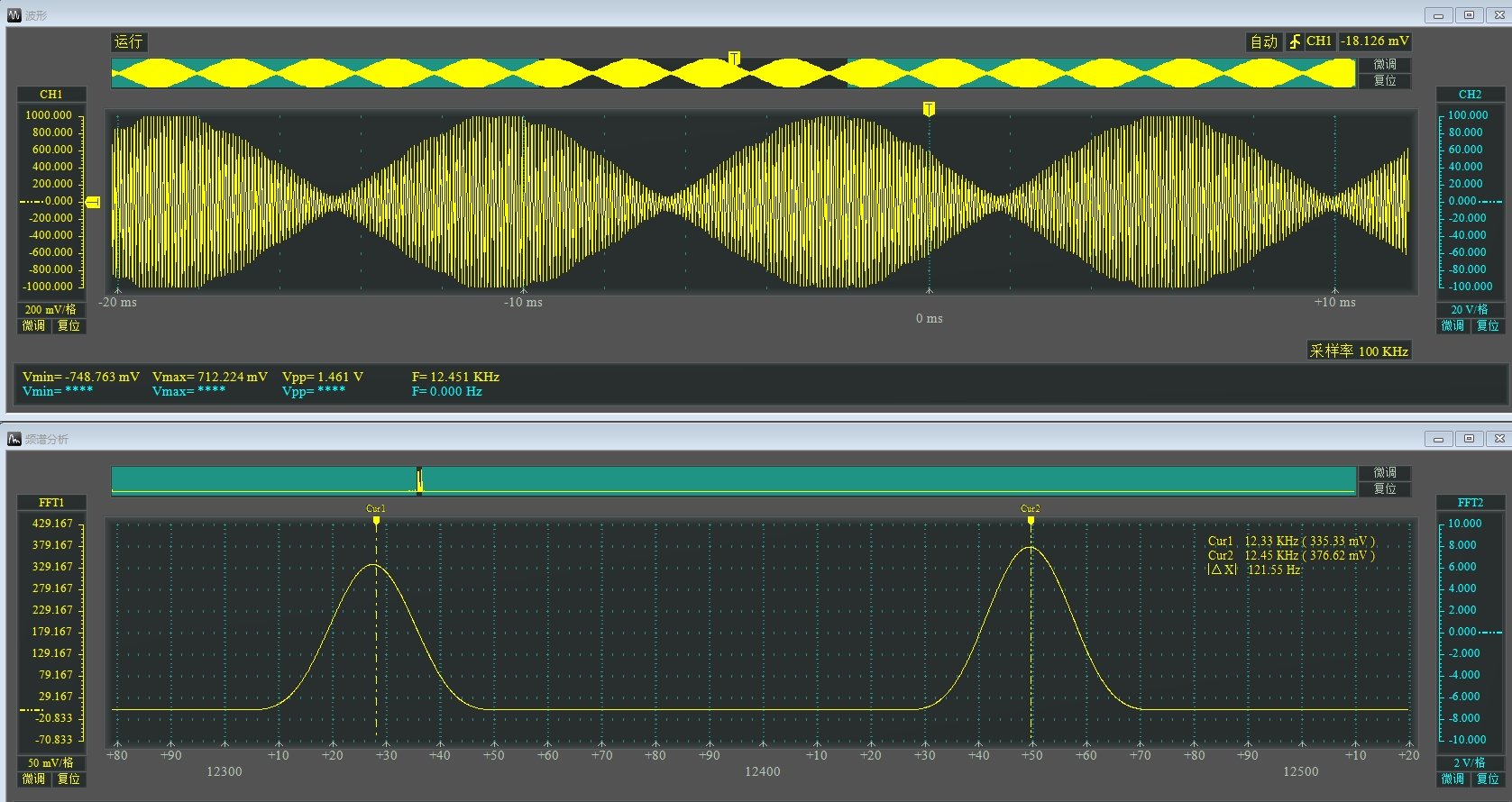
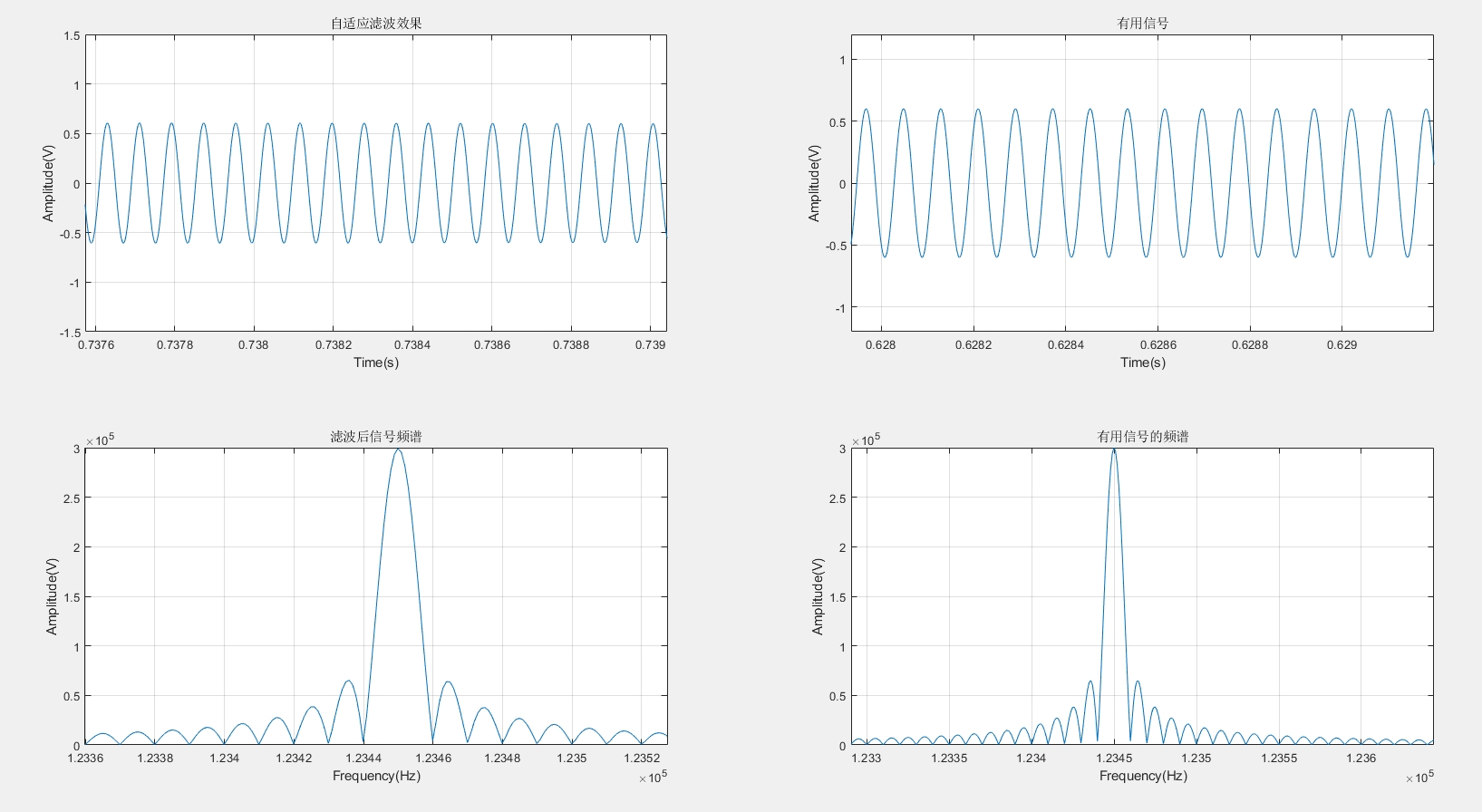
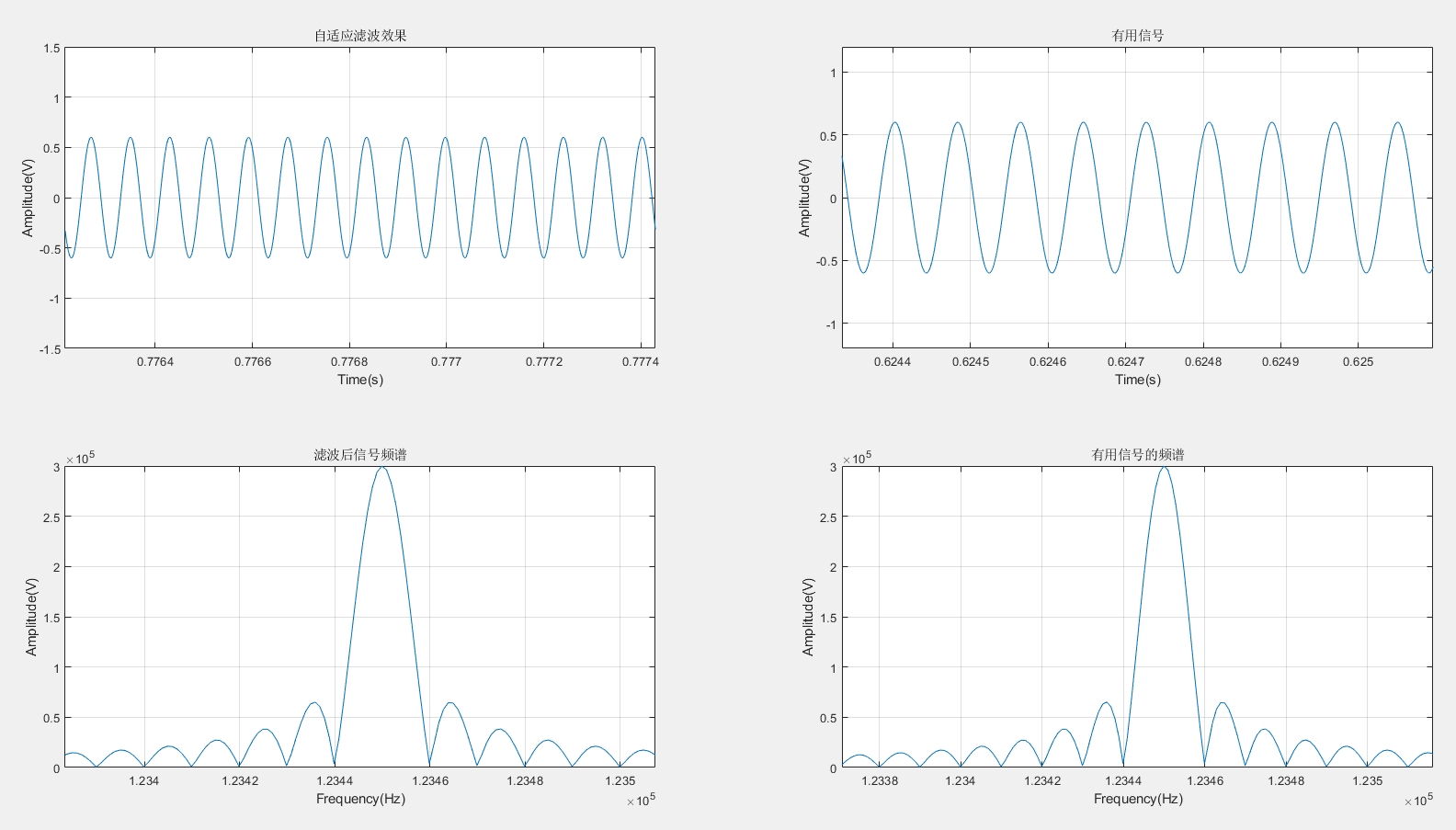
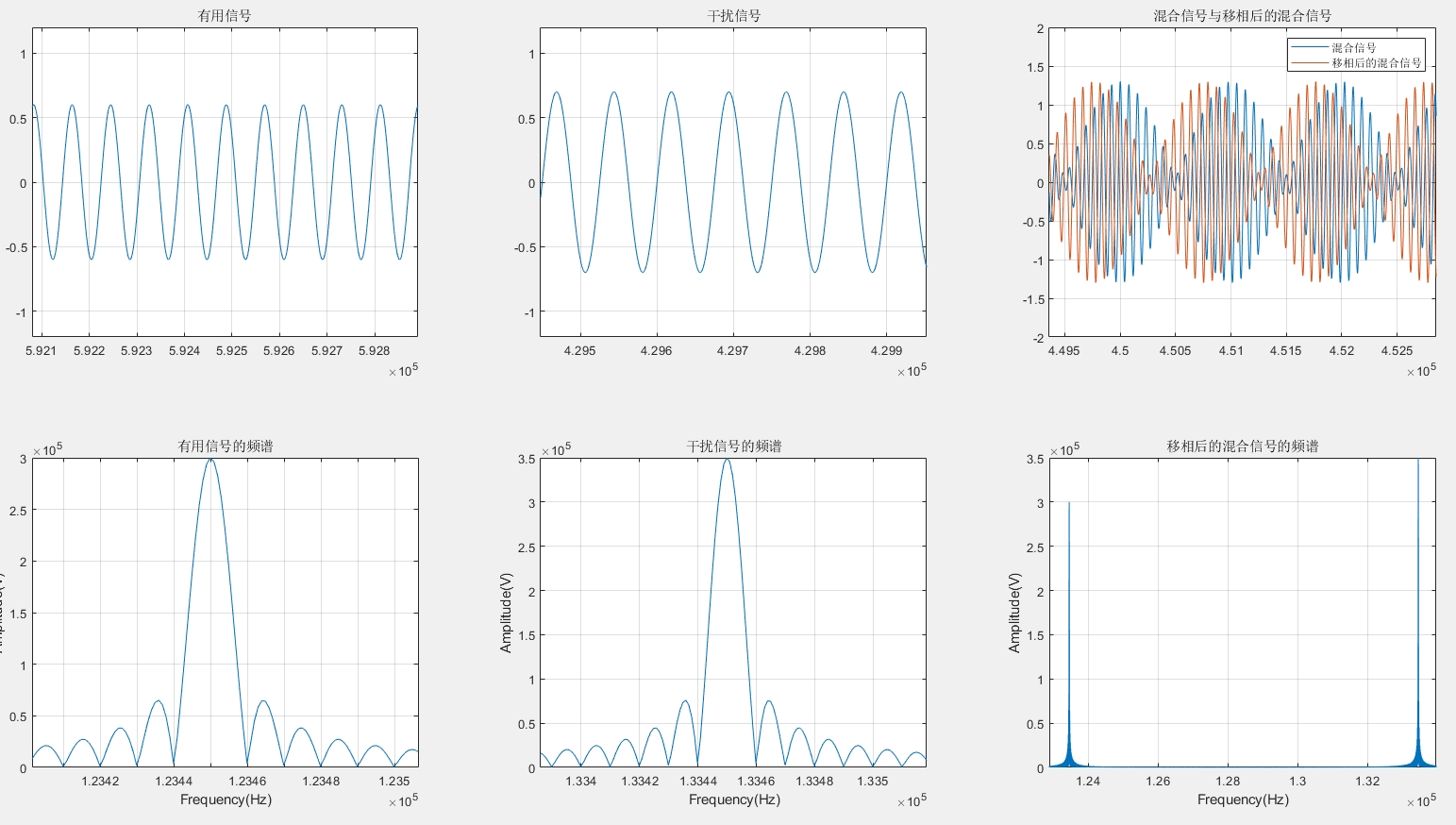
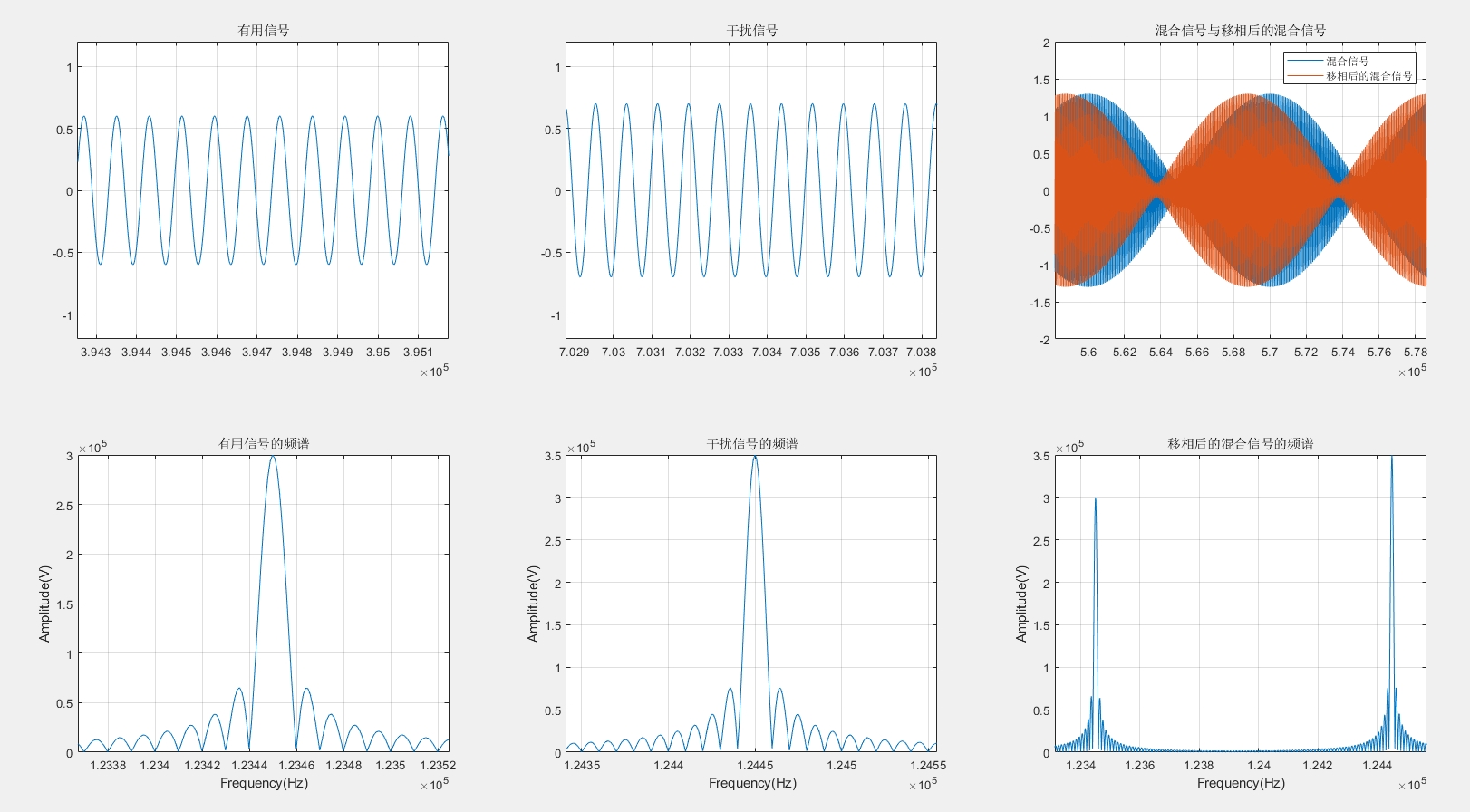
基于FPGA的自适应滤波器FIR/IIR滤波器LMS/NLMS/RLS算法/FxLMS/分数阶 2023年H题本设计是在FPGA开发板上实现一个自适应滤波器，只需要输入于扰信号和期望信号(混合信号)即可得到滤波输出，使用非常简单。

在数字信号处理领域，自适应滤波器是一项非常重要的技术。而2023年H题聚焦于在FPGA开发板上实现自适应滤波器，着实是个有趣且具挑战性的任务。

滤波器类型：FIR与IIR

FIR（有限冲激响应）滤波器和IIR（无限冲激响应）滤波器是两种最常见的滤波器类型。

FIR滤波器

FIR滤波器的输出仅取决于当前和过去的输入值，不存在反馈回路，这使得它在稳定性方面具有先天优势。其冲激响应在有限时间内衰减为零。

例如，一个简单的3阶FIR滤波器的差分方程可以表示为：

verilog 复制代码

// 假设输入信号为x，输出信号为y
// 定义延迟寄存器
reg [15:0] x_delay1, x_delay2; 
always @(posedge clk or posedge rst) begin
    if (rst) begin
        y <= 16'd0;
        x_delay1 <= 16'd0;
        x_delay2 <= 16'd0;
    end else begin
        x_delay2 <= x_delay1;
        x_delay1 <= x;
        y <= coef0 * x + coef1 * x_delay1 + coef2 * x_delay2;
    end
end

这里通过寄存器来延迟输入信号 x，然后与相应的系数 coef0、coef1、coef2 相乘并累加得到输出 y。这种结构简单直观，易于在FPGA上实现。

IIR滤波器

与FIR不同，IIR滤波器存在反馈回路，其输出不仅依赖于当前和过去的输入，还与过去的输出有关。这使得IIR滤波器能够用较低的阶数实现较为复杂的滤波特性。但由于反馈回路的存在，稳定性需要特别关注。

以一个简单的一阶IIR低通滤波器为例，其差分方程为：

verilog 复制代码

reg [15:0] y_delay; 
always @(posedge clk or posedge rst) begin
    if (rst) begin
        y <= 16'd0;
        y_delay <= 16'd0;
    end else begin
        y <= a0 * x + a1 * x_delay + b1 * y_delay;
        y_delay <= y;
    end
end

这里除了考虑当前和延迟的输入信号 x 与系数相乘，还考虑了上一时刻的输出 y_delay 与系数 b1 相乘，体现了反馈的特性。

自适应算法

LMS算法

最小均方（LMS）算法是自适应滤波器中最常用的算法之一。它的核心思想是通过不断调整滤波器的系数，使得滤波器输出与期望信号之间的误差平方和最小。

verilog 复制代码

// LMS算法更新系数示例
always @(posedge clk or posedge rst) begin
    if (rst) begin
        for (int i = 0; i < num_taps; i = i + 1) begin
            coef[i] <= initial_coef[i];
        end
    end else begin
        error = desired_signal - y;
        for (int i = 0; i < num_taps; i = i + 1) begin
            coef[i] <= coef[i] + 2 * mu * error * x_delay[i];
        end
    end
end

这里 mu 是步长因子，它控制着系数更新的速度。步长太大可能导致系统不稳定，步长太小则收敛速度慢。每次迭代时，根据当前的误差 error 来调整滤波器的系数 coef。

NLMS算法

归一化最小均方（NLMS）算法是对LMS算法的改进。在LMS算法中，步长固定，而NLMS算法根据输入信号的能量来动态调整步长，使得收敛速度更快且稳定性更好。

verilog 复制代码

always @(posedge clk or posedge rst) begin
    if (rst) begin
        for (int i = 0; i < num_taps; i = i + 1) begin
            coef[i] <= initial_coef[i];
        end
    end else begin
        error = desired_signal - y;
        power = 0;
        for (int i = 0; i < num_taps; i = i + 1) begin
            power = power + x_delay[i] * x_delay[i];
        end
        if (power > 0) begin
            for (int i = 0; i < num_taps; i = i + 1) begin
                coef[i] <= coef[i] + 2 * mu / (delta + power) * error * x_delay[i];
            end
        end
    end
end

这里通过计算输入信号延迟值的功率 power，并结合一个小的常数 delta 来归一化步长，从而优化了系数更新过程。

RLS算法

递归最小二乘（RLS）算法从另一个角度来调整滤波器系数，它试图最小化加权的误差平方和。与LMS和NLMS相比，RLS算法收敛速度更快，但计算复杂度较高。

verilog 复制代码

// RLS算法简化实现框架
always @(posedge clk or posedge rst) begin
    if (rst) begin
        P = eye_matrix; // 初始化P矩阵为单位矩阵
        for (int i = 0; i < num_taps; i = i + 1) begin
            coef[i] <= initial_coef[i];
        end
    end else begin
        phi = {x_delay[num_taps - 1],..., x_delay[0]}; // 构造数据向量
        K = P * phi / (lambda + phi' * P * phi);
        error = desired_signal - y;
        for (int i = 0; i < num_taps; i = i + 1) begin
            coef[i] <= coef[i] + K[i] * error;
        end
        P = (eye_matrix - K * phi') * P / lambda;
    end
end

这里 lambda 是遗忘因子，控制着旧数据对系数更新的影响程度。P 矩阵的更新和系数 coef 的更新都相对复杂，涉及矩阵运算，但带来了更快的收敛效果。

FxLMS算法

FxLMS（Filtered - x Least Mean Square）算法主要用于有源噪声控制等领域。它在LMS算法的基础上，对输入信号进行预滤波处理。

verilog 复制代码

// FxLMS算法示例
always @(posedge clk or posedge rst) begin
    if (rst) begin
        for (int i = 0; i < num_taps; i = i + 1) begin
            coef[i] <= initial_coef[i];
        end
    end else begin
        xf = filter(x); // 对输入信号x进行预滤波得到xf
        y = dot_product(coef, xf_delay);
        error = desired_signal - y;
        for (int i = 0; i < num_taps; i = i + 1) begin
            coef[i] <= coef[i] + 2 * mu * error * xf_delay[i];
        end
    end
end

先通过一个滤波器对输入信号 x 进行处理得到 xf，后续的系数更新基于 xf 的延迟值和误差来进行，从而更好地适应特定的噪声控制场景。

分数阶自适应滤波器

分数阶自适应滤波器在传统整数阶滤波器的基础上引入分数阶微积分的概念。它能够提供更灵活的滤波特性，在某些特殊应用场景下表现出色。其实现相对复杂，涉及到分数阶微积分的数字近似。

verilog 复制代码

// 分数阶滤波器系数更新简单示意
always @(posedge clk or posedge rst) begin
    if (rst) begin
        for (int i = 0; i < num_taps; i = i + 1) begin
            coef[i] <= initial_coef[i];
        end
    end else begin
        frac_delay_x = fractional_delay(x); // 对输入进行分数阶延迟
        y = dot_product(coef, frac_delay_x_delay);
        error = desired_signal - y;
        for (int i = 0; i < num_taps; i = i + 1) begin
            coef[i] <= coef[i] + 2 * mu * error * frac_delay_x_delay[i];
        end
    end
end

这里通过对输入信号进行分数阶延迟操作，然后基于延迟后的信号进行系数更新，以实现独特的滤波性能。

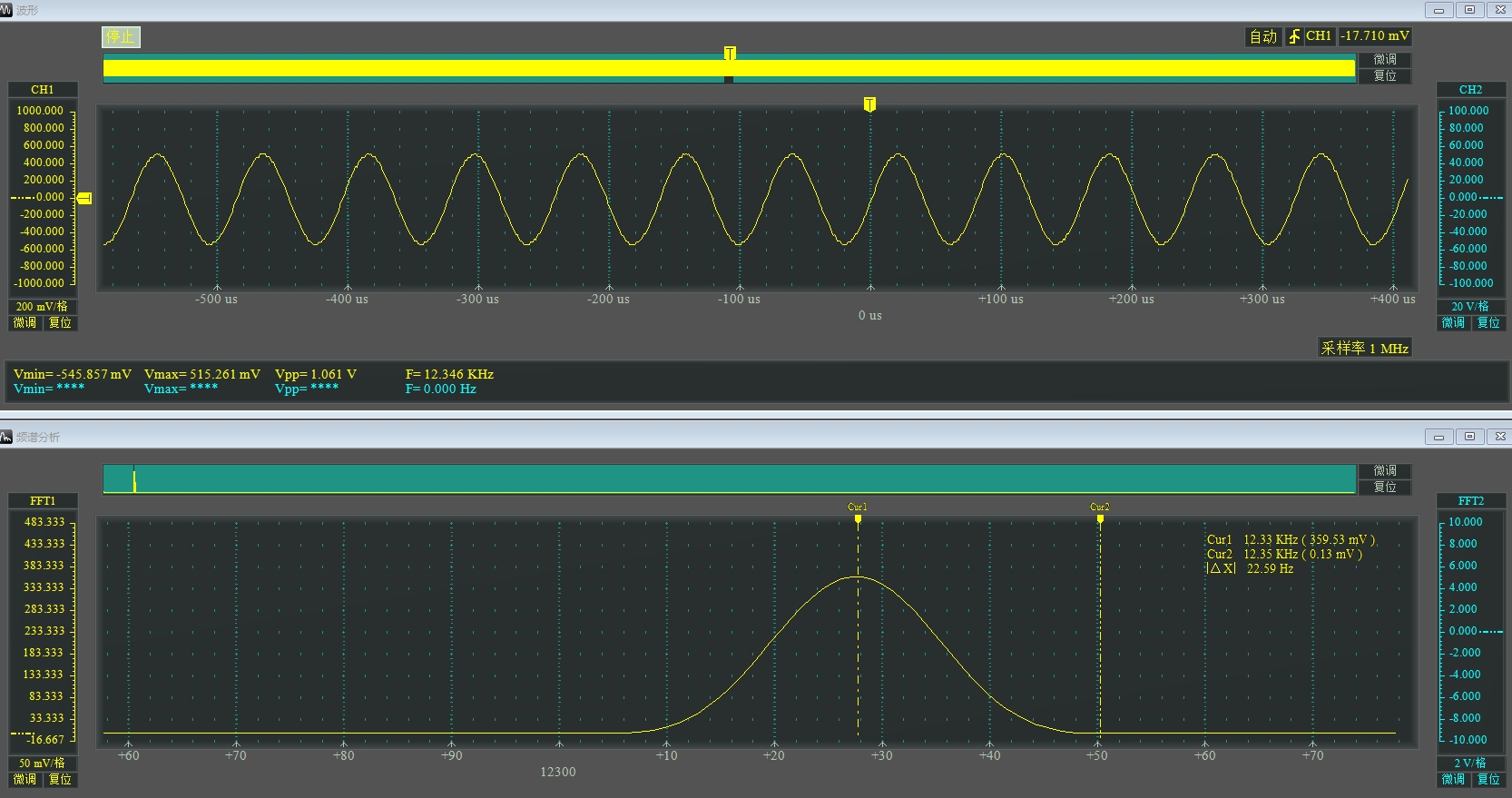
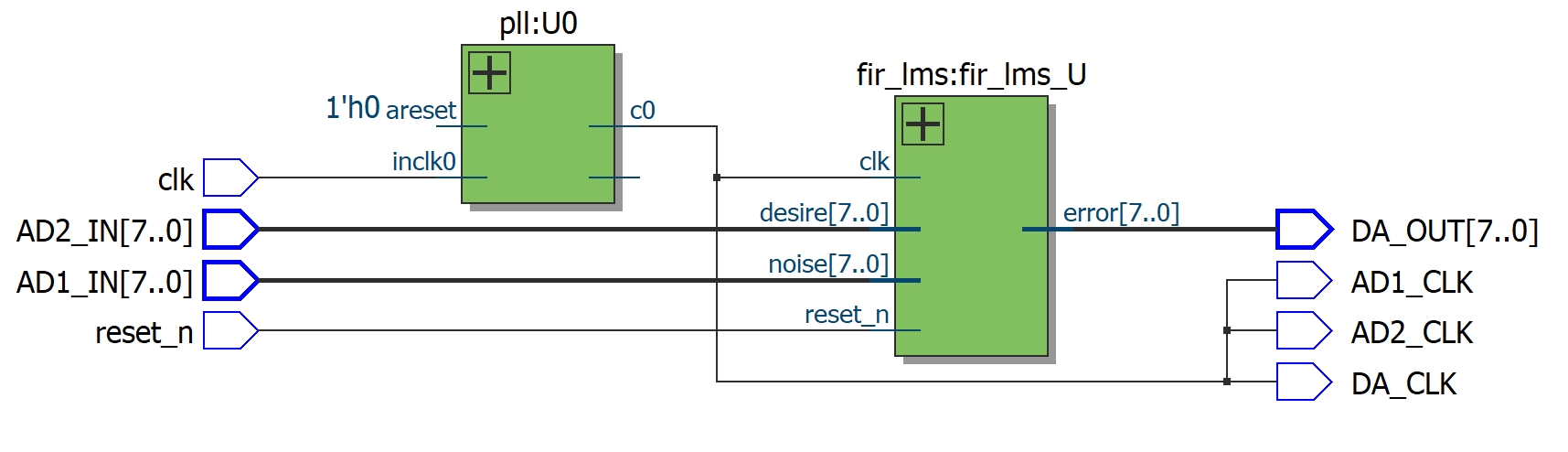
本设计基于FPGA开发板，通过简单地输入干扰信号和期望信号（混合信号），就能得到滤波输出，为实际应用提供了便利。在实现过程中，我们可以根据具体需求，如实时性、资源占用、滤波性能等，选择合适的滤波器类型（FIR或IIR）以及自适应算法，在FPGA这片神奇的"数字画布"上绘制出满足需求的自适应滤波器蓝图。