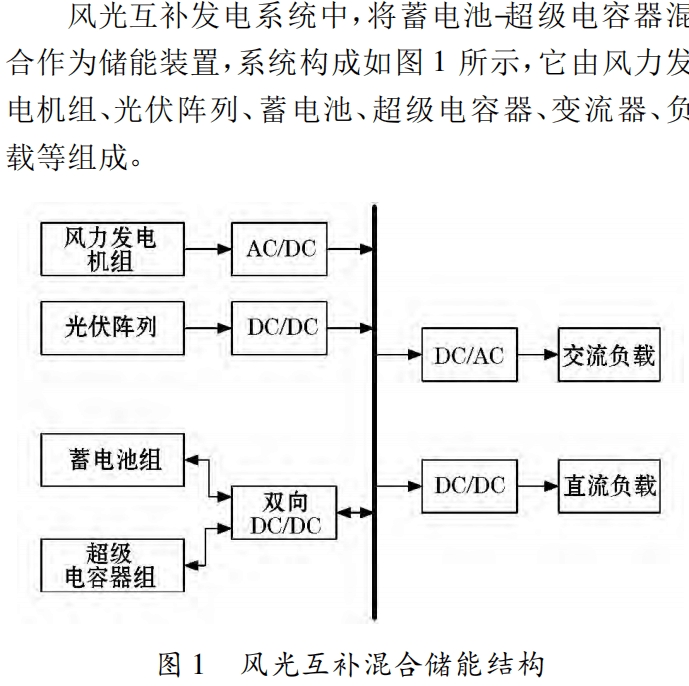
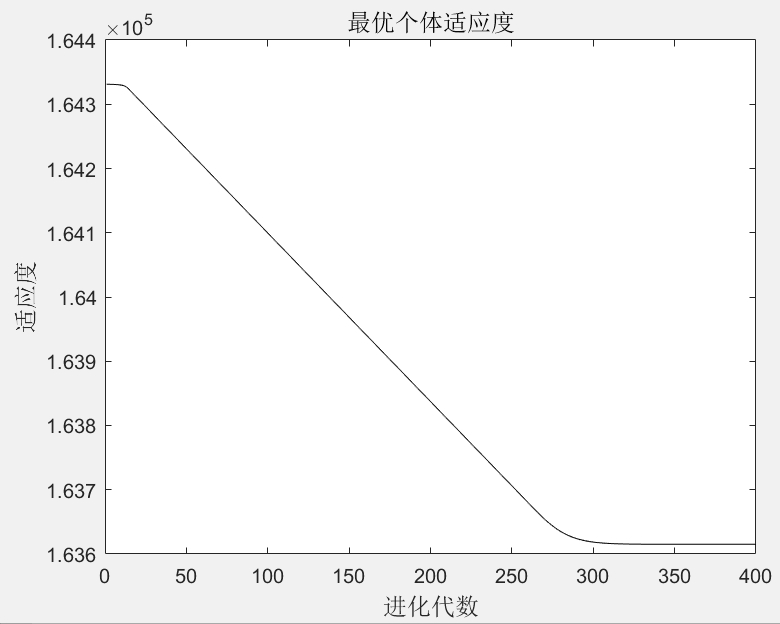
混合储能系统容量优化：基于粒子群算法的Matlab实现

混合储能系统容量优化matlab 采用粒子群算法编制风光互补发电储能系统的容量优化程序，程序采用超级电容和蓄电池的方案，得到最佳蓄电池和超级电容个数。

在可再生能源蓬勃发展的今天，风光互补发电储能系统因其能有效整合风能与太阳能资源，成为了众多研究与应用的热点。而混合储能系统，特别是采用超级电容和蓄电池组合的方案，更是为系统稳定运行和高效能量管理提供了有力保障。今天，咱就聊聊如何用粒子群算法在Matlab里实现这个混合储能系统的容量优化，算出最佳的蓄电池和超级电容个数。

粒子群算法基础

粒子群算法（PSO），简单来说，它模拟鸟群觅食行为。想象一群鸟在空间里找食物，每只鸟就是一个"粒子"，它们在搜索空间中根据自己的经验（历史最优位置）和同伴的经验（全局最优位置）来调整自己的飞行方向和速度。每个粒子都有自己的位置和速度，位置就对应着我们要求解的问题的可能解，像这里就是蓄电池和超级电容的个数组合。

Matlab实现代码框架

初始化部分

matlab 复制代码

% 粒子群算法参数设置
num_particles = 50; % 粒子数量
num_dimensions = 2; % 维度，这里是蓄电池和超级电容个数，所以是2
max_iterations = 100; % 最大迭代次数
c1 = 1.5; % 学习因子1
c2 = 1.5; % 学习因子2
w_max = 0.9; % 惯性权重最大值
w_min = 0.4; % 惯性权重最小值

% 初始化粒子位置和速度
particles_positions = rand(num_particles, num_dimensions); % 在0 - 1之间随机初始化位置
particles_velocities = rand(num_particles, num_dimensions); % 在0 - 1之间随机初始化速度

% 初始化个体最优位置和全局最优位置
personal_best_positions = particles_positions;
personal_best_fitness = Inf(num_particles, 1);
global_best_position = [];
global_best_fitness = Inf;

这部分代码设置了粒子群算法的基础参数，比如粒子数量、维度（对应蓄电池和超级电容两个变量）、最大迭代次数等。然后随机初始化粒子的位置和速度，并且为每个粒子设置初始的个体最优位置，同时初始化全局最优位置和适应度值。

适应度函数定义

适应度函数就是衡量每个粒子位置好坏的标准，在我们这个风光互补发电储能系统容量优化里，它应该和系统成本、稳定性等因素相关。假设我们简单定义一个以系统成本最小为目标的适应度函数，比如系统成本 = 蓄电池成本 蓄电池个数 + 超级电容成本 超级电容个数。

matlab 复制代码

function fitness = cost_function(position)
    battery_cost = 100; % 假设每个蓄电池成本100元
    supercapacitor_cost = 50; % 假设每个超级电容成本50元
    fitness = battery_cost * position(1) + supercapacitor_cost * position(2);
end

这里的代码很直观，接受一个粒子的位置（也就是蓄电池和超级电容个数的组合），根据假设的成本计算出这个组合对应的系统成本作为适应度值。

迭代更新部分

matlab 复制代码

for iteration = 1:max_iterations
    w = w_max - (w_max - w_min) * iteration / max_iterations; % 线性递减惯性权重

    for i = 1:num_particles
        % 计算适应度
        fitness = cost_function(particles_positions(i, :));

        % 更新个体最优
        if fitness < personal_best_fitness(i)
            personal_best_fitness(i) = fitness;
            personal_best_positions(i, :) = particles_positions(i, :);
        end

        % 更新全局最优
        if fitness < global_best_fitness
            global_best_fitness = fitness;
            global_best_position = particles_positions(i, :);
        end

        % 更新速度和位置
        r1 = rand(1, num_dimensions);
        r2 = rand(1, num_dimensions);
        particles_velocities(i, :) = w * particles_velocities(i, :) + c1 * r1.* (personal_best_positions(i, :) - particles_positions(i, :)) + c2 * r2.* (global_best_position - particles_positions(i, :));
        particles_positions(i, :) = particles_positions(i, :) + particles_velocities(i, :);

        % 边界处理，确保粒子位置在合理范围内，比如蓄电池和超级电容个数不能为负
        particles_positions(i, particles_positions(i, :) < 0) = 0;
    end
end

在每次迭代中，首先计算线性递减的惯性权重。然后对每个粒子计算适应度，根据适应度更新个体最优和全局最优。接着按照粒子群算法的公式更新粒子的速度和位置。最后进行边界处理，保证蓄电池和超级电容个数是非负的。

总结

通过以上Matlab代码实现，利用粒子群算法就可以在一定假设条件下找到风光互补发电储能系统中，采用超级电容和蓄电池组合方案时的最佳蓄电池和超级电容个数，实现混合储能系统容量的优化。当然，实际应用中，适应度函数可以根据更多复杂的因素，比如系统效率、寿命等进行更精确的定义，进一步提升优化效果。希望这篇博文能给对混合储能系统容量优化感兴趣的小伙伴一些启发。