FPGA教程系列-流水线思想初识

流水线设计是一种典型的面积换性能的设计。一方面通过对长功能路径的合理划分，在同一时间内同时并行多个该功能请求，大大提高了某个功能的吞吐率；另一方面由于长功能路径被切割成短路径，可以达到更高的工作频率，如果不需要提高工作频率，多出来的提频空间可以用于降压降功耗。流水线设计是完美的时间并行。因为流水线上每一级的处理都是一个时钟周期的延时，并且一动则全动，每一级的延时可以完美的掩盖起来，最高实现与流水级数相同数量的请求并行度。

简单来说，流水线思想就是：将一个耗时长的复杂任务，切分成若干个耗时短的小任务，并让它们重叠执行。

先列一个简单的例子，一个加法器如下：

verilog 复制代码

`timescale 1ns / 1ps
//
module add1(clk,din1, din2, din3, dout,  cout);
    input clk;
    input [7:0] din1;
    input [7:0] din2;
    input       din3;
    output [7:0]dout;
    output      cout;
     
     reg [7:0] dout;
     reg       cout;
     
     always @(posedge clk) 
     begin
        {cout,dout} <= din1 + din2 + din3;
     end
endmodule

testbench如下：

verilog 复制代码

`timescale 1ns / 1ps
module test_add1;
    reg clk;
    reg [7:0] din1;
    reg [7:0] din2;
    reg       din3;
    wire [7:0]dout;
    wire      cout;
add1 add1u(
           .clk  (clk),
           .din1 (din1), 
           .din2 (din2), 
           .din3 (din3), 
           .dout (dout),  
           .cout (cout)
           );
initial
begin
clk=1;
end
always #5 clk=~clk;
initial
begin
din1=8'd0;
din2=8'd0;
din3=1'd0;
#10
din1=8'd2;
din2=8'd3;
din3=1'd0;
#10
din1=8'd4;
din2=8'd5;
din3=1'd0;
#10
din1=8'd8;
din2=8'd11;
din3=1'd1;
#10
din1=8'd18;
din2=8'd21;
din3=1'd1;
#10
din1=8'd22;
din2=8'd31;
din3=1'd1;
#10
din1=8'd0;
din2=8'd0;
din3=1'd0;
end
 
endmodule

仿真结果如下：

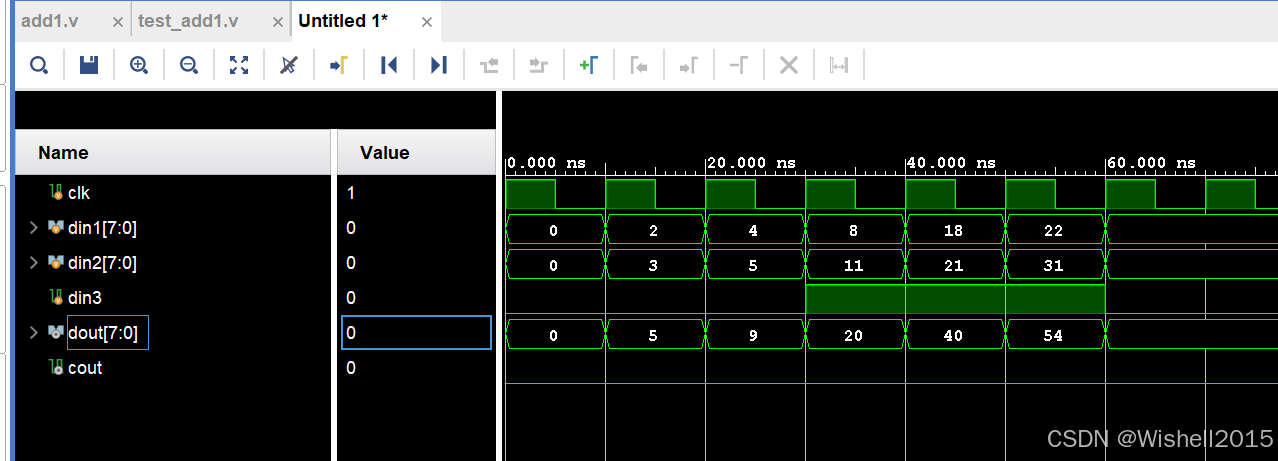
RTL结构图：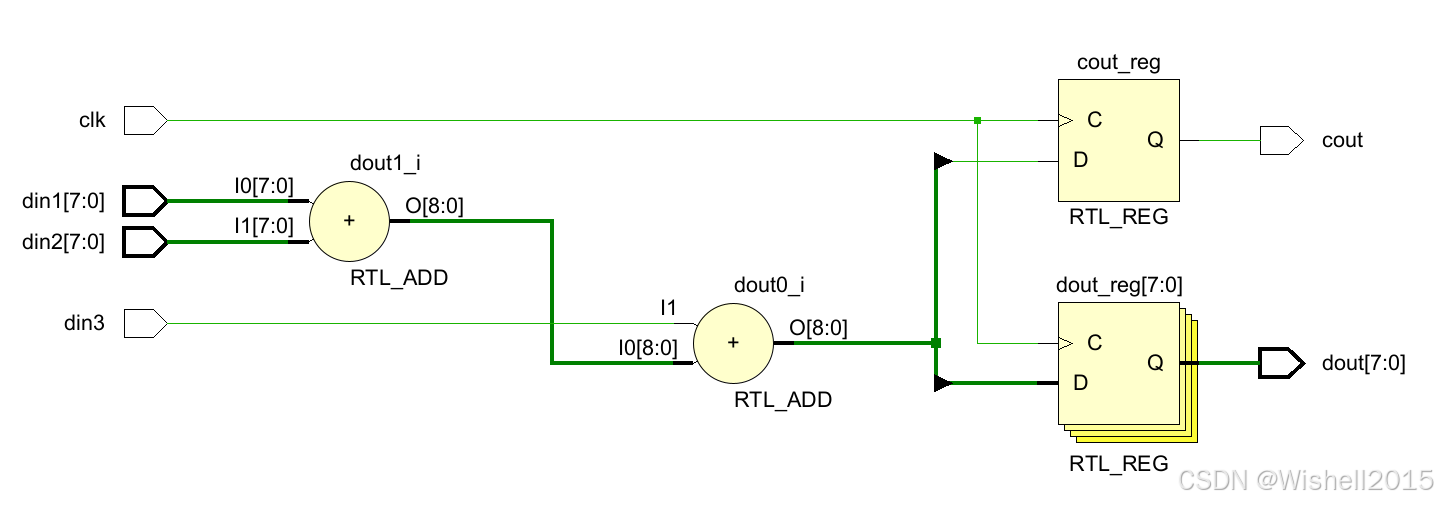

‍

采用流水线思想

verilog 复制代码

`timescale 1ns / 1ps
module add1_pipeline(
    input wire clk,
    input wire [7:0] din1,
    input wire [7:0] din2,
    input wire       din3,
    output reg [7:0] dout,
    output reg       cout
);

    // --- 第一级流水线寄存器 ---
    reg        cout_low_reg;   // 存储低4位的进位
    reg [3:0]  sum_low_reg;    // 存储低4位的和
    reg [3:0]  din1_high_reg;  // 【关键】存储高4位输入，用于数据对齐
    reg [3:0]  din2_high_reg;  // 【关键】存储高4位输入，用于数据对齐
    
    // --- 第一级流水线逻辑 ---
    always @(posedge clk) begin
        // 1. 计算低4位，产生进位和结果
        {cout_low_reg, sum_low_reg} <= din1[3:0] + din2[3:0] + din3;
        
        // 2. 【关键】同步缓存高4位数据，让它们晚一拍再参与运算
        din1_high_reg <= din1[7:4];
        din2_high_reg <= din2[7:4];
    end
     
    // --- 第二级流水线逻辑 ---
    always @(posedge clk) begin
        // 使用【缓存过的高位数据】和【上一级产生的进位】进行运算
        // 结果的高4位(含进位) 拼接 上一级的低4位结果
        {cout, dout[7:4]} <= din1_high_reg + din2_high_reg + cout_low_reg;
        
        // 低4位结果直接透传到输出（已经在流水线里待了一拍了）
        dout[3:0]         <= sum_low_reg;
    end

endmodule

流水线的RTL：

‍

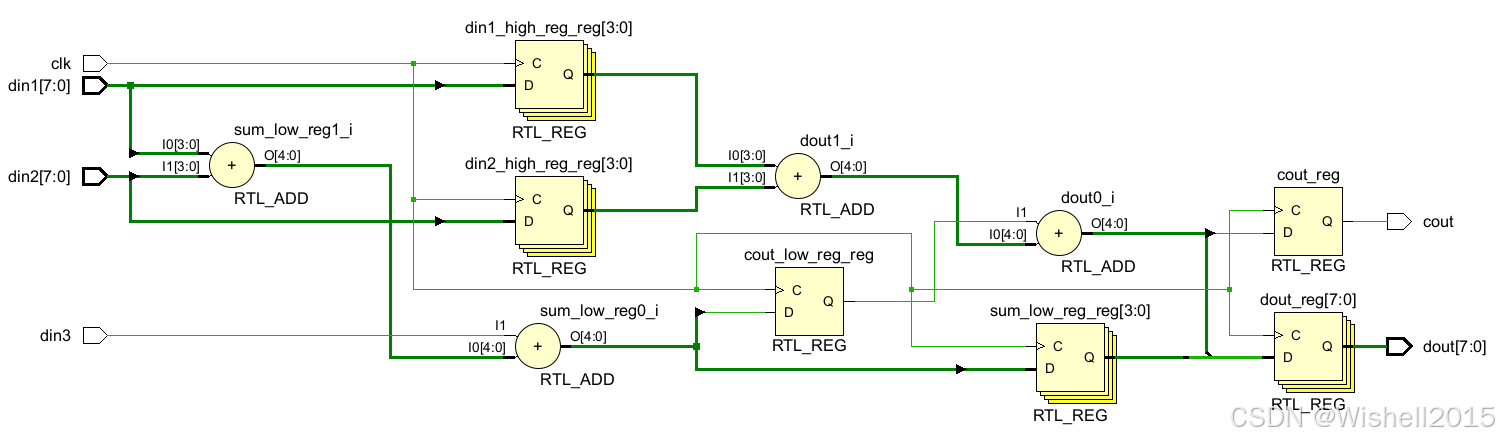
空间切分：把"大象"切成块

不要试图一口气做完所有事情。

非流水线：

逻辑：din1 + din2 + din3 （8位加法）。
这是一个"全能工匠"模式。在一个时钟周期内，电信号必须从最低位跑到最高位（进位链）。如果这个加法需要 10ns，时钟周期就必须大于 10ns（频率 < 100MHz）。这决定了系统的速度上限。

流水线：

逻辑：把 8位加法切成两个 4位加法。
这是"工厂流水线"模式。工位 1 ：只负责算低 4 位。工位 2 ：只负责算高 4 位。现在每个工位只需要算 4位加法，假设耗时变成 5ns。那么时钟周期可以缩短到 5ns（频率提升到 200MHz）。系统变快了！

时间同步

这是流水线最容易出错的地方。所有参与同一级运算的数据，必须来自同一个"时代"（同一个时钟周期）。

为了配合 cout_temp（它是上一拍数据的产物），原本的高位输入 din1[7:4] 必须等待。
我们需要给 din1[7:4] 安排一个"候车室"（寄存器），让它等一拍。
到了下一拍，cout_temp 出来了，候车室里的 din1_old 也出来了，它们才是"原配"，才能在一起运算。

核心格言：流水线不仅是切分逻辑，更是管理数据的"旅行时间"，确保它们在正确的时间点相遇。

效率权衡：吞吐率 vs 潜伏期

流水线不是免费的午餐，它用"等待"换来了"速度"。

潜伏期（Latency）变长了：

原代码：输入数据，1个周期后出结果。
流水线代码：输入数据，2个周期后才出结果。
代价：对于单个数据来说，处理时间变长了。

吞吐率（Throughput）变高了：

虽然第一个结果要等 2 个周期，但是从第 2 个周期开始，每个时钟周期都会蹦出一个新结果。
而且，因为主频翻倍了（100M -> 200M），每秒钟能处理的数据总量翻倍了！

假设输入两组数据：

T1 时刻输入 ：10 + 20 (Data A)
T2 时刻输入 ：30 + 40 (Data B)

流水线中，发生了什么？

时钟周期	阶段 1 (低4位处理)	阶段 1 附属动作 (高位缓存)	阶段 2 (高4位处理)	输出结果
T1	计算 `10+20` 的低4位	暂存 `10+20` 的高4位	(无效数据)	无效
T2	计算 `30+40` 的低4位	暂存 `30+40` 的高4位	取出 `10+20` 的高4位 + 低位进位	输出 10+20 的结果
T3	(处理 Data C...)	(暂存 Data C...)	取出 `30+40` 的高4位 + 低位进位	输出 30+40 的结

在 T2 时刻：电路的前半部分正在处理 Data B （新来的）。电路的后半部分正在处理 Data A（刚才剩下的）。

这就是流水线：不同的任务在同一时刻重叠执行。

总结：

心中有路（Path） ：看代码时，脑子里要能画出信号流动的路径。哪里是组合逻辑（跑得快但不能存），哪里是寄存器（跑得慢但能存）。
对齐意识（Alignment） ：永远盯着数据看，问自己："这个数据是哪一拍的？那个数据是哪一拍的？它们能相加吗？"如果辈分不同，就必须加寄存器打拍对齐。
切分艺术（Retiming） ：如果时序报告告诉你"路径太长、频率上不去"，就在那条长路径中间切一刀，插入一组寄存器。这就是流水线优化的本质。

‍