FPGA教程系列-流水线再看

FPGA教程系列-流水线再看

对于axis_register的进一步思考

经过一轮代码的洗礼，从最开始的加法器的流水线思想，到axis_register代码的解读，其实有点云里雾里了，忽然联系到了学习的三大境界：看山是山，看水是水----看山不是山，看水不是水----看山还是山，看水还是水。再重新对流水线思考一下。

代码里用generate分了三种模式，直连（​else​ ​），寄存器模式（​REG_TYPE == 1​ ​），以及Skid Buffer（REG_TYPE > 1）。

直连的弊端

回归一下，为什么要分这三种模式，直接进行直连不好吗？

答案是不好。从逻辑仿真（Functional Simulation）的角度来看，​ ​REG_TYPE=0​ ​ （直连/Bypass）确实是最完美的：

1. 零延迟：数据这一拍进，这一拍就出。
2. 零气泡：只要下游收，上游发，中间没有任何停顿。

既然 REG_TYPE=0​ 既快又没气泡，为什么还需要 REG_TYPE=2（Skid Buffer）搞得这么复杂呢？

答案不在于"逻辑波形"，而在于物理时序（Timing）和最高运行频率（Fmax） 。

1. 致命伤：无限延长的组合逻辑链

设想一下，在 FPGA 里串联了 5 个处理模块（Module A -> B -> C -> D -> E），每个模块如果都用 REG_TYPE=0：

• Valid 路径 ：Source 发出的 Valid 信号，必须在同一个时钟周期内，像电流一样瞬间穿过 A, B, C, D，最后到达 E。
• Ready 路径（更致命） ：E 发出的 Ready 信号，必须在同一个时钟周期内，反向穿过 D, C, B, A，最后告诉 Source。

这条路径上的组合逻辑延迟（Gate Delay + Routing Delay）会累加。

Ttotal=Tlogic_A+Tlogic_B+⋯+Tlogic_E T_{total} = T_{logic\A} + T{logic\B} + \dots + T{logic\_E} Ttotal=Tlogic_A+Tlogic_B+⋯+Tlogic_E

如果这个总延迟超过了时钟周期（比如 200MHz 时钟，周期只有 5ns），时序分析（Timing Analysis）就会报错（Setup Violation）， FPGA 跑不到预期的频率，或者编译失败。

增加寄存器，提高工作频率-流水线

1. 什么是"最长路径" (Critical Path)？

在 FPGA 中，数据在一个时钟周期内，必须完成以下动作：

1. 出发：从源寄存器（Source Reg）发射出来（T_co）。
2. 跑路：经过中间的一堆组合逻辑（加法器、多路选择器、LUT等）和长长的导线（T_logic + T_routing）。
3. 到达 ：在下一个时钟沿到来之前，稳定地到达目的寄存器（Dest Reg）的门口（T_setup）。

关键规则：时钟周期必须比这个过程的总耗时要长，否则数据还没跑完，大门（时钟沿）就关了，数据就错了（Timing Violation）。

2. 具体算笔账：切蛋糕原理

假设有一个复杂的逻辑模块，如果不加寄存器，数据要一口气跑完 3 个逻辑块（A、B、C）。

场景一：不加寄存器（Bypass ）

路径：Reg_Src →\rightarrow→ [逻辑A (3ns)] →\rightarrow→ [逻辑B (3ns)] →\rightarrow→ [逻辑C (3ns)] →\rightarrow→ Reg_Dst

• ​总耗时（路径长度） ：3+3+3=9ns3 + 3 + 3 = 9ns3+3+3=9ns。

• ​时钟周期要求：必须大于 9ns。

• 最高频率 ：

  Fmax=19ns≈111 MHz F_{max} = \frac{1}{9ns} \approx 111 \text{ MHz} Fmax=9ns1≈111 MHz

这意味着，哪怕逻辑 A 和 B 跑得很快，整个系统也必须等待数据跑完 C，才能进行下一轮。

---

场景二：中间切一刀（插入寄存器 ）

在逻辑 B 和逻辑 C 之间插入一个寄存器，路径变成了两条独立的短跑道：

1. ​路径 1 ​：Reg_Src →\rightarrow→ [逻辑A (3ns)] →\rightarrow→ [逻辑B (3ns)] →\rightarrow→ Reg_Mid

   耗时：3+3=6ns3 + 3 = 6ns3+3=6ns

2. ​路径 2 ​：Reg_Mid →\rightarrow→ [逻辑C (3ns)] →\rightarrow→ Reg_Dst

   耗时：3ns3ns3ns

现在的瓶颈在哪里？系统的速度取决于最慢的那条路（Critical Path）。在这里，最慢的是路径 1（6ns）。

• ​新的最长路径：6ns。

• ​时钟周期要求：只要大于 6ns 即可（不需要管路径 2，因为它跑得快，有足够的时间休息等待时钟）。

• 最高频率 ：

  Fmax=16ns≈166 MHz F_{max} = \frac{1}{6ns} \approx 166 \text{ MHz} Fmax=6ns1≈166 MHz

结果： 频率从 111 MHz 提升到了 166 MHz，性能提升了 50%！

---

3. 如果切得更细呢？（Pipeline Level）

如果做得更极致，在逻辑 A 和 B 之间也插入寄存器：

1. 路径 1：Reg →\rightarrow→ A (3ns) →\rightarrow→ Reg
2. 路径 2：Reg →\rightarrow→ B (3ns) →\rightarrow→ Reg
3. 路径 3：Reg →\rightarrow→ C (3ns) →\rightarrow→ Reg

最长路径变成了 3ns。

Fmax=13ns≈333 MHz F_{max} = \frac{1}{3ns} \approx 333 \text{ MHz} Fmax=3ns1≈333 MHz

频率翻了 3 倍！

通过物理截断，减少了任意两个寄存器之间的组合逻辑延时（Logic Delay）和布线延时（Routing Delay），从而允许时钟翻转得更快。

去除反压与气泡

结合代码看：REG_TYPE=1 为什么会产生气泡？对比一下 Type 1 (普通寄存器) 和 Type 2 (Skid Buffer) 在面对"反压恢复"时的表现。

场景：下游堵住了一会儿，突然通了。

Type 1 (普通寄存器) ------ 有气泡

就像一个单座的房间。

1. 堵住时：房间里坐着客人 A（数据），想出去但门关着（下游不 Ready）。门外站着客人 B（上游新数据），想进进不来（因为房间满了，上游 Ready 也拉低）。
2. 恢复时：下游门开了。
3. 动作 1：客人 A 走出房间。
4. 动作 2 ：此时房间空了，上游才看到"哦，房间空了（Ready 拉高）"，然后才让客人 B 走进来。
5. 结果 ：在 A 走后、B 进来前，房间是空的。对于下游来说，它收到了 A，然后等了一拍（气泡），才收到 B。

Type 2 (Skid Buffer) ------ 无气泡

就像一个带等候区的房间（主寄存器 + 备用寄存器）。

1. 堵住时：主座位坐着客人 A，等候区站着客人 B。上游被告知满了。
2. 恢复时：下游门开了。
3. 动作 ：客人 A 立即走出的同时 ，等候区的客人 B 瞬间补位坐到了主座位上。
4. 结果 ：下游看到的是 A 刚走，B 马上就来了。中间没有空隙。上游随后再往等候区塞客人 C。

REG_TYPE=2 的伟大之处，就是它用多消耗一点点资源（那个备用的等候区）的代价，消灭了那个气泡。

仿真

可以针对alex的模块编写一个仿真程序。

REG_TYPE = 0 (Bypass)

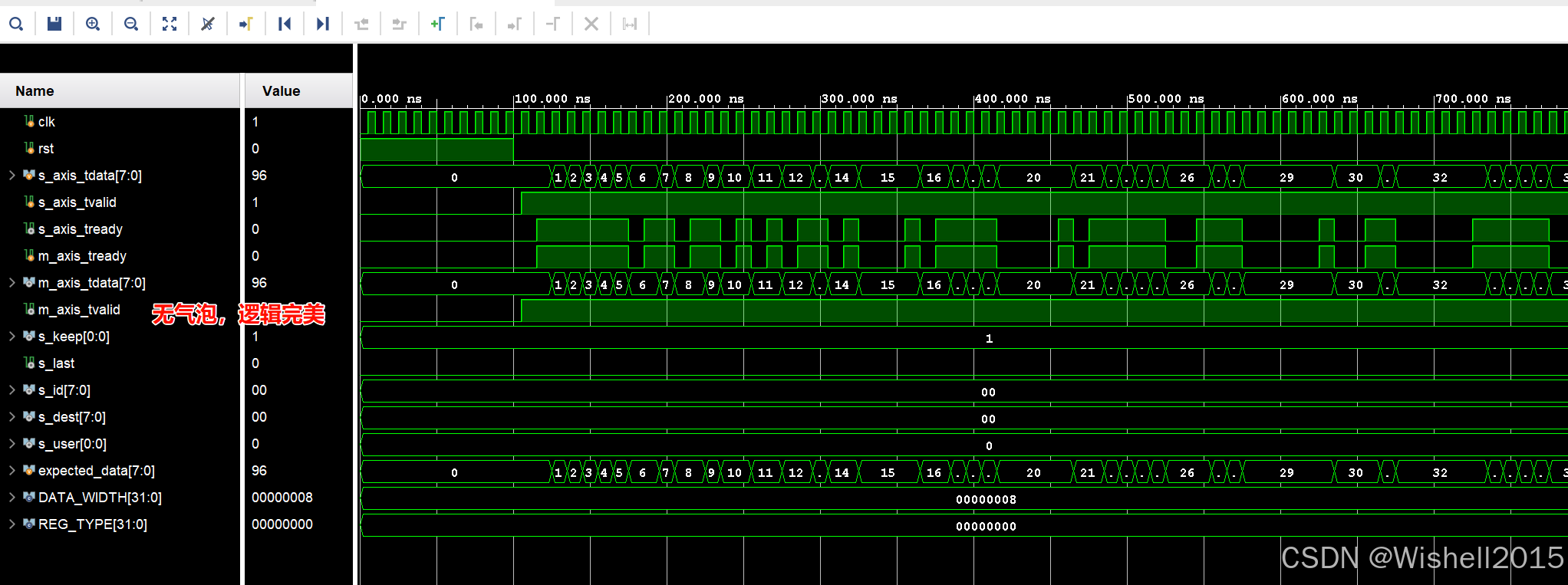
REG_TYPE = 1 (Simple)

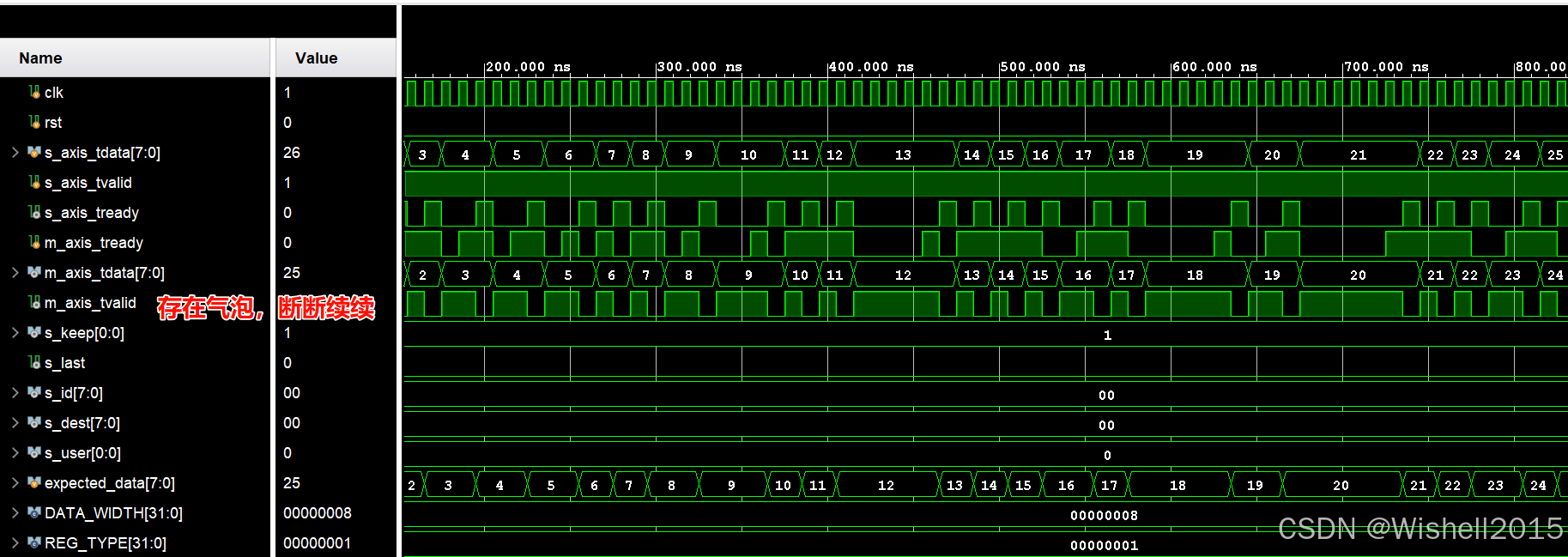
REG_TYPE = 2 (Skid Buffer)

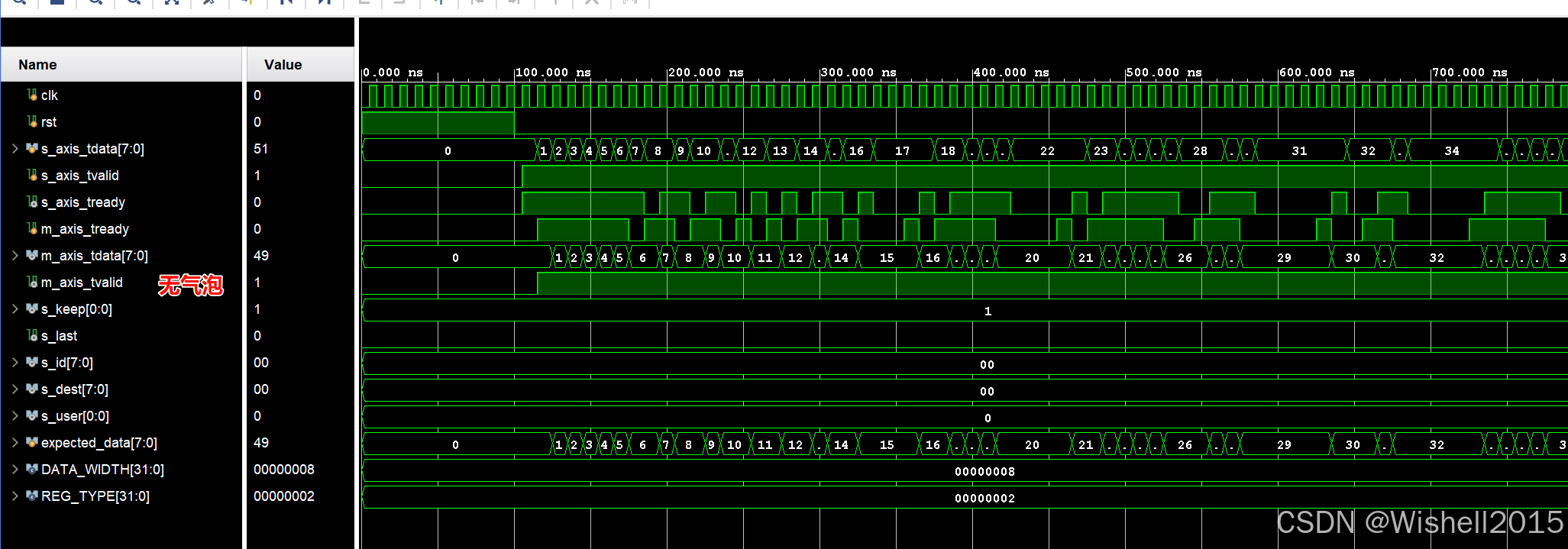
特性	REG_TYPE = 0 (Bypass)	REG_TYPE = 1 (Simple)	REG_TYPE = 2 (Skid Buffer)
是否有气泡	无(满带宽)	有(反压恢复时可能丢 50% 带宽)	无(满带宽)
逻辑延迟	0 Cycle	1 Cycle	1 Cycle
时序路径	透传 (最差) 上下游组合逻辑直连	切断 (好) Ready 信号被切断	完全切断 (最好) Valid/Ready/Data 全被切断
资源消耗	0 (仅连线)	低 (1级寄存器)	中 (2级寄存器)
适用场景	简单的模块内连接，逻辑极短	对带宽不敏感，只想改善时序	高性能总线，既要高频又要满带宽

‍

‍

‍