摘要
稀疏专家模型是一个已有三十年历史的概念，如今正重新成为深度学习领域的热门架构。这类架构涵盖混合专家模型、Switch Transformer 模型、路由网络、BASE 层等诸多模型，其核心统一思想为：每个样本仅由参数集合中的一个子集进行处理。借助这一设计思路，稀疏度实现了参数规模与单样本计算量的解耦，由此能够构建出参数体量极大但计算效率出众的模型。此类模型已在自然语言处理、计算机视觉、语音识别等多个领域展现出显著的性能提升。本文对稀疏专家模型的概念进行综述，对主流算法进行基础阐述，梳理其在深度学习时代的技术发展脉络，并最终指明未来的研究方向。
1.引言
机器学习领域，尤其是自然语言处理方向，通过提升计算资源投入、扩充训练数据以及增大模型规模，取得了令人瞩目的进展。具有里程碑意义的代表性语言模型包括 GPT-2（拉德福德等人，2018）、BERT（德夫林等人，2018）、T5（拉菲尔等人，2019）、GPT-3（布朗等人，2020）、Gopher（雷等人，2021）、Chinchilla（霍夫曼等人，2022）以及 PaLM（乔德里等人，2022）。
然而，当前性能处于领先水平的模型，往往需要数千台专用互联加速器持续运行数周乃至数月。这使得此类模型的研发成本高昂，并且会产生巨额的能源消耗（帕特森等人，2021）。因此，随着机器学习系统规模的不断扩大，该领域亟需探索更高效的训练与部署范式。而稀疏专家模型，正是在此背景下应运而生的一种极具潜力的解决方案。（state-of-the-art models ：译为性能处于领先水平的模型，serving paradigms ：译为部署范式）
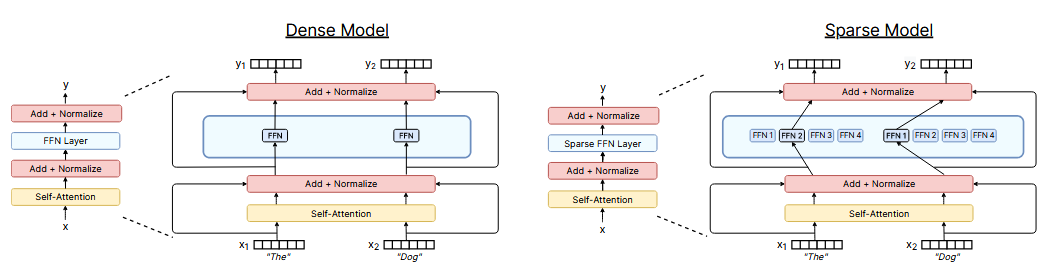
图 1：稠密 Transformer 与稀疏专家 Transformer 的对比 左侧的稠密模型会将所有输入 token 送入同一组前馈网络（FFN）参数 进行处理；右侧的稀疏专家模型则会为每个输入 token 独立选择四个专家网络（FFN1......FFN4）中的部分网络执行计算。** ****需要说明的是，本图中两个模型的计算量相近**。此外，尽管本图展示的是 Transformer（瓦斯瓦尼等人，2017）中稀疏前馈网络层的一种常用典型方案，但该技术的适用场景具有更强的通用性。
稀疏专家模型是一类将参数集合划分为若干个 **"专家网络"的神经网络，每个专家网络都拥有独立的权重参数，其中混合专家模型（MoE）** 是该类模型中最主流的变体。
在训练与推理阶段，模型会将输入样本分配至特定的一个或多个专家网络的权重参数中。因此，每个样本仅会与网络参数的一个子集发生交互，这与传统模型中每个输入都要调用全部网络参数的做法形成鲜明对比。由于处理每个样本时仅会启用一部分专家网络，相较于模型的总参数量，其实际产生的计算量仍可保持在较低水平。
许多现代稀疏专家模型的设计灵感均源于沙泽尔等人的研究（2017）------ 该研究团队在当时训练出了规模最大的模型，并在语言建模与机器翻译任务上取得了业界领先的性能表现 。当稀疏专家模型与 Transformer 语言模型相结合后，其受欢迎程度进一步攀升（列皮欣等人，2020；费杜斯等人，2021）。尽管相关研究工作大多集中于自然语言处理领域，但这类模型也已成功应用于计算机视觉（普伊塞尔韦等人，2020）、语音识别（尤等人，2021）以及多模态学习（穆斯塔法等人，2022）等多个领域。克拉克等人的近期研究（2022），针对不同模型规模与专家数量下稀疏专家模型的缩放特性 展开了严谨的探究。此外，目前诸多基准测试任务的最优结果 均由稀疏专家模型创造，例如 ST-MoE 模型（佐夫等人，2022）。随着相关研究与工程技术的不断进步，人们对稀疏专家模型的认知持续加深，其实验性能也稳步提升，该领域正处于快速发展阶段。（scaling properties 译为缩放特性 ，empirical results 译为实验性能）
我们将本次综述的范围限定于深度学习时代 （大致为 2012 年至今）的稀疏专家模型，梳理该领域的近期研究进展，并探讨其极具潜力的未来发展方向。若读者希望全面了解混合专家模型在深度学习兴起之前的发展历史，可参考综述文献《混合专家模型二十年》（尤克塞尔等人，2012）。此外，稀疏专家模型可被视为自适应计算模型 的一个特殊类别，相关综述可查阅徐与麦考利的研究成果（2022）。最后，泰伊等人（2020）的综述涵盖了一系列旨在提升 Transformer 计算效率的方法，而稀疏专家模型正是其中一种极具前景的技术方案。（（heuristically 2012 onward译为大致为 2012 年至今，recounting recent advances and discussing promising future avenues采用 "梳理...... 进展，并探讨...... 发展方向）
2.稀疏专家模型
机器学习领域中混合专家模型（MoE）的概念最早可追溯至至少三十年前，相关开创性研究见于雅各布斯等人（1991）以及乔丹与雅各布斯（1994）的成果。在早期概念中，每个 "专家" 指代一整个独立的神经网络，彼时的混合专家模型与集成学习方法的原理较为相近。（ensemble methods ：译为集成学习方法）
2.1 深度学习领域中的应用
艾根等人（2013）提出了一种架构，该架构在经过扰动处理的 MNIST 数据集（勒丘恩等人，1998）上采用了堆叠式混合专家层。这项研究采用的是专家输出的连续混合策略（软选择） ，而非在每一层都仅选取表现最优的部分专家（硬选择）------ 这一设计限制了模型的实际应用价值 ¹。尽管如此，该研究为后续混合专家模型作为神经网络组件的高效实现方案奠定了基础。深度学习领域中，这种方法的首次大规模成功实践来自沙泽尔等人（2017）的研究。该团队在两层长短期记忆网络（LSTM，霍克赖特与施密德胡伯，1997）之间嵌入了一个混合专家层，将下层长短期记忆网络的输出送入混合专家层中进行计算。最终得到的稀疏模型在机器翻译任务上达到了业界领先水平 ，不过其中参数量达 1370 亿、包含 131,072 个专家网络的最大变体，其泛化性能反而不如更小的模型变体。尽管取得了上述成果，但后续相关研究却进入了相对沉寂的阶段，研究重心更多转向了对 Transformer 模型（瓦斯瓦尼等人，2017）的直接探索。这种局面随着 GShard（列皮欣等人，2020）与 Switch Transformer（费杜斯等人，2021）的问世发生了改变 ------ 这两项研究均采用专家层替代了 Transformer 架构中的前馈网络层。不过，虽然 **"专家层" 方案 ** 已成为当前的主流范式，但近期也有研究重新审视了 "专家为完全独立模型" 这一早期概念（古鲁兰甘等人，2021；李等人，2022）。这种设计具备模块化与可组合性的优势：李等人（2022）的研究表明，可通过组合针对特定领域训练的专家语言模型，来构建定制化网络。（jittered MNIST ：译为经过扰动处理的 MNIST 数据集 ，"jitter" 在机器学习数据预处理语境中表示对数据添加微小扰动以提升模型鲁棒性）（soft selection / hard selection ：译为软选择 / 硬选择 ，是稀疏专家模型领域的标准术语，分别对应 "连续混合所有专家输出" 和 "仅选取 Top-K 专家参与计算" 的策略。）（set the stage for ：译为为...... 奠定了基础 ）（follow-on research was relatively dormant ：译为后续相关研究却进入了相对沉寂的阶段，"dormant" 准确对应研究热度消退的状态。）
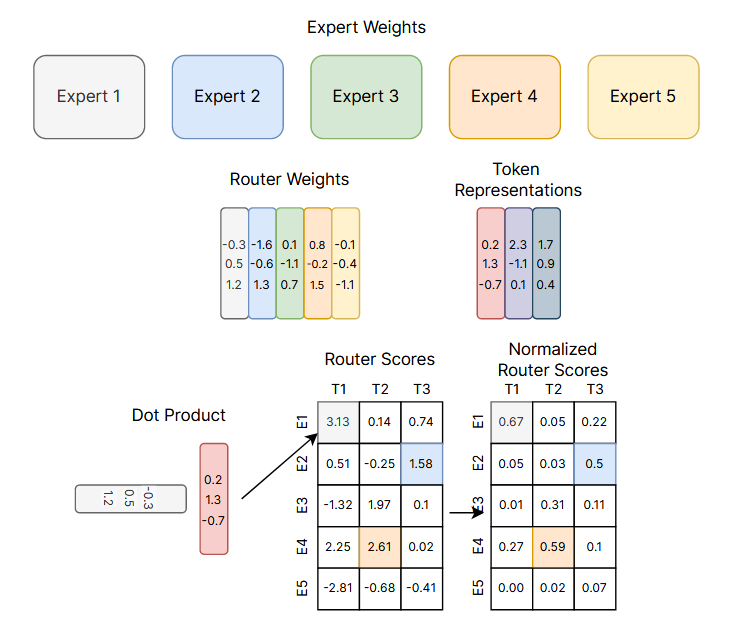
图 2：Top-K 路由机制示意图 本图展示了在5 个专家网络 与3 个输入 Token 上执行 Top-K Token 路由策略的示例。每个专家网络与 Token 均采用颜色编码进行区分，路由权重（Wr）为每个专家网络都配置了对应的特征表示（与颜色一一匹配）。在路由决策阶段，路由权重会与每个 Token 的嵌入向量（x）执行点积运算，生成路由得分（h(x)）；随后对这些得分进行归一化处理，使其求和结果为 1，得到最终的概率分布（p(x)）。（top-k routing ：译为 Top-K 路由机制，dot product ：译为 点积运算）
图 2 展示了沙泽尔等人（2017）提出的原始 Top-K 路由机制，该机制为后续诸多相关研究奠定了基础 。路由算法的最新改进将在第 4 节中阐述。基于输入内容选择专家网络的操作，通常需要执行离散选择 （即确定启用哪一个专家网络），而这会给依赖可微性的反向传播算法带来难题。为解决这一问题，沙泽尔等人（2017）提出了一种 Top-K 路由函数：该函数以 Token 表征向量x作为输入，随后将其分配给包含N个专家网络的集合{Ei}i=1N中排名前K的专家网络。路由模块包含一个可训练参数Wr，该参数用于计算对数几率值 h(x)=Wr⋅x；之后通过 Softmax 函数对该对数几率值在N个专家网络上进行归一化处理。专家网络i对应的门控值计算公式如下：（foundational to many follow-on works 译为为后续诸多相关研究奠定了基础，discrete selection 译为离散选择，complicates backpropagation algorithms relying on differentiability 拆解为会给依赖可微性的反向传播算法带来难题）
我们将选中的前 K 个专家网络的索引集合 记为 T。该网络层的输出计算方式为：以门控值作为权重，对每个专家网络基于该 Token 完成的计算结果进行线性加权组合 。（selected top-k expert indices 译为前 K 个专家网络的索引集合，by the gate value 译为以门控值作为权重）
需要说明的是，与艾根等人（2013）的研究不同，本方法仅会选取排名前 K 的专家网络 参与计算，因此计算效率更高。（in contrast to ：译为与...... 不同，this selection is only over the top-k experts ：译为仅会选取排名前 K 的专家网络参与计算，computationally efficient ：译为计算效率更高）
2.2 面向现代硬件的适配设计
现代稀疏专家模型的研发过程，与用于训练超大神经网络的分布式系统协同推进 。此类模型属于稀疏神经网络的一个特殊分支（盖尔等人，2019；德特默斯与策特尔莫耶尔，2019；埃夫奇等人，2020）------ 二者的共性在于均仅调用部分参数参与计算，区别则在于稀疏专家模型的稀疏模式可能具备非规则性 。尽管通用型稀疏神经网络（采用非规则稀疏模式）在理论上能够降低浮点运算总量（FLOPs），但当前硬件的设计初衷是针对连续（规则）内存块 执行线性代数运算，因此往往无法高效支持这类非规则稀疏模型的运行。与之不同的是，稀疏专家模型激活的是完整的参数块 （即完整的矩阵），因此能够在现代硬件上，将理论层面的浮点运算量节省，切实转化为实际的训练耗时缩减（费杜斯等人，2021；拉吉班达里等人，2022）。（co-designed 译为协同推进，irregular sparsity patterns 译为非规则稀疏模式，）
为了训练规模最大的神经网络，模型的各类数据（如权重、激活值、优化器变量）会通过多种并行策略进行分片处理。三种常用的并行方法包括：数据并行 （模型权重保持完整，训练数据进行分片）、张量模型并行 （沙泽尔等人，2018）（数据张量与权重张量均在多个计算设备间拆分），以及流水线并行 （哈勒普等人，2018；黄等人，2019）（将完整的网络层或网络层组分配到不同计算设备上）。混合专家模型与这些并行方案的适配性极佳。各个专家网络部署在不同的加速器上，输入数据则被动态分发至对应专家网络，并取回计算结果。早期的混合专家架构通常会采用大量体量较小的专家网络，单个专家网络即可完整放入一台加速器中（列皮欣等人，2020）；而后续的相关研究则设计了体量更大的专家网络，这类大专家网络必须拆分到多台加速器上运行（费杜斯等人，2021；杜等人，2021），同时还需要针对性的额外优化手段来提升通信效率（沙泽尔等人，2018；罗伯茨等人，2022；拉吉班达里等人，2022）。（sharded 译为分片处理，data parallelism / tensor model-parallelism / pipeline parallelism 分别译为数据并行 / 张量模型并行 / 流水线并行，fit naturally with 译为适配性极佳，）
与标准 Transformer 模型相比，分布式系统上的动态路由 会产生额外的通信开销。将输入分发至专家网络的操作，通常通过全对全（all2all）通信原语 实现 ------ 在该机制下，每一台加速器都会与其他所有加速器进行数据通信 ²。容量因子 会通过调节专家网络的批次大小来直接影响通信成本，其计算公式为 CF⋅(B/E)，其中 CF 代表容量因子，B 为每一批次的总 Token 数，E 为专家网络的数量。容量因子的取值越大，模型性能往往越优，但代价是通信、内存与计算成本的同步上升。通过对全对全通信原语的高效实现，以及对路由算法的改进（例如降低容量因子的取值），能够有效缓解稀疏专家算法带来的额外通信成本。（all2all communication primitive 译为全对全（all2all）通信原语）
在训练常规分布式 Transformer 模型时，每台加速器将要处理的批次数据是预先确定 的。然而，动态路由算法会打破这一特性 ------ 由于输入数据会被动态分配至各个专家网络，往往会导致发送到每个专家网络的输入数据量各不相同 。因此，路由算法通常需要促进各加速器之间的负载均衡 ，以保障硬件的高效利用率。实现负载均衡的方式包括引入辅助损失函数（沙泽尔等人，2017），以及将该问题转化为线性分配问题进行求解（刘易斯等人，2021；克拉克等人，2022）。有关负载均衡技术的进一步改进细节，详见本文第 4 节。（break this property 译为打破这一特性，load balance over the accelerators 译为各加速器之间的负载均衡，）
最后，近期在系统层面的技术进展 ，进一步优化了混合专家模型（MoE）的训练与部署流程。亚斯丘尔等人（2021）对 Transformer 模型的所有网络层（包括稠密层与自注意力层）进行了稀疏化改造，在单样本推理（无批次处理）这一特殊场景下，实现了高达 37 倍的推理速度提升。科斯曼等人（2022）依托 RECOMPILE 程序库，突破了专家网络批次大小固定的限制。该系统可对混合专家模型的计算资源进行动态重编译与优化 ，使张量维度能够匹配专家网络的实时计算需求，而非局限于静态设定的数组规模。此外，除了数据并行、模型并行与专家并行这三种范式外，DeepSpeed-MoE 程序库（拉吉班达里等人，2022）还支持零冗余优化器（ZeRO）分片技术 （拉吉班达里等人，2019）------ 即对张量进行完全分片，并按需重新聚合，同时也支持零冗余优化器卸载（ZeRO-Offload）技术 ，通过将部分计算任务卸载至 CPU 来降低 GPU 的内存占用。该系统不仅实现了 10 倍的推理性能提升（拉吉班达里等人，2022），还在机器翻译任务上取得了业界领先的效果（金等人，2021），显著增强了这类模型在实际生产环境中部署应用的可行性。（systems advances 译为系统层面的技术进展，sparsify all the layers 译为进行了稀疏化改造，relax the constraints 译为突破了...... 的限制，ZeRO partitioning / ZeRO-Offload 采用领域通用译法零冗余优化器（ZeRO）分片技术 / 零冗余优化器卸载（ZeRO-Offload）技术）
3 稀疏专家模型的缩放特性
研究表明，在不受参数规模、数据量与计算资源三者中另外两项因素约束的前提下，稠密神经语言模型的交叉熵损失会随模型参数总量、数据量以及计算资源投入量呈现幂律缩放关系 （即对于变量 x，满足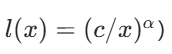
（卡普兰等人，2020）。霍夫曼等人（2022）后续修正了该幂律关系的系数，其研究证实，计算最优模型 需要在数据量与参数规模的缩放之间实现更精细的平衡。与之不同的是，稀疏专家模型的早期相关研究多采用经验性的缩放策略 ------ 这类策略虽取得了优异的实验结果，但并未对模型的缩放规律进行严谨的刻画。此外，多项研究指出，稀疏专家模型在上游任务 （如预训练）与下游任务 （如微调）中的表现存在差异（费杜斯等人，2021；阿特克塞等人，2021），这进一步加大了理解与阐释稀疏专家模型的难度。（scaling properties 译为缩放特性，power-law 译为幂律缩放关系，compute budget 译为计算资源投入量，upstream / downstream 译为上游任务 / 下游任务，heuristically 译为经验性的）
3.1 上游任务缩放特性
稀疏专家模型在大规模数据集上训练时表现卓越。自然语言处理领域的一种通用范式是：先开展上游任务训练（如预训练），再针对特定关注的数据分布进行下游任务训练（如微调）。在上游训练阶段 ，稀疏专家模型相较稠密模型，始终能取得更为显著的性能提升。沙泽尔等人（2017）在10 亿词语言建模基准测试集 （切尔巴等人，2013）上，绘制了模型性能随参数规模与计算资源投入量变化的缩放曲线，所提模型相较稠密版本实现了大幅性能跃升。列皮欣等人（2020）研究了翻译性能随模型规模变化的规律，其参数量达 6000 亿的最大规模稀疏模型，实现了 13.5 个 BLEU 值的性能提升。Switch Transformer 模型（费杜斯等人，2021）在相同计算资源条件下，相较 T5 模型实现了 4 至 7 倍的实际训练时长 加速。该研究同时探究了交叉熵损失随参数总量变化的缩放规律，但发现当专家数量达到 256 及以上时，模型的性能提升幅度会逐渐衰减。（upstream scaling 译为上游任务缩放特性，wall-time 译为实际训练时长，gains diminished with 256+ experts 译为当专家数量达到 256 及以上时，模型的性能提升幅度会逐渐衰减）
为进一步深化相关认知，阿特克塞等人（2021）区分了混合专家模型（MoE）在域内数据 与域外数据 上的上游任务缩放表现，研究发现：该类模型在域内语言建模任务中的缩放效果显著优于稠密模型。这一结论也印证了费杜斯等人（2021）所指出的模型迁移难题 。（in-domain / out-of-domain data 译为域内数据 / 域外数据，corroborating the difficulties of transfer 译为印证了...... 模型迁移难题）
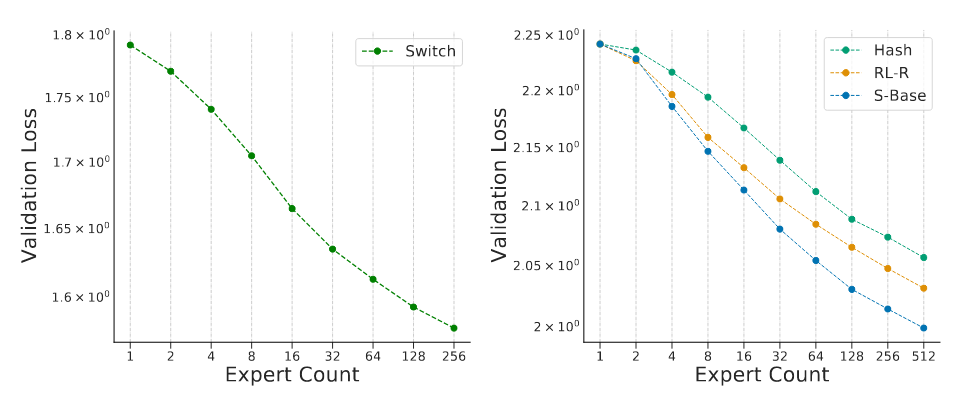
图 3：随专家数量变化的稀疏模型缩放特性曲线图 左图为费杜斯等人（2021）所呈现的交叉熵损失随专家数量变化的缩放曲线 ，右图则展示了克拉克等人（2022）提出的三种稀疏模型变体（S-Base、RL-R、Hash）的相关曲线。两张图中左上角的首个数据点 ，均对应一个与稀疏模型计算量匹配的稠密模型。随着专家数量的增加，模型的稀疏程度不断提升，验证集损失也随之降低。（sparse scaling plots with expert count 译为随专家数量变化的稀疏模型缩放特性曲线图，as a function of the number of experts 译为随专家数量变化的，the three sparse variants 译为三种稀疏模型变体，yield lower validation losses 译为验证集损失也随之降低）
在取得上述早期实验成果后，克拉克等人（2022）首次开展了大规模研究，旨在从数学层面刻画稀疏专家模型的缩放特性。该研究选取了三类稀疏模型，并推导提出了 ** 有效参数量（EPC）** 的概念。有效参数量基于浮点运算量（FLOPs）与专家数量，对稀疏专家模型对应的等效稠密模型参数量进行估算。这一概念的推导基于 "稀疏专家模型的损失函数遵循双线性特性" 这一假设；同时实验结果表明，交叉熵损失随该变量的变化同样符合幂律关系。图 3 左侧展示了 Switch Transformer 模型的交叉熵损失缩放曲线，右侧则呈现了克拉克等人（2022）提出的三种稀疏模型变体的相关曲线。（mathematically characterize 译为从数学层面刻画，effective parameter count (EPC) 译为有效参数量（EPC），conjecturing that 译为基于...... 这一假设，bilinear loss 译为双线性特性）
这些缩放曲线的一个核心特征在于：稀疏专家模型的性能增益会随模型规模的扩大而衰减 。经外推分析可得，当模型浮点运算量对应的参数量超过 9000 亿时，稀疏化设计将不再带来额外收益。不过，这一结论的成立依赖于训练所用的 Token 总量 ------ 该研究中所有模型的训练 Token 量均仅为 1300 亿。但参考霍夫曼等人（2022）近期发布的缩放规律研究结论（该研究建议使用更多 Token 来训练计算最优模型，例如奇奇拉模型就是一个参数量 700 亿、训练 Token 量达 1.4 万亿的模型），未来的相关研究或许可以重新审视这一分析结果。（the gain of sparse expert models decreased with scale 译为稀疏专家模型的性能增益会随模型规模的扩大而衰减，when extrapolated 译为经外推分析可得，in light of 译为参考）
3.2 下游任务缩放特性
然而，稀疏专家模型在上游任务 中稳定的缩放增益，并未直接转化为下游任务上的持续性能提升。在一项聚焦迁移难题 的研究中，费杜斯等人（2021）发现：一款低算力、高参数的编解码结构 Transformer 模型（参数量达 1.6 万亿，每个稀疏层配备 2048 个专家网络）在预训练阶段实现了 4 倍的性能提升，但在 SuperGLUE 这类强推理需求的任务（王等人，2019）上微调时，其表现却显著逊色于稠密模型。这一发现表明，相关领域仍需开展更深层次的研究，同时也暗示了计算量与参数量之间或许需要达成某种平衡 。不过，很快便有研究在少样本推理、微调以及其他模态任务中，取得了亮眼的实验结果。（reliable upstream scaling 译为上游任务中稳定的缩放增益，reasoning-heavy tasks 译为强推理需求的任务，strong empirical results 译为亮眼的实验结果）
杜等人（2021）探究了稀疏 GLaM 模型 的缩放特性，该系列模型的浮点运算量区间为 10 亿至 640 亿，且每个稀疏层均配备 64 个专家网络。GLaM 模型取得了业界领先的性能表现 ，在零样本与单样本任务上的效果超越了参数量达 1750 亿的 GPT-3 模型（布朗等人，2020）；同时，其推理阶段的单 Token 浮点运算量降低了 49%，能耗也减少了 65%（见图 4 左图）。稀疏模型在少样本推理任务上同样表现优异，另一项例证来自 BIG-Bench 基准测试的协作研究（斯里瓦斯塔瓦等人，2022）：在该基准包含的 161 个提交类 JSON 任务中，稀疏模型的性能相较稠密模型提升了一倍（见图 4 右图）。（ranging from 1B-64B FLOPs 译为浮点运算量区间为 10 亿至 640 亿，the 161 contributed JSON tasks 译为161 个提交类 JSON 任务）
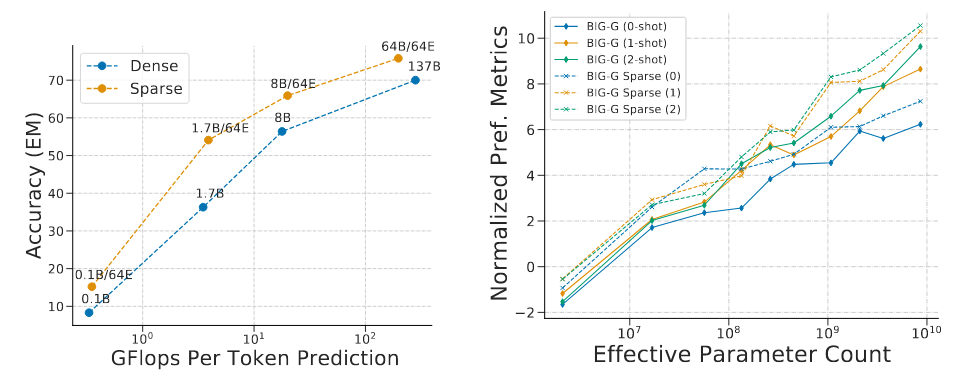
图 4：稀疏模型的少样本推理缩放特性 左图：杜等人（2021）在 TriviaQA 数据集上测试了模型的少样本推理性能，结果表明，在参数量不超过 1370 亿的区间内，稀疏混合专家模型相较稠密模型的性能优势始终稳定存在。图中每个标签（例如 8B/64E）代表模型单输入所用的参数量（80 亿）与专家网络数量（64 个） 。右图：BIG-Bench 基准测试项目（斯里瓦斯塔瓦等人，2022）在包含 161 个提交类 JSON 任务的更大规模数据集上，对模型的少样本缩放特性开展研究，验证了稀疏专家模型相较浮点运算量匹配的稠密模型 具备性能优势。（up to 137B parameters 译为参数量不超过 1370 亿的区间内，8B/64E 结合上下文译为80 亿参数量 / 64 个专家网络）
最后，斯里瓦斯塔瓦等人（2022）针对 BIG-Bench 基准测试中的选择题任务，开展了稀疏模型校准性能 的研究。校准用于衡量模型预测概率与预测正确率的匹配程度。该研究采用期望校准误差（Expected Calibration Error, ECE） （奈伊尼等人，2015）作为校准性能的衡量指标，这一指标的计算方式为：先按照预测概率对样本进行分组，再计算各组的预测概率与平均准确率之间的绝对偏差。研究发现，无论是更大规模的稠密模型还是稀疏模型，其校准性能均会随模型规模提升而优化（见图 5）；且稀疏模型能够达到的校准水平，与浮点运算量高出其 10 倍的稠密模型 相当。（calibration 译为校准，binning examples by their predicted probability 译为按照预测概率对样本进行分组 ，"binning" 在机器学习评价语境中对应 "分组 / 分箱" 操作，binning examples by their predicted probability 译为按照预测概率对样本进行分组，"binning" 在机器学习评价语境中对应 "分组 / 分箱" 操作）
3.3 专家层的数量、规模与频率的缩放调控
除稠密 Transformer 模型已有的超参数外，另有几项关键超参数会主导稀疏专家模型的缩放过程，具体包括：1）专家网络的数量；2）单个专家网络的规模；3）专家层的设置频率。这些参数的选择，会对模型在上游任务与下游任务 中的缩放效果产生显著影响。（govern the scale of 译为主导...... 的缩放过程，have significant implications to 译为会对...... 产生显著影响）
早期诸多研究采用的方案是，在每个网络层中配置数千个规模相对较小的专家网络 ，这种架构在预训练与翻译任务中均取得了优异的性能表现（沙泽尔等人，2017；列皮欣等人，2020；费杜斯等人，2021）。然而，当面临域偏移场景 时，或是在不同任务分布上进行微调时，稀疏模型的性能会出现显著衰减（阿特克塞等人，2021；费杜斯等人，2021）。目前在少样本推理任务上表现业界领先的稀疏模型（GLaM（杜等人，2021）），以及在微调任务上效果最佳的稀疏模型（ST-MoE（佐夫等人，2022）），均仅采用最多 64 个规模更大的专家网络 ------ 这种设计实现了计算量与参数量之间更优的平衡。由于专家网络的维度有所提升，这类模型需要在加速器上采用特定的系统级分片策略 ，才能保障高效运行（杜等人，2021；拉吉班达里等人，2022），（disproportionately reduced 译为显著衰减，domain shift 译为域偏移场景 对应 "训练数据与测试数据分布不一致" 的场景。，system-level sharding strategies 译为系统级分片策略）
接下来，我们总结当前关于专家层设置频率的通用方案 。稀疏模型的构建通常以稠密模型为基础，然后按固定间隔 或经验性策略 ，在稠密模型中插入或替换稀疏专家层。例如，拉吉班达里等人（2022）将更多稀疏层部署在网络的靠近输出端的层 附近。在 Transformer 架构中，最常用的做法是替换每隔一个的前馈网络层（FFN） （列皮欣等人，2020；杜等人，2021；阿特克塞等人，2021；拉吉班达里等人，2022），即专家层的设置频率为 0.5。不过，研究中也采用过其他频率，例如佐夫等人（2022）采用的每四层设置一次 （频率 0.25），以及费杜斯等人（2021）采用的每层均设置 （频率 1.0）。最终，克拉克等人（2022）推荐采用 0.5--1.0 的设置频率区间 。（recap the current conventions 译为总结当前关于...... 的通用方案，a frequency of 0.5-1.0 is recommended 译为推荐采用 0.5--1.0 的设置频率区间）
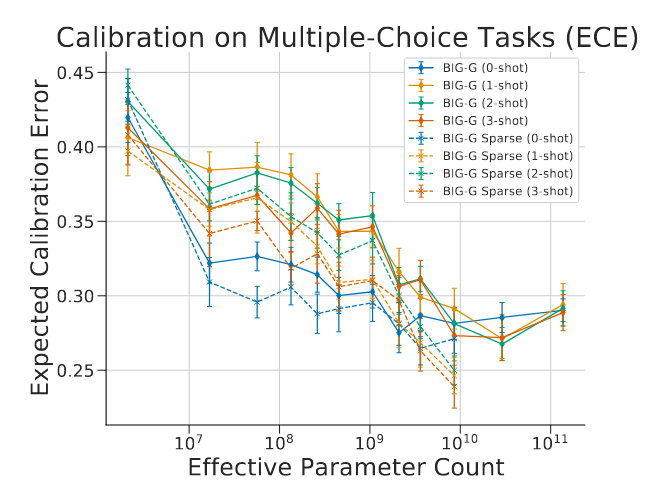
图 5：稀疏模型的校准性能 对于稠密模型与稀疏模型而言，期望校准误差（ECE） 均会随模型规模的扩大而降低。然而，稀疏模型的校准性能表现显著更优，其校准水平大致与规模大 10 倍的稠密模型 相当。本图改编自斯里瓦斯塔瓦等人（2022）的研究成果。（is reproduced from 译为改编自，）
归根结底，最优超参数 的选择取决于具体的应用场景与硬件系统规格。此前的研究表明，采用大量专家网络 的模型在预训练与翻译任务中均取得了出色的效果（沙泽尔等人，2017；列皮欣等人，2020）；而在模型迁移任务中表现最佳的模型，则采用了数量更少、规模更大的专家网络 （杜等人，2021；佐夫等人，2022；穆斯塔法等人，2022）。此外，这类参数的选择还高度依赖硬件配置 。由于实现动态路由需要额外的全对全（all2all）通信开销，对于互联传输速度较慢的网络而言，若要在特定性能指标下追求训练时长最优，设置更少的专家层会是更合适的方案。对分布式系统的计算、内存与通信特性进行仿真模拟，将能大幅帮助相关从业者更高效地确定最优参数配置，无需再耗费大量成本进行反复试错。（on a time-basis to a certain quality 译为在特定性能指标下追求训练时长最优，costly trail-and-error launches 译为耗费大量成本进行反复试错）
需要说明的是，本研究的分析内容与各项权衡取舍，均是针对 **"专家层化" 方案 ** 展开的（艾根等人，2013）。与之不同的是，专家模型的分支 - 训练 - 合并（BTM）方案 （李等人，2022）具有 **"易并行化"** 的特性 ------ 该方案中，每个专家都是一个完整的语言模型，可独立、异步地进行训练，无需承担高昂的通信成本。因此，该方案以及其他同类方案，其缩放特性会随专家数量的变化呈现出截然不同的规律 。（embarrassingly parallel 采用领域通用译法 **"易并行化"**，following-suit 译为同类方案，fully formed language model 译为完整的语言模型）
4 路由算法
稀疏专家模型的核心挑战在于如何为每个输入样本选择合适的专家网络 ，这一问题直接决定了模型的性能上限。该领域已开展了大量深入研究，其中不乏一些反直觉的方法，例如采用固定且无需学习的路由模式（罗勒等人，2021）。通常来说，朴素路由策略的决策过程是不可微的 ，因为它需要对 "选择哪些专家网络" 做出离散化的判定。专家选择问题可以被重新建模为多臂老虎机问题 ，已有多项研究采用强化学习的方法来学习最优的选择策略（本吉奥等人，2016；罗森鲍姆等人，2017、2019；克拉克等人，2022）。沙泽尔等人（2017）提出了一种可微的启发式路由方法 ，绕开了强化学习所面临的技术难题。该方法并非直接将样本分配给选定的专家网络并执行计算，而是将专家网络的计算输出，与被选中的概率进行加权融合（公式 2）。由于专家被选中的概率是一个可微变量，这一设计可以为路由模块提供有效的梯度信息以完成训练。与 "可能仅选择单个专家网络" 的老虎机方法不同，沙泽尔等人（2017）提出了一个重要假设：路由策略需要选择排名前 k 的专家网络（k>1） 。其核心思路在于，让两个或多个专家网络处理同一个样本，能够使模型在训练过程中对比不同专家的表现，进而优化整体的相对性能。列皮欣等人（2020）随后将这一路由算法适配到 Transformer 架构中，取得了当时业界领先的机器翻译效果。但费杜斯等人（2021）的研究表明，仅选择排名第一的专家网络（top-1 路由）也能实现具有竞争力的性能 ，这一结论也得到了后续研究的验证（克拉克等人，2022）。（naive routing decision 译为朴素路由策略，non-differentiable 译为不可微的，Bandit problem 译为多臂老虎机问题，differentiable heuristic 译为可微的启发式路由方法，achieve competitive results 译为实现具有竞争力的性能）
4.1 路由算法分类体系
理解各类路由算法的一种有效方式，是对路由得分矩阵 （即图 2 所示的路由模块输出得分）展开分析。我们以一个自然语言稀疏专家模型为例进行说明。图 6 展示了三个 Token（列）分配至五个专家网络（行）时得到的未归一化路由得分。矩阵中的每个数值，均由 Token 嵌入向量与专家嵌入向量（基于路由模块权重生成）的点积计算得出。
得到得分矩阵后，确定 "哪些 Token 分配给哪些专家网络" 的方法有多种。我们重点介绍三类常用的分配策略：
- 以 Token 为中心：每个 Token 选择排名前 k 的专家网络；
- 以专家网络为中心：每个专家网络选择排名前 k 的 Token；
- 全局优化策略：从全局层面确定 Token 与专家网络的分配关系（不采用贪心策略）。
这一分类体系还进一步启发了许多尚未被探索的路由算法 。例如，可设计一种算法，同时对路由得分矩阵进行横向与纵向的考量，但又不会产生全局优化策略的计算开销 ------ 具体流程为：先让每个 Token 自主选择期望分配的专家网络，再让各个专家网络基于 Token 的选择结果，筛选出自身需要处理的 Token。（taxonomy 译为分类体系，benefits by looking both horizontally and vertically 译为同时对路由得分矩阵进行横向与纵向的考量，without incurring the cost 译为不会产生...... 计算开销）
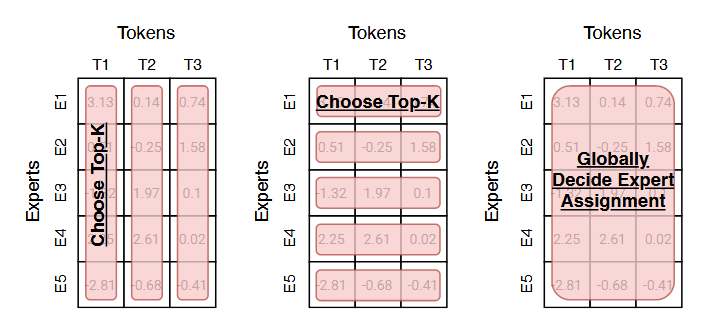
图 6：三类常用路由算法 我们借助一个专家数 ×Token 数 的激活矩阵，对这三种方法进行阐释，该矩阵通过图 2 所述流程得到。左图：沿专家维度选取排名前 k 的对象 ，此类方法包含标准的 top-k 路由算法（沙泽尔等人，2017；列皮欣等人，2020）。中图：沿 Token 维度选取排名前 k 的对象 ，周等人（2022）提出的路由算法即属于此类。右图：全局决策专家分配策略，例如基础层（BASE layer）相关算法（刘易斯等人，2021；克拉克等人，2022）。
每个 Token 选择排名前 k 的专家网络 。这类路由算法的核心机制是，让每个 Token 自主挑选排名前 k 的专家网络并完成分配。这正是沙泽尔等人（2017）提出的原始 top-2 路由范式 ，列皮欣等人（2020）也采用了该方法，并在机器翻译任务上取得了业界领先的性能表现 。费杜斯等人（2021）与拉吉班达里等人（2022）成功应用了top-1 路由策略 。克拉克等人（2022）提出了一种基于强化学习的路由算法，同样采用了 top-1 的选择逻辑。但与传统方法不同的是，该算法并未将专家网络的计算输出按路由概率进行加权缩放，而是采用了REINFORCE 算法 （威廉姆斯，1992），并将预测 Token 的负交叉熵作为奖励信号。图 7 展示了 top-1、top-2 以及基于强化学习的这三种路由算法。
杨等人（2021）提出了一种top-1 路由的扩展方案 ：通过专家原型划分方法将专家网络划分为不同组别，随后在每个组别内分别执行 top-1 路由流程。聂等人（2021）则设计了一种渐进式路由策略，初始阶段采用软门控机制 ------ 让所有专家网络均参与训练（等同于稠密模型的训练模式），再逐步过渡到标准的 top-1 路由算法。这种名为DTS-Gate 的方法，在 OpenWebText 预训练任务上的表现优于 Switch Transformer 模型（费杜斯等人，2021）。杜阿等人（2021）提出了一种类似的思路：先训练一个稠密模型，让每个输入样本流经所有专家网络，再将其适配为稀疏模型。哈齐梅赫等人（2021）提出了DSelect-k 算法 ，这是 top-k 路由算法的一种平滑改进版本，性能优于标准的 top-k 路由方法。拉吉班达里等人（2022）设计了PR MoE 模型，该模型虽采用 top-2 路由的框架，但每个输入样本只会被发送至一个共享稠密层与一个自主选定的专家网络（而非两个专家网络）。
杨等人（2021）提出了一种top-1 路由的扩展方案 ：通过专家原型划分方法将专家网络划分为不同组别，随后在每个组别内分别执行 top-1 路由流程。聂等人（2021）则设计了一种渐进式路由策略，初始阶段采用软门控机制 ------ 让所有专家网络均参与训练（等同于稠密模型的训练模式），再逐步过渡到标准的 top-1 路由算法。这种名为DTS-Gate 的方法，在 OpenWebText 预训练任务上的表现优于 Switch Transformer 模型（费杜斯等人，2021）。杜阿等人（2021）提出了一种类似的思路：先训练一个稠密模型，让每个输入样本流经所有专家网络，再将其适配为稀疏模型。哈齐梅赫等人（2021）提出了DSelect-k 算法 ，这是 top-k 路由算法的一种平滑改进版本，性能优于标准的 top-k 路由方法。拉吉班达里等人（2022）设计了PR MoE 模型 ，该模型虽采用 top-2 路由的框架，但每个输入样本只会被发送至一个共享稠密层与一个自主选定的专家网络（而非两个专家网络）。（expert prototyping 译为专家原型划分方法，anneals down to 译为逐步过渡到，）
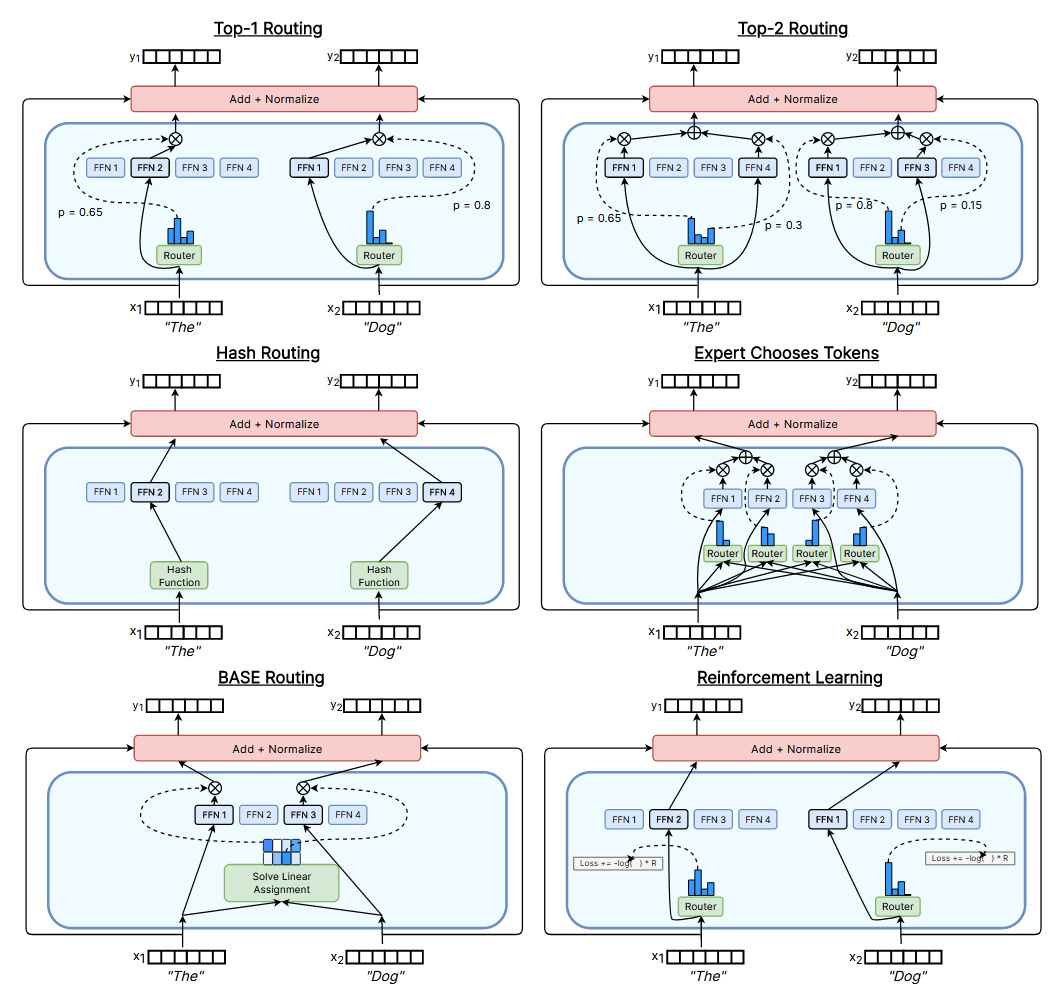
图 7：六种不同路由算法的可视化展示 每张示意图均以一个配备 **4 个专家网络（前馈网络）** 的 Transformer 稀疏专家模型为对象，展示了模型对两个 Token（"The" 与 "Dog"）的路由分配过程。（routing two tokens 译为对两个 Token...... 的路由分配过程）
里克尔梅等人（2021）针对视觉 Transformer（ViT）图像分类模型，提出了一种基于 top-k 路由的改进方案，名为批次优先级路由（Batch Prioritized Routing，BPR） 。混合专家（MoE）模型会为每个专家网络设置固定的批次容量，若容量不足，就会出现 Token "溢出" 的情况。一旦发生 Token 溢出，该专家网络将不会对溢出的 Token 执行任何计算操作。在传统的 top-k 路由算法中，当专家网络发生溢出时，优先级判定的规则是保留句子或批次中较早分配的 Token ，舍弃后分配的 Token。而批次优先级路由（BPR）则改为优先保留路由得分更高的输入 Token 。这种设计对视觉 Transformer（ViT）模型尤为适用，因为这类模型的输入不具备自回归特性，所有输入数据均可被模型同时处理。反观自然语言处理任务，输入文本通常遵循从左到右的顺序结构，这一特性在理论上可能导致模型在训练过程中出现 "投机取巧" 的行为。佐夫等人（2022）的研究证实，批次优先级路由（BPR）对混合专家（MoE）语言模型同样具有优化效果。金等人（2021）则提出了另一种优化思路：对序列中 Token 的优先级进行随机化处理，以此确保路由决策不会偏向于句子中靠前出现的 Token。（Batch Prioritized Routing (BPR) 译为批次优先级路由（BPR），fixed batch sizes per expert 译为为每个专家网络设置固定的批次容量，no autoregressive nature to the inputs 译为输入不具备自回归特性，allow the model to cheat during training 译为导致模型在训练过程中出现 "投机取巧" 的行为，）
静态路由
大多数路由算法会在训练过程中动态学习路由决策 ，但路由决策也可以在训练开始前静态确定 。动态路由算法通常基于网络内部的输入表征进行运算，因此其路由决策会纳入当前 Token 与模型的历史输入信息（通常借助自注意力层实现）。多数路由算法都属于动态路由范畴，但静态路由算法也有一个典型案例，即罗勒等人（2021）提出的哈希层（Hash Layers） 。该研究表明，通过对输入 Token 进行哈希运算来实现随机固定路由 ，其性能可与通过学习得到的路由方法相媲美。这种方法在训练前便选定哈希函数，借助哈希函数实现 Token 批次的均衡分配，进而达成负载均衡 的目标。哈希层的结构示意图详见图 7。（Static routing / Dynamic routing 译为静态路由 / 动态路由，internal input representations 译为内部输入表征，random fixed routing by hashing the input token 译为通过对输入 Token 进行哈希运算来实现随机固定路由）
每个专家网络选择排名前 k 的 Token。
周等人（2022）摒弃了 "由每个 Token 自主选择分配至哪些专家网络" 的传统思路，转而采用反向设计 ------ 让每个专家网络自主挑选需要接收的 Token。这种方式省去了 训练过程中额外添加负载均衡辅助损失函数的步骤，也无需借助线性分配算法。在该机制下，每个专家网络分配到的 Token 数量始终保持一致，但可能出现部分 Token 未被任何专家网络选中，或是部分 Token 被所有专家网络接收的情况。从实验结果来看，该算法表现优异，且具备自适应计算的特性 ------ 模型能够隐性地为特定 Token 分配更多的计算资源。（flips this 译为采用反向设计，adaptive computation interpretation 译为自适应计算的特性，结合上下文将 "interpretation" 转化为 "特性"）
全局确定各专家网络应分配的 Token。
基础层（BASE layers）（刘易斯等人，2021）将 Token 路由问题视为线性分配问题 。该方法的目标是，为每个专家网络分配固定数量的 Token，同时最大化路由得分矩阵的总分。由于同一处理器上的 Token 均来自相同句子，彼此关联性较强，因此在各设备上局部求解线性分配问题之前，需要对 Token 进行随机打乱重排 。这一打乱操作会在正向传播与反向传播过程中，额外引入两种通信原语（全对全通信）。克拉克等人（2022）提出了基础层的改进版本（S-BASE），该版本采用最优传输的公式框架进行建模。
其他路由算法
部分路由算法无法被清晰地归入上述三类。左等人（2021）提出了THOR 算法 ，该算法在训练与推理阶段会为每个输入随机选取两个专家网络，实验结果显示，其性能相较标准混合专家（MoE）模型提升了 2 个 BLEU 值。古鲁兰甘等人（2021）提出了DEMix 算法 ，该算法针对性地为不同预训练领域（如法律、医学等）配置了专属的专家网络，在执行路由时，可通过对输入数据进行领域匹配来选定对应的专家网络。范等人（2021）采用了显式的语言专属子层结构 ，输入 Token 可根据自身所属的语言类型，被确定性地分配至对应子层，从而无需依赖动态路由算法。马等人（2018）提出了一种多门控路由算法 ，该算法为每个任务都配置了专属的门控函数。（do not neatly fall into 译为无法被清晰地归入，explicitly has different experts for different pre-training domains 译为针对性地为不同预训练领域配置了专属的专家网络，deterministically routed 译为被确定性地分配）
4.2 负载均衡
大多数路由算法会在训练过程中添加一个辅助损失函数来实现负载均衡，以此促使分配给各个专家网络的 Token 数量趋于均等（沙泽尔等人，2017）。部分路由算法则通过自身的架构设计来解决负载均衡问题：
- 基础层（BASE Layers）（刘易斯等人，2021）将路由问题建模为一个线性分配问题，并在问题定义中强制要求每个专家网络分配到的 Token 数量完全相同。
- 克拉克等人（2022）提出的 S-BASE 算法遵循了类似的设计思路，但采用最优传输理论来求解这一分配问题。
- 聂等人（2021）则采用了渐进式的训练策略：先训练一个所有 Token 都会被发送至每个专家网络的混合专家模型，再逐步将网络适配为 top-1 路由模式。该算法无需额外设计负载均衡机制，因为模型会在训练过程中自然地学习到专家网络表征的专业化分工。
5 跨领域稀疏专家模型
稀疏专家模型与混合专家（MoE）模型发源于自然语言处理（NLP）领域并在该领域得到推广。该领域是大型模型的天然适配场景 ------ 一方面，万亿级别的海量 Token 数据易于获取；另一方面，下一词预测与掩码语言建模 等效果优异的自监督学习算法已十分成熟。然而，这类模型的影响力正迅速拓展至其他领域，包括计算机视觉、语音识别 以及多模态应用 等方向。自然语言处理领域相关技术能够快速向其他领域迁移，得益于 Transformer 架构在各类领域与模态任务中均被迅速采纳。相关应用案例包括图像分类（多索维茨基等人，2020）、目标检测（卡里翁等人，2020）、推荐系统（陈等人，2019）、语音识别（董等人，2018；中谷等人，2019；古拉蒂等人，2020）。（Sparse expert and MoE models 译为稀疏专家模型与混合专家（MoE）模型，introduced and popularized 译为发源于...... 并在该领域得到推广）
在不同领域中，稀疏架构与算法的核心框架基本保持一致，差异之处在于分配给专家网络的输入数据有所不同 。表 1 列出了稀疏层在多个不同领域下对应的各类输入形式。（different sparse layer inputs 译为稀疏层对应的各类输入形式）
表 1：不同领域下稀疏模型的输入数据这些输入数据既用于判定样本应被分配至哪一个专家网络，同时也是混合专家（MoE）层执行计算的处理对象。
5.1 自然语言处理
最初，沙泽尔等人（2017）将混合专家层引入长短期记忆（LSTM）语言建模 与机器翻译 任务中。当时，这些混合专家层是嵌入在 LSTM 模型的标准网络层之间的。后续的相关研究则均基于Transformer 架构 展开，并且通常会直接使用专家层来替代原有的稠密层。（Follow up works 译为后续的相关研究）
列皮欣等人（2020）首次将混合专家层（MoE）引入 Transformer 架构，并在机器翻译的应用场景下对其展开研究。当他们将每个专家层的专家数量扩展至 2048 个时，模型在 100 种不同语言的翻译任务中均取得了业界领先的性能表现 。费杜斯等人（2021）随后研发出一个拥有 1.6 万亿参数的稀疏语言模型，该模型在预训练任务上达到了当时的最优效果。他们还尝试在自注意力层中，利用稀疏层来生成查询（q）、键（k）和值（v）的激活值，但发现这种技术方案的稳定性相对较差。李 - 索普与安斯利（2022）提出了 ** 快速稀疏混合器（Fast Sparse Mixer）** 模型，这是一个纯编码器模型，与 BERT 模型（德夫林等人，2018）相比，其训练速度提升了 89%，推理速度提升了 98%。
近年来，自然语言处理（NLP）领域涌现出大量围绕混合专家（MoE）模型展开的各类研究。例如，此前该领域的混合专家架构均在单词或字节对层面 执行路由操作。而库杜贡塔等人（2021）则提出了一种新的混合专家架构，将路由粒度提升至任务或句子层面 ，这一设计能有效提升模型的推理效率与部署性能。该研究是在机器翻译的应用场景下开展的 ------ 具体的路由策略为，根据句子的目标翻译语言来完成分配。
新的研究成果已成功刷新小样本推理与微调基准的业界最优水平 。杜等人（2021）训练了一个仅解码器结构的混合专家语言模型 ，不仅取得了小样本任务的最优结果，其训练所需的计算量仅为 GPT-3 的三分之一。佐夫等人（2022）提出了ST-MoE------ 一种稀疏编解码器模型，该模型在多项推理与生成任务（包括 SuperGLUE、ARC 简单 / 挑战集、XSum、CNN-GM、Web-QA、ANLI 以及 Winogrande）中均达到了业界领先水平。在 SuperGLUE 任务的微调环节中，ST-MoE 的性能超越了 PaLM-540B（乔德赫里等人，2022），而其预训练浮点运算量（FLOPs）仅为后者的约 1/20，推理阶段的浮点运算量更是降至后者的约 1/40。
5.2 计算机视觉
得益于 Transformer 架构的通用性（例如视觉 TransformerViT，多索维茨基等人，2020），将混合专家（MoE）架构的相关改进方案跨领域应用的实践已取得丰硕成果。里克尔梅等人（2021）通过在视觉 Transformer（ViT）架构中嵌入混合专家层，构建了一款视觉领域的混合专家模型，即视觉混合专家模型（V-MoE）。该模型被应用于图像分类任务，在性能与此前业界领先的模型持平的前提下，仅需耗费一半的推理计算资源。娄等人（2021）基于多层感知机混合器（MLP-Mixer）架构（托尔斯季欣等人，2021），提出了一款面向图像分类任务的稀疏混合专家多层感知机模型。相较于对应的稠密模型版本，该混合专家改进版本在 ImageNet 与 CIFAR 数据集上均取得了更优的图像分类性能。
吴等人（2022）通过其提出的残差混合专家层 ，提升了混合专家（MoE）模型的训练效率。该架构在图像分割 与目标检测 任务上，相较标准混合专家模型，训练成本降低了 30%，同时保持了相当的性能水准。黄等人（2022）为混合专家层设计了一套高效的框架与自适应并行策略 。为验证该系统的性能，他们将混合专家层嵌入 Swin Transformer V2 架构（刘等人，2022），并应用于图像分类与目标检测任务。相较于此前的混合专家模型实现方案，该改进版本的训练与推理速度均提升了 1.5 至 2 倍。阿尔俊迪等人（2017）将专家模型应用于持续学习 场景，在训练过程中逐步新增专家网络，最终在图像分类与视频预测任务上取得了性能提升。卡恰等人（2021）针对基于 CIFAR 与 MNIST 数据集的图像分类模型，提出了在训练过程中动态增加专家数量 的策略。拉马钱德兰与勒（2018）探究了模型深度 与架构多样性 对稀疏专家模型性能的影响，并据此在图像识别任务上实现了性能增益。基尔希等人（2018）提出了一种基于输入数据的端到端条件计算算法，该算法在图像分类任务中展现出优异的性能表现。
5.3 语音识别
SpeechMoE 模型（尤等人，2021）将混合专家（MoE）Transformer 模型应用于语音识别任务，在四个数据集上均显著降低了字符错误率。该研究采用了创新的辅助损失函数以增强模型稀疏性，并提出了一种全新的路由架构。SpeechMoE2 模型（尤等人，2022）进一步优化了 SpeechMoE 的性能表现，其核心改进是设计了一种新的路由算法 ------ 该算法在路由决策过程中融入了全新的辅助信息。熊谷等人（2021）则在两种不同的 Transformer 语音架构（序列到序列架构与变换器架构）中引入混合专家层，以此实现了多语言语音识别任务的性能提升。
5.4 多模态与多任务
穆斯塔法等人（2022）通过训练一款混合专家模型（LIMoE）开展多模态学习研究，该模型以图像与文本数据作为输入，采用了与 CLIP 模型（拉德福德等人，2021）类似的对比损失函数完成训练。混合专家层能够将图像块与单词 Token 同时分配至可用的专家网络。在采用可比训练策略的情况下，该模型性能优于 CLIP；当进一步扩大模型规模后，其性能可与业界领先方法持平。
6 稀疏模型与稠密模型的适用场景选择
一个常见的问题是：在给定固定计算资源或浮点运算次数预算（例如，100 块图形处理器运行 20 小时）的情况下，应该训练哪种类型的模型才能实现最优性能？诸多先前的研究表明，在这类场景下，稀疏模型的表现要优于稠密模型（沙泽尔等人，2017；列皮欣等人，2020；费杜斯等人，2021；杜等人，2021；阿特克塞等人，2021；刘易斯等人，2021）。既然稀疏模型已经取得了如此多亮眼的业界领先成果，那么在哪些情况下，我们反而不应该优先选择稀疏模型，而是选择稠密模型呢？（why should you ever not use... 译为那么在哪些情况下，我们反而不应该......）
概括来讲，当你拥有大量加速器（如图形处理器 / 张量处理器）以承载稀疏化所带来的全部额外参数时，稀疏化的优势便能得以发挥。模型的训练通常采用数据并行 的方式，即不同的计算设备会分配到不同的训练 / 推理数据分片。此时，原本用于处理这些数据分片的设备，便可转而承载更多的模型参数。因此，稀疏模型适用于以下两种场景：一是采用数据并行的方式进行训练；二是模型在部署时需具备高吞吐量 ------ 也就是在多台能够承载全部模型参数的设备上完成训练与部署任务。（throughput ：译为吞吐量）
采用稀疏化技术时，还需审慎考量模型在下游任务中的实际应用方式。若用于预训练模型的计算设备数量充足，但用于微调或部署的设备数量却明显不足，那么稀疏化的程度（例如专家网络的数量）就应当根据下游应用场景的可用内存容量进行适配调整。这也是相关研究文献中一项常见的实际设计考量因素。（fine-tuning ：译为微调，serving ：结合技术语境译为部署）
从单位参数的性能表现 来看，稀疏模型的表现往往会逊色于稠密模型。假设所有参数均存储在加速器内存中，这就类似于一个场景：我们需要找出能适配特定硬件规模（例如 4 块图形处理器）的最优模型，在这种情况下，稀疏模型同样会是比稠密模型更差的选择。正如前文所述，当你具备多设备并行训练或部署的条件 ，足以承载由专家网络带来的额外模型参数时，稀疏模型才会是理想之选。（on a per parameter basis ：译为从单位参数的性能表现来看，host the additional model parameters ：译为承载额外的模型参数）
不过，在内存受限的场景下，稀疏模型并非完全没有用武之地。费杜斯等人（2021）的研究表明，稀疏模型即便仅设置两个专家网络 也能实现良好性能，而这种配置所需的额外内存相当有限。新的研究成果还实现了一种技术方案：通过在中央处理器（CPU）与图形处理器（GPU）/ 张量处理器（TPU）之间动态交换模型内存数据，来解决硬件内存不足的问题（详见 2.2 节）。此外，关于降低稀疏模型内存占用的其他方法，将在 7.3 节展开讨论。
7 稀疏模型训练优化
稀疏模型的训练动态往往与稠密模型有所不同，并且能够从特定的训练与微调方法中获益。
7.1 训练不稳定性
有大量研究表明，稀疏模型的训练过程往往更容易出现不稳定性，具体表现为损失函数发散并持续上升（列皮欣等人，2020；费杜斯等人，2021；佐夫等人，2022；穆斯塔法等人，2022）。这种不稳定性在模型规模扩大时，出现的概率会更高。列皮欣等人（2020）在训练参数量达万亿级别的模型时，使用 bfloat16 精度存储激活值，便遭遇了训练不稳定的问题。费杜斯等人（2021）研发的计算开销最高的 Switch-XXL 模型，同样出现了训练不稳定的现象。佐夫等人（2022）发现其大尺寸模型的训练过程存在不稳定性，在多语言任务场景下，该问题尤为突出。穆斯塔法等人（2022）则观察到，在同时对图像与文本数据进行多模态训练时，模型的不稳定性会有所加剧。（loss diverges and increases ：译为损失函数发散并持续上升，）
学术界已开展大量研究，旨在改善稀疏模型的训练动态。列皮欣等人（2020）发现，采用更高精度（32 位浮点数）对模型进行训练，能够解决大模型的训练不稳定问题，但这种方法会带来更高的内存占用与更慢的训练速度。费杜斯等人（2021）提出，可通过采用更小的权重初始化尺度，并仅将路由网络的特定子集转换为更高精度，来提升模型的训练稳定性。杜等人（2021）则采取了如下策略：在训练过程中，跳过梯度中包含非数值（NaN）或无穷值（Inf）的数据批次；当训练出现发散时，从模型的早期检查点重新开始训练。阿特克塞等人（2021）针对专家层批量大小缩减的问题，提出了一种更优的专家层初始化方案。由于每个专家网络对应的批量大小为B/E，作者建议将专家层的梯度按1/E的比例进行缩放。佐夫等人（2022）引入了路由器 z 损失 ，该方法可同时改善模型的训练不稳定性与最终性能。这一辅助损失的设计目标是，通过促使输入至路由函数的对数几率（logits）在训练全程保持较小数值，来降低浮点运算的舍入误差。穆斯塔法等人（2022）对多种解决模型不稳定性的技术进行了全面研究，并采用了一套组合方案，其中包含路由器 z 损失与两种创新的熵损失函数。（NaNs/Infs：非数值（Not a Number）与无穷值（Infinity））
7.2 向新数据分布的迁移
多篇研究论文指出，尤其是在大模型规模下，将混合专家（MoE）模型迁移至新领域（即微调过程）时，其性能表现会落后于对应的稠密模型。费杜斯等人（2021）、纳兰等人（2021）对比了稠密模型与稀疏模型的预训练困惑度和微调性能。他们发现，在预训练困惑度相同的前提下，稀疏模型在推理类任务上的微调效果较差，但在知识密集型任务上的表现更优。此外，阿特克塞等人（2021）观察到，除了域外语言建模性能表现不佳之外，稀疏模型在多项任务（包括 HellaSwag、PIQA 和 Winogrande）的微调中，效果均不如稠密模型。（pre-training perplexity ：译为预训练困惑度，）
针对微调存在的问题，目前已有多种解决方案被提出。第一种方案是通过提升浮点运算量而非增强稀疏性 来对模型进行扩展（例如，减少专家网络的数量，但增大单个专家网络的规模）。费杜斯等人（2021）曾训练过一个配备 2048 个专家网络、参数量达 1.6 万亿的模型，但其浮点运算量仅与 20 亿参数量的稠密模型相当。与之相反，在微调任务中表现最优的模型仅设置了 128 个专家网络，浮点运算量却达到了 110 亿参数量稠密模型的水平。由此可见，在模型扩展时，以降低稀疏程度为代价换取更高的浮点运算量 ，是一种能够直接提升微调性能的简便方法。佐夫等人（2022）发现，稠密模型与稀疏模型对应的最优微调超参数 （例如学习率与批量大小）可能存在显著差异。若将适用于稠密模型的最优超参数直接套用在稀疏模型上，稀疏模型在预训练阶段积累的性能优势可能会被完全抵消 ------ 因此，专门针对稀疏模型开展独立的超参数研究十分必要。（scale models ：译为对模型进行扩展 ，指通过调整参数量、计算量等指标提升模型容量，trading off...for... ：译为以...... 为代价换取......，mask any of the sparsity pre-training improvements ：译为完全抵消稀疏模型在预训练阶段积累的性能优势）
7.3 推理阶段
从设计原理来看，稀疏专家模型的参数量远多于对应的稠密模型。尽管其计算量仍维持在相对较低的水平，但内存占用量 会成为一项负担。因此，已有部分研究聚焦于减少模型在推理阶段所需的参数量，以此降低部署阶段的需求门槛。库杜贡塔等人（2021）在机器翻译任务中，将路由操作的粒度从单词或 Token 级别提升至任务级别。这种设计只需加载当前任务所需的权重子集，因此能够实现更高效的推理。金等人（2021）在推理阶段对专家网络进行剪枝，以此降低模型的内存占用。该研究采用了两种剪枝方法：一是随机选取部分专家网络；二是筛选出推理阶段利用率最高的专家网络。费杜斯等人（2021）针对语言建模与微调任务，提出了将大型稀疏模型知识蒸馏 为小型稠密模型的方案。拉杰班达里等人（2022）则探索了面向语言建模任务的稀疏模型蒸馏方法，具体手段为减少网络中专家层的深度。同时，该团队还在 DeepSpeed 框架中实现了一个经过优化的混合专家（MoE）模型版本，与现有框架相比，其推理延迟缩短了 7.3 倍。（inference-time ：译为推理阶段）
8 可解释性
稀疏专家模型的结构天然更适合开展可解释性研究，原因在于每个输入样本仅由模型权重中一个可识别的离散子集（即被选中的专家网络）负责处理 。因此，研究人员无需再面对解读多达万亿级浮点参数的艰巨任务，只需读取一组规模较小的离散整数 ------ 这些整数即对应着输入样本被分配至的专家网络编号。沙泽尔等人（2017）以WMT 2014 英法机器翻译任务 为研究场景，针对其含 2048 个专家网络的混合专家层编码器，开展了专家网络功能特化的初步研究。研究团队识别出了三个具有明显功能偏向的专家网络：第一个专门处理与 "创新" 相关的词汇；第二个负责处理冠词 a ；第三个则会被分配到与 "速度" 相关的同义词输入。（interpretability ：译为可解释性，identifiable, discrete subset ：译为可识别的离散子集）
针对基于 Transformer 的架构，刘易斯等人（2021）开展了更为深入全面的分析。刘易斯等人（2021）设计了一项研究实验：他们追踪记录了专家网络被选中时，出现频率最高的历史输入 Token 。该研究揭示了专家网络在多个维度上的功能特化倾向，包括数量词、数字、所有格、子词片段，以及由相关动词、名词和形容词构成的语义簇，部分研究结果详见表 2。（extensive analyses ：译为深入全面的分析，possessives ：译为所有格，clusters of related verbs, nouns and adjectives ：译为由相关动词、名词和形容词构成的语义簇）
表 2：基础层中基于前文语境的专家网络功能特化 本文重现了刘易斯等人（2021）研究中的部分表格内容，列出了被选中的各专家网络对应的出现频率最高的前五类前文 Token 。该示例体现了专家网络分别在标点符号、连词与冠词、动词、视觉描述、专有名词、计数与数字等维度的功能特化倾向。（preceding context ：译为前文语境，the most frequent preceding top-five tokens ：调整语序译为出现频率最高的前五类前文 Token，conjunctions & articles ：译为连词与冠词，proper names ：译为专有名词）
佐夫等人（2022）训练了一个编解码器结构的 Transformer 模型，并在编码器中发现了类似的功能特化模式，其中包含一些执行浅层处理任务的专家网络，例如专门负责处理冠词（如 a 、the）的专家。表 3 重现了佐夫等人（2022）研究中观察到的部分专家功能特化案例。这些研究进一步发现，专家网络的功能特化还体现在标点符号、数字、专有名词、动词、颜色词，以及预训练任务中所使用的特殊掩码 Token 等维度。
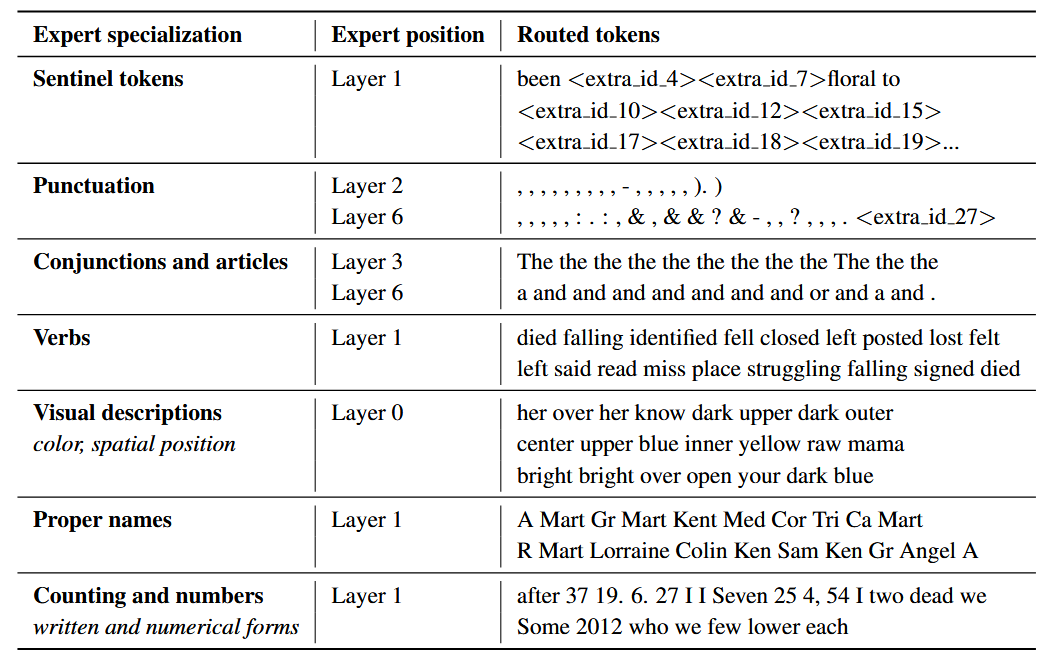
表 3：ST-MoE 模型编码器中专家网络的功能特化本文重现了佐夫等人（2022）的研究表格，展示了专家网络分别在标点符号、连词与冠词、动词、视觉描述、专有名词、计数与数字等维度的功能特化倾向。
但对完整编解码结构的 ST-MoE 模型开展深入分析后发现，编码器中存在更为清晰的专家功能特化迹象，而解码器中则无此表现。这一现象表明，有必要针对专家层的价值定位展开进一步研究。解码器中未发现明显的功能特化，这既可能意味着其特化模式难以识别，也可能说明这类模型的解码器本身并不存在具有实际价值的特化规律。
稀疏专家模型的可解释性研究并非局限于文本领域。一个典型案例是穆斯塔法等人（2022）提出的多模态模型LIMoE ------ 该模型被证实会学习形成具备功能特化的专家网络，这些专家网络分别专注于处理文本数据与视觉数据，涵盖纹理块、植物、眼睛以及文字等多种内容（见图 8）。与文本类模型的特征一致，稀疏专家模型功能特化的复杂程度同样存在显著差异。例如，研究发现文本类专家网络的功能既包含处理冠词 a 这类简单任务，也涉及处理过去式动词这类复杂概念。同理，在多模态模型中，专家网络的特化精细度也存在梯度差异：既可以是基础纹理这类简单视觉概念，也能够是车轮、门把手这类高级视觉对象。（patches of textures 译为纹理块，the sophistication of expert specialization 译为专家网络的特化精细度，）
最后，我们指出这类可解释性研究方法存在的一项显著局限性。这些方法在分析输入至各专家网络的 Token 或图像块时，采用的是一种较为局限的视角。具体而言，单词或图像块的初始嵌入向量，本身就已融入了来自周边数据的上下文信息（Transformer 架构正是通过自注意力机制或编解码注意力机制实现这一点）。因此，这类启发式技术手段，很可能会遗漏掉专家网络更为细微的功能特化模式。要更深入地理解稀疏专家模型，还需要开展更为严谨、全面的可解释性研究工作。阿特克塞等人（2021）与费杜斯等人（2021）发布的稀疏专家模型检查点，为更多研究团队分析并阐释这类模型的训练动态提供了可能。（in a narrow way 译为采用的是一种较为局限的视角，heuristic techniques 译为启发式技术手段，nuanced specialization 译为细微的功能特化模式，sparse expert model checkpoints 译为稀疏专家模型检查点）
9 未来研究方向与结论
尽管稀疏专家模型与混合专家模型的相关研究最早可追溯至 20 世纪 90 年代初，但该领域仍存在诸多亟待解决的问题。在本综述的结尾部分，我们对未来颇具前景的研究方向进行展望，重点聚焦于该领域与两大新兴技术（自适应计算、检索方法）的交叉融合方向，并阐述了我们的总结性思考。（parting thoughts 译为总结性思考）
图 8：LIMoE 模型中视觉专家网络的功能特化本文重现了穆斯塔法等人（2022）研究中的一幅图示，该研究发现，模型中的专家网络会分别特化处理不同类型的视觉内容，包括纹理块（纯色纹理与条纹纹理）、自然物体（植物、手部、眼睛）以及人造物体（车轮、门把手、文字）。
自适应计算
自适应计算的核心思想是：机器学习系统针对不同的输入，可调用不同的计算资源（即计算量或计算类型能够动态适配 ）。稀疏模型则基于一种镜像式的设计思路：模型对每个输入分配的计算量保持一致，但调用的参数集合可能存在差异。不过，这两类技术并非互斥关系；部分路由算法（详见第 4 章）支持将一个 Token 分配给数量不固定的专家网络，以此实现自适应计算（里克尔梅等人，2021；周等人，2022）。未来的模型或将从自适应计算技术的融合中进一步获益 ------ 例如，网络除了可以选择调用哪些专家网络，还能自主决定使用的网络层数（舒斯特等人，2022）。异构专家层同样是适配自适应计算的天然载体。当前多数稀疏模型为了简化设计，并适配现代硬件以提升运行效率，会采用类型与规模完全相同的专家网络。但如果允许专家网络在规模上存在差异（例如网络深度或宽度不同），那么路由决策的结果就会带来不同的计算量消耗。诸如 Pathways（迪恩，2021）之类的新型软件系统，将有助于推动这类异构架构与算法在现代硬件上的高效落地。（adapted on-the-fly ：译为动态适配，mirrored idea ：译为镜像式的设计思路，mutually exclusive ：译为互斥关系，heterogeneous expert layers ：译为异构专家层，facilitate efficient implementations ：译为推动...... 高效落地）
检索方法
检索机制能够让模型动态获取当前上下文或参数中未存储的信息，以此有效拓展模型的容量（坎德瓦尔等人，2019；古等人，2020；博若德等人，2022）。稀疏专家模型与检索模型的目标存在重合之处：二者均致力于提升模型的容量，使其能更高效地存储、检索与应用知识。其中，稀疏专家模型通过参数化的方式 实现这一目标（即依靠专家网络承载更多可学习参数）；而基于检索的系统则采用非参数化的动态检索方式 嵌入信息（具体手段为在语料库上执行最近邻查找）。未来的研究方向中，对这两种方法的权衡分析与融合探索，或将被证实具有重要的实用价值。（Retrieval mechanisms ：译为检索机制，parametrically / non-parametrically ：译为参数化的方式 / 非参数化的方式，trade-offs ：译为权衡分析）
结论
稀疏化技术能够降低模型的训练与推理成本，进而构建出规模庞大的模型，且这类模型的精度表现优于对应的稠密模型。但该领域仍存在诸多悬而未决的问题。例如，我们目前对于专家网络的最优数量与规模如何适配具体任务 这一问题的认知仍十分有限（比如在翻译任务中，应该使用少量大尺寸的专家网络，还是大量小尺寸的专家网络？）。正如诸多研究指出的，要实现优异的域外泛化能力并非易事，相关机制仍需更充分的阐释。此外，当前多数稀疏专家模型的架构多样性相对较低，稀疏层通常以固定间隔的方式嵌入网络。未来的模型或可从非标准化结构 与异构专家架构 中进一步获益。同时，稀疏化的合理粒度也有待明确：现有研究大多聚焦于用专家网络替代前馈网络层这类组件，但已有研究证实，采用完全模块化、相互独立的专家网络具备显著优势（古鲁兰甘等人，2021；李等人，2022）。该领域对稀疏专家模型特性的探索仍在持续推进，例如模型的校准能力已实现大幅提升（斯里瓦斯塔瓦等人，2022）；但仍有诸多特性有待挖掘，包括模型在异步训练模式下的动态表现（雷希特等人，2011），以及模型的记忆能力（卡利尼等人，2020）等。简言之，稀疏专家模型虽带来了大量兼具挑战性的数学、工程与科研难题，但现有解决方案已创造了显著的性能增益，我们坚信该领域未来可期，还将涌现更多技术突破。（granularity of sparsity ：译为稀疏化的粒度，calibration ：译为校准能力，asynchronous training ：译为异步训练）