对于快速排序来说,我最开始学的就是将pivot等于arr[low],然后从high的位置开始,不然就调换,但是这个貌似不稳定是吧 下面是我写的最基础的快速排序的代码
def quick_sort(self,arr,low,high):
if low<high:
pivots=self.partition(arr,low,high)
self.quick_sort(arr,low,pivots-1)
self.quick_sort(arr,pivots+1,high)
return arr
def partition(self,arr,low,high):
pivot=arr[low]
i=low
j=high
while i<j:
while i<j and arr[j]>=pivot:
j-=1
if i<j:
arr[i]=arr[j]
i+=1
while i<j and arr[i]<=pivot:
i+=1
if i<j:
arr[j]=arr[i]
j-=1
arr[i]=pivot
return i#这个得到的i 就是下次进行分开两部分的 要记得返回
solution=Solution()
result=solution.quick_sort([64, 34, 25, 12, 22, 11, 90, 88, 76, 50],0,9)
print(result)
Lomuto 分区 = 用一个指针 i 动态维护"≤ pivot"的区域,遍历过程中把符合条件的元素"交换到左边",最后把 pivot 放到 i+1 位置
这个我看了过程,其实就是i及其左边的元素就是比arr[high]小的元素
就是i=low-1 j=low pivot=arr[high] 然后如果j对应的元素小于pivot那么i+=1,让i位置的元素等于j位置的元素 然后遇到大的就过去,遇到小的就交换,这样的话就可以让小的在左边,大的在右边
def quick_sort1(self,arr,low,high):
if low<high:
pivots=self.partition1(arr,low,high)
self.quick_sort1(arr,low,pivots-1)
self.quick_sort1(arr,pivots+1,high)
return arr
def partition1(self,arr,low,high):
i=low-1
j=low
pivot=arr[high]
for j in range(low,high):
if arr[j]<pivot:
i+=1
temp=arr[i]
arr[i]=arr[j]
arr[j]=temp
arr[high]=arr[i+1]
arr[i+1]=pivot
return i+1
solution=Solution()
result=solution.quick_sort1([64, 34, 25, 12, 22, 11, 90, 88, 76, 50],0,9)
print(result)
这个是这个思想,要注意的就是开始是一个都没,如果这个元素小于,那么就i+=1跟j位置的元素换位置,把大的换到后面,下的换到前面,一直换到j索引=high-1的位置为止,那么作为分割的那个元素就可以和i+1的位置的元素呼唤,因为I+1位置的元素肯定是更大的。这样就开始进行下一轮
然后还有一个h开头的方法,是让pivot=arr[low].然后

意思就是i=low-1 j=high+1
然后i+=1 直到找到比pivot大的定在那里 j找到比Pivot小的定在那里 如果i<j 那么交换 然后继续找 不然的话就返回j 分割点
来写代码:
def quick_sort2(self,arr,low,high):
if low<high:
pivots=self.partition2(arr,low,high)
self.quick_sort2(arr,low,pivots) 是pivots不是 pivots-1
self.quick_sort2(arr,pivots+1,high)
return arr
def partition2(self,arr,low,high):
i=low-1
j=high+1
pivot=arr[low]
while True:
i+=1
while arr[i]<pivot: 是小于不是小于等于而且不加i<j的条件
i+=1
j-=1
while arr[j]>pivot:
j-=1
if i<j:
temp=arr[i]
arr[i]=arr[j]
arr[j]=temp
else:
return j

左边找大于等于 左边遇到小于的才往前走 而且可以自己设计几个例子看while的条件 我开始的适合还写上来i<j的条件

注意是 < 和 >,而不带上等于 带上等于
为什么不需要带上i<j的条件
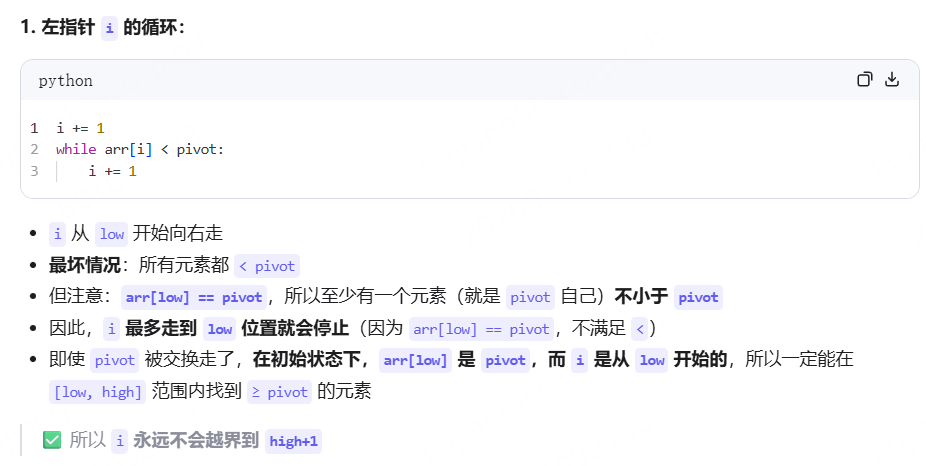
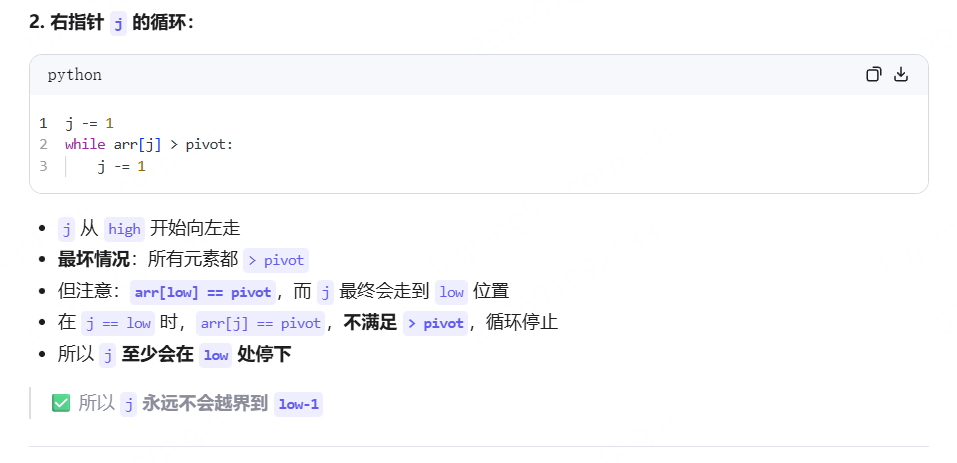

记住得了 关于方法
前面那个是high然后用i使得左边的都是小于的 大的也会被还过去,移动j
这个是交换
欧克先写到这里