给定一个根为 root 的二叉树,每个节点的深度是 该节点到根的最短距离 。
返回包含原始树中所有 最深节点 的 最小子树 。
如果一个节点在 整个树 的任意节点之间具有最大的深度,则该节点是 最深的 。
一个节点的 子树 是该节点加上它的所有后代的集合。
示例 1:
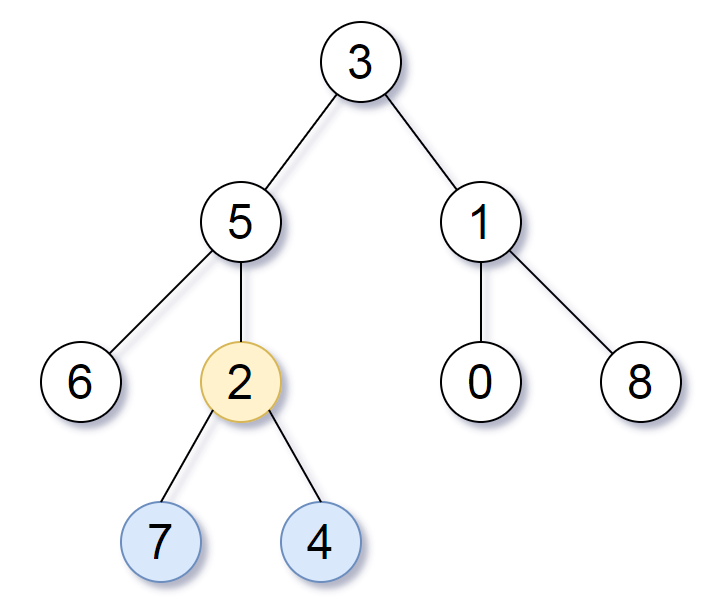
输入:root = [3,5,1,6,2,0,8,null,null,7,4]
输出:[2,7,4]
解释:
我们返回值为 2 的节点,在图中用黄色标记。
在图中用蓝色标记的是树的最深的节点。
注意,节点 5、3 和 2 包含树中最深的节点,但节点 2 的子树最小,因此我们返回它。示例 2:
输入:root = [1]
输出:[1]
解释:根节点是树中最深的节点。示例 3:
输入:root = [0,1,3,null,2]
输出:[2]
解释:树中最深的节点为 2 ,有效子树为节点 2、1 和 0 的子树,但节点 2 的子树最小。提示:
- 树中节点的数量在
[1, 500]范围内。 0 <= Node.val <= 500- 每个节点的值都是 独一无二 的。
分析:先用 BFS 求出每个节点的深度和父节点,记录最大深度和最深的节点,将最深的节点放到一个队列里,当这个队列里的节点数大于 1 时,每次将所有节点出队,并用另一个队列记录所有节点的父节点,直到父节点只有一个时,就是所求的答案。
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
int maxn=1;
map<int,int>depth;
map<int,TreeNode*>father;
vector<vector<TreeNode*>>trace(510);
queue<TreeNode*>que;que.push(root);depth[root->val]=1;trace[1].push_back(root);
while(!que.empty())
{
TreeNode *p=que.front();que.pop();
if(p->left!=NULL)
{
que.push(p->left),father[p->left->val]=p,depth[p->left->val]=depth[p->val]+1;
maxn=fmax(depth[p->left->val],maxn),trace[depth[p->left->val]].push_back(p->left);
}
if(p->right!=NULL)
{
que.push(p->right),father[p->right->val]=p,depth[p->right->val]=depth[p->val]+1;
maxn=fmax(depth[p->right->val],maxn),trace[depth[p->right->val]].push_back(p->right);
}
}
queue<TreeNode*>ans;
for(int i=0;i<trace[maxn].size();++i)
ans.push(trace[maxn][i]);
while(ans.size()>1)
{
queue<TreeNode*>temp;map<TreeNode*,int>mp;
while(!ans.empty())
{
TreeNode *ind=ans.front();ans.pop();
if(mp[father[ind->val]]==0)mp[father[ind->val]]=1,temp.push(father[ind->val]);
}
ans=temp;
}
return ans.front();
}
};